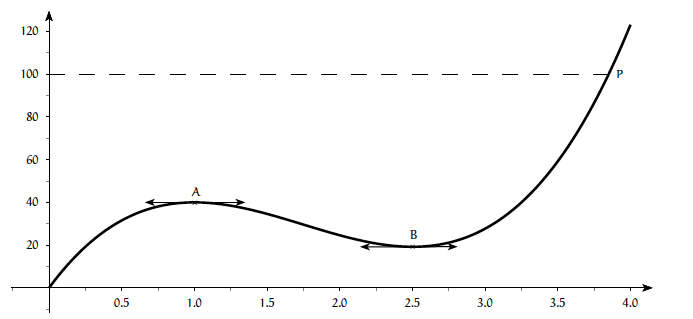
On a dessiné ci-dessous la trajectoire d'un skieur. La tangente au point $A(1; 40)$ est horizontale. Il en est de même pour la tangente au point B d'abscisse 2,5. Un photographe $P$ est situé sur la trajectoire du skieur. Son ordonnée est 100. Le but de l'exercice est de modéliser cette trajectoire par une fonction du troisième degré définie sur $[0; 4]$ que l'on notera $f$. On cherche donc à déterminer $a, b, c$, et $d$ tels que $f(x) = ax^3 + bx^2 + cx + d$. Ensuite, nous chercherons à déterminer l'abscisse du point $P$.
- Montrer que $d = 0$.
- En utilisant les données, écrire un système d'inconnues $a, b$ et $c$.
- Résoudre ce système et en déduire l'expression de $f(x)$.
- Dresser le tableau de variations de $f$ sur $[0; 4]$.
- En déduire que l'équation $f(x) = 100$ admet une solution unique sur l'intervalle $[2, 5; 4]$ puis en donner une valeur approchée au centième à l'aide de la calculatrice.