Baccalauréat S Amérique du Nord 30 mai 2014 - Correction Exercice 2
Correction de l'exercice 2 (6 points)
\[f(x) = 5 \text{e}^{-x} - 3\text{e}^{-2x} + x - 3.\] On note $\mathcal{C}_{f}$ la représentation graphique de la fonction $f$ et $\mathcal{D}$ la droite d'équation $y = x - 3$ dans un repère orthogonal du plan.
Partie A : Positions relatives de $\mathcal{C}_{f}$ et $\mathcal{D}$
Soit $g$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par $g(x) = f(x) - (x - 3)$.
- Justifier que, pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, $g(x) > 0$.
- La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ ont-elles un point commun ? Justifier.
Pour tout réel $x$ de l'intervalle $[0~;~+\infty[$,
$g(x)= 5 \text{e}^{-x} - 3\text{e}^{-2x} = \text{e}^{-x} \left( 5 - 3 \text{e}^{-x} \right) $. Comme $\text{e}^{-x}>0$ (exponentielle), $g(x)$ est du signe de $5 - 3 \text{e}^{-x} $. $5 - 3 \text{e}^{-x} > 0 \Leftrightarrow 5 > 3\text{e}^{-x} \Leftrightarrow \dfrac{5}{3} > \text{e}^{-x} \Leftrightarrow \ln \left( \dfrac{5}{3} \right) >-x \Leftrightarrow \ln \left( \dfrac{3}{5} \right) < x$ ce qui est toujours vrai car $\ln \left( \dfrac{3}{5} \right)<0<x$
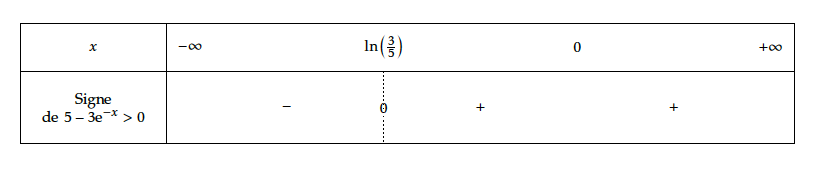
Finalement, pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, $g(x)>0$.
La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ ont un point commun d'abscisse $x$ si et seulement si $ f(x) = x-3$ soit $ g(x) = 0 $ ce qui n'est pas possible car on vient de voir que $g(x) > 0$.
La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ n'ont pas de point commun.
Partie B : Étude de la fonction $g$ On note $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}_{f}$, $N$ le point d'abscisse $x$ de la droite $\mathcal{D}$ et on s'intéresse à l'évolution de la distance $MN$.
- Justifier que, pour tout $x$ de l'intervalle $[0~;~+\infty[$, la distance $MN$ est égale à $g(x)$.
- On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0~;~+\infty[$.
Pour tout $x$ de l'intervalle $[0~;~+\infty[$, calculer $g'(x)$. - Montrer que la fonction $g$ possède un maximum sur l'intervalle $[0~;~+\infty[$ que l'on déterminera.
En donner une interprétation graphique.
Comme $M$ et $N$ ont la même abscisse, pour tout $x$ de l'intervalle $[0~;~+\infty[ $, $MN = \mid f(x) - (x-3) \mid = \mid g(x) \mid = g(x) $ car $g(x) >0$ d'après la première question.
On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0~;~+\infty[$. Si $u$ est dérivable,$\left( \text{e}^{u}\right)' = u' \text{e}^{u} $. La dérivée de $ x \mapsto \text{e}^{-x} $ est donc $ x \mapsto -\text{e}^{-x} $ et celle de $ x\mapsto \text{e}^{-2x} $ est $ x \mapsto -2 \text{e}^{-2x} $.
Pour tout $x$ de l'intervalle $[0~;~+\infty[$, $g'(x) =- 5 \text{e}^{-x} + 2 \times 3 \text{e}^{-2x} = 6\text{e}^{-2x} -5\text{e}^{-x}$.
$g$ étant dérivable sur $[0~;~+\infty[$, on étudie le signe de sa dérivée sur $[0~;~+\infty[$. Pour tout $x$ de l'intervalle $[0~;~+\infty[$, $$\begin{array}{lll} g'(x) \geqslant 0 & \Leftrightarrow 6\text{e}^{-2x} -5\text{e}^{-x} \geqslant 0 & \\ & \Leftrightarrow 6 \text{e}^{-x} -5 \geqslant 0 & \text{on a divisé par } \text{e}^{-x}>0 \\[5pt] & \Leftrightarrow \text{e}^{-x} \geqslant \dfrac{5}{6} & \\[5pt] & \Leftrightarrow - x \geqslant \ln \left( \dfrac{5}{6} \right)& \text{croissance de la fonction } \ln \\[8pt] & \Leftrightarrow x \leqslant \ln \left( \dfrac{6}{5} \right) \\ \end{array}$$ En $ \ln \left( \dfrac{6}{5} \right) $, la dérivée s'annule en changeant de signe $ (+ ; -) $, donc $g\left( \ln \left( \dfrac{6}{5} \right)\right) $ est un maximum pour $g$ sur l'intervalle $[0~;~+\infty[$. $g\left( \ln \left( \dfrac{6}{5} \right)\right) = 5 \times \text{e}^{\frac{5}{6}}-3 \times \left( \text{e}^{\frac{5}{6}}\right)^2 = 5 \times \dfrac{5}{6} - 3 \times \left( \dfrac{5}{6}\right)^2 = \dfrac{75}{36} = \dfrac{25}{12}$.
La distance entre un point de la courbe $\mathcal{C}_{f}$ et le point de même abscisse sur la droite $\mathcal{D}$ est donc maximale lorsque $ x = \ln \left( \dfrac{6}{5} \right) $. Cette distance maximale vaut $ \dfrac{25}{12}$ unités.
Remarque : Comme le repère est orthogonal (a priori pas orthonormé), il s'agit d'unité en ordonnée.)
Partie C : Étude d'une aire
On considère la fonction $\mathcal{A}$ définie sur l'intervalle $[0~;~+\infty[$ par
\[\mathcal{A}(x) = \displaystyle\int_{0}^x [f(t) - (t - 3)]\: \text{d}t.\]
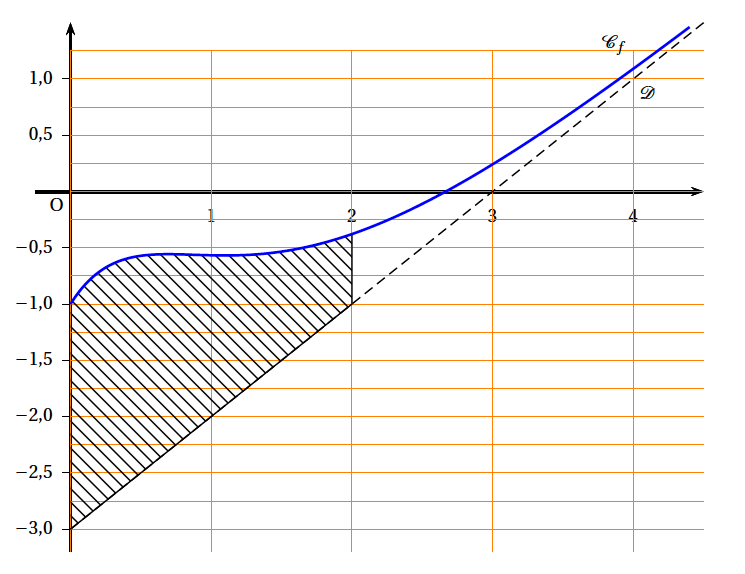
- Hachurer sur le graphique donné en annexe 1 (à rendre avec la copie) le domaine dont l'aire est donnée par $\mathcal{A}(2)$.
- Justifier que la fonction $\mathcal{A}$ est croissante sur l'intervalle $[0~;~+\infty[$.
- Pour tout réel $x$ strictement positif, calculer $\mathcal{A}(x)$.
- Existe-t-il une valeur de $x$ telle que $\mathcal{A}(x) = 2$ ?
La fonction $g$ est continue sur $ [0 ; +\infty [ $ et $ \mathcal{A}(x) = \displaystyle\int_{0}^x g(t)\text{d}t $, la fonction $ \mathcal{A} $ est donc dérivable sur $ [0 ; +\infty [ $ et $ \mathcal{A}' = g >0 $. La fonction $\mathcal{A}$ est donc bien croissante sur l'intervalle $[0~;~+\infty[$
Pour tout réel $x$ strictement positif, $$ \begin{array}{lll} \mathcal{A}(x) & = \displaystyle\int_{0}^x g(t)\text{d}t & \\[8pt] &= 5\displaystyle\int_{0}^x \text{e}^{-t} \text{d}t - 3\displaystyle\int_{0}^x \text{e}^{-2t} \text{d}t & \text{ par linéarité de l'intégrale} \\[8pt] & = 5\displaystyle \left[-\text{e}^{-t} \right]_0^x -3\displaystyle \left[-\dfrac{1}{2}\text{e}^{-2t} \right]_0^x \\[8pt] &= 5\left( -\text{e}^{-x} +1 \right) - 3 \left( -\dfrac{1}{2}\text{e}^{-2x} + \dfrac{1}{2} \right) & \\[8pt] & = 5 - 5 \text{e}^{-x}+ \dfrac{3}{2}\text{e}^{-2x} -\dfrac{3}{2} \\[8pt] \mathcal{A}(x)& = \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{7}{2} \end{array} $$
$\mathcal{A}(x) = 2 \Leftrightarrow \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{7}{2} = 2 \Leftrightarrow \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{3}{2} = 0$ On pose $ X = \text{e}^{-x} $
Finalement, $\mathcal{A}(x) = 2 \Leftrightarrow x = \ln 3$.
- Vues: 45009
