Baccalauréat S Antilles-Guyane 19 juin 2014
Exercice 1 5 points
Les parties A et B sont indépendantes Les résultats seront arrondis à $10^{-4}$ près
Partie A
Un ostréiculteur élève deux espèces d'huîtres : « la plate » et « la japonaise » .
Chaque année, les huîtres plates représentent 15 %de sa production.
Les huîtres sont dites de calibre n° 3 lorsque leur masse est comprise entre 66g et 85g.
Seulement 10 %des huîtres plates sont de calibre n° 3, alors que 80 %des huîtres japonaises le sont.
- Le service sanitaire prélève une huître au hasard dans la production de l'ostréiculteur. On suppose que toutes les huitres ont la même chance d'être choisies. On considère les évènements suivants :
- $J$ : « l'huître prélevée est une huître japonaise » ,
- $C$ : « l'huître prélevée est de calibre n° 3 » .
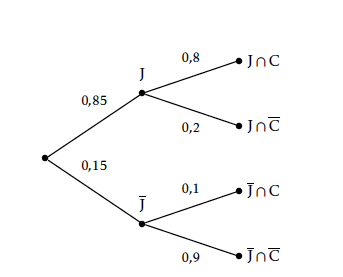
- Construire un arbre pondéré complet traduisant la situation.
- Calculer la probabilité que l'huître prélevée soit une huître plate de calibre n° 3.
- Justifier que la probabilité d'obtenir une huître de calibre n° 3 est $0,695$.
- Le service sanitaire a prélevé une huître de calibre n° 3. Quelle est la probabilité que ce soit une huître plate ?
- La masse d'une huître peut être modélisée par une variable aléatoire $X$ suivant la loi normale de moyenne $\mu = 90$ et d'écart-type $\sigma = 2$.
- Donner la probabilité que l'huître prélevée dans la production de l'ostréiculteur ait une masse comprise entre 87g et 89g.
- Donner $P(X \geqslant 91)$.
Partie B
Cet ostréiculteur affirme que 60 %de ses huîtres ont une masse supérieure à 91 g. Un restaurateur souhaiterait lui acheter une grande quantité d'huîtres mais il voudrait, auparavant, vérifier l'affirmation de l'ostréiculteur. Le restaurateur achète auprès de cet ostréiculteur 10 douzaines d'huîtres qu'on considèrera comme un échantillon de $120$ huîtres tirées au hasard. Sa production est suffisamment importante pour qu'on l'assimile à un tirage avec remise. Il constate que $65$ de ces huîtres ont une masse supérieure à 91 g.
- Soit $F$ la variable aléatoire qui à tout échantillon de $120$huîtres associe la fréquence de celles qui ont une masse supérieure à 91g. Après en avoir vérifié les conditions d'application, donner un intervalle de fluctuation asymptotique au seuil de 95 % de la variable aléatoire $F$.
- Que peut penser le restaurateur de l'affirmation de l'ostréiculteur ?
Correction de l'exercice 1 (5 points)
Partie A
Un ostréiculteur élève deux espèces d'huîtres : « la plate » et « la japonaise » .
Chaque année, les huîtres plates représentent 15 %de sa production.
Les huîtres sont dites de calibre n° 3 lorsque leur masse est comprise entre 66g et 85g.
Seulement 10 %des huîtres plates sont de calibre n° 3, alors que 80 %des huîtres japonaises le sont.
- Le service sanitaire prélève une huître au hasard dans la production de l'ostréiculteur. On suppose que toutes les huitres ont la même chance d'être choisies. On considère les évènements suivants :
- $J$ : « l'huître prélevée est une huître japonaise » ,
- $C$ : « l'huître prélevée est de calibre n° 3 » .
- Construire un arbre pondéré complet traduisant la situation.
- Calculer la probabilité que l'huître prélevée soit une huître plate de calibre n° 3. On cherche donc $P\left( \bar{J} \cap C \right) = 0,15 \times 0,1 = 0,015$
- Justifier que la probabilité d'obtenir une huître de calibre n° 3 est $0,695$. D’après la propriété des probabilités totales :
- Le service sanitaire a prélevé une huître de calibre n° 3. Quelle est la probabilité que ce soit une huître plate ? On cherche à calculer :
- La masse d'une huître peut être modélisée par une variable aléatoire $X$ suivant la loi normale de moyenne $\mu = 90$ et d'écart-type $\sigma = 2$.
- Donner la probabilité que l'huître prélevée dans la production de l'ostréiculteur ait une masse comprise entre 87g et 89g. D’après la calculatrice $P(87 \le X \le 89) \approx 0,2417$
- Donner $P(X \geqslant 91)$. $P(X \ge 91) = 0,5 – P(90 \le X \le 91) \approx 0,3085$
$$\begin{array} \\P(C) &= P(J \cap C) + P\left( \bar{J} \cap C \right) \\
&=0,85 \times 0,8 + 0,015 \\
&= 0,695
\end{array}$$
$$\begin{array}\\ P_C\left( \bar{J} \right) & = \dfrac{P\left( C \cap \bar{J} \right)}{P(C)} \\ &= \dfrac{0,015}{0,695} \\ &=\dfrac{3}{139} \\ & \approx 0,0216 \end{array}$$
Partie B
Cet ostréiculteur affirme que 60 %de ses huîtres ont une masse supérieure à 91 g. Un restaurateur souhaiterait lui acheter une grande quantité d'huîtres mais il voudrait, auparavant, vérifier l'affirmation de l'ostréiculteur. Le restaurateur achète auprès de cet ostréiculteur 10 douzaines d'huîtres qu'on considèrera comme un échantillon de $120$ huîtres tirées au hasard. Sa production est suffisamment importante pour qu'on l'assimile à un tirage avec remise. Il constate que $65$ de ces huîtres ont une masse supérieure à 91 g.
- Soit $F$ la variable aléatoire qui à tout échantillon de $120$ huîtres associe la fréquence de celles qui ont une masse supérieure à 91g. Après en avoir vérifié les conditions d'application, donner un intervalle de fluctuation asymptotique au seuil de 95 % de la variable aléatoire $F$. $n = 120 \ge 30$, $np = 120 \times 0,6 = 72 \ge 5$ et $n(1-p) = 48 \ge 5$
- Que peut penser le restaurateur de l'affirmation de l'ostréiculteur ? La fréquence observée est $f = \dfrac{65}{120} \approx 0,5417 \in I_{120}$.
Par conséquent un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$$\begin{array}\\ I_{120} &= \left[0,6 - 1,96 \times \dfrac{\sqrt{0,6 \times 0,4}}{\sqrt{120}};0,6 + 1,96 \times \dfrac{\sqrt{0,6 \times 0,4}}{\sqrt{120}} \right] \\ & \approx 0,5123;0,6877] \end{array}$$
L’ostréiculteur a donc raison d’affirmer que $60\%$ de ses huitres ont une masse supérieure à $91$g avec une marge d’erreur de $5\%$.
Exercice 2 6 points
On considère la fonction $f$ définie et dérivable sur l'ensemble $\mathbb{R}$ des nombres réels par \[f(x) = x + 1 + \dfrac{x}{\text{e}^x}.\]
On note $\mathcal{C}$ sa courbe représentative dans un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$.
Partie A
- Soit $g$ la fonction définie et dérivable sur l'ensemble $\mathbb{R}$ par \[g(x) = 1 - x + \text{e}^x.\] Dresser, en le justifiant, le tableau donnant les variations de la fonction $g$ sur $\mathbb{R}$ (les limites de $g$ aux bornes de son ensemble de définition ne sont pas attendues). En déduire le signe de $g(x)$.
- Déterminer la limite de $f$ en $- \infty$ puis la limite de $f$ en $+ \infty$.
- On appelle $f'$ la dérivée de la fonction $f$ sur $\mathbb{R}$. Démontrer que, pour tout réel $x$, \[f'(x) = \text{e}^{- x}g(x).\]
- En déduire le tableau de variation de la fonction $f$ sur $\mathbb{R}$.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution réelle $\alpha$ sur $\mathbb{R}$. Démontrer que $-1 < \alpha < 0$.
-
- Démontrer que la droite $T$ d'équation $y = 2x + 1$ est tangente à la courbe $\mathcal{C}$ au point d'abscisse $0$.
- Étudier la position relative de la courbe $\mathcal{C}$ et de la droite $T$.
Partie B
- Soit $H$ la fonction définie et dérivable sur $\mathbb{R}$ par \[H(x) = (- x - 1)\text{e}^{- x}.\] Démontrer que $H$ est une primitive sur $\mathbb{R}$ de la fonction $h$ définie par $h(x) = x\text{e}^{- x}$.
- On note $\mathcal{D}$ le domaine délimité par la courbe $\mathcal{C}$, la droite $T$ et les droites d'équation $x = 1$ et $x = 3$. Calculer, en unité d'aire, l'aire du domaine $\mathcal{D}$.
Correction de l'exercice 2 (6 points)
On note $\mathcal{C}$ sa courbe représentative dans un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$.
Partie A
- Soit $g$ la fonction définie et dérivable sur l'ensemble $\mathbb{R}$ par \[g(x) = 1 - x + \text{e}^x.\] Dresser, en le justifiant, le tableau donnant les variations de la fonction $g$ sur $\mathbb{R}$ (les limites de $g$ aux bornes de son ensemble de définition ne sont pas attendues). En déduire le signe de $g(x)$. $g’(x) = -1 + \text{e}^x$
- Déterminer la limite de $f$ en $- \infty$ puis la limite de $f$ en $+ \infty$. $\lim\limits_{n \rightarrow -\infty} x+1 = -\infty$ $\quad$ $\lim\limits_{n \rightarrow -\infty} \dfrac{1}{\text{e}^x} = +\infty$ donc $\lim\limits_{n \rightarrow -\infty} \dfrac{x}{\text{e}^x}=-\infty$
- On appelle $f'$ la dérivée de la fonction $f$ sur $\mathbb{R}$. Démontrer que, pour tout réel $x$, \[f'(x) = \text{e}^{- x}g(x).\] $$\begin{array}\\ f’(x) &= 1 + \dfrac{\text{e}^x – x\text{e}^x}{\text{e}^2x} \\ &= 1 + \dfrac{1 -x}{\text{e}^x} \\ &=\dfrac{\text{e}^x + 1 – x}{\text{e}^x} \\ &=\text{e}^{-x}g(x) \end{array}$$
- En déduire le tableau de variation de la fonction $f$ sur $\mathbb{R}$. D’après le tableau de variations de la fonction $g$ on constate que $g(x) > 0$ pour tout $x$. On sait de plus que la fonction exponentielle est strictement positive.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution réelle $\alpha$ sur $\mathbb{R}$. Démontrer que $-1 < \alpha < 0$. La fonction $f$ est continue (car dérivable) et strictement croissante sur $\mathbb{R}$.
-
- Démontrer que la droite $T$ d'équation $y = 2x + 1$ est tangente à la courbe $\mathcal{C}$ au point d'abscisse $0$. Une équation de la tangente est de la forme $y=f'(a)(x-a)+f(a)$.
- Étudier la position relative de la courbe $\mathcal{C}$ et de la droite $T$. Pour étudier la position relative de la courbe $\mathscr{C}$ et de $T$ on étudie le signe de :
$f'(0) = 2$ et $f(0) = 1$. Donc la tangente en $0$ à $\mathscr{C}$ a pour équation $y =2x+1$
$$\begin{array}\\ f(x) - (2x+1) &= x+1 + \dfrac{x}{\text{e}^x} -2x - 1 \\ &= -x + \dfrac{x}{\text{e}^x} \\ &= x\dfrac{ -\text{e}^x + 1}{\text{e}^x} \\ &=\dfrac{-xg'(x)}{\text{e}^x} \le 0 \end{array}$$
La droite $T$ est donc toujours au-dessus de la courbe $\mathscr{C}$.
Etudions le signe de $g’(x)$
$$\begin{array}\\ g’(x) > 0 & \Leftrightarrow -1 + \text{e}^x > 0 \\ & \Leftrightarrow \text{e}^x > 1 \\ & \Leftrightarrow x > 0\\ \end{array}$$
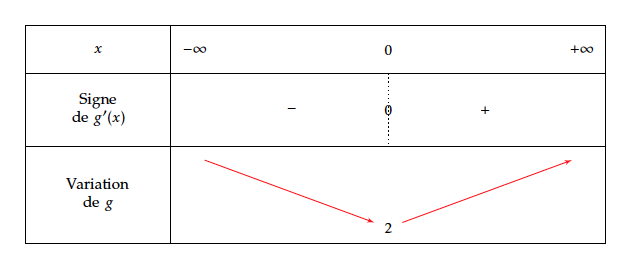
Par conséquent :
$$\lim\limits_{n \rightarrow -\infty} f(x) = -\infty$$
$\lim\limits_{n \rightarrow +\infty} x + 1 = +\infty$ $\quad$ $\lim\limits_{n \rightarrow +\infty} \dfrac{\text{e}^x}{x} = +\infty$ donc $\lim\limits_{n \rightarrow +\infty} \dfrac{x}{\text{e}^x} = 0$
Par conséquent :
$$\lim\limits_{n \rightarrow +\infty} f(x) = +\infty$$
Par conséquent :
$$\forall x\in \mathbb{R}, f’(x) > 0$$
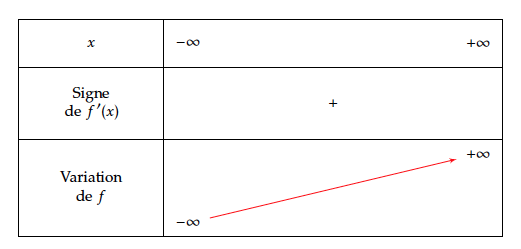
De plus $\lim\limits_{n \rightarrow -\infty} f(x) = -\infty$ et $\lim\limits_{n \rightarrow +\infty} f(x) = +\infty$
$0 \in ]-\infty;+\infty[$.
D'après le théorème de la bijection (ou théorème des valeurs intermédiaires), l'équation $f(x)=0$ possède donc une unique solution sur $\mathbb{R}$.
$~$
$f(-1) = -\text{e}^{-1} < 0$ et $f(0) = 1 > 0$ donc $-1 \alpha < 0$.
Partie B
- Soit $H$ la fonction définie et dérivable sur $\mathbb{R}$ par \[H(x) = (- x - 1)\text{e}^{- x}.\] Démontrer que $H$ est une primitive sur $\mathbb{R}$ de la fonction $h$ définie par $h(x) = x\text{e}^{- x}$. $H'(x) = -\text{e}^{-x} - (-x-1)\text{e}^{-x} $ $= x\text{e}^{-x} = h(x)$
- On note $\mathcal{D}$ le domaine délimité par la courbe $\mathcal{C}$, la droite $T$ et les droites d'équation $x = 1$ et $x = 3$. Calculer, en unité d'aire, l'aire du domaine $\mathcal{D}$. L'aire cherchée est :
Donc $H$ est une primitive de $h$ sur $\mathbb{R}$.
$$\begin{array}\\ \mathscr{A} &=\int_1^3(f(x) - (2x+1))\text{d}x \\ &=\int_1^3 (-x+h(x)) \text{d}x \\ &=\left[\dfrac{-x^2}{2} + H(x) \right]_1^3 \\ &= \dfrac{9}{2} – 4\text{e}^{-3} – \dfrac{1}{2} – (-2)\text{e}^{-1} \\ &= 4 - 4\text{e}^{-3} +2\text{e}^{-1} \text{ u.a} \end{array}$$
Exercice 3 4 points
Pour chacune des quatre propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
L'espace est muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j},\vec{k}\right)$ .
On considère les points A(1;2;5), B$(-1;6;4)$, C$(7;- 10;8)$ et D$(-1;3;4)$.
- Proposition 1 : Les points A, B et C définissent un plan.
- On admet que les points A, B et D définissent un plan.
Proposition 2 : Une équation cartésienne du plan (ABD) est $x - 2z + 9 = 0$. - Proposition 3 : Une représentation paramétrique de la droite (AC) est \[\left\{\begin{array}{l c l} x &=& \dfrac{3}{2}t - 5\\ y &=& - 3t + 14\\ z &=&- \dfrac{3}{2}t + 2 \end{array}\right. \quad t \in\mathbb{R}\]
- Soit $\mathcal{P}$ le plan d'équation cartésienne $2x - y + 5z + 7 = 0$ et $\mathcal{P}'$ le plan d'équation cartésienne $- 3x - y + z + 5 = 0$.
Proposition 4 : Les plans $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles.
Exercice 3 4 points
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte.
Une absence de réponse n'est pas pénalisée.
L'espace est muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j},\vec{k}\right)$ .
On considère les points A(1;2;5), B$(-1;6;4)$, C$(7;- 10;8)$ et D$(-1;3;4)$.
- Proposition 1 : Les points A, B et C définissent un plan.
- On admet que les points A, B et D définissent un plan.
Proposition 2 : Une équation cartésienne du plan (ABD) est $x - 2z + 9 = 0$. - Proposition 3 : Une représentation paramétrique de la droite (AC) est \[\left\{\begin{array}{l c l} x &=& \dfrac{3}{2}t - 5\\ y &=& - 3t + 14\\ z &=&- \dfrac{3}{2}t + 2 \end{array}\right. \quad t \in\mathbb{R}\]
- Soit $\mathcal{P}$ le plan d'équation cartésienne $2x - y + 5z + 7 = 0$ et $\mathcal{P}'$ le plan d'équation cartésienne $- 3x - y + z + 5 = 0$.
Proposition 4 : Les plans $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles.
Proposition 1 : FAUX
$\vec{AB}(-2;4;-1)$ et $\vec{AC}(6;-12;3) = -3\vec{AB}$
Les $2$ vecteurs sont colinéaires, ils ne définissent donc pas de plan.
Proposition 2 : VRAI
Regardons si les coordonnées de chacun des points vérifient l’équation donnée :
Pour $A$ : $ 1 – 10 + 9 = 0$ $\surd$
Pour $B$ : $-1 -8 + 9 = 0$ $\surd$
Pour $D$ : $-1 – 8 + 9 = 0$ $\surd$
L’équation donnée est donc bien une équation de $(ABD)$.
Proposition 3 : FAUX
Si $t=4$ alors $x=1$, $y=2$ et $z=-4$. Par conséquent le point $A$ n’appartient pas à la droite dont la représentation paramétrique est fournie.
Proposition 4 : FAUX
Un vecteur normal à $\mathscr{P}$ est $\vec{n}(2;-1;5)$.
Un vecteur normal à $\mathscr{P}’$ est $\vec{n}(-3;-1;1)$.
C’est $2$ vecteurs ne sont clairement pas colinéaires (en revanche ils sont orthogonaux!)
Exercice 4 5 points
Soit la suite numérique $\left(u_{n}\right)$ définie sur l'ensemble des entiers naturels $\mathbb{N}$ par \[\left\{\begin{array}{r c l} u_{0}& =& 2\\ \text{et pour tout entier naturel }\:n,\: u_{n+1} &=& \dfrac{1}{5} u_{n} + 3 \times 0,5^n. \end{array}\right.\]
-
- Recopier et, à l'aide de la calculatrice, compléter le tableau des valeurs de la suite $\left(u_{n}\right)$ approchées à $10^{-2}$ près: $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline n& 0&1&2&3&4&5&6&7&8\\ \hline u_{n}&2&&&&&&&&\\ \hline \end{array}$$
- D'après ce tableau, énoncer une conjecture sur le sens de variation de la suite $\left(u_{n}\right)$.
-
- Démontrer, par récurrence, que pour tout entier naturel $n$ non nul on a \[u_{n} \geqslant \dfrac{15}{4} \times 0,5^n.\]
- En déduire que, pour tout entier naturel $n$ non nul, $u_{n+1} - u_{n} \leqslant 0$.
- Démontrer que la suite $\left(u_{n}\right)$ est convergente.
- On se propose, dans cette question de déterminer la limite de la suite $\left(u_{n}\right)$. Soit $\left(v_{n}\right)$ la suite définie sur $\mathbb{N}$ par $v_{n} = u_{n} - 10 \times 0,5^n$.
- Démontrer que la suite $\left(v_{n}\right)$ est une suite géométrique de raison $\dfrac{1}{5}$. On précisera le premier terme de la suite $\left(v_{n}\right)$.
- En déduire, que pour tout entier naturel $n$, \[u_{n} = - 8 \times \left(\dfrac{1}{5}\right)^n + 10 \times 0,5^n.\]
- Déterminer la limite de la suite $\left(u_{n}\right)$
- Recopier et compléter les lignes (1), (2) et (3) de l'algorithme suivant, afin qu'il affiche la plus petite valeur de $n$ telle que $u_{n} \leqslant 0,01$. $$\begin{array} {|l| l|} \hline \text{Entrée :}& n \text{ et } u \text{ sont des nombres}\\ \text{Initialisation :}& n \text{ prend la valeur 0}\\ & u \text{ prend la valeur 2}\\ \text{Traitement :}&\text{ Tant que ... (1)}\\ &\ n \text{ prend la valeur ... (2)}\\ & u \text{ prend la valeur ... (3)}\\ &\text{ Fin Tant que}\\ \text{Sortie :}&\text{Afficher } n\\ \hline \end{array}$$
Correction de l'exercice 4 5 points
-
- Recopier et, à l'aide de la calculatrice, compléter le tableau des valeurs de la suite $\left(u_{n}\right)$ approchées à $10^{-2}$ près: $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline n& 0&1&2&3&4&5&6&7&8\\ \hline u_{n}&2& 3,4& 2,18& 1,19 & 0,61 & 0,31 & 0,16 & 0,08& 0,04\\ \hline \end{array}$$
- D'après ce tableau, énoncer une conjecture sur le sens de variation de la suite $\left(u_{n}\right)$. Il semblerait que la suite $(u_n)$ soit décroissante.
-
- Démontrer, par récurrence, que pour tout entier naturel $n$ non nul on a \[u_{n} \geqslant \dfrac{15}{4} \times 0,5^n.\] Initialisation : si $n=1$ alors $u_1 = 3,4$ et $\dfrac{15}{4} \times 0,5 = 1,875$. Par conséquent $u_1 \ge \dfrac{15}{4} \times 0,5$
- En déduire que, pour tout entier naturel $n$ non nul, $u_{n+1} - u_{n} \leqslant 0$. $$\begin{array} \\u_{n+1} – u_n &= \dfrac{1}{5}u_n + 3\times 0,5^n – u_n \\ &= -\dfrac{4}{5} u_n + 3 \times 0,5^n \\ & \le -\dfrac{4}{5} \times \dfrac{15}{4} \times 0,5^n + 3 \times 0,5^n \\ & \le -3 \times 0,5^n + 3 \times 0,5^n \end{array}$$
- Démontrer que la suite $\left(u_{n}\right)$ est convergente. La suite $(u_n)$ est donc décroissante et minorée par $0$. Par conséquent, elle converge.
La propriété est vraie au rang $1$
$~$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n \ge \dfrac{15}{4} \times 0,5^n$
Alors :
$$\begin{array}\\ u_{n+1} &= \dfrac{1}{5}u_n + 3 \times 0,5^n \\ & \ge \dfrac{1}{5} \times \dfrac{15}{4} \times 0,5^n + 3 \times 0,5^n \\ & \ge \dfrac{3}{4} \times 0,5^n + 3 \times 0,5^n \\ & \ge \dfrac{15}{4} \times 0,5^n \\ & \ge \dfrac{15}{4} \times 0,5 \times 0,5^n \\ & \ge \dfrac{15}{4} \times 0,5^{n+1} \end{array} $$
La propriété est donc vraie au rang $n+1$.
$~$
Conclusion : La propriété est vraie au rang $1$. Si on la suppose vraie au rang $n$ elle est encore vraie au rang suivant.
Par conséquent, pour tout entier naturel non nul $n$ on a:
$$u_n \ge \dfrac{15}{4} \times 0,5^n$$
- On se propose, dans cette question de déterminer la limite de la suite $\left(u_{n}\right)$. Soit $\left(v_{n}\right)$ la suite définie sur $\mathbb{N}$ par $v_{n} = u_{n} - 10 \times 0,5^n$.
- Démontrer que la suite $\left(v_{n}\right)$ est une suite géométrique de raison $\dfrac{1}{5}$. On précisera le premier terme de la suite $\left(v_{n}\right)$. $$\begin{array}\\ v_{n+1}& = u_{n+1} – 10 \times 0,5^{n+1} \\ &= \dfrac{1}{5}u_n+3\times 0,5^n – 10 \times 0,5 \times 0,5^n \\ &= \dfrac{1}{5}u_n-2\times 0,5^n \\ &= \dfrac{1}{5} (u_n – 10 \times 0,5^n) \\ &=\dfrac{1}{5} v_n \end{array}$$
- En déduire, que pour tout entier naturel $n$, \[u_{n} = - 8 \times \left(\dfrac{1}{5}\right)^n + 10 \times 0,5^n.\] La suite $(v_n)$ est donc géométrique de raison $\dfrac{1}{5}$ et de premier terme $v_0 = 2 -10 = -8$
- Déterminer la limite de la suite $\left(u_{n}\right)$ Par conséquent $v_n = -8\times \left(\dfrac{1}{5} \right)^n$.
On en déduit donc que :
$$ \begin {array} \\u_n &= v_n + 10\times 0,5 ^n \\ &= -8\times \left(\dfrac{1}{5} \right)^n+ 10\times 0,5 ^n \end{array}$$ $\lim\limits_{n \rightarrow +\infty} \left(\dfrac{1}{5} \right)^n = 0$ car $-1 < \dfrac{1}{5} < 1$.
Pour la même raison on a : $\lim\limits_{n \rightarrow +\infty} 0,5^n = 0$
Par conséquent : $$\lim\limits_{n \rightarrow +\infty} u_n = 0$$ - Recopier et compléter les lignes (1), (2) et (3) de l'algorithme suivant, afin qu'il affiche la plus petite valeur de $n$ telle que $u_{n} \leqslant 0,01$. $$\begin{array} {|l| l|} \hline \text{Entrée :}& n \text{ et } u \text{ sont des nombres}\\ \text{Initialisation :}& n \text{ prend la valeur 0}\\ & u \text{ prend la valeur 2}\\ \text{Traitement :}&\text{ Tant que ... (1)}\\ &\ n \text{ prend la valeur ... (2)}\\ & u \text{ prend la valeur ... (3)}\\ &\text{ Fin Tant que}\\ \text{Sortie :}&\text{Afficher } n\\ \hline \end{array}$$ Entrée :
$\quad$ $n$ et $u$ sont des nombres
Initialisation :
$\quad$ $n$ prend la valeur $0$
$\quad$ $u$ prend la valeur $2$
Traitement :
$\quad$ Tant que $u > 0,01$
$\qquad$ $n$ prend la valeur $n+1$
$\qquad$ $u$ prend la valeur $ -8\times \left(\dfrac{1}{5} \right)^n+ 10\times 0,5 ^n$ $\quad$
Spécialité 5 points
En montagne, un randonneur a effectué des réservations dans deux types d'hébergements:
L'hébergement A et l'hébergement B.
Une nuit en hébergement A coûte 24 € et une nuit en hébergement B coûte 45 €.
Il se rappelle que le coût total de sa réservation est de 438 €.
On souhaite retrouver les nombres $x$ et $y$ de nuitées passées respectivement en hébergement A et en hébergement B
-
- Montrer que les nombres $x$ et $y$ sont respectivement inférieurs ou égaux à 18 et 9.
- Recopier et complèter les lignes (1), (2) et (3) de l'algorithme suivant afin qu'il affiche les couples ($x$ ; $y$) possibles. $$\begin{array}{|l|l|}\hline \text{Entrée :} & x \text{ et } y \text{ sont des nombres}\\ \text{Traitement :} & \text{ Pour } x \text{ variant de } 0 \ldots\ (1)\\& \text{ Pour } y \text{ variant de } 0 \ldots\ (2)\\ & \text{ Si } \ldots (3)\\ & \text{Afficher } x \text{ et } y\\ & \text{Fin Si }\\ & \text{ Fin Pour}\\ &\text{ Fin Pour}\\ \text{Fin traitement}&\\\hline \end{array}$$
- Justifier que le coût total de la réservation est un multiple de 3.
-
- Justifier que l'équation $8x + 15y = 1$ admet pour solution au moins un couple d'entiers relatifs.
- Déterminer une telle solution.
- Résoudre l'équation (E) : $8x + 15y = 146$ où $x$ et $y$ sont des nombres entiers relatifs.
- Le randonneur se souvient avoir passé au maximum 13 nuits en hébergement A.
Montrer alors qu'il peut retrouver le nombre exact de nuits passées en hébergement A et celui des nuits passées en hébergement B.
Calculer ces nombres.
Correction de l'exercice de Spécialité 5 points
L'hébergement A et l'hébergement B.
Une nuit en hébergement A coûte 24 € et une nuit en hébergement B coûte 45 €.
Il se rappelle que le coût total de sa réservation est de 438 €.
On souhaite retrouver les nombres $x$ et $y$ de nuitées passées respectivement en hébergement A et en hébergement B
-
- Montrer que les nombres $x$ et $y$ sont respectivement inférieurs ou égaux à 18 et 9. $\dfrac{438}{24} = 18,25$ et $\dfrac{438}{45} \approx 9,7$.
- Recopier et complèter les lignes (1), (2) et (3) de l'algorithme suivant afin qu'il affiche les couples ($x$ ; $y$) possibles. $$\begin{array}{|l|l|}\hline \text{Entrée :} & x \text{ et } y \text{ sont des nombres}\\ \text{Traitement :} & \text{ Pour } x \text{ variant de } 0 \ldots\ (1)\\& \text{ Pour } y \text{ variant de } 0 \ldots\ (2)\\ & \text{ Si } \ldots (3)\\ & \text{Afficher } x \text{ et } y\\ & \text{Fin Si }\\ & \text{ Fin Pour}\\ &\text{ Fin Pour}\\ \text{Fin traitement}&\\\hline \end{array}$$ Entrée :
Il ne peut donc pas avoir passé plus de $18$ nuits dans l’hébergement A et plus de $9$ nuits dans l’hébergement B.
$~$
Par conséquent $x \le 18$ et $y \le 9$.
$\quad$ $x$ et $y$ sont deux nombres
Traitement :
$\quad$ Pour $x$ variant de $0$ à $18$
$\qquad$ Pour $y$ variant de $0$ à $9$
$\qquad \quad$ Si $24x+45y=438$
$\qquad \qquad$ Afficher $x$ et $y$
$\qquad \quad$ Fin Si
$\qquad $ Fin Pour
$\quad$ Fin Pour
Fin traitement
- Justifier que le coût total de la réservation est un multiple de 3. Le coût total de la réservation est:
-
- Justifier que l'équation $8x + 15y = 1$ admet pour solution au moins un couple d'entiers relatifs. $8$ et $15$ sont premiers entre eux. D’après le théorème de Bezout, l’équation $8x+15y=1$ admet donc au moins un couple d’entiers relatifs solution.
- Déterminer une telle solution. $8\times 2 + 15 \times (-1) = 16 -15 = 1$
- Résoudre l'équation (E) : $8x + 15y = 146$ où $x$ et $y$ sont des nombres entiers relatifs. Le couple $(292;-146)$ est donc solution de l’équation $8x+15y=146$.
Le couple $(2;-1)$ est donc solution de l’équation $8x+15y=146$.
Soit $(x;y)$ un autre couple solution.
Par différence on obtient :
$$8(x-292)+15(y+146) = 0 \Leftrightarrow 8(x-292)=15(-y-146)$$
$8$ et $15$ sont premiers entre eux. D’après le théorème de Gauss, il existe alors un entier relatif $k$ tel que :
$ x-292 = 15k $ et $-y-146 = 8k$
Soit$ x = 292+15k$ et $y=-146 – 8k$
$~$
Réciproquement : soient $k \in \mathbb{Z}$ et $x=292+15k$ et $y=-146-8k$
Alors :
$$ \begin{array}\\ 8x+15y &=8(292+15k)+15(-146-8k) \\ &=2336 + 120k – 2190 – 120k \\ &=146 \end{array}$$
Les solutions de cette équation sont donc les couples $(292+15k;-146-8k)$ pour tout $k\in\mathbb{Z}$. - Le randonneur se souvient avoir passé au maximum 13 nuits en hébergement A.
Montrer alors qu'il peut retrouver le nombre exact de nuits passées en hébergement A et celui des nuits passées en hébergement B.
Calculer ces nombres. $438 = 3 \times 146$.
$$24x+45y = 3\times 8x+3\times 15y = 3(8x+15y)$$
C’est donc un multiple de $3$.
Notre problème de départ revient à trouver les couples $(x;y)$ tels que $8x+15y=146$.
On sait que $x \le 13$ par conséquent :
$$\begin{array}\\ 0 \le 292 + 15k \le 13 & \Leftrightarrow -292 \le 15k \le -279 \\ & \Leftrightarrow \dfrac{-292}{15} \le k \le \dfrac{-279}{15} \\ & \Leftrightarrow k = -19\\ \end{array}$$ Cela signifie donc que $x= 7$ et donc $y = \dfrac{146-8\times 7}{15} = 6$
$~$
Le randonneur a donc passé $7$ nuits dans l’hébergement A et $6$ dans l’hébergement B.
- Vues: 43108
