Baccalauréat S Asie 19 juin 2014 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
Soit $n$ un entier naturel supérieur ou égal à 1. On note $f_{n}$ la fonction définie pour tout réel $x$ de l'intervalle [0 ; 1] par \[f_{n}(x) = \dfrac{1}{1 + x^n}.\] Pour tout entier $n \geqslant 1$, on définit le nombre $I_{n}$ par \[I_{n} = \int_{0}^1 f_{n}(x)\:\text{d}x = \int_{0}^1 \dfrac{1}{1 + x^n}\:\text{d}x.\]
- Les représentations graphiques de certaines fonctions $f_{n}$ obtenues à l'aide d'un logiciel sont tracées ci-après.
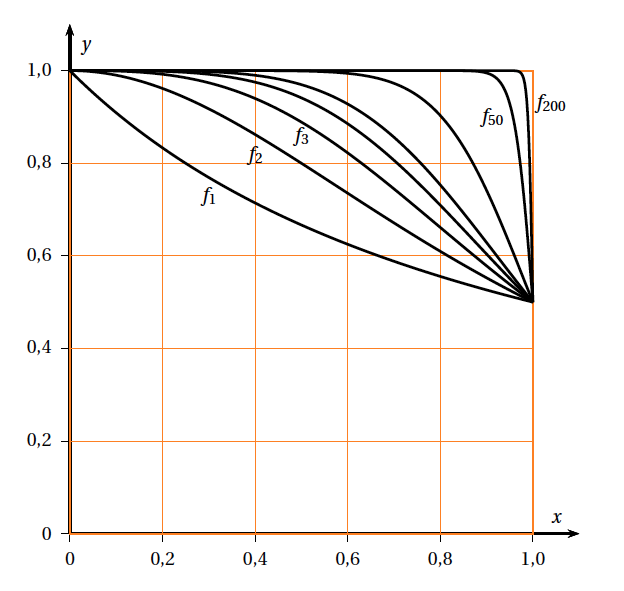
En expliquant soigneusement votre démarche, conjecturer, pour la suite $\left(I_{n}\right)$ l'existence et la valeur éventuelle de la limite, lorsque $n$ tend vers $+ \infty$. Les fonctions $f_n$ sont continues et positives sur [0; 1], donc $I_n$ est l'aire du domaine limité par $\mathcal{C}_{n}$ la courbe représentative de $f_{n}$, l'axe des abscisses et les droites d'équation $x=0$ et $x=1$. - Calculer la valeur exacte de $I_{1}$. $$\begin{array}\\ I_1 &= \int_0^1 \left(\dfrac{1}{1 + x^n}\right) \text{d}x \\ &= \left[ \ln \left|1+x \right |\right]_0^1 \\ &= \ln 2 -\ln 1 \\ &=\ln 2\\ \end{array}$$
-
- Démontrer que, pour tout réel $x$ de l'intervalle [0 ; 1] et pour tout entier naturel $n \geqslant 1$, on a : \[\dfrac{1}{1 + x^n} \leqslant 1.\] On a pour tout réel $x$ de de l'intervalle [0 ; 1] : $$\begin{array}\\ 0 \leq x \leq 1 & \\ 0 \leq x^n \leq 1 & \text{ car } x\mapsto x^n \text{ est strictement croissante sur [0 ; 1] } \\ 1 \leq 1+x ^n \leq 2 & \text{ en ajoutant 1 ... } \\ 1 \geq \dfrac{1}{1+x^n} \geq \dfrac{1}{2} & \text{ car } x\mapsto \dfrac{1}{x} \text{ est strictement décroissante sur } ]0 ; +\infty[ \\ \end{array}$$ Ainsi pour tout réel $x$ de l'intervalle [0 ; 1] et pour tout entier naturel $n \geqslant 1$, on a :$\dfrac{1}{1 + x^n} \leqslant 1.$
- En déduire que, pour tout entier naturel $n \geqslant 1$, on a : $I_{n} \leqslant 1$.
On a pour tout réel $x$ de de l'intervalle [0 ; 1] : $$\begin{array}\\ \dfrac{1}{1 + x^n} \leqslant 1 & \\ \int_0^1 \left(\dfrac{1}{1 + x^n}\right) \text{d}x \leq \int_0^1 1 \text{d}x& \text{ car 0>1 } \text{ en intégrant l'inégalité précédente } \\ \int_0^1 \left(\dfrac{1}{1 + x^n}\right) \text{d}x \leq \left[ x\right]_0^1& \\ I_n \leq 1& \\ \end{array}$$
- Démontrer que, pour tout réel $x$ de l'intervalle [0 ; 1] et pour tout entier naturel $n \geqslant 1$, on a : \[1 - x^n \leqslant \dfrac{1}{1 + x^n}.\] On a pour tout réel $x$ de l'intervalle [0 ; 1] : $$\begin{array}\\ \dfrac{1}{1 + x^n} -\left(1-x ^n\right ) & =\dfrac{1}{1 + x^n} -\dfrac{\left(1-x ^n\right )\left(1+x ^n\right )}{1 + x^n} \\ & = \dfrac{1-\left(1-x ^{2n}\right ) }{1 + x^n}\\ & = \dfrac{ x ^{2n} }{1 + x^n}\\ \end{array}$$ Or ici $x \in [0 ; 1]$ d'où $\left.\begin{array}{l} x ^{2n}\geq 0\\ 1 + x^n>0 \end{array}\right\}$ par quotient on obtient: $\dfrac{ x ^{2n} }{1 + x^n}\geq 0$
- Calculer l'intégrale $\displaystyle\int_{0}^1 \left( 1 - x^n\right)\:\text{d}x$. $$\begin{array}\\ \displaystyle\int_{0}^1 \left( 1 - x^n\right)\:\text{d}x &= = \left[ x- \dfrac{x^{n+1}}{n+1}\right]_0^1 \\ &= 1- \dfrac{1^{n+1}}{n+1} -0\\ &=1- \dfrac{1}{n+1}\\ \end{array}$$
- À l'aide des questions précédentes, démontrer que la suite $\left(I_{n}\right)$ est convergente et déterminer sa limite. On a pour tout réel $x$ de de l'intervalle [0 ; 1] : $$\begin{array}\\ 1 - x^n & \leq \dfrac{1}{1 + x^n} & \leq 1& \\ \int_0^1 \left( 1 - x^n \right) \text{d}x &\leq \int_0^1 \left(\dfrac{1}{1 + x^n}\right) \text{d}x &\leq \int_0^1 1 \text{d}x& \text{ car 0>1 } \text{ en intégrant l'inégalité précédente } \\ 1- \dfrac{1}{n+1} &\leq I_n &\leq 1 &\text{ calculs précédents} \\ \end{array}$$ Or $\lim\limits_{n \to +\infty} 1- \dfrac{1}{n+1}= \lim\limits_{n \to +\infty}1=1$; d'après le théorème des gendarmes, on conclut : $\lim\limits_{n \to +\infty}I_n=1$
- On considère l'algorithme suivant : $$\begin{array}{|l| l|}\hline \text{Variables :}& n,\:p \text{ et } k \text{ sont des entiers naturels }\\ & x \text{ et } I \text{ sont des réels}\\ &\\ \text{Initialisation :}& I \text{ prend la valeur 0}\\ &\\ \text{Traitement :}& \text{Demander un entier } n \geqslant 1\\ & \text{ Demander un entier } p \geqslant 1\\ &\text{ Pour } k \text{ allant de } 0 \text{ à } p - 1 \text{ faire :}\\ & x \text{ prend la valeur } \dfrac{k}{p}\\ & I \text{ prend la valeur } I + \dfrac{1}{1 + x^n} \times \dfrac{1}{p}\\ &\text{Fin Pour} \\ &\text{ Afficher } I\\ \hline \end{array}$$
- Quelle valeur, arrondie au centième, renvoie cet algorithme si l'on entre les valeurs $n = 2$ et $p = 5$ ?
On justifiera la réponse en reproduisant et en complétant le tableau suivant avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme.
Les valeurs de $I$ seront arrondies au millième. $$\begin{array}{ |c|c|c|}\hline k& x&I\\ \hline 0&0&0,2\\ \hline 1 & 0,2&0,392\\ \hline2 &0,4& 0,565\\ \hline 3 & 0,6&0,712\\ \hline 4&0,8& 0,834\\ \hline \end{array}$$ - Expliquer pourquoi cet algorithme permet d'approcher l'intégrale $I_{n}$.
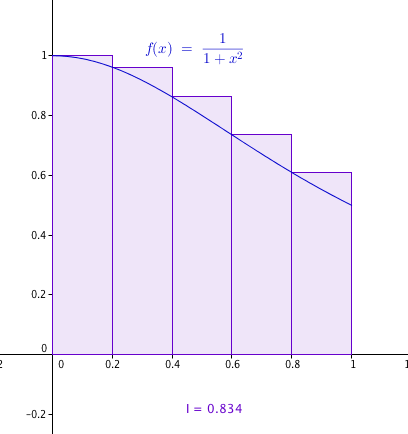
- Quelle valeur, arrondie au centième, renvoie cet algorithme si l'on entre les valeurs $n = 2$ et $p = 5$ ?
La suite $\left(I_{n}\right)$ semble, au vu du graphique, croissante majorée par 1, laire du carré de côté 1.
On conjecture donc $\lim\limits_{n \to +\infty}~I_n=1 $.
comme $ \dfrac{1}{1 + x^n} -\left(1-x ^n\right )\geq 0$, on déduit : $1 - x^n \leqslant \dfrac{1}{1 + x^n}$ sur l'intervalle [0 ; 1].
- Vues: 24061
