Baccalauréat S Liban 27 mai 2014

 

 

Exercice 1 5 points

Commun à tous les candidats

Les trois parties A, B et C peuvent être traitées de façon indépendante.
Les probabilités seront arrondies au dix millième.

Un élève doit se rendre à son lycée chaque matin pour 8 h 00. Pour cela, il utilise, selon les jours, deux moyens de transport : le vélo ou le bus.

Partie A :

L'élève part tous les jours à 7 h 40 de son domicile et doit arriver à 8 h 00 à son lycée.

Il prend le vélo 7 jours sur 10 et le bus le reste du temps.

Les jours où il prend le vélo, il arrive à l'heure dans $ 99,4 \%$ des cas et lorsqu'il prend le bus, il arrive en retard dans $5\,\%$ des cas.

On choisit une date au hasard en période scolaire et on note $V$ l'évènement « L'élève se rend au lycée à vélo »,

$B$ l'évènement « l'élève se rend au lycée en bus » et $R$ l'évènement « L'élève arrive en retard au lycée ».

1. Traduire la situation par un arbre de probabilités.
2. Déterminer la probabilité de l'évènement $V \cap R$.
3. Démontrer que la probabilité de l'évènement $R$ est $ 0,0192 $
4. Un jour donné, l'élève est arrivé en retard au lycée. Quelle est la probabilité qu'il s'y soit rendu en bus?

Partie B : le vélo

On suppose dans cette partie que l'élève utilise le vélo pour se rendre à son lycée. Lorsqu'il utilise le vélo, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par une variable aléatoire $T$ qui suit le loi normale d'espérance $\mu = 17$ et d'écart-type $\sigma = 1,2$.

1. Déterminer la probabilité que l'élève mette entre 15 et 20 minutes pour se rendre à son lycée.
2. Il part de son domicile à vélo à 7 h 40. Quelle est la probabilité qu'il soit en retard au lycée?
3. L'élève part à vélo. Avant quelle heure doit-il partir pour arriver à l'heure au lycée avec une probabilité de $ 0,9 $ ? Arrondir le résultat à la minute près.

Partie C : le bus

Lorsque l'élève utilise le bus, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par une variable aléatoire $T'$ qui suit la loi normale d'espérance $\mu' = 15$ et d'écart-type $\sigma'$.

On sait que la probabilité qu'il mette plus de 20 minutes pour se rendre à son lycée en bus est de $0,05$. On note $Z'$ la variable aléatoire égale à $\dfrac{T'-15}{\sigma'}$

1. Quelle loi la variable aléatoire $Z'$ suit-elle ?
2. Déterminer une valeur approchée à $0,01$ près de l'écart-type $\sigma'$ de la variable aléatoire $T'$.

 

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

Les trois parties A, B et C peuvent être traitées de façon indépendante.
Les probabilités seront arrondies au dix millième.

Un élève doit se rendre à son lycée chaque matin pour 8 h 00. Pour cela, il utilise, selon les jours, deux moyens de transport : le vélo ou le bus.

Partie A :

L'élève part tous les jours à 7 h 40 de son domicile et doit arriver à 8 h 00 à son lycée.

Il prend le vélo 7 jours sur 10 et le bus le reste du temps.

Les jours où il prend le vélo, il arrive à l'heure dans $ 99,4 \%$ des cas et lorsqu'il prend le bus, il arrive en retard dans $5\,\%$ des cas.

On choisit une date au hasard en période scolaire et on note $V$ l'évènement « L'élève se rend au lycée à vélo »,

$B$ l'évènement « l'élève se rend au lycée en bus » et $R$ l'évènement « L'élève arrive en retard au lycée ».

1. Traduire la situation par un arbre de probabilités.

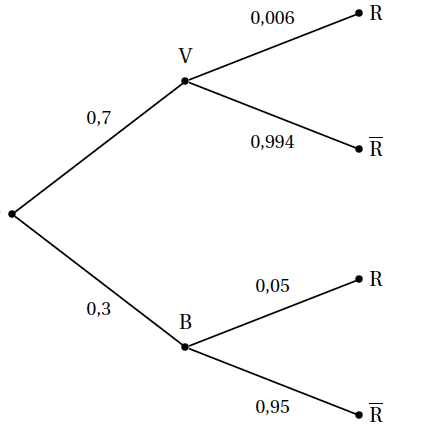
1. Déterminer la probabilité de l'évènement $V \cap R$.
D'après l'arbre ci-dessus $P\big(V \cap R\big)=0,7\times0,006=0,0042$.
2. Démontrer que la probabilité de l'évènement $R$ est $ 0,0192 $
D'après l'arbre ci-dessus, la probabilité de l'évènement R est \[P(R)=P\big(V \cap R\big)+P\big(B \cap R\big)= 0,0042 + 0,3 \times 0,05 = 0,0192 \]
3. Un jour donné, l'élève est arrivé en retard au lycée. Quelle est la probabilité qu'il s'y soit rendu en bus?
On cherche à déterminer $P_{R}\big(B\big)$: \[P_{R}\big(B\big)=\dfrac{P\big(B\cap R\big)}{P\big(R\big)}=\dfrac{ 0,3 \times 0,05 }{ 0,0192 } = 0,78125 \]

Partie B : le vélo

On suppose dans cette partie que l'élève utilise le vélo pour se rendre à son lycée. Lorsqu'il utilise le vélo, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par une variable aléatoire $T$ qui suit le loi normale d'espérance $\mu = 17$ et d'écart-type $\sigma = 1,2$.

1. Déterminer la probabilité que l'élève mette entre 15 et 20 minutes pour se rendre à son lycée.
Cela revient à calculer $P\big(15\leqslant T\leqslant 20\big)$. À la calculatrice, nous obtenons, $P\big(15\leqslant T\leqslant 20\big)= 0,946 $
2. Il part de son domicile à vélo à 7 h 40. Quelle est la probabilité qu'il soit en retard au lycée?
Il sera en retard au lycée si il met plus de 20 minutes pour effectuer le trajet. On cherche donc la probabilité de l'évènement « $T \geqslant 20$ » . À la calculatrice, nous obtenons \[P\big( T\geqslant 20\big)= 0,0062 \]
3. L'élève part à vélo. Avant quelle heure doit-il partir pour arriver à l'heure au lycée avec une probabilité de $ 0,9 $ ? Arrondir le résultat à la minute près.
4. On cherche la durée maximale de son temps de parcours $T_0$ (en minutes) tel que $P\big( T\leqslant T_0\big)=0,9$. A la calculatrice, nous obtenons \[P\big( T\leqslant 18,5379\big)=0,9\] Ce qui signifie qu'il a une probabilité de $0,9$ de mettre moins de 18 minutes et 30 secondes (environ). Il peut donc partir au plus tard à 8 heures moins 18 minutes et 30 secondes, soit à 7 h 41 minutes et 30 secondes. à une minute près, il peut partir au maximum à 7 h 41,
   de sorte à avoir une probabilité d'arriver à l'heure de $ 0,9 $

Partie C : le bus

Lorsque l'élève utilise le bus, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par une variable aléatoire $T'$ qui suit la loi normale d'espérance $\mu' = 15$ et d'écart-type $\sigma'$.

On sait que la probabilité qu'il mette plus de 20 minutes pour se rendre à son lycée en bus est de $0,05$. On note $Z'$ la variable aléatoire égale à $\dfrac{T'-15}{\sigma'}$

1. Quelle loi la variable aléatoire $Z'$ suit-elle ?
D'après le cours $Z'$ suit une loi normale centrée-réduite.
2. Déterminer une valeur approchée à $0,01$ près de l'écart-type $\sigma'$ de la variable aléatoire $T'$.
Puisque $P\big(T' \geqslant 20\big)= 0,05$, il vient \[ P\Big(\dfrac{T'- 15}{\sigma'} \geqslant \dfrac{20-15}{\sigma'}\Big)= 0,05 \Leftrightarrow P\Big(Z' \geqslant \dfrac{5}{\sigma'}\Big)=0,05\] À la calculatrice, en considérant une loi normale centrée-réduite $Z'$, on trouve que \[ P\Big(Z'\geqslant 1,6449\Big)=0,05\] D'où \[\dfrac{5}{\sigma'}=1,6449 \] et donc \[\sigma'=\dfrac{5}{1,6449}=3,04\quad\text{ à }\quad 0,01\quad \text{près} \]

Exercice 2 5 points

Commun à tous les candidats

Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier chaque réponse. Une réponse non justifiée ne sera pas prise en compte On se place dans l'espace muni d'un repère orthonormé. On considère le plan $\mathcal{P}$ d'équation $x - y + 3z + 1 = 0$ et la droite $\mathcal{D}$ dont une représentation paramétrique est $\begin{cases} x=2t\\ y=1+t\quad,\quad t\in\mathbb{R} \\ z=-5+3t \end{cases}$ On donne les points $A(1~;~1;~0),\;B(3~;0~;~-1)$ et $C(7~;1~;~-2)$

1. Proposition 1 :
   Une représentation paramétrique de la droite $(AB)$ est $\begin{cases} x=5-2t\\ y=-1+t\quad,\quad t\in\mathbb{R} \\ z=-2+t \end{cases}$
2. Proposition 2 :
   Les droites $\mathcal{D}$ et $(AB)$ sont orthogonales.
3. Proposition 3 :
   Les droites $\mathcal{D}$ et $(AB)$ sont coplanaires.
4. Proposition 4 :
   La droite $\mathcal{D}$ coupe le plan $\mathcal{P}$ au point $E$ de coordonnées $(8;~-3;~-4)$.
5. Proposition 5 :
   Les plans $\mathcal{P}$ et $(ABC)$ sont parallèles.

Correction de l'exercice 2 (5 points)

Commun à tous les candidats

Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier chaque réponse. Une réponse non justifiée ne sera pas prise en compte On se place dans l'espace muni d'un repère orthonormé.
On considère le plan $\mathcal{P}$ d'équation $x - y + 3z + 1 = 0$ et la droite $\mathcal{D}$ dont une représentation paramétrique est $\begin{cases} x=2t\\ y=1+t\quad,\quad t\in\mathbb{R} \\ z=-5+3t \end{cases}$ On donne les points $A(1~;~1;~0),\;B(3~;0~;~-1)$ et $C(7~;1~;~-2)$

1. Proposition 1 :
   Une représentation paramétrique de la droite $(AB)$ est $\begin{cases} x=5-2t\\ y=-1+t\quad,\quad t\in\mathbb{R} \\ z=-2+t \end{cases}$
Vraie .

 

Il suffit de vérifier que les coordonnées des deux points A et B vérifient le système formé des trois équations paramétriques. Pour $t=2$ on retrouve les coordonnées du point A, et pour $t=1$ celles du point B.
1. Proposition 2 :
   Les droites $\mathcal{D}$ et $(AB)$ sont orthogonales.
Vraie .

 

$\mathcal{D}$ est dirigée par $\vec{d}$ de coordonnées $(2,~1,~3)$ et $(AB)$ par $\vec{AB}$ de coordonnées $(-2,~1,~1)$. Or $\vec{AB}\cdot \vec{d}= -4+1+3=0$, les vecteurs $\vec{AB}$ et $\vec{d}$ sont donc orthogonaux, les droites $\mathcal{D}$ et $(AB)$ sont donc orthogonales.
1. Proposition 3 :
   Les droites $\mathcal{D}$ et $(AB)$ sont coplanaires.
Fausse

 

Pour savoir si ces deux droites sont coplanaires, il suffit de savoir si elles sont sécantes, car étant orthogonales elles ne pourront pas être parallèles.

 

Pour cela on résout le système \[\begin{cases} 2t\hspace{0.7cm}=\;5-2t'&\quad(1)\\ 1+t\hspace{0.4cm}=\;-1+t'&\quad(2)\\ -5+3t=\;-2+t'&\quad(3) \end{cases}\]

 

En soustrayant membre à membre (3) et (2), il vient $2t-6=-1$ soit $t=\dfrac52$. On remplace dans (2): $t'=-2+t=-2+\dfrac52=\dfrac12$.

 

On vérifie dans (1): $2t=5$, alors que $5-2t'=5-1=4$. Ce qui signifie que ce système n'a pas de solution.

 

Puisque ces deux droites sont orthogonales et non sécantes, elles seront donc non coplanaires.
1. Proposition 4 :
   La droite $\mathcal{D}$ coupe le plan $\mathcal{P}$ au point $E$ de coordonnées $(8;~-3;~-4)$.
Fausse

 

On vérifie facilement que $E\in\mathcal{P}$, mais $E\notin\mathcal{D}$.

 

En effet, si on résout le système \[\begin{cases} 8=2t\\ -3=1+t\\ -4=-5+3t \end{cases}\]

 

On trouve que $t=4$ dans la première équation, valeur qui ne convient pas dans la seconde équation.
1. Proposition 5 :
   Les plans $\mathcal{P}$ et $(ABC)$ sont parallèles.
Vraie .

 

Le vecteur $\vec{n}$ de coordonnées $(1,~-1,~3)$ est un vecteur normal au plan $\mathcal{P}$.

 

Les vecteurs $\vec{AB}$ et $\vec{AC}$ ont pour coordonnées respectives $(2,~-1,~-1)$ et $(6,~0,~-2)$,

 

d'où \[\vec{n}\cdot\vec{AB}=2+1-3=0\quad\text{et}\quad \vec{n}\cdot\vec{AC}=6+0-6=0 \] $\vec{n}$ est donc normal au plan $(ABC)$.

 

$\mathcal{P}$ et $(ABC)$ ayant un vecteur normal commun sont donc parallèles.

Exercice 3 5 points

Fonctions

Soit $f$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par \[f(x) = x\,\mathrm{e}^{-x}.\] On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthogonal.

Partie A

1. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0;~+\infty[$. Pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, calculer $f'(x)$. En déduire les variations de la fonction $f$ sur l'intervalle $[0~;~+\infty[$.
2. Déterminer la limite de la fonction $f$ en $+\infty$. Quelle interprétation graphique peut-on faire de ce résultat?

Partie B

Soit $\mathcal{A}$ la fonction définie sur l'intervalle $[0;~+\infty[$ de la façon suivante :
pour tout réel $t$ de l'intervalle $[0~;~+\infty[\,,\,\mathcal{A}(t)$ est l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe $\mathcal{C}$ et les droites d'équations $x = 0$ et $x = t$.

1. Déterminer le sens de variation de la fonction $\mathcal{A}$.
2. On admet que l'aire du domaine délimité par la courbe $\mathcal{C}$ et l'axe des abscisses est égale à 1 unité d'aire. Que peut-on en déduire pour la fonction $\mathcal{A}$?
3. On cherche à prouver l'existence d'un nombre réel $\alpha$ tel que la droite d'équation $x =\alpha$ partage le domaine compris entre l'axe des abscisses et la courbe $\mathcal{C}$, en deux parties de même aire, et à trouver une valeur approchée de ce réel.
   1. Démontrer que l'équation $\mathcal{A}(t)=\dfrac12$ admet une unique solution sur l'intervalle $[0~;~+\infty[$
   2. Sur le graphique fourni en annexe à rendre avec la copie sont tracées la courbe $\mathcal{C}$, ainsi que la courbe $\Gamma$ représentant la fonction $\mathcal{A}$.
      Sur le graphique de l' annexe, identifier les courbes $\mathcal{C}$ et $\Gamma$, puis tracer la droite d'équation $y=\dfrac12$. En déduire une valeur approchée du réel $\alpha$.
      Hachurer le domaine correspondant à $\mathcal{A}(\alpha)$.
4. On définit la fonction $g$ sur l'intervalle $[0;~+\infty[$ par $g(x) = (x+1)\,\mathrm{e}^{-x}$.
   1. On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0;~+\infty[$.
   Pour tout réel $x$ de l'intervalle $[0;~+\infty[$, calculer $g'(x)$.
   2. En déduire, pour tout réel $t$ de l'intervalle $[0;~+\infty[$, une expression de $\mathcal{A}(t)$.
   3. Calculer une valeur approchée à $10^{-2}$ près de $\mathcal{A}(6)$.

 Annexe :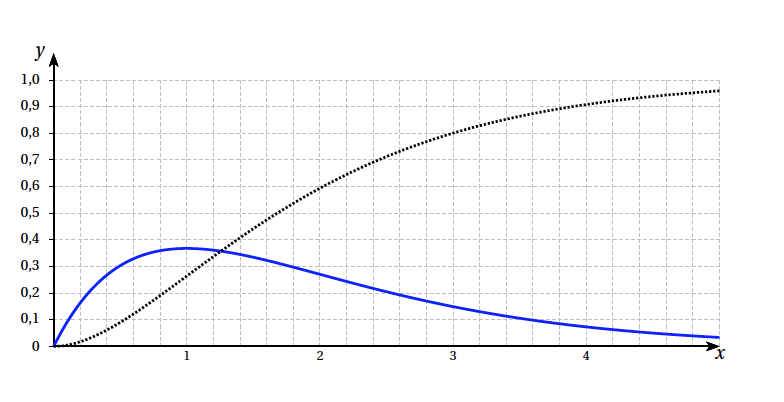

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Fonctions

Soit $f$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par \[f(x) = x\,\mathrm{e}^{-x}.\] On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthogonal.

Partie A

1. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0;~+\infty[$. Pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, calculer $f'(x)$. En déduire les variations de la fonction $f$ sur l'intervalle $[0~;~+\infty[$.
$f'(x)=\mathrm{e}^{-x}-x\mathrm{e}^{-x}=(1 - x)\mathrm{e}^{-x}$ $\mathrm{e}^{-x}$ étant toujours strictement positif, $f'(x)$ sera du signe de $1-x$. Il s'ensuit que \[f'(x)\geqslant0\quad \text{ sur }\quad [0,~1]\quad \text{ et }\quad f'(x)<0\quad \text{ sur }\quad ]1,~+\infty[\] $f$ est donc croissante sur $[0,~1]$ et décroissante sur $]1,~+\infty[$.
2. Déterminer la limite de la fonction $f$ en $+\infty$. Quelle interprétation graphique peut-on faire de ce résultat?
On sait que $\lim\limits_{x\rightarrow +\infty} x\,\mathrm{e}^{-x}=0$, ce qui signifie que l'axe des abscisses est une asymptote horizontale à la courbe $\mathcal{C}$

Partie B

Soit $\mathcal{A}$ la fonction définie sur l'intervalle $[0;~+\infty[$ de la façon suivante :
pour tout réel $t$ de l'intervalle $[0~;~+\infty[\,,\,\mathcal{A}(t)$ est l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe $\mathcal{C}$ et les droites d'équations $x = 0$ et $x = t$.

1. Déterminer le sens de variation de la fonction $\mathcal{A}$.
Comme la fonction $f$ est continue et positive sur l'intervalle $[0;~+\infty[$ alors \[\mathcal{A}(t)=\int_0^t f(x)\,\mathrm{d}x\]et donc, pour tout $t\in [0;~+\infty[\quad \mathcal{A}'(t)=f(t)$ Comme $f$ est positive sur l'intervalle $[0~;~+\infty[$ il s'ensuit que la fonction $\mathcal{A}$ est croissante sur $[0~;~+\infty[$.
2. On admet que l'aire du domaine délimité par la courbe $\mathcal{C}$ et l'axe des abscisses est égale à 1 unité d'aire. Que peut-on en déduire pour la fonction $\mathcal{A}$?
On peut en déduire que la fonction $\mathcal{A}$ a pour limite 1 en $+\infty$.
3. On cherche à prouver l'existence d'un nombre réel $\alpha$ tel que la droite d'équation $x =\alpha$ partage le domaine compris entre l'axe des abscisses et la courbe $\mathcal{C}$, en deux parties de même aire, et à trouver une valeur approchée de ce réel.
   1. Démontrer que l'équation $\mathcal{A}(t)=\dfrac12$ admet une unique solution sur l'intervalle $[0~;~+\infty[$
   Dressons le tableau de variations de la fonction $\mathcal{A}$ sur $[0~;~+\infty[$ :
   
   
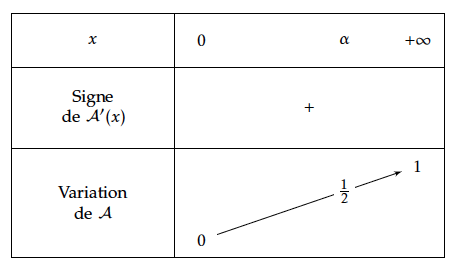
   1. Sur le graphique fourni en annexe à rendre avec la copie sont tracées la courbe $\mathcal{C}$, ainsi que la courbe $\Gamma$ représentant la fonction $\mathcal{A}$.
      Sur le graphique de l' annexe, identifier les courbes $\mathcal{C}$ et $\Gamma$, puis tracer la droite d'équation $y=\dfrac12$. En déduire une valeur approchée du réel $\alpha$.
   
   
   Hachurer le domaine correspondant à $\mathcal{A}(\alpha)$.

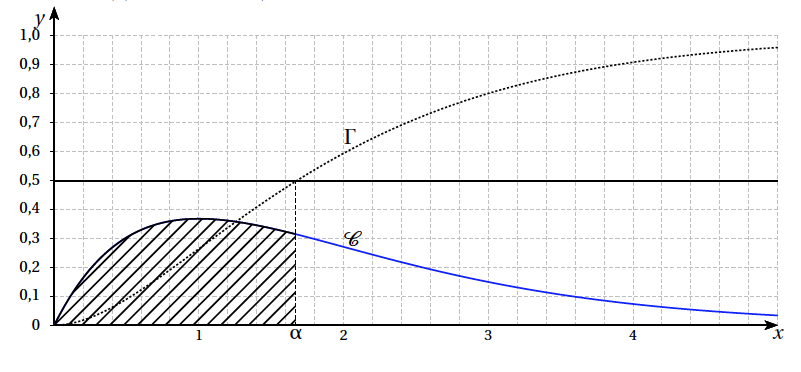
• On définit la fonction $g$ sur l'intervalle $[0;~+\infty[$ par $g(x) = (x+1)\,\mathrm{e}^{-x}$.
  1. On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0;~+\infty[$.
  Pour tout réel $x$ de l'intervalle $[0;~+\infty[$, calculer $g'(x)$.

$g'(x)= \mathrm{e}^{-x}-(x+1)\mathrm{e}^{-x}=-x\,\mathrm{e}^{-x}$

• En déduire, pour tout réel $t$ de l'intervalle $[0;~+\infty[$, une expression de $\mathcal{A}(t)$.

On remarque que $g'(x)= -f(x)$, d'où \[\mathcal{A}(t)=\int_0^t f(x)\,\mathrm{d}x =\int_0^t -g'(x)\,\mathrm{d}x=\left[-g(x)\right]_0^t = -g(t)+g(0)=1-(1+t)\mathrm{e}^{-t}\]

• Calculer une valeur approchée à $10^{-2}$ près de $\mathcal{A}(6)$.

$\mathcal{A}(6)=1-7\mathrm{e}^{-6}\simeq 0,98$

 

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère la suite de nombres complexes $\left(z_n\right)$ définie par $z_0=\sqrt{3}-\mathrm{i}$ et pour tout entier naturel $n$: \[z_{n+1} = (1+\mathrm{i})z_n.\]
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Pour tout entier naturel $n$, on pose $u_n = \left|z_{n}\right|$.

1. Calculer $u_0$.
2. Démontrer que $\left(u_n\right)$ est la suite géométrique de raison $\sqrt{2}$ et de premier terme 2.
3. Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$.
4. Déterminer la limite de la suite $\left(u_n\right)$.
5. Étant donné un réel positif $p$, on souhaite déterminer, à l'aide d'un algorithme, la plus petite valeur de l'entier naturel $n$ telle que $u_n > p$. Recopier l'algorithme ci-dessous et le compléter par les instructions de traitement et de sortie, de façon à afficher la valeur cherchée de l'entier $n$. $$\begin{array}{|lcl|} \hline\text{Variables}&: &u \text{ est un réel}\\ &&p \text{ est un réel}\\ && n \text{ est un entier}\\ \text{Initialisation}&:& \text{Affecter à  } n \text{la valeur 0}\\ && \text{Affecter à  } u \text{la valeur 2}\\ \text{Entrée}&:& \text{Demander la valeur de } p \\ \text{Traitement}&:&\\ && \\ && \\ &&\\ \text{Sortie}&:& \\ \hline \end{array}$$

Partie B

1. Déterminer la forme algébrique de $z_1$.
2. Déterminer la forme exponentielle de $z_0$ et de $1+\mathrm{i}$. En déduire la forme exponentielle de $z_1$.
3. Déduire des questions précédentes la valeur exacte de $\cos\left(\dfrac{\pi}{12}\right)$

 

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère la suite de nombres complexes $\left(z_n\right)$ définie par $z_0=\sqrt{3}-\mathrm{i}$ et pour tout entier naturel $n$: \[z_{n+1} = (1+\mathrm{i})z_n.\]
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Pour tout entier naturel $n$, on pose $u_n = \left|z_{n}\right|$.

1. Calculer $u_0$.
$u_0=\vert z_0 \vert= \left\vert \sqrt3-\mathrm{i}\right\vert = 2$.
2. Démontrer que $\left(u_n\right)$ est la suite géométrique de raison $\sqrt{2}$ et de premier terme 2.
$u_{n+1}= \left\vert z_{n+1}\right\vert= \left\vert (1+\mathrm{i})z_n\right\vert= \vert 1+\mathrm{i}\vert \times \vert z_n \vert=\sqrt2\vert z_n \vert=\sqrt2 u_n $
3. Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$.
D'après le cours, pour tout entier naturel $n$, on a $u_n = 2\left(\sqrt2\right)^n$ ; $(u_n)$ est la suite géométrique de raison $\sqrt{2}$ et de premier terme $u_0=2$.
4. Déterminer la limite de la suite $\left(u_n\right)$.
$(u_n)$ est une suite géométrique de raison $\sqrt2>1$ et de premier terme strictement positif, elle diverge donc vers $+\infty$.
5. Étant donné un réel positif $p$, on souhaite déterminer, à l'aide d'un algorithme, la plus petite valeur de l'entier naturel $n$ telle que $u_n > p$. Recopier l'algorithme ci-dessous et le compléter par les instructions de traitement et de sortie, de façon à afficher la valeur cherchée de l'entier $n$. $$\begin{array}{|lcl|}\hline \text{Variables}&: &u \text{ est un réel}\\ &&p \text{ est un réel}\\ && n \text{ est un entier}\\ \text{Initialisation}&:& \text{Affecter à  } n \text{la valeur 0}\\ && \text{Affecter à  } u \text{la valeur 2}\\ \text{Entrée}&:& \text{Demander la valeur de  } p \\ \text{Traitement}&:& \text{Tant que } u \leqslant p \text{ Faire }\\ && \text{Affecter à  } n \text{ la valeur } n+1\\ && \text{Affecter à } u \text{ la valeur } \sqrt2\times u\\ && \text{ Fin du Tant Que }\\ \text{Sortie}&:& \text{ Afficher } n\\ \hline \end{array}$$

Partie B

1. Déterminer la forme algébrique de $z_1$.
$z_1 = (1+\mathrm{i})\times (\sqrt3-\mathrm{i})= 1+\sqrt3 + \mathrm{i}(\sqrt3-1)$.
2. Déterminer la forme exponentielle de $z_0$ et de $1+\mathrm{i}$. En déduire la forme exponentielle de $z_1$.
$z_0 = 2\left(\dfrac{\sqrt3}{2}-\dfrac12\mathrm{i}\right) = 2\mathrm{e}^{-\mathrm{i}\frac{\pi}{6}}$

 

$1+\mathrm{i}=\sqrt2\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}$.

 

$z_1= 2\mathrm{e}^{-\mathrm{i}\frac{\pi}{6}} \times \sqrt2\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}=2\sqrt2\mathrm{e}^{\mathrm{i}\frac{\pi}{12}}$.
1. Déduire des questions précédentes la valeur exacte de $\cos\left(\dfrac{\pi}{12}\right)$
Des deux questions précédentes, on obtient que \[1+\sqrt3 + \mathrm{i}(\sqrt3-1)=2\sqrt2\mathrm{e}^{\mathrm{i}\frac{\pi}{12}}= 2\sqrt2 \Big(\cos\left(\dfrac{\pi}{12}\right)+\mathrm{i}\sin\left(\dfrac{\pi}{12}\right)\Big) \]

 

D'où \[\cos\left(\dfrac{\pi}{12}\right)= \dfrac{1+\sqrt3}{2\sqrt2}=\dfrac{\sqrt2+\sqrt6}{4}\]

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Un laboratoire étudie la propagation d'une maladie sur une population.

Unindividu sain est un individu n'ayant jamais été touché par la maladie.

Unindividu malade est un individu qui a été touché par la maladie et non guéri.

Unindividu guéri est un individu qui a été touché par la maladie et qui a guéri.

Une fois guéri, un individu est immunisé et ne peut plus tomber malade.

Les premières observations nous montrent que, d'un jour au jour suivant:

• $5\,\%$ des individus tombent malades;
• $20\,\%$ des individus guérissent.

Pour tout entier naturel $n$, on note $a_n$ la proportion d'individus sains $n$ jours après le début de l'expérience, $b_n$ la proportion d'individus malades $n$ jours après le début de l'expérience, et $c_n$ celle d'individus guéris $n$ jours après le début de l'expérience. On suppose qu'au début de l'expérience, tous les individus sont sains, c'est à dire que $a_0=1$, $b_0 = 0$ et $c_0 = 0$

1. Calculer $a_1$, $b_1$ et $c_1$.
2. 1. Quelle est la proportion d'individus sains qui restent sains d'un jour au jour suivant ? En déduire $a_{n+1}$ en fonction de $a_n$.
   2. Exprimer $b_{n+1}$ en fonction de $a_n$ et de $b_n$.
On admet que $c_{n+1} = 0,2b_n + c_n$. Pour tout entier naturel $n$, on définit $U_n=\begin{pmatrix} a_n\\b_n\\c_n \end{pmatrix}$ On définit les matrices $A=\begin{pmatrix} 0,95&0&0\\ 0,05&0,8&0\\ 0&0,2&1 \end{pmatrix}$ et $D=\begin{pmatrix} 0,95&0&0\\ 0&0,8&0\\ 0&0&1 \end{pmatrix}$ On admet qu'il existe une matrice inversible $P$ telle que $D=P^{-1}\times A\times P$ et que, pour tout entier naturel $n$ supérieur ou égal à 1, $A^n=P\times D^{n}\times P^{-1}$.
3. 1. Vérifier que, pour tout entier naturel $n$, $U_{n+1}= A\times U_n$. On admet que, pour tout entier naturel $n$, $U_n=A^n\times U_0$.
   2. Démontrer par récurrence que, pour tout entier naturel $n$ non nul, $D^n=\begin{pmatrix} 0,95^n&0&0\\ 0&0,8^n&0\\ 0&0&1 \end{pmatrix}$
On admet que $A^n =\begin{pmatrix} 0,95^n&0&0\\ \dfrac13\left(0,95^n-0,8^n\right)&0,8^n&0\\ \dfrac13\left(3-4\times0,95^n+0,8^n\right)&1-0,8^n&1 \end{pmatrix}$
4. 1. Vérifier que pour tout entier naturel $n$, $b_n=\dfrac13\left(0,95^n-0,8^n\right)$
   2. Déterminer la limite de la suite $\left(b_n\right)$.
   3. On admet que la proportion d'individus malades croût pendant plusieurs jours, puis décroit.
      On souhaite déterminer le pic épidémique, c'est à dire le moment où la proportion d'individus malades est à son maximum.
      A cet effet, on utilise l'algorithme donné en  annexe 2  à rendre avec la copie, dans lequel on compare les termes successifs de la suite $(b_n)$.
      Compléter l'algorithme de façon qu'il affiche le rang du jour où le pic épidémique est atteint et compléter le tableau fourni en annexe 2.
      Conclure.

Annexe : $$\begin{array}{|ll cl|} \hline \text{Variables}&: &b,~b',~x,~y \text{ sont des réels}&\\ && k \text{ est un entier naturel}&\\ && n \text{ est un entier }&\\ \text{Initialisation}&:& \text{ Affecter à } b \text{ la valeur 0}&\\ && \text{ Affecter à } b'\text{ la valeur 0,05}&\\ && \text{ Affecter à } k \text{ la valeur 0 }&\\ && \text{Affecter à } x \text{ la valeur 0,95}&\\ && \text{ Affecter à } y \text{ la valeur 0,8}&\\ \text{Traitement}&:& \text{ Tant que } b < b' \text{ faire: }&\\ &&\quad\vert \text{ Affecter à } k \text{ la valeur } k+1&\\ &&\quad\vert \text{ Affecter à } b \text{ la valeur } b'&\\ &&\quad\vert \text{ Affecter à } x \text{ la valeur } 0,95 x&\\ &&\quad\vert \text{ Affecter à } y \text{ la valeur } 0,80 y&\\ &&\quad\vert \text{ Affecter à } b' \text{ la valeur } \ldots \ldots&\\ &&\text{ Fin Tant que}&\\ \text{Sortie}&:& \text{ Afficher } \ldots \ldots & \\ \hline\end{array}$$

 

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Un laboratoire étudie la propagation d'une maladie sur une population.

Unindividu sain est un individu n'ayant jamais été touché par la maladie.

Unindividu malade est un individu qui a été touché par la maladie et non guéri.

Unindividu guéri est un individu qui a été touché par la maladie et qui a guéri.

Une fois guéri, un individu est immunisé et ne peut plus tomber malade.

Les premières observations nous montrent que, d'un jour au jour suivant:

• $5\,\%$ des individus tombent malades;
• $20\,\%$ des individus guérissent.

Pour tout entier naturel $n$, on note $a_n$ la proportion d'individus sains $n$ jours après le début de l'expérience, $b_n$ la proportion d'individus malades $n$ jours après le début de l'expérience, et $c_n$ celle d'individus guéris $n$ jours après le début de l'expérience. On suppose qu'au début de l'expérience, tous les individus sont sains, c'est à dire que $a_0=1$, $b_0 = 0$ et $c_0 = 0$

1. Calculer $a_1$, $b_1$ et $c_1$.

 

$a_1=0,95$, $b_1=0,05$ et $c_1=0$.
1. 1. Quelle est la proportion d'individus sains qui restent sains d'un jour au jour suivant ? En déduire $a_{n+1}$ en fonction de $a_n$.
   
   
   $95\%$ des individus restent sains d'un jour au jour suivant d'où $$a_{n+1}=0,95a_n$$
   1. Exprimer $b_{n+1}$ en fonction de $a_n$ et de $b_n$.
   
   
   Au jour $n+1$, $5\%$ des individus sains ($a_n$) deviennent malades (soit $0,05a_n$) et $80\%$ des individus malades $b_n$ le reste ($0,8b_n$), d'où \[b_{n+1}=0,05a_n + 0,8b_n\]
On admet que $c_{n+1} = 0,2b_n + c_n$. Pour tout entier naturel $n$, on définit $U_n=\begin{pmatrix} a_n\\b_n\\c_n \end{pmatrix}$ On définit les matrices $A=\begin{pmatrix} 0,95&0&0\\ 0,05&0,8&0\\ 0&0,2&1 \end{pmatrix}$ et $D=\begin{pmatrix} 0,95&0&0\\ 0&0,8&0\\ 0&0&1 \end{pmatrix}$ On admet qu'il existe une matrice inversible $P$ telle que $D=P^{-1}\times A\times P$ et que, pour tout entier naturel $n$ supérieur ou égal à 1, $A^n=P\times D^{n}\times P^{-1}$.
2. 1. Vérifier que, pour tout entier naturel $n$, $U_{n+1}= A\times U_n$. On admet que, pour tout entier naturel $n$, $U_n=A^n\times U_0$.
   
   
   Pour tout entier naturel $n$, \[A\times U_n=\begin{pmatrix} 0,95&0&0\\ 0,05&0,8&0\\ 0&0,2&1 \end{pmatrix}\times\begin{pmatrix} a_n\\b_n\\c_n \end{pmatrix}=\begin{pmatrix} 0,95a_n\\ 0,05a_n+0,8b_n\\0,2b_n+c_n \end{pmatrix}=U_{n+1} \]
   1. Démontrer par récurrence que, pour tout entier naturel $n$ non nul, $D^n=\begin{pmatrix} 0,95^n&0&0\\ 0&0,8^n&0\\ 0&0&1 \end{pmatrix}$
   
   
   C'est vrai pour $n=0$ car $D^{0}=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix}$ Supposons que $D^n=\begin{pmatrix} 0,95^n&0&0\\ 0&0,8^n&0\\ 0&0&1 \end{pmatrix}$ alors: \[D^{n+1}=D\times D^n=\begin{pmatrix} 0,95&0&0\\ 0&0,8&0\\ 0&0&1 \end{pmatrix} \times \begin{pmatrix} 0,95^n&0&0\\ 0&0,8^n&0\\ 0&0&1 \end{pmatrix} = \begin{pmatrix} 0,95^{n+1}&0&0\\ 0&0,8^{n+1}&0\\ 0&0&1 \end{pmatrix} \] C'est donc vrai au rang $n+1$ Par récurrence, cela sera vrai pour tout entier naturel $n$.
On admet que $A^n =\begin{pmatrix} 0,95^n&0&0\\ \dfrac13\left(0,95^n-0,8^n\right)&0,8^n&0\\ \dfrac13\left(3-4\times0,95^n+0,8^n\right)&1-0,8^n&1 \end{pmatrix}$
3. 1. Vérifier que pour tout entier naturel $n$, $b_n=\dfrac13\left(0,95^n-0,8^n\right)$
   $U_n=A^n\times U_0 $, Soit \[\begin{pmatrix} a_n\\b_n\\c_n \end{pmatrix}=\begin{pmatrix} 0,95^n&0&0\\ \dfrac13\left(0,95^n-0,8^n\right)&0,8^n&0\\ \dfrac13\left(3-4\times0,95^n+0,8^n\right)&1-0,8^n&1 \end{pmatrix}\times \begin{pmatrix} 1\\0\\0 \end{pmatrix}= \begin{pmatrix} 0,95^n\\ \dfrac13\left(0,95^n-0,8^n\right)\\ \dfrac13\left(3-4\times0,95^n+0,8^n\right) \end{pmatrix} \] d'où \[b_n=\dfrac13\left(0,95^n-0,8^n\right)\]
   2. Déterminer la limite de la suite $\left(b_n\right)$.
   
   
   $(b_n)$ est la somme de deux suites géométriques de raisons comprises entre 0 et 1 qui convergent vers 0, il en est donc de même de $(b_n)$.
   1. On admet que la proportion d'individus malades croût pendant plusieurs jours, puis décroit.
      On souhaite déterminer le pic épidémique, c'est à dire le moment où la proportion d'individus malades est à son maximum.
      A cet effet, on utilise l'algorithme donné en  annexe 2  à rendre avec la copie, dans lequel on compare les termes successifs de la suite $(b_n)$.
      Compléter l'algorithme de façon qu'il affiche le rang du jour où le pic épidémique est atteint et compléter le tableau fourni en annexe 2.
      Conclure.
   
   
   $$\begin{array}{|ll cl|} \hline \text{Variables}&: &b,~b',~x,~y \text{ sont des réels}&\\ && k \text{ est un entier naturel}&\\ && n \text{ est un entier }&\\ \text{Initialisation}&:& \text{ Affecter à } b \text{ la valeur 0}&\\ && \text{ Affecter à } b'\text{ la valeur 0,05}&\\ && \text{ Affecter à } k \text{ la valeur 0 }&\\ && \text{Affecter à } x \text{ la valeur 0,95}&\\ && \text{ Affecter à } y \text{ la valeur 0,8}&\\ \text{Traitement}&:& \text{ Tant que } b < b' \text{ faire: }&\\ &&\quad\vert \text{ Affecter à } k \text{ la valeur } k+1&\\ &&\quad\vert \text{ Affecter à } b \text{ la valeur } b'&\\ &&\quad\vert \text{ Affecter à } x \text{ la valeur } 0,95 x&\\ &&\quad\vert \text{ Affecter à } y \text{ la valeur } 0,80 y&\\ &&\quad\vert \text{ Affecter à } b' \text{ la valeur } \dfrac13(x-y)&\\ &&\text{ Fin Tant que}&\\ \text{Sortie}&:& \text{ Afficher }k& \\ \hline\end{array}$$
   
   
   $$\begin{array}{|c|c|c|c|c|c|} \hline & k & b & x & y & b' & Test: b < b' ?\\ \hline \hline \text{Après le 7e passage dans la boucle Tant que }& 7 & 0,1628 & 0,6634 & 0,1678 & 0,1652 & \text{Vrai}\\ \hline \text{Après le 8e passage éventuel dans la boucle Tant que} & 8 & 0,1652& 0,6302 & 0,1342 & 0,1653 & \text{Vrai}\\ \hline \text{Après le 9e passage éventuel dans la boucle Tant que }& 9 & 0,1653 &0,5987 & 0,1073 &0,1637 & \text{Faux}\\ \hline \end{array} $$ Pour chaque ligne du tableau, $b$ désigne $b_k$ et $ b'$ désigne $b_{k+1}$; on a donc : $$\begin{array}{|c|c|c|c|c|} \hline k & 7 & 8 & 9 & 10 \\ \hline b_{k} & 0,1628 & 0,1652 & 0,1653 & 0,1637 \\ \hline \end{array} $$ Le rang du jour où le pic épidémique est atteint est donc le 9.