Baccalauréat S Liban 27 mai 2015 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (5 points)
ABCDEFGH est un cube. 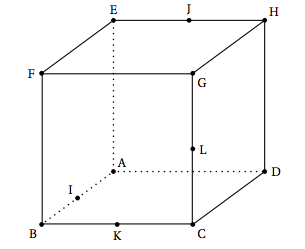
I est le milieu du segment [AB], J est le milieu du segment [EH], K est le milieu du segment [BC] et L est le milieu du segment [CG]. On munit l'espace du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
-
- Démontrer que la droite (FD) est orthogonale au plan (IJK). Déterminons tout d’abord les coordonnées de quelques points :
- En déduire une équation cartésienne du plan (IJK). Une équation du plan $(IJK)$ est donc de la forme :
$I(0,5;0;0)$, $J(0;0,5;1)$, $K(1;0,5;0)$, $F(1;0;1)$ et $D(0;1;0)$
Ainsi $\vec{IJ}(-0,5;0,5;1)$, $\vec{IK}(0,5;0,5;0)$ et $\vec{DF}(1;-1;1)$.
Les vecteurs $\vec{IJ}$ et $\vec{IK}$ ne sont clairement pas colinéaires. Ils définissent donc bien le plan $(IJK)$.
$\vec{DF}.\vec{IJ} = -0,5 \times 1 + 0,5 \times (-1) + 1 \times 1 = 0$.
$\vec{DF}.\vec{IK} = 0,5 \times 1 + 0,5 \times (-1) + 0 \times 1 = 0$.
Ainsi le vecteur $\vec{DF}$ est orthogonal à deux vecteurs non colinéaires du plan $(IJK)$. C’est donc un vecteur normal de ce plan.
La droite $(DF)$ est bien orthogonale au plan $(IJK)$.
$\quad$
$$x-y+z+d=0$$
Le point $I(0,5;0;0)$ appartient au plan donc
$$0,5 + d =0 \iff d=-0,5$$
Une équation du plan $(IJK)$ est donc :
$$x-y+z-0,5 = 0$$ - Déterminer une représentation paramétrique de la droite (FD). En utilisant le point $F$ et le vecteur $\vec{DF}$ ont obtient la représentation paramétrique suivante de la droite $(DF)$ :
- Soit $M$ le point d'intersection de la droite (FD) et du plan (IJK). Déterminer les coordonnées du point $M$. Les coordonnées du point $M$ vérifient à la fois les équations de $(DF)$ et l’équation de $(IJK)$.
- Déterminer la nature du triangle IJK et calculer son aire. $IJ = \sqrt{(-0,5)^2+0,5^2+1^2} = \sqrt{1,5}$
- Calculer le volume du tétraèdre FIJK. $[MF]$ est la hauteur issue de $F$ du tétraèdre $FIJK$.
- Les droites (IJ) et (KL) sont-elles sécantes ?
$$\begin{cases} x=1 +t\\y=-t\\z=1+t \end{cases} \qquad t\in \mathbb R$$
$\quad$
On obtient ainsi :
$1+t – (-t)+1+t-0,5= 0 \iff 3t = -1,5 \iff t = -0,5$
On utilise cette valeur de $t$ dans les équations de $(DF)$ pour trouver les coordonnées de $M$ :
$$\begin{cases} x_M = 0,5\\y_M=0,5\\z_M=0,5 \end{cases}$$
$\quad$
$IK = \sqrt{0,5^2+0,5^2} = \sqrt{0,5}$
$KJ = \sqrt{(-1)^2+1^2} = \sqrt{2}$
Dans le triangle $IJK$ le plus grand côté est $KJ$.
Or $KJ^2 = 2$ et $IJ^2+IK^2 = 1,5+0,5=2$
Ainsi $KJ^2=IJ^2+IK^2$.
D’après la réciproque du théorème de Pythagore, le triangle $IJK$ est rectangle en $I$.
L’aire de $IJK$ est $\mathscr{A} = \dfrac{\sqrt{1,5} \times \sqrt{0,5}}{2}= \dfrac{\sqrt{0,75}}{2}$.
$MF^2=(1-0,5)^2+(-0,5)^2+(-0,5)^2 = 1,125$ ainsi $MF=\sqrt{0,75}$
Donc le volume de $FIJK$ est :
$$\mathscr{V} = \dfrac{1}{3}\times \text{Aire de la base}\times \text{Hauteur}=\dfrac{1}{3}\mathscr{B}h$$ $$\mathscr{V} = \dfrac{\sqrt{0,75}\times \sqrt{0,75}}{6} = \dfrac{0,75}{6} = \dfrac{1}{8}$$
On a $\vec{IJ}(-0,5;0,5;1)$ et $\vec{KL}(1;0,5;0)$.
Ces 2 vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.Regardons si les droites sont sécantes. Une représentation paramétrique de $(IJ)$ est $$\begin{cases}x=0,5 -0,5t\\y=0,5t\\z=t\end{cases} \qquad t\in\mathbb R$$
Une représentation paramétrique de $(KL)$ est $$\begin{cases} x=1\\y=0,5+0,5k\\z=0,5k\end{cases} \qquad k\in\mathbb R$$
Résolvons le système : $$\begin{align*} \begin{cases}0,5-0,5t=1\\0,5t=0,5+0,5k\\t=0,5k \end{cases} &\iff \begin{cases}t=-1\\-0,5=0,5+0,5k\\-1=0,5k \end{cases}\iff \begin{cases} t=-1\\k=-2\\k=-2 \end{cases} \end{align*}$$ Les deux droites sont donc sécantes en $P(1;-0,5;-1)$.
Remarque : On pouvait aussi vérifier que le point $L$ appartient bien au plan $(IJK)$.
- On obtient ainsi deux droites coplanaires non parallèles donc sécantes.
Une figure avec Geogebra
- Vues: 22217
