Baccalauréat S Polynésie 12 juin 2015
Exercice 1 3 points
On considère le pavé droit ABCDEFGH ci-dessous, pour lequel AB = 6, AD = 4 et AE = 2. I, J et K sont les points tels que $\vec{\text{AI}} = \dfrac{1}{6} \vec{\text{AB}},\:\: \vec{\text{AJ}} = \dfrac{1}{4} \vec{\text{AD}},\:\: \vec{\text{AK}} = \dfrac{1}{2} \vec{\text{AE}}$. 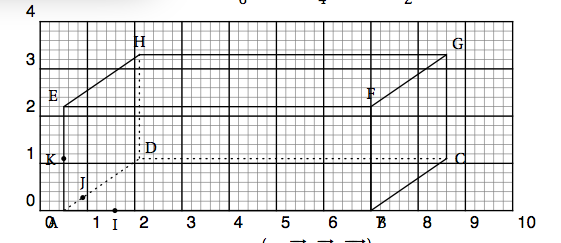
On se place dans le repère orthonormé $\left(\text{A}~;~ \vec{\text{AI}},~ \vec{\text{AJ}},~\vec{\text{AK}}\right)$.
- Vérifier que le vecteur $\vec{n}$ de coordonnées $\begin{pmatrix}2\\2\\- 9\end{pmatrix}$ est normal au plan (IJG).
- Déterminer une équation du plan (IJG).
- Déterminer les coordonnées du point d'intersection L du plan (IJG) et de la droite (BF).
- Tracer la section du pavé ABCDEFGH par le plan (IJG). Ce tracé sera réalisé sur la figure (donnée en annexe à rendre avec la copie) . On ne demande pas de justification.
Annexe 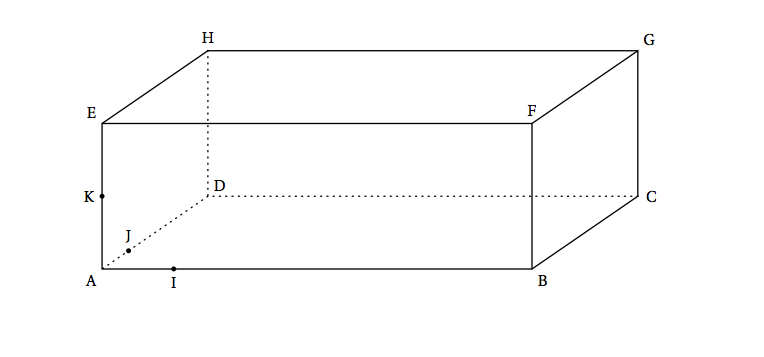
Correction de l'exercice 1 (3 points)
On considère le pavé droit ABCDEFGH ci-dessous, pour lequel AB = 6, AD = 4 et AE = 2. I, J et K sont les points tels que $\vec{\text{AI}} = \dfrac{1}{6} \vec{\text{AB}},\:\: \vec{\text{AJ}} = \dfrac{1}{4} \vec{\text{AD}},\:\: \vec{\text{AK}} = \dfrac{1}{2} \vec{\text{AE}}$. 
On se place dans le repère orthonormé $\left(\text{A}~;~ \vec{\text{AI}},~ \vec{\text{AJ}},~\vec{\text{AK}}\right)$.
- Vérifier que le vecteur $\vec{n}$ de coordonnées $\begin{pmatrix}2\\2\\- 9\end{pmatrix}$ est normal au plan (IJG). On a : $\vec{AB} = 6\vec{AI}$, $\vec{AD} = 4\vec{AJ}$ et $\vec{AE} = 2\vec{AK}$
- Déterminer une équation du plan (IJG). Une équation du plan $(IJG)$ est donc de la forme :
- Déterminer les coordonnées du point d'intersection L du plan (IJG) et de la droite (BF). On a $B(6;0;0)$ et $F(6;0;2)$.
- Tracer la section du pavé ABCDEFGH par le plan (IJG). Ce tracé sera réalisé sur la figure (donnée en annexe à rendre avec la copie) . On ne demande pas de justification.
On a donc les coordonnées suivantes :
$$I(1;0;0) \quad J(0;1;0) \quad G(6;4;2)$$
Ainsi $\vec{IJ}\begin{pmatrix} -1\\1\\0\end{pmatrix}$ et $\vec{IG} \begin{pmatrix} 5\\4\\2\end{pmatrix}$.
On constate que :
$\vec{n}.\vec{IJ} =2 \times (-1) + 2 \times 1 + 0 = 0$
$\vec{n}.\vec{IG} = 2 \times 5 + 2 \times 4 – 9 \times 2 = 0$
Ainsi, $\vec{n}$ est orthogonal à deux vecteurs non colinéaires du plan $(IJG)$. C’est donc un vecteur normal de ce plan.
$$2x+2y-9z+d=0$$.
Le point $I(1;0;0)$ appartient à ce plan. Ses coordonnées vérifient donc cette équation.
Par conséquent $2 + d = 0 \iff d=-2$.
Une équation du plan $(IJG)$ est donc : $$2x+2y-9z-2=0$$
Par conséquent $\vec{BF}\begin{pmatrix}0\\0\\2\end{pmatrix}$.
Ainsi une représentation paramétrique de la droite $(BF)$ est :
$$\begin{cases}x=6 \\\\y=0\\\\z=2t\end{cases} \qquad t \in \mathbb R$$
Les coordonnées du point $L$ vérifient à la fois l’équation du plan $(IJG)$ et celles de la droite $(BF)$.
Ainsi $2 \times 6-9\times 2t – 2 =0 \iff 10 = 18t \iff t = \dfrac{5}{9}$
$\quad$
On obtient ainsi $L\left(6;0;\dfrac{10}{9}\right)$.
Annexe 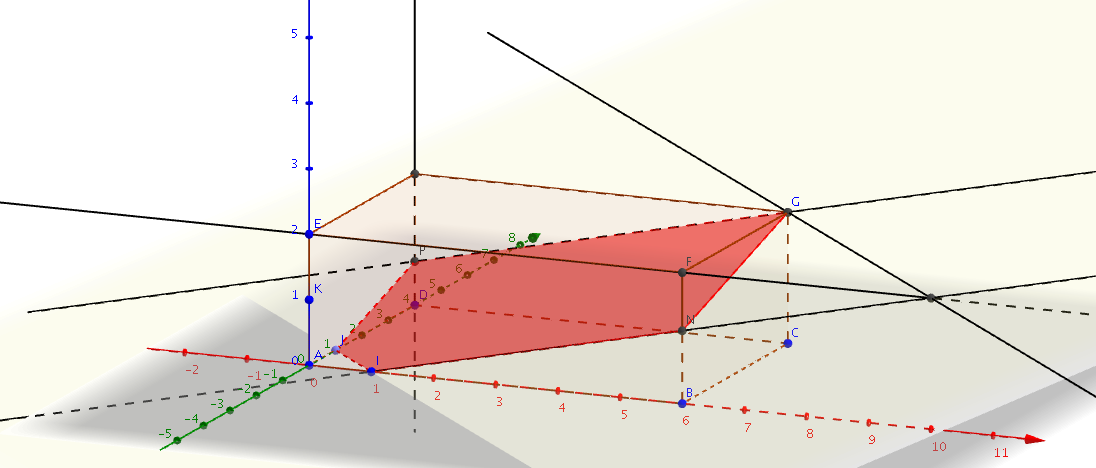
Une figure dynamique avec Geogebra :
Exercice 2 4 points
Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. À tout point $M$ d'affixe $z$ du plan, on associe le point $M'$ d'affixe $z'$ définie par: \[z' = z^2 + 4z + 3.\]
- Un point $M$ est dit invariant lorsqu'il est confondu avec le point $M'$ associé. Démontrer qu'il existe deux points invariants. Donner l'affixe de chacun de ces points sous forme algébrique, puis sous forme exponentielle.
- Soit A le point d'affixe $\dfrac{- 3 - \text{i}\sqrt{3}}{2}$ et B le point d'affixe $\dfrac{- 3 + \text{i}\sqrt{3}}{2}$. Montrer que OAB est un triangle équilatéral.
- Déterminer l'ensemble $\mathcal{E}$ des points $M$ d'affixe $z = x + \text{i}y$ où $x$ et $y$ sont réels, tels que le point $M'$ associé soit sur l'axe des réels.
- Dans le plan complexe, représenter les points A et B ainsi que l'ensemble $\mathcal{E}$.
Correction de l'exercice 2 (4 points)
Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. À tout point $M$ d'affixe $z$ du plan, on associe le point $M'$ d'affixe $z'$ définie par: \[z' = z^2 + 4z + 3.\]
- Un point $M$ est dit invariant lorsqu'il est confondu avec le point $M'$ associé. Démontrer qu'il existe deux points invariants. Donner l'affixe de chacun de ces points sous forme algébrique, puis sous forme exponentielle. Un point invariant vérifie donc :
- Soit A le point d'affixe $\dfrac{- 3 - \text{i}\sqrt{3}}{2}$ et B le point d'affixe $\dfrac{- 3 + \text{i}\sqrt{3}}{2}$. Montrer que OAB est un triangle équilatéral. $OA = |z_1| = \sqrt{3} = |z_2| = OB$.
- Déterminer l'ensemble $\mathcal{E}$ des points $M$ d'affixe $z = x + \text{i}y$ où $x$ et $y$ sont réels, tels que le point $M'$ associé soit sur l'axe des réels. Soit $z=x+\text{i} y$ alors :
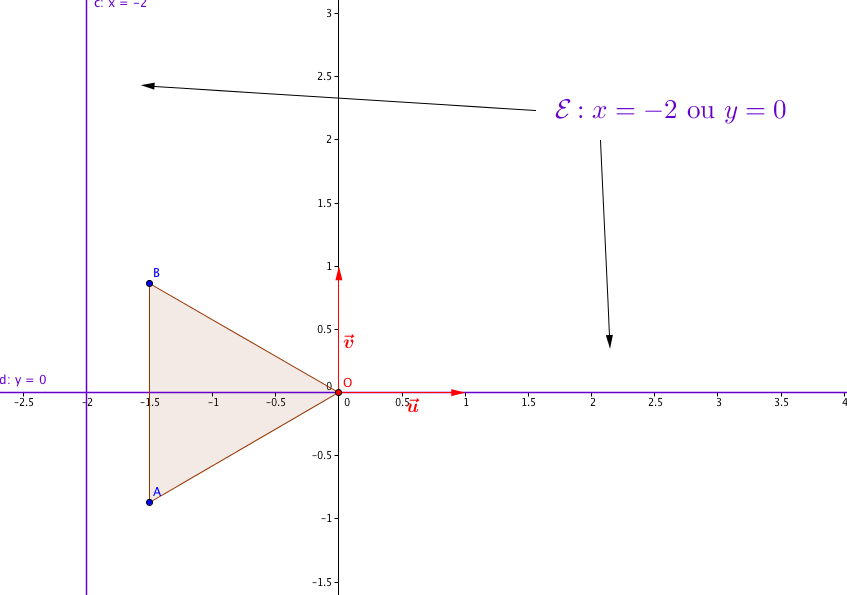
- Dans le plan complexe, représenter les points A et B ainsi que l'ensemble $\mathcal{E}$.
$z = z^2 +4z +3 \iff z^2 + 3z + 3=0$.
$\Delta = 3^2 – 4 \times 3 = -3<0$.
Cette équation possède donc deux solutions complexes :
$$z_1 = \dfrac{-3 -\text{i}\sqrt{3}}{2} \qquad z_2 = \dfrac{-3 +\text{i}\sqrt{3}}{2}$$
$|z_1| = \sqrt{\dfrac{(-3)^2 + 3}{2^2}} = \sqrt{3}$
Donc $z_1 = \sqrt{3} \left(-\dfrac{\sqrt{3}}{2} -\dfrac{\text{i}}{2}\right) = \sqrt{3}\text{e}^{7\text{i}\pi/6} =\sqrt{3}\text{e}^{-5\text{i}\pi/6} $
Par conséquent $z_2 = \overline{z_1} = \sqrt{3}\text{e}^{5\text{i}\pi/6}$
$$\begin{array}{rl} AB &= |z_2 – z_1| \\ &=\left|\text{i}\sqrt{3}\right| \\ &=\sqrt{3}
\end{array}$$
Par conséquent le triangle $OAB$ est équilatéral.
$$\begin{array}{rl} z’ &= (x+\text{i} y)^2 + 4(x + \text{i} y) + 3\\ &=x^2-y^2 + 2\text{i} xy + 4x + 4\text{i} y + 3\\ &= x^2 – y^2 + 4x + 3 + \text{i}(2xy + 4y) \\ & = x^2 – y^2 + 4x + 3 + 2y \text{i}(x + 2)
\end{array}$$
$z’$ est un nombre réel si, et seulement si, $2y(x+2) = 0$ ce qui est équivalent à $y = 0$ ou $x= – 2$.
L’ensemble $\mathscr{E}$ est donc la réunion de l’axe des abscisses et de la droite d’équation $x=-2$
Exercice 3 3 points
Dans un pays, la taille en centimètres des femmes de 18 à 65 ans peut être modélisée par une variable aléatoire $X_1$ suivant la loi normale d'espérance $\mu_1 = 165$ cm et d'écart-type$\sigma_1 = 6$ cm, et celle des hommes de 18 à 65 ans, par une variable aléatoire $X_2$ suivant la loi normale d'espérance $\mu_2 = 175$ cm et d'écart-type $\sigma_2 = 11$ cm.
Dans cet exercice tous les résultats seront arrondis à $10^{-2}$ près.
- Quelle est la probabilité qu'une femme choisie au hasard dans ce pays mesure entre 1,53 mètre et 1,77 mètre ?
-
- Déterminer la probabilité qu'un homme choisi au hasard dans ce pays mesure plus de 1,70 mètre.
- De plus, on sait que dans ce pays les femmes représentent 52 % de la population des personnes dont l'âge est compris entre 18 et 65 ans. On choisit au hasard une personne qui a entre 18 et 65 ans. Elle mesure plus de $1,70$ m. Quelle est la probabilité que cette personne soit une femme ?
Correction de l'exercice 3 (5 points)
Dans un pays, la taille en centimètres des femmes de 18 à 65 ans peut être modélisée par une variable aléatoire $X_1$ suivant la loi normale d'espérance $\mu_1 = 165$ cm et d'écart-type$\sigma_1 = 6$ cm, et celle des hommes de 18 à 65 ans, par une variable aléatoire $X_2$ suivant la loi normale d'espérance $\mu_2 = 175$ cm et d'écart-type $\sigma_2 = 11$ cm.
Dans cet exercice tous les résultats seront arrondis à $10^{-2}$ près.
- Quelle est la probabilité qu'une femme choisie au hasard dans ce pays mesure entre 1,53 mètre et 1,77 mètre ? On veut donc ici calculer $P(153\leq X_1\leq 177)$
-
- Déterminer la probabilité qu'un homme choisi au hasard dans ce pays mesure plus de 1,70 mètre. On calcule ici $P(X_2\geq 170)$
- De plus, on sait que dans ce pays les femmes représentent 52 % de la population des personnes dont l'âge est compris entre 18 et 65 ans. On choisit au hasard une personne qui a entre 18 et 65 ans. Elle mesure plus de $1,70$ m. Quelle est la probabilité que cette personne soit une femme ? Calculons $P(X_1 \ge 170) = 0,5 – P(165 \le X_1 \le 170) \approx 0,20$
2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
On appelle $G$ l’événement « la personne choisie mesure plus de $1,70$m ».
On appelle $F$ l’événement « la personne choisie est une femme ».
On peut alors représenter la situation par un arbre pondéré :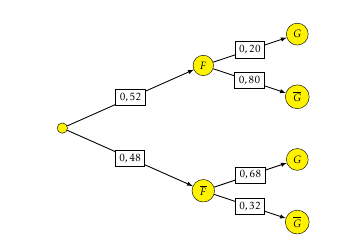
D’après la formule des probabilités totales on a :
$$\begin{array}{rl} p(G) &= p(F \cap G) + p\left(\overline{F} \cap G\right) \\ &= 0,52 \times 0,20 + 0,48 \times 0,68 \\ & \approx 0,43
\end{array}$$
$\quad$
Par conséquent :
$$\begin{array}{rl} p_G(F) &= \dfrac{p(G \cap F)}{p(G)} \\ &=\dfrac{0,52 \times 0,20}{0,43} \\ & \approx 0,24
\end{array}$$.
La probabilité que la personne choisie soit une femme sachant qu’elle mesure plus de $1,70$ m est donc de $0,24$.
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Remarque : $153= \mu_1-2\sigma_1$ et $177= \mu_1+ 2\sigma_1$; ainsi un résulat du cours donne $P(\mu_1-2\sigma_1\leq X_1\leq \mu_1+2\sigma_1) \approx 0,9545$
Exercice 4 5 points
Le directeur d'un zoo souhaite faire construire un toboggan pour les pandas. Il réalise le schéma suivant de ce toboggan en perspective cavalière. Voici ce schéma : 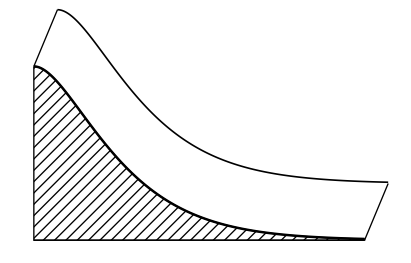
Partie A Modélisation
Le profil de ce toboggan est modélisé par la courbe $\mathcal{C}$ représentant la fonction $f$ définie sur l'intervalle [1 ; 8] par \[f(x) = (ax + b)\text{e}^{- x}\quad \text{où }\: a\:\: \text{et }\: b\: \text{sont deux entiers naturels.}\] La courbe $\mathcal{C}$ est tracée ci-dessous dans un repère orthonormé dont l'unité est le mètre. 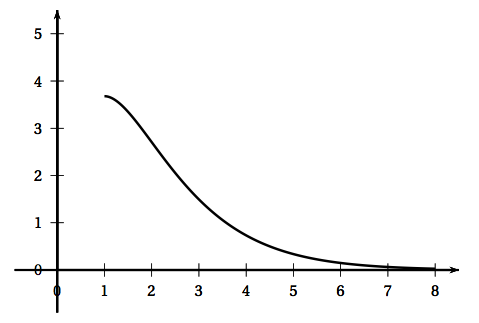
- On souhaite que la tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1 soit horizontale. Déterminer la valeur de l'entier $b$.
- On souhaite que le haut du toboggan soit situé entre $3,5$ et $4$ mètres de haut. Déterminer la valeur de l'entier $a$.
Partie B Un aménagement pour les visiteurs
On admet dans la suite que la fonction $f$ introduite dans la partie A est définie pour tout réel $x \in [1~;~8]$ par \[f(x) = 10x \text{e}^{- x}.\] Le mur de soutènement du toboggan sera peint par un artiste sur une seule face, hachurée sur le schéma en début d'exercice. Sur le devis qu'il propose, celui-ci demande un forfait de 300 euros augmenté de 50 euros par mètre carré peint.
- Soit $g$ la fonction définie sur [1 ; 8] par \[g(x) = 10(- x - 1)\text{e}^{-x}.\] Déterminer la fonction dérivée de la fonction $g$.
- Quel est le montant du devis de l'artiste ?
Partie C Une contrainte à vérifier
Des raisons de sécurité imposent de limiter la pente maximale du toboggan. On considère un point $M$ de la courbe $\mathcal{C}$, d'abscisse différente de 1. On appelle $\alpha$ l'angle aigu formé par la tangente en $M$ à $\mathcal{C}$ et l'axe des abscisses. La figure suivante illustre la situation. 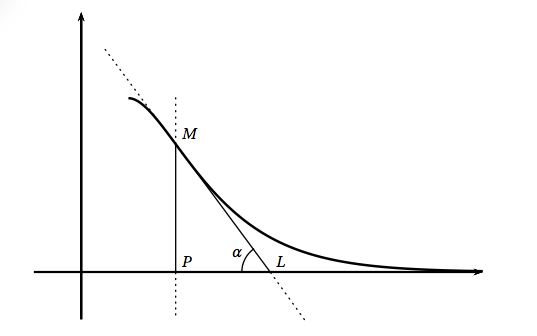
Les contraintes imposent que l'angle $\alpha$ soit inférieur à 55 degrés.
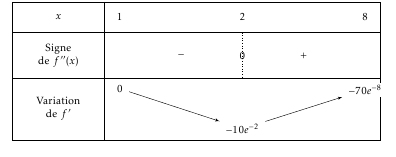
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [1 ; 8]. On admet que, pour tout $x$ de l'intervalle [1 ; 8], $f'(x) = 10(1- x)\text{e}^{-x}$. Étudier les variations de la fonction $f'$ sur l'intervalle [1 ; 8].
- Soit $x$ un réel de l'intervalle ]1 ; 8] et soit $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}$. Justifier que $\tan \alpha = \left|f'(x)\right|$.
- Le toboggan est-il conforme aux contraintes imposées ?
Exercice 4 5 points
Le directeur d'un zoo souhaite faire construire un toboggan pour les pandas. Il réalise le schéma suivant de ce toboggan en perspective cavalière. Voici ce schéma : 
Partie A Modélisation
Le profil de ce toboggan est modélisé par la courbe $\mathcal{C}$ représentant la fonction $f$ définie sur l'intervalle [1 ; 8] par \[f(x) = (ax + b)\text{e}^{- x}\quad \text{où }\: a\:\: \text{et }\: b\: \text{sont deux entiers naturels.}\] La courbe $\mathcal{C}$ est tracée ci-dessous dans un repère orthonormé dont l'unité est le mètre. 
- On souhaite que la tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1 soit horizontale. Déterminer la valeur de l'entier $b$. La fonction $f$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
- On souhaite que le haut du toboggan soit situé entre $3,5$ et $4$ mètres de haut. Déterminer la valeur de l'entier $a$. On a ainsi $f(x) = ax\text{e}^{-x}$.
$$\begin{array}{rl} f'(x) &= a\text{e}^{-x} -(ax+b)\text{e}^{-x} \\ &=(-ax + a – b)\text{e}^{-x} \end{array}$$
On veut la tangente à la courbe $\mathcal{C}$ au point d’abscisse $1$ soit horizontale. Cela signifie donc que :
$f'(1) = 0 \iff -a + a – b = 0 \iff b = 0$
On veut que trouver la valeur de l’entier naturel $a$ telle que :
$$\begin{array}{rl} 3,5 \le f(1) \le 4 &\iff 3,5 \le a\text{e}^{-1} \le 4 \\ & \iff 3,5\text{e} \le a \le 4\text{e} \\ & \iff 9,5\le 3,5\text{e} \le a \le 4\text{e} \le 10,9 \\ & \iff a = 10 \end{array}$$
Partie B Un aménagement pour les visiteurs
On admet dans la suite que la fonction $f$ introduite dans la partie A est définie pour tout réel $x \in [1~;~8]$ par \[f(x) = 10x \text{e}^{- x}.\] Le mur de soutènement du toboggan sera peint par un artiste sur une seule face, hachurée sur le schéma en début d'exercice. Sur le devis qu'il propose, celui-ci demande un forfait de 300 euros augmenté de 50 euros par mètre carré peint.
- Soit $g$ la fonction définie sur [1 ; 8] par \[g(x) = 10(- x - 1)\text{e}^{-x}.\] Déterminer la fonction dérivée de la fonction $g$. La fonction $g$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
- Quel est le montant du devis de l'artiste ? On a prouvé $g'(x)=f(x)$.
$$\begin{array}{rl} g'(x) &= 10 \left(-x\text{e}^{-x} – \left(-x – 1\right)\text{e}^{-1}\right) \\ &=10 (-x +x +1)\text{e}^{-x} \\ & = f(x) \end{array}$$
Ainsi $g$ est une primitive de $f$ sur $[1;8]$.
L’aire du mur à peindre correspond à l’aire du domaine compris entre l’axe des abscisses, la courbe $\mathcal{C}$ et les droites d’équation $x=1$ et $x=8$.
Il s’agit donc de :
$$\begin{array}{rl} \displaystyle I&= \int_1^8 f(x)\mathrm{d}x \\ &= \left[g(x)\right]_1^8 \\ & = g(8) – g(1) \\ &= -90\text{e}^{-8} + 20\text{e}^{-1} \end{array}$$ Le devis sera donc de $300 + 50 \times \left(-90\text{e}^{-8} + 20\text{e}^{-1} \right) \approx 666,37$ euros
Partie C Une contrainte à vérifier
Des raisons de sécurité imposent de limiter la pente maximale du toboggan. On considère un point $M$ de la courbe $\mathcal{C}$, d'abscisse différente de 1. On appelle $\alpha$ l'angle aigu formé par la tangente en $M$ à $\mathcal{C}$ et l'axe des abscisses. La figure suivante illustre la situation. 
Les contraintes imposent que l'angle $\alpha$ soit inférieur à 55 degrés.
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [1 ; 8]. On admet que, pour tout $x$ de l'intervalle [1 ; 8], $f'(x) = 10(1- x)\text{e}^{-x}$. Étudier les variations de la fonction $f'$ sur l'intervalle [1 ; 8]. La fonction $f’$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
- Soit $x$ un réel de l'intervalle ]1 ; 8] et soit $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}$. Justifier que $\tan \alpha = \left|f'(x)\right|$. Une équation de la tangente à la courbe $\mathcal{C}$ au point $M$ d’abscisse $a$ est donc de la forme $y=f'(a)(x-a) + f(a)$.
- Le toboggan est-il conforme aux contraintes imposées ? $\tan 55 \approx 1,43$.
$$\begin{array}{rl} f '' (x) &= 10\left(-\text{e}^{-x} – (1-x)\text{e}^{-x}\right) \\ &= 10(-1 -1 + x)\text{e}^{-x} \\ &=-10(-2+x)\text{e}^{-x}
\end{array}$$
La fonction exponentielle étant strictement positive, le signe de $f ''$ ne dépend que de celui de $-2+x$.
Ainsi la fonction $f’$ est décroissante sur $[1;2]$ et croissante sur $[2;8]$.
Le point $L$ est le point de cette droite tel que $y=0$.
Par conséquent
$$\begin{array}{rl} f'(a)(x_L-a) + f(a) = 0 &\iff f'(a)(x_L – a) = -f(a) \\ &\iff x_L – a = -\dfrac{f(a)}{f'(a)}
\end{array}$$.
Dans le triangle $MPL$ rectangle en $P$ on a :
$$\begin{array}{rl} \tan \alpha &= \dfrac{MP}{PL} \\ &=\dfrac{f(a)}{\left|x_L -a\right|} \\ & = \dfrac{f(a)}{\left|\dfrac{f(a)}{f'(a)}\right|} \\ &=\left|f'(a)\right| \end{array}$$
Ainsi pour tout point $M$ d’abscisse $x$ on a $\tan \alpha = \left|f'(x)\right|$.
La fonction $f’$ est négative sur $[1;8]$. Ainsi le maximum de $\left|f'(x)\right|$ est atteint pour $x=2$ (où $f’$ atteint son minimum).
or $|f'(2)| \approx 1,35 \le \tan 55$.
Par conséquent le toboggan est conforme.
Exercice 5 5 points
Soit $\left(v_n\right)$ la suite définie par \[v_1 = \ln (2) \quad \text{et, pour tout entier naturel }\: n \:\text{non nul},\: v_{n+1} = \ln \left(2 - \text{e}^{- v_n}\right).\] On admet que cette suite est définie pour tout entier naturel $n$ non nul. On définit ensuite la suite $\left(S_n\right)$ pour tout entier naturel $n$ non nul par : \[S_n = \displaystyle\sum_{k=1}^n v_k = v_1 + v_2 + \cdots + v_n.\] Le but de cet exercice est de déterminer la limite de $\left(S_n\right)$.
Partie A -- Conjectures à l'aide d'un algorithme
- Recopier et compléter l'algorithme suivant qui calcule et affiche la valeur de $S_n$ pour une valeur de $n$ choisie par l'utilisateur : $$ \begin{array}{|ll|}\hline \text{ Variables :} & n, k \text{ entiers }\\ &S, \:v \text{ réels}\\ \text{ Initialisation :}& \text{ Saisir la valeur de } n\\ &v \text{ prend la valeur } \ldots\\ &S \text{ prend la valeur } \ldots\\ \text{ Traitement :}& \text{ Pour } k \text{ variant de } \ldots \text{ à } \ldots \text{ faire }\\ &\hspace{0.4cm}\begin{array}{|l} \ldots \text{ prend la valeur }\ldots\\ \ldots \text{ prend la valeur } \ldots \end{array}\\ &\text{ Fin Pour}\\ Sortie :& \text{ Afficher} S\\ \hline \end{array} $$
- À l'aide de cet algorithme, on obtient quelques valeurs de $S_n$. Les valeurs arrondies au dixième sont données dans le tableau ci-dessous : $$ \begin{array}{|l|l|l|l|l|l|l| }\hline n &10 &100 & 1000 & 10000 & 100000 & 1000000 \\ \hline S_n &2,4&4,6 &6,9 &9,2 &11,5 &13,8\\ \hline \end{array} $$ En expliquant votre démarche, émettre une conjecture quant au comportement de la suite $\left(S_n\right)$.
Partie B -- Étude d'une suite auxiliaire
Pour tout entier naturel $n$ non nul, on définit la suite $\left(u_n\right)$ par $u_n = \text{e}^{v_n}$.
- Vérifier que $u_1 = 2$ et que, pour tout entier naturel $n$ non nul, $u_{n+1} = 2 - \dfrac{1}{u_n}$.
- Calculer $u_2,\: u_3$ et $u_4$. Les résultats seront donnés sous forme fractionnaire.
- Démontrer que, pour tout entier naturel $n$ non nul, $u_n = \dfrac{n+1}{n}$.
Partie C -- Étude de $(Sn)$
- Pour tout entier naturel $n$ non nul, exprimer $v_n$ en fonction de $u_n$, puis $v_n$ en fonction de $n$.
- Vérifier que $S_3 = \ln (4)$.
- Pour tout entier naturel $n$ non nul, exprimer $S_n$ en fonction de $n$. En déduire la limite de la suite $\left(S_n\right)$.
Correction de l'exercice 5 5 points
Soit $\left(v_n\right)$ la suite définie par \[v_1 = \ln (2) \quad \text{et, pour tout entier naturel }\: n \:\text{non nul},\: v_{n+1} = \ln \left(2 - \text{e}^{- v_n}\right).\] On admet que cette suite est définie pour tout entier naturel $n$ non nul. On définit ensuite la suite $\left(S_n\right)$ pour tout entier naturel $n$ non nul par : \[S_n = \displaystyle\sum_{k=1}^n v_k = v_1 + v_2 + \cdots + v_n.\] Le but de cet exercice est de déterminer la limite de $\left(S_n\right)$.
Partie A -- Conjectures à l'aide d'un algorithme
- Recopier et compléter l'algorithme suivant qui calcule et affiche la valeur de $S_n$ pour une valeur de $n$ choisie par l'utilisateur : $$ \begin{array}{|ll|}\hline \text{ Variables :} & n, k \text{ entiers }\\ &S, \:v \text{ réels}\\ \text{ Initialisation :}& \text{ Saisir la valeur de } n\\ &v \text{ prend la valeur } \ldots\\ &S \text{ prend la valeur } \ldots\\ \text{ Traitement :}& \text{ Pour } k \text{ variant de } \ldots \text{ à } \ldots \text{ faire }\\ &\hspace{0.4cm}\begin{array}{|l} \ldots \text{ prend la valeur }\ldots\\ \ldots \text{ prend la valeur } \ldots \end{array}\\ &\text{ Fin Pour}\\ Sortie :& \text{ Afficher} S\\ \hline \end{array} $$ Variables :
- À l'aide de cet algorithme, on obtient quelques valeurs de $S_n$. Les valeurs arrondies au dixième sont données dans le tableau ci-dessous : $$ \begin{array}{|l|l|l|l|l|l|l| }\hline n &10 &100 & 1000 & 10000 & 100000 & 1000000 \\ \hline S_n &2,4&4,6 &6,9 &9,2 &11,5 &13,8\\ \hline \end{array} $$ En expliquant votre démarche, émettre une conjecture quant au comportement de la suite $\left(S_n\right)$. Les valeurs de $S_n$ étant de plus en plus grande, on peut conjecturer que la suite $(S_n)$ est croissante et probablement de limite $+\infty$.
$\quad$ $n, k$ entiers
$\quad$ $S,v$ réels
Initialisation :
$\quad$ Saisir la valeur de $n$
$\quad$ $v$ prend la valeur $\ln(2)$
$\quad$ $S$ prend la $v$
Traitement :
$\quad$ Pour $k$ variant de $2$ à $n$ faire
$\qquad$ $v$ prend la valeur $\ln\left(2 – \text{e}^{-v}\right)$
$\qquad$ $S$ prend la valeur $S + v$
$\quad$ Fin Pour
Sortie :
$\quad$ Afficher $S$
Partie B -- Étude d'une suite auxiliaire
Pour tout entier naturel $n$ non nul, on définit la suite $\left(u_n\right)$ par $u_n = \text{e}^{v_n}$.
- Vérifier que $u_1 = 2$ et que, pour tout entier naturel $n$ non nul, $u_{n+1} = 2 - \dfrac{1}{u_n}$. $u_1 = \text{e}^{\ln(2)} = 2$.
- Calculer $u_2,\: u_3$ et $u_4$. Les résultats seront donnés sous forme fractionnaire. On a ainsi $u_2 = 2 – \dfrac{1}{2} = \dfrac{3}{2}$
- Démontrer que, pour tout entier naturel $n$ non nul, $u_n = \dfrac{n+1}{n}$. Montrons cette propriété par récurrence.
$$\begin{array}{rl} u{n+1} &= \text{e}^{v_{n+1}} \\ &= 2 – e^{-v_n} \\ &= 2 – \dfrac{1}{e^{v_n}} \\ &=2 – \dfrac{1}{u_n} \end{array}$$
$\quad$
$u_3 = 2 – \dfrac{2}{3} = \dfrac{4}{3}$
Initialisation :
Pour $n=1$, $\dfrac{n+1}{n} = 2 = u_1$.
La propriété est donc vraie au rang $1$.
$\quad$
Hérédité :
Supposons la propriété vraie au rang $n$ : $u_n = \dfrac{n+1}{n}$
Alors $$\begin{array}{rl} u_{n+1} &= 2 – \dfrac{1}{u_n} \\ & = 2 – \dfrac{n}{n+1} \\ & = \dfrac{2n + 2 -n}{n+1} \\ &= \dfrac{n+2}{n+1} \end{array}$$
La propriété est donc vraie au rang $n+1$
Conclusion :
La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a $u_n = \dfrac{n+1}{n}$.
Partie C -- Étude de $(Sn)$
- Pour tout entier naturel $n$ non nul, exprimer $v_n$ en fonction de $u_n$, puis $v_n$ en fonction de $n$. On a $u_n = \dfrac{n+1}{n}$.
- Vérifier que $S_3 = \ln (4)$. $$\begin{array}{rl} S_3 &= v_1 + v_2 + v_3 \\ &= \ln(2) + \ln(3) – \ln(2) + \ln(4) – \ln(3) \\ & = \ln(4) \end{array}$$
- Pour tout entier naturel $n$ non nul, exprimer $S_n$ en fonction de $n$. En déduire la limite de la suite $\left(S_n\right)$. On a :
Or $$\begin{array}{rl} u_n = \text{e}^{v_n} &\iff v_n = \ln u_n \\ & \iff v_n = \ln \dfrac{n+1}{n} \\ & \iff v_n = \ln (n+1) – \ln (n) \end{array}$$
$$\displaystyle \begin{array}{rl} S_n &= \displaystyle\sum_{k=1}^n v_k \\ &= \ln(2) + \ln(3) – \ln(2) + \ldots + \ln(n-1) – \ln(n-2) + \ln(n) – \ln(n-1) \\ & = \ln(n) \end{array}$$
Or $\lim\limits_{x \to +\infty} \ln(x) = +\infty$ donc $\lim\limits_{n \to +\infty} S_n= +\infty$.
Spécialité 5 points
On considère la matrice $A = \begin{pmatrix}-4&6\\- 3& 5\end{pmatrix}$
- On appelle $I$ la matrice identité d'ordre 2. Vérifier que $A^2 = A + 2I$.
- En déduire une expression de $A^3$ et une expression de $A^4$ sous la forme $\alpha A + \beta I$ où $\alpha$ et $\beta$ sont des réels.
- On considère les suites $\left(r_n\right)$ et $\left(s_n\right)$ définies par $r_0 = 0$ et $s_0 = 1$ et, pour tout entier naturel $n$ non nul, \[\left\{\begin{array}{l c l} r_{n+1}&=&\phantom{2}r_n + s_n\\ s_{n+1}&=&2r_n \end{array}\right.\] Démontrer que, pour tout entier naturel $n,\: A^n = r_nA + s_nI$.
- Démontrer que la suite $\left(k_n\right)$ définie pour tout entier naturel $n$ non nul par $k_n = r_n - s_n$ est géométrique de raison $- 1$. En déduire, pour tout entier naturel $n$ non nul, une expression explicite de $k_n$ en fonction de $n$.
- On admet que la suite $\left(t_n\right)$ définie pour tout entier naturel $n$ non nul par $t_n = r_n + \dfrac{(- 1)^n}{3}$ est géométrique de raison 2. En déduire, pour tout entier naturel $n$ non nul, une expression explicite de $t_n$ en fonction de $n$.
- Déduire des questions précédentes, pour tout entier naturel $n$ non nul, une expression explicite de $r_n$ et $s_n$ en fonction de $n$.
- En déduire alors, pour tout entier naturel $n$ non nul, une expression des coefficients de la matrice $A^n$.
Correction de l'exercice de Spécialité 5 points
On considère la matrice $A = \begin{pmatrix}-4&6\\- 3& 5\end{pmatrix}$
- On appelle $I$ la matrice identité d'ordre 2. Vérifier que $A^2 = A + 2I$. $A^2 = \begin{pmatrix} -2&6 \\-3&7 \end{pmatrix}$
- En déduire une expression de $A^3$ et une expression de $A^4$ sous la forme $\alpha A + \beta I$ où $\alpha$ et $\beta$ sont des réels. On a ainsi
- On considère les suites $\left(r_n\right)$ et $\left(s_n\right)$ définies par $r_0 = 0$ et $s_0 = 1$ et, pour tout entier naturel $n$ non nul, \[\left\{\begin{array}{l c l} r_{n+1}&=&\phantom{2}r_n + s_n\\ s_{n+1}&=&2r_n \end{array}\right.\] Démontrer que, pour tout entier naturel $n,\: A^n = r_nA + s_nI$. Montrons cette propriété par récurrence.
- Démontrer que la suite $\left(k_n\right)$ définie pour tout entier naturel $n$ non nul par $k_n = r_n - s_n$ est géométrique de raison $- 1$. En déduire, pour tout entier naturel $n$ non nul, une expression explicite de $k_n$ en fonction de $n$. $$\begin{array}{rl} k_{n+1} &= r_{n+1} – s_{n+1} \\ &= r_n + s_n – 2r_n \\ & = s_n – r_n \\ & = -k_n \end{array}$$
- On admet que la suite $\left(t_n\right)$ définie pour tout entier naturel $n$ non nul par $t_n = r_n + \dfrac{(- 1)^n}{3}$ est géométrique de raison 2. En déduire, pour tout entier naturel $n$ non nul, une expression explicite de $t_n$ en fonction de $n$. On a $t_1 = 1 + \dfrac{-1}{3} = \dfrac{2}{3}$
- Déduire des questions précédentes, pour tout entier naturel $n$ non nul, une expression explicite de $r_n$ et $s_n$ en fonction de $n$. On a donc $r_n = t_n – \dfrac{(-1)^n}{3} = \dfrac{2}{3} \times 2^{n-1} – \dfrac{(-1)^n}{3}$
- En déduire alors, pour tout entier naturel $n$ non nul, une expression des coefficients de la matrice $A^n$. $$\begin{array}{rl} A ^n &=r_n A + s_n I\\ & = r_n \begin{pmatrix}-4&6\\- 3& 5\end{pmatrix} + s_n \begin{pmatrix}1&0\\0& 1\end{pmatrix}\\ & = \begin{pmatrix}-4r_n+s_n&6r_n\\ 3r_n& 5r_n + s_n\end{pmatrix} \\ \end{array}$$ $-4r_n + s_n = -2\times 2^{n-1} + (-1)^n + (-1)^n = -2^n + 2(-1)^n$
Or $A + 2I = \begin{pmatrix} -4 + 2&6 \\-3 &5 +2 \end{pmatrix} = A^2$
$$\begin{array}{rl} A^3 &= A \times A^2 \\ &= A \left(A + 2I\right) \\ & = A^2 + 2A \\ & = A + 2I + 2A \\ & = 3A + 2I \end{array}$$
$\quad$
De même
$$\begin{array}{rl} A^4 & = A \times A^3 \\ & = 3A^2 + 2A \\ &= 3A + 6I + 2A \\ &= 5A + 6I \end{array}$$
Initialisation :
Pour $n = 0$, $A^0 = I = 0A + 1I = r_0A + s_0I$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité :
Supposons la propriété vraie au rang $n$ : $A^n = r_nA + s_nI$.
Ainsi :
$$\begin{array}{rl} A^{n+1} &= A \times A^{n} \\ &= A\left(r_n A + s_n I\right) \\ & = r_n A^2 + s_n A \\ & = r_nA + 2r_n I + s_n A \\ & = \left(r_n + s_n\right)A + 2r_n I \\ &= r_{n+1}A + s_{n+1}I
\end{array}$$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion
La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $A^n = r_n A + s_n I$.
La suite $(k_n)$ est donc géométrique de raison $-1$ et de premier terme $k_0 = 0 – 1 = -1$.
$\quad$
Par conséquent $k_n = q^n k_0= -(-1)^n = (-1)^{n+1}$ pour tout entier naturel $n$.
Par conséquent $t_n =q^{n-1}\times t_1= \dfrac{2}{3} \times 2^{n-1}$.
$\quad$
$$r_n = \dfrac{2^n -(-1)^n}{3}$$De plus
$$\begin{array}{rl} s_n &= r_n – k_n \\ & = \dfrac{2}{3} \times 2^{n-1} – \dfrac{(-1)^n}{3} – (-1)^{n+1} \\ &= \dfrac{2}{3} \times 2^{n-1} + \dfrac{(-1)^{n+1}}{3} + (-1)^n \\ &= \dfrac{2^n}{3} - \dfrac{(-1)^{n }}{3} +\dfrac{3(-1)^{n }}{3} \\ &= \dfrac{2^n + 2 (-1)^{n } }{3} \end{array}$$
$5r_n + s_n = 4 \times 2^{n-1} – 2\times(-1)^n + (-1)^n = 2^{n+1} – (-1)^n$
$6r_n = 4\times 2^{n-1} – 2(-1)^n = 2^{n+1} – 2(-1)^n$
$-3r_n = -2\times 2^{n-1} + (-1)^n = -2^n + (-1)^n$
Donc $$A^n = \begin{pmatrix} -2^n + 2(-1)^n & 2^{n+1} – 2(-1)^n \\ -2^n + (-1)^n & 2^{n+1} – (-1)^n \end{pmatrix}$$
- Vues: 31324
