Baccalauréat S Pondichéry 22 avril 2016
Exercice 1 4 points
Les deux parties A et B peuvent être traitées de façon indépendante
Partie A
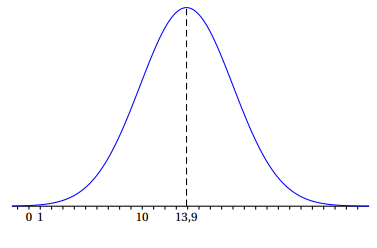
Des études statistiques ont permis de modéliser le temps hebdomadaire, en heures, de connexion à internet des jeunes en France âgés de 16 à 24 ans par une variable aléatoire $T$ suivant une loi normale de moyenne $\mu = 13,9$ et d'écart type $\sigma$. La fonction densité de probabilité de $T$ est représentée ci-dessous :
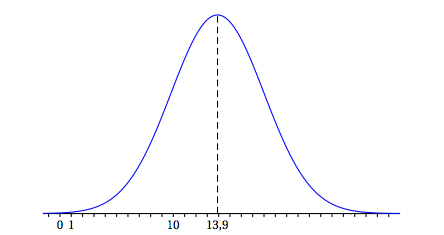
- On sait que $p(T \geqslant 22) = 0,023$. En exploitant cette information :
- hachurer sur le graphique donné un annexe, deux domaines distincts dont l'aire est égale à $0,023$ ;
- déterminer $P(5,8 \leqslant T \leqslant 22)$. Justifier le résultat. Montrer qu'une valeur approchée de $\sigma$ au dixième est $4,1$.
- On choisit un jeune en France au hasard. Déterminer la probabilité qu'il soit connecté à internet plus de 18 heures par semaine. Arrondir au centième.
Partie B
Dans cette partie, les valeurs seront arrondies au millième. La Hadopi (Haute Autorité pour la diffusion des Œuvres et la Protection des droits sur Internet) souhaite connaître la proportion en France de jeunes âgés de 16 à 24 ans pratiquant au moins une fois par semaine le téléchargement illégal sur internet. Pour cela, elle envisage de réaliser un sondage. Mais la Hadopi craint que les jeunes interrogés ne répondent pas tous de façon sincère. Aussi, elle propose le protocole $(\mathcal{P})$ suivant :
On choisit aléatoirement un échantillon de jeunes âgés de 16 à 24 ans. Pour chaque jeune de cet échantillon :
Grâce à ce protocole, l'enquêteur ne sait jamais si la réponse donnée porte sur la question posée ou résulte du lancer de dé, ce qui encourage les réponses sincères.
On note $p$ la proportion inconnue de jeunes âgés de 16 à 24 ans qui pratiquent au moins une fois par semaine le téléchargement illégal sur internet.
- Calculs de probabilités
On choisit aléatoirement un jeune faisant parti du protocole $(\mathcal{P})$. On note : $R$ l'évènement « le résultat du lancer est pair», $O$ l'évènement « le jeune a répondu Oui ».
Reproduire et compléter l'arbre pondéré ci-dessous :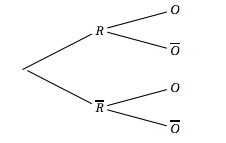
En déduire que la probabilité $q$ de l'évènement « le jeune a répondu Oui» est : \[q = \dfrac{1}{2}p + \dfrac{1}{6}.\] - Intervalle de confiance
- À la demande de l'Hadopi, un institut de sondage réalise une enquête selon le protocole $(\mathcal{P})$. Sur un échantillon de taille 1500} , il dénombre $625$ réponses « Oui ». Donner un intervalle de confiance, au niveau de confiance de 95%, de la proportion $q$ de jeunes qui répondent « Oui » à un tel sondage, parmi la population des jeunes français âgés de 16 à 24 ans.
- Que peut-on en conclure sur la proportion $p$ de jeunes qui pratiquent au moins une fois par semaine le téléchargement illégal sur internet ?
Correction de l'exercice 1 ( 4 points)
Les deux parties A et B peuvent être traitées de façon indépendante
Partie A
Des études statistiques ont permis de modéliser le temps hebdomadaire, en heures, de connexion à internet des jeunes en France âgés de 16 à 24 ans par une variable aléatoire $T$ suivant une loi normale de moyenne $\mu = 13,9$ et d'écart type $\sigma$. La fonction densité de probabilité de $T$ est représentée ci-dessous :

- On sait que $p(T \geqslant 22) = 0,023$. En exploitant cette information :
- hachurer sur le graphique donné un annexe, deux domaines distincts dont l'aire est égale à $0,023$ ; $22-13,9=8,1$ et $13,9-8,1=5,8$
- déterminer $P(5,8 \leqslant T \leqslant 22)$. Justifier le résultat. Montrer qu'une valeur approchée de $\sigma$ au dixième est $4,1$.
Par symétrie, on a donc $P(X \leqslant 5,8)=P(X \geqslant 22)$.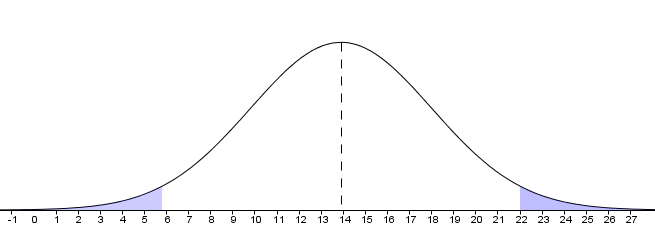
$\quad$
$\begin{align*} P(5,8 \leqslant T \leqslant 22) &= 1-\left(P(T\leqslant 5,8)+P(T\geqslant 22)\right) \\ - On choisit un jeune en France au hasard. Déterminer la probabilité qu'il soit connecté à internet plus de 18 heures par semaine. Arrondir au centième. On veut calculer $P(T \geqslant 18)=0,5-P(13,9 \leqslant T \leqslant 18) \approx 0,16$.
&=1-2\times 0,023 \\
&=0,954
\end{align*}$
$\quad$
Or $P(\mu-2\sigma \leqslant X \leqslant \mu+2\sigma) \approx 0,954$
Donc $13,9-2\sigma \approx 5,8$ soit $\sigma \approx 4,05$ et $\sigma \approx 4,1$ arrondi au dixième.
$\quad$
$\quad$ En vidéo !
Partie B
Dans cette partie, les valeurs seront arrondies au millième. La Hadopi (Haute Autorité pour la diffusion des Œuvres et la Protection des droits sur Internet) souhaite connaître la proportion en France de jeunes âgés de 16 à 24 ans pratiquant au moins une fois par semaine le téléchargement illégal sur internet. Pour cela, elle envisage de réaliser un sondage. Mais la Hadopi craint que les jeunes interrogés ne répondent pas tous de façon sincère. Aussi, elle propose le protocole $(\mathcal{P})$ suivant :
On choisit aléatoirement un échantillon de jeunes âgés de 16 à 24 ans. Pour chaque jeune de cet échantillon :
Grâce à ce protocole, l'enquêteur ne sait jamais si la réponse donnée porte sur la question posée ou résulte du lancer de dé, ce qui encourage les réponses sincères.
On note $p$ la proportion inconnue de jeunes âgés de 16 à 24 ans qui pratiquent au moins une fois par semaine le téléchargement illégal sur internet.
- Calculs de probabilités
On choisit aléatoirement un jeune faisant parti du protocole $(\mathcal{P})$. On note : $R$ l'évènement « le résultat du lancer est pair», $O$ l'évènement « le jeune a répondu Oui ».
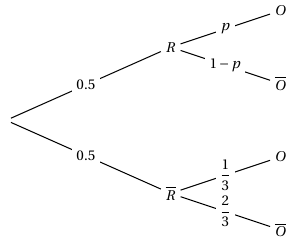
Reproduire et compléter l'arbre pondéré ci-dessous :
En déduire que la probabilité $q$ de l'évènement « le jeune a répondu Oui» est : \[q = \dfrac{1}{2}p + \dfrac{1}{6}.\] $\quad$ - Intervalle de confiance
- À la demande de l'Hadopi, un institut de sondage réalise une enquête selon le protocole $(\mathcal{P})$. Sur un échantillon de taille 1500} , il dénombre $625$ réponses « Oui ». Donner un intervalle de confiance, au niveau de confiance de 95%, de la proportion $q$ de jeunes qui répondent « Oui » à un tel sondage, parmi la population des jeunes français âgés de 16 à 24 ans. Un intervalle de confiance qu seuil de $95\%$ de la proportion $q$ est :
- Que peut-on en conclure sur la proportion $p$ de jeunes qui pratiquent au moins une fois par semaine le téléchargement illégal sur internet ? Par conséquent $0,390 \leqslant \dfrac{1}{2}p+\dfrac{1}{6} \leqslant 0,443 $
$\begin{align*} I_{1500}~&=\left[\dfrac{625}{1~500}-\dfrac{1}{\sqrt{1~500}};\dfrac{625}{1~500}+\dfrac{1}{\sqrt{1~500}}\right] \\
& \approx [0,390;0,443]
\end{align*}$
$\quad$
Soit $0,390-\dfrac{1}{6}\leqslant \dfrac{1}{2}p \leqslant 0,443 -\dfrac{1}{6}$
Et donc $2\times \left(0,390-\dfrac{1}{6}\right)\leqslant p \leqslant 2\times \left(0,443 -\dfrac{1}{6}\right)$
En arrondissant au millième, on trouve :
$0,446 \leqslant p \leqslant 0,553$
Par conséquent entre $44,6\%$ et $55,3\%$ des jeunes pratiquent au moins une fois par semaine le téléchargement illégal sur internet.
$\quad$
D’après la formule des probabilités totales, on a :
$\begin{align*} p(O)&=p(R\cap O)+p\left(\overline{R}\cap O\right) \\
&=\dfrac{1}{2}p+\dfrac{1}{2}\times \dfrac{1}{3} \\
&=\dfrac{1}{2}p+\dfrac{1}{6}
\end{align*}$
$\quad$
Exercice 2 3 points
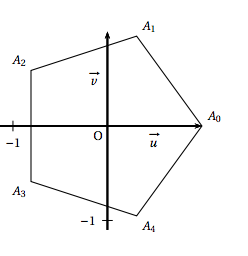
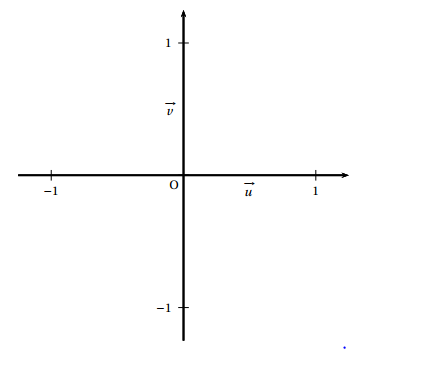
Dans le plan complexe muni d'un repère orthonormé direct $(O; \vec {u}, \vec{v})$, on considère le pentagone régulier $A_0A_1A_2A_3A_4$, de centre $O$ tel que $\vec{OA_0} = \vec{u}$. On rappelle que dans le pentagone régulier $A_0A_1A_2A_3A_4$, ci-contre :
- les cinq côtés sont de même longueur;
- les points $A_0,\:A_1,\:A_2,\:A_3$ et $A_4$ appartiennent au cercle trigonométrique ;
- pour tout entier $k$ appartenant à $\{0~;~1~;~2~;~3\}$ on a $\left(\vec{OA_k}~;~\vec{OA_{k+1}}\right) = \dfrac{2\pi}{5}$.
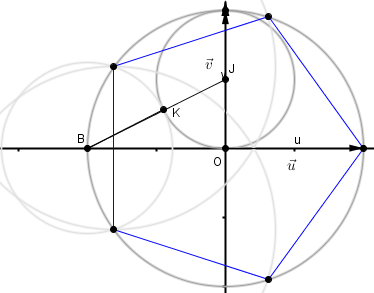
- On considère les points $B$ d'affixe $- 1$ et $J$ d'affixe $\dfrac{\text{i}}{2}$. Le cercle $(\mathcal{C})$ de centre $J$ et de rayon $\dfrac{1}{2}$ coupe le segment $[BJ]$ en un point $K$. Calculer $BJ$, puis en déduire $BK$.
- Donner sous forme exponentielle l'affixe du point $A_2$. Justifier brièvement.
- Démontrer que $BA_2\,^2 = 2 + 2\cos \left(\dfrac{4\pi}{5}\right)$.
- Un logiciel de calcul formel affiche les résultats ci-dessous, que l'on pourra utiliser sans justification : $$\begin{array}{|c|c|}\hline \blacktriangleright \text{ Calcul formel}\\\hline 1&cos (4*pi/5)\\ & \to \dfrac{1}{4}\left(- \sqrt{5} - 1\right) \\ \hline 2& sqrt((3 - sqrt(5))/2)\\ \hline & \to \dfrac{1}{2}\left(\sqrt{5} - 1\right) \\ \hline \end{array}$$ « sqrt » signifie « racine carrée» En déduire, grâce à ces résultats, que $BA_2 = BK$.
- Dans le repère $(O; \vec {u}, \vec{v})$ donné en annexe, construire à la règle et au compas un pentagone régulier.
N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.
Correction de l'exercice 2 (3 points)
Dans le plan complexe muni d'un repère orthonormé direct $(O; \vec {u}, \vec{v})$, on considère le pentagone régulier $A_0A_1A_2A_3A_4$, de centre $O$ tel que $\vec{OA_0} = \vec{u}$. On rappelle que dans le pentagone régulier $A_0A_1A_2A_3A_4$, ci-contre :
- les cinq côtés sont de même longueur;
- les points $A_0,\:A_1,\:A_2,\:A_3$ et $A_4$ appartiennent au cercle trigonométrique ;
- pour tout entier $k$ appartenant à $\{0~;~1~;~2~;~3\}$ on a $\left(\vec{OA_k}~;~\vec{OA_{k+1}}\right) = \dfrac{2\pi}{5}$.

- On considère les points $B$ d'affixe $- 1$ et $J$ d'affixe $\dfrac{\text{i}}{2}$. Le cercle $(\mathcal{C})$ de centre $J$ et de rayon $\dfrac{1}{2}$ coupe le segment $[BJ]$ en un point $K$. Calculer $BJ$, puis en déduire $BK$. $BJ=\left|\dfrac{\text{i}}{2}+1\right| = \sqrt{\dfrac{5}{4}}=\dfrac{\sqrt{5}}{2}$
- Donner sous forme exponentielle l'affixe du point $A_2$. Justifier brièvement. On appelle $z_2$ l’affixe de $A_2$. $A_2$ appartient au cercle trigonométrique donc $\left|z_2\right|=1$.
- Démontrer que $BA_2\,^2 = 2 + 2\cos \left(\dfrac{4\pi}{5}\right)$. $\begin{align*} BA_2 ^2 &= \left|z_2+1\right|^2 \\
$B, K$ et $J$ sont alignés dans cet ordre. Donc $BK=BJ-\dfrac{1}{2}=\dfrac{\sqrt{5}-1}{2}$.
$\quad$
$arg\left(z_2\right)=2\times \dfrac{2\pi}{5}=\dfrac{4\pi}{5}$.
Ainsi $z_2=\text{e}^{4\text{i}\pi/5}$.
$\quad$
&=\left|\cos\left(\dfrac{4\pi}{5}\right)+1+\text{i}\sin \left(\dfrac{4\pi}{5}\right)\right|^2 \\
&=\left(1+\cos\left(\dfrac{4\pi}{5}\right)\right)^2+\left(\sin\left(\dfrac{4\pi}{5}\right)\right)^2 \\
&=1+2\cos\left(\dfrac{4\pi}{5}\right)+\left(\cos\left(\dfrac{4\pi}{5}\right)\right)^2+\left(\sin\left(\dfrac{4\pi}{5}\right)\right)^2 \\
&=2+2\cos\left(\dfrac{4\pi}{5}\right)
\end{align*}$
$\quad$
$\begin{align*} BA_2 ^2 &= 2+2\times\dfrac{1}{4}\left(-\sqrt{5}-1\right) \\
&=\dfrac{4-\sqrt{5}-1}{2} \\
&=\dfrac{3-\sqrt{5}}{2}
\end{align*}$
Par conséquent $BA_2=\sqrt{\dfrac{3-\sqrt{5}}{2}}=\dfrac{\sqrt{5}-1}{2}=BK$
$\quad$
N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.
On place le point $B$ et le point $J$.
A l’aide des graduation fournie on trace le cercle de centre $J$ et de rayon $0.5$, ce qui permet de placer le point $K$.
On trace le cercle de centre $O$ et de rayon $1$ et on repporte à partir de $B$ la distance $BK$ sur ce cercle, ce qui permet de trouver les points $A_2$ et $A_3$.
On possède maintenant deux points consécutifs de ce pentagone régulier, ce qui permet de placer les autres points en reportant la distance les séparant sur le cercle trigonométrique.
$\quad$
Exercice 3 5 points
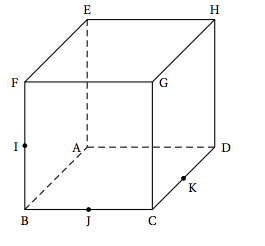
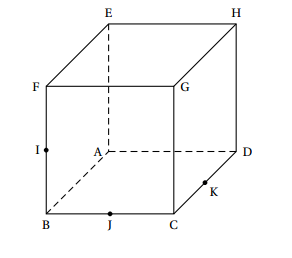
ABCDEFGH désigne un cube de côté 1. Le point I est le milieu du segment [BF]. Le point J est le milieu du segment [BC]. Le point K est le milieu du segment [CD].}
Partie A
Dans cette partie, on ne demande aucune justification
On admet que les droites (IJ) et (CG) sont sécantes en un point L. Construire, sur la figure fournie en annexe et en laissant apparents les traits de construction:
- le point L ;
- l'intersection $\mathcal{D}$ des plans (IJK) et (CDH) ;
- la section du cube par le plan (IJK).
Partie B
L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Donner les coordonnées de A, G, I, J et K dans ce repère.
-
- Montrer que le vecteur $\vec{\text{AG}}$ est normal au plan (IJK).
- En déduire une équation cartésienne du plan (IJK).
- On désigne par $M$ un point du segment [AG] et $t$ le réel de l'intervalle [0~;~1] tel que $\vec{\text{A}M} = t\vec{\text{AG}}$.
- Démontrer que $M\text{I}^2 = 3t^2 - 3t + \dfrac{5}{4}$.
- Démontrer que la distance $M$I est minimale pour le point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$.
- Démontrer que pour ce point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$ :
- $M$ appartient au plan (IJK).
- La droite (I$M$) est perpendiculaire aux droites (AG) et (BF).
Correction de l'exercice 3 (5 points)
ABCDEFGH désigne un cube de côté 1. Le point I est le milieu du segment [BF]. Le point J est le milieu du segment [BC]. Le point K est le milieu du segment [CD].}

Partie A
Dans cette partie, on ne demande aucune justification
On admet que les droites (IJ) et (CG) sont sécantes en un point L. Construire, sur la figure fournie en annexe et en laissant apparents les traits de construction:
- le point L ;
- l'intersection $\mathcal{D}$ des plans (IJK) et (CDH) ;
- la section du cube par le plan (IJK).
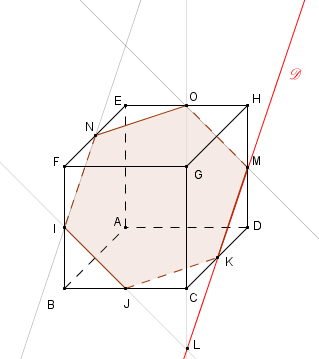
Les droites $(IJ)$ et $(OM)$ sont parallèles. C’est également le cas des droites $(KM)$ et $(NI)$ d’une part et $(NO)$ et $(JK)$ d’autre part.
$\quad$
Partie B
L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Donner les coordonnées de A, G, I, J et K dans ce repère. Dans le repère $\left(O;\vec{AB},\vec{AD},\vec{AE}\right)$ on a :
-
- Montrer que le vecteur $\vec{\text{AG}}$ est normal au plan (IJK). $\vec{AG}(1;1;1)$
- En déduire une équation cartésienne du plan (IJK). Par conséquent une équation du plan $(IJK)$ est de la forme
$\vec{IJ}(0;0,5;-0,5)$ donc $\vec{IJ}.\vec{AG}=0+0,5-0,5=0$. Ces vecteurs sont donc orthogonaux.
$\vec{IK}(-0,5;1;-0,5)$ donc $\vec{IK}.\vec{AG}=-0,5+1-0,5=0$. Ces vecteurs sont donc également orthogonaux.
Ainsi $\vec{AG}$ est orthogonal à deux vecteurs non colinéaires (c’est évident qu’ils ne le sont pas ) du plan $(IJK)$.
Il est donc normal à ce plan.
$\quad$
$$x+y+z+d=0$$
Le point $I$ appartient à ce plan. Ces coordonnées vérifient donc son équation cartésienne.
Ainsi $1+0+0,5+d=0$ donc $d=-1,5$.
Une équation cartésienne de $(IJK)$ est donc $x+y+z-1,5=0$.
$\quad$ - On désigne par $M$ un point du segment [AG] et $t$ le réel de l'intervalle [0~;~1] tel que $\vec{\text{A}M} = t\vec{\text{AG}}$.
- Démontrer que $M\text{I}^2 = 3t^2 - 3t + \dfrac{5}{4}$. Puisque $\vec{AM}=t\vec{AG}$ cela signifie que $\vec{AM}(t;t;t)$.
- Démontrer que la distance $M$I est minimale pour le point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$. On appelle $f$ la fonction définie sur $[0;1]$ par $f(t)=3t^2-3t+\dfrac{5}{4}$.
Ainsi $M$ a pour coordonnées $(t;t;t)$.
$\begin{align*} MI^2&=(t-1)^2+t^2+(t-0,5)^2 \\
&=t^2-2t+1+t^2+t^2-t+0,25 \\
&=3t^2-3t+1,25\\
&=3t^2-3t+\dfrac{5}{4}
\end{align*}$
Puisque $a=3>0$, cette fonction du second degré admet un minimum pour $t=\dfrac{3}{6}=\dfrac{1}{2}$.
Par conséquent, le point de $[AG]$ associé à cette valeur est $N\left(\dfrac{1}{2};\dfrac{1}{2};\dfrac{1}{2}\right)$.
$\quad$
En vidéo ! - Démontrer que pour ce point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$ :
- $M$ appartient au plan (IJK). Regardons si les coordonnées du point $N$ vérifient l’équation cartésienne du plan $(IJK)$.
- La droite (I$M$) est perpendiculaire aux droites (AG) et (BF). $\vect{IN}\left(-\dfrac{1}{2};\dfrac{1}{2};0\right)$.
$\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}-1,5=0$.
Donc $N$ appartient bien à $(IJK)$.
$\quad$
On a $\vect{AG}(1;1;1)$ donc $\vect{IN}.\vect{AG}=-\dfrac{1}{2}+\dfrac{1}{2}+0=0$.
$\vect{BF}(0;0;1)$ donc $\vect{IN}.\vect{BF}=0+0+0=0$.
Ainsi $\vect{IN}$ est orthogonal à $\vect{AG}$ et $\vect{BF}$.
$N$ appartient à $(IN)$ et $(AG)$ donc ces deux droites sont perpendiculaires.
$I$ appartient à $(IN)$ et $(BF)$ donc ces deux droites sont également perpendiculaires.
$\quad$
$A(0;0;0)$, $G(1;1;1)$, $I(1;0;0,5)$, $J(1;0,5;0)$ et $K(0,5;1;0)$.
$\quad$
Exercice 4 3 points
Soit $f$ la fonction définie sur $]0~;~14]$ par \[f(x) = 2 - \ln\left(\dfrac{x}{2}\right).\] La courbe représentative $\mathcal{C}_f$ de la fonction $f$ est donnée dans le repère orthogonal d'origine O ci-dessous :
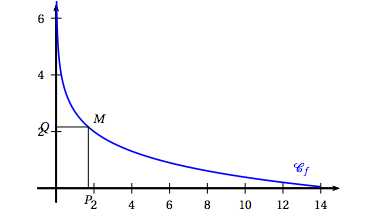
À tout point $M$ appartenant à $\mathcal{C}_f$ on associe le point $P$ projeté orthogonal de $M$ sur l'axe des abscisses, et le point $Q$ projeté orthogonal de $M$ sur l'axe des ordonnées.
- L'aire du rectangle O$PMQ$ est-elle constante quelle que soit la position du point $M$ sur $\mathcal{C}_f$ ?
- L'aire du rectangle O$PMQ$ peut-elle être maximale ? Si oui, préciser les coordonnées du point $M$ correspondant.
Justifier les réponses.
Correction de l'exercice 4 3 points
Soit $f$ la fonction définie sur $]0~;~14]$ par \[f(x) = 2 - \ln\left(\dfrac{x}{2}\right).\] La courbe représentative $\mathcal{C}_f$ de la fonction $f$ est donnée dans le repère orthogonal d'origine O ci-dessous :

À tout point $M$ appartenant à $\mathcal{C}_f$ on associe le point $P$ projeté orthogonal de $M$ sur l'axe des abscisses, et le point $Q$ projeté orthogonal de $M$ sur l'axe des ordonnées.
- L'aire du rectangle O$PMQ$ est-elle constante quelle que soit la position du point $M$ sur $\mathcal{C}_f$ ?
- L'aire du rectangle O$PMQ$ peut-elle être maximale ? Si oui, préciser les coordonnées du point $M$ correspondant.
Justifier les réponses.
On a $O(0;0)$, $P(x;0)$, $M(x;f(x))$ et $Q(0;f(x))$.
Donc l’aire du rectangle $OPMQ$ est $\mathscr{A}(x)=xf(x)=2x-x\ln \left(\dfrac{x}{2}\right)$.
Cette fonction $\mathscr{A}$ définie sur $]0;14]$ est dérivable sur cet intervalle en tant que somme et produits de fonctions dérivables sur cet intervalle.
$\mathscr{A}'(x)=2-\ln \left(\dfrac{x}{2}\right)-x\times \dfrac{1}{2}\times \dfrac{1}{\dfrac{x}{2}}=1-\ln \left(\dfrac{x}{2}\right)$.
Or :
$\begin{align*} 1-\ln \left(\dfrac{x}{2}\right) = 0 &\Leftrightarrow \ln \left(\dfrac{x}{2}\right) = 1 \\
&\Leftrightarrow \dfrac{x}{2}=\text{e}\\
&\Leftrightarrow x=2\text{e}
\end{align*}$
De même :
$\begin{align*} 1-\ln \left(\dfrac{x}{2}\right) > 0 &\Leftrightarrow \ln \left(\dfrac{x}{2}\right) < 1 \\
&\Leftrightarrow \dfrac{x}{2}<\text{e} \\
&\Leftrightarrow x<2\text{e}
\end{align*}$
Ainsi la fonction $\mathscr{A}$ admet un maximum pour $x=2\text{e}$.
$f\left(2\text{e}\right)=2-\ln\left(\dfrac{2e}{2}\right)=2-\ln \text{e} = 1$.
Par conséquent l’aire du rectangle $OPMQ$ n’est pas constante. Elle peut être maximale. Cela se produit pour $M(2\text{e};1)$
$\quad$
Spécialité 5 points
Partie A
On considère les matrices $M$ de la forme $M = \begin{pmatrix}a&b\\5&3\end{pmatrix}$ où $a$ et $b$ sont des nombres entiers. Le nombre $3a - 5b$ est appelé le déterminant de $M$. On le note det$(M)$. Ainsi det$(M) = 3a - 5b$.
- Dans cette question on suppose que det$(M) \ne 0$ et on pose $N = \dfrac{1}{\text{det}(M)}\begin{pmatrix}3&- b\\- 5&a\end{pmatrix}$. Justifier que $N$ est l'inverse de $M$.
- On considère l'équation $(E) :\quad \text{det}(M) = 3$. On souhaite déterminer tous les couples d'entiers $(a~;~b)$ solutions de l'équation $(E)$.
- Vérifier que le couple $(6~;~3)$ est une solution de $(E)$.
- Montrer que le couple d'entiers $(a~;~b)$ est solution de $(E)$ si et seulement si $3(a - 6) = 5(b - 3)$. En déduire l'ensemble des solutions de l'équation $(E)$.
Partie B
- On pose $Q = \begin{pmatrix}6 &3\\ 5& 3\end{pmatrix}$. En utilisant la partie A, déterminer la matrice inverse de $Q$.
- Codage avec la matrice $Q$ Pour coder un mot de deux lettres à l'aide de la matrice $Q = \begin{pmatrix}6 &3\\ 5& 3\end{pmatrix}$ on utilise la procédure ci-après :
Étape 1 : On associe au mot la matrice $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ où $x_1$ est l'entier correspondant à la première lettre du mot et $x_2$ l'entier correspondant à la deuxième lettre du mot selon le tableau de correspondance ci-dessous : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12\\ \hline\hline N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\ \hline 13&14&15&16&17&18&19&20&21&22&23&24&25\\ \hline \end{array} $$
Étape 2 : La matrice $X$ est transformée en la matrice $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ telle que $Y = QX$.
Étape 3 : La matrice $Y$ est transformée en la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$ telle que $r_1$ est le reste de la division euclidienne de $y_1$ par 26 et $r_2$ est le reste de la division euclidienne de $y_2$ par 26.
Étape 4 : À la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$ on associe un mot de deux lettres selon le tableau de correspondance de l'étape 1. \[\text{Exemple :} \text{JE} \to X = \begin{pmatrix}9\\4\end{pmatrix} \to Y = \begin{pmatrix}66\\57\end{pmatrix} \to R = \begin{pmatrix}14\\5\end{pmatrix} \to \text{OF}.\] Le mot JE est codé en le mot OF. Coder le mot DO. - Procédure de décodage On conserve les mêmes notations que pour le codage. Lors du codage, la matrice $X$ a été transformée en la matrice $Y$ telle que $Y = QX$.
- Démontrer que $3X = 3Q^{-1}Y$ puis que $\left\{\begin{array}{l c r} 3x_1&=&3r_1 - 3r_2 \quad [26]\\ 3x_2&=&-5r_1 + 6r_2 \quad [26] \end{array}\right.$
- En remarquant que $9 \times 3 \equiv 1 \quad [26]$, montrer que $\left\{\begin{array}{l c r} x_1&\equiv& r_1 - r_2 \quad [26]\\ x_2&\equiv& 7r_1 + 2r_2 \quad [26] \end{array}\right.$
- Décoder le mot SG.
Correction de l'exercice de Spécialité 5 points
Partie A
On considère les matrices $M$ de la forme $M = \begin{pmatrix}a&b\\5&3\end{pmatrix}$ où $a$ et $b$ sont des nombres entiers. Le nombre $3a - 5b$ est appelé le déterminant de $M$. On le note det$(M)$. Ainsi det$(M) = 3a - 5b$.
- Dans cette question on suppose que det$(M) \ne 0$ et on pose $N = \dfrac{1}{\text{det}(M)}\begin{pmatrix}3&- b\\- 5&a\end{pmatrix}$. Justifier que $N$ est l'inverse de $M$. $\begin{align*} N\times M&=\dfrac{1}{3a-5b}\begin{pmatrix}3&-b\\-5&a\end{pmatrix} \begin{pmatrix}a&b\\5&3\end{pmatrix} \\
- On considère l'équation $(E) :\quad \text{det}(M) = 3$. On souhaite déterminer tous les couples d'entiers $(a~;~b)$ solutions de l'équation $(E)$.
- Vérifier que le couple $(6~;~3)$ est une solution de $(E)$. $3\times 6-5\times 3=18-15=3$.
- Montrer que le couple d'entiers $(a~;~b)$ est solution de $(E)$ si et seulement si $3(a - 6) = 5(b - 3)$. En déduire l'ensemble des solutions de l'équation $(E)$. On considère un autre couple d’entiers solutions $(a;b)$.
Donc le couple $(6;3)$ est bien solution de l’équation det$(M)=3$.
$\quad$
On a donc $3a-5b=3$ et $3\times 6-5\times 3=3$.
Par soustraction, on obtient : $3a-3\times 6-5b+5\times 3 = 0$
Soit $3(a-6)=5(b-3)$.
Donc si $(a;b)$ est solution de l’équation alors $3(a-6)=5(b-3)$.
$\quad$
Réciproquement si $3(a-6)=5(b-3)$
Alors $3a-18=5b-15 \Leftrightarrow 3a-5b=3$ et $(a;b)$ est solution de l’équation $(E)$.
$\quad$
Ainsi $(a;b)$ est solution de l’équation $(E)$ si, et seulement si, $3(a-6)=5(b-3)$.
$\quad$
$5$ et $3$ sont premiers entre eux.
D’après le théorème de Gauss, il existe donc un entier relatif $k$ tel que :
$a-6=5k$ et $b-3=3k$.
Soit $a=6+5k$ et $b=3+3k$.
$\quad$Réciproquement, soit $k\in \mathbb Z$. Alors :
$3(6+5k)-5(3+3k) = 18+15k-15-15k=3$.
Donc le couple $(6+5k;3+3k)$ est solution de l’équation $(E)$.
$\quad$
&=\dfrac{1}{3a-5b}\begin{pmatrix}3a-5b&3b-3b\\-5a+5a&-5b+3a\end{pmatrix} \\
&=\begin{pmatrix} 1&0\\0&1\end{pmatrix}
\end{align*}$
Par conséquent $N$ est bien l’inverse de $M$.
$\quad$
Partie B
- On pose $Q = \begin{pmatrix}6 &3\\ 5& 3\end{pmatrix}$. En utilisant la partie A, déterminer la matrice inverse de $Q$. det$(Q) =3\times 6-3\times 5=3$.
- Codage avec la matrice $Q$ Pour coder un mot de deux lettres à l'aide de la matrice $Q = \begin{pmatrix}6 &3\\ 5& 3\end{pmatrix}$ on utilise la procédure ci-après :
Étape 1 : On associe au mot la matrice $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ où $x_1$ est l'entier correspondant à la première lettre du mot et $x_2$ l'entier correspondant à la deuxième lettre du mot selon le tableau de correspondance ci-dessous : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12\\ \hline\hline N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\ \hline 13&14&15&16&17&18&19&20&21&22&23&24&25\\ \hline \end{array} $$
Étape 2 : La matrice $X$ est transformée en la matrice $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ telle que $Y = QX$.
Étape 3 : La matrice $Y$ est transformée en la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$ telle que $r_1$ est le reste de la division euclidienne de $y_1$ par 26 et $r_2$ est le reste de la division euclidienne de $y_2$ par 26.
Étape 4 : À la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$ on associe un mot de deux lettres selon le tableau de correspondance de l'étape 1. \[\text{Exemple :} \text{JE} \to X = \begin{pmatrix}9\\4\end{pmatrix} \to Y = \begin{pmatrix}66\\57\end{pmatrix} \to R = \begin{pmatrix}14\\5\end{pmatrix} \to \text{OF}.\]Le mot JE est codé en le mot OF. Coder le mot DO.DO$\rightarrow X=\begin{pmatrix}3\\14\end{pmatrix}$
$Y=QX=\begin{pmatrix}60\\57\end{pmatrix}$
Or $60 \equiv 8~[26]$ et $57\equiv 5~[26]$.
Donc $R=\begin{pmatrix}8\\5\end{pmatrix}$
Le mot DO est donc codé en IF
$\quad$ - Procédure de décodage On conserve les mêmes notations que pour le codage. Lors du codage, la matrice $X$ a été transformée en la matrice $Y$ telle que $Y = QX$.
- Démontrer que $3X = 3Q^{-1}Y$ puis que $\left\{\begin{array}{l c r} 3x_1&=&3r_1 - 3r_2 \quad [26]\\ 3x_2&=&-5r_1 + 6r_2 \quad [26] \end{array}\right.$ det$(Q) =3\times 6-3\times 5=3$.
- En remarquant que $9 \times 3 \equiv 1 \quad [26]$, montrer que $\left\{\begin{array}{l c r} x_1&\equiv& r_1 - r_2 \quad [26]\\ x_2&\equiv& 7r_1 + 2r_2 \quad [26] \end{array}\right.$ $9\times 3 = 27 = 1+26$ donc $9\times 3\equiv 1~[26]$.
- Décoder le mot SG. SG$\rightarrow R=\begin{pmatrix}18\\6\end{pmatrix}$
$3Q^{-1}Y=3Q^{-1}QX=3X$
Par conséquent $\begin{cases} 3x_1=3y_1-3y_2\\3x_2=-5y_1+6y_2\end{cases}$
En passant au modulo, on obtient alors :
$\begin{cases} 3x_1\equiv 3r_1-3r_2~[26]\\3x_2\equiv -5r_1+6r_2~[26] \end{cases}$
$\quad$
On multiplie chacune des équations du système précédent par $9$.
On obtient alors :
$\begin{cases} x_1\equiv r_1-r_2~[26]\\x_2\equiv -45r_1+54r_2~[26] \end{cases}$
soit
$\begin{cases} x_1\equiv r_1-r_2~[26]\\x_2\equiv 7r_1+2r_2~[26] \end{cases}$
$\quad$
Donc $\begin{cases} x_1\equiv 18-6~[26]\\x_2\equiv 7\times 18+2\times 6~[26] \end{cases}$ $\Leftrightarrow \begin{cases}x_1\equiv 12~[26]\\x_2\equiv 138~[26]\end{cases}$ $\Leftrightarrow \begin{cases} x_1\equiv 12~[26]\\x_2\equiv 8~[26] \end{cases}$
Ainsi le mot initial était MI.
Ainsi l’inverse de $Q$ est $Q^{-1}=\dfrac{1}{3}\begin{pmatrix}3&-3\\-5&6\end{pmatrix}$.
$\quad$ En vidéo !
Exercice 5 5 points
On souhaite stériliser une boîte de conserve. Pour cela, on la prend à la température ambiante $T_0 = 25$degrés C et on la place dans un four à température constante $T_F = 100$degrés C. La stérilisation débute dès lors que la température de la boîte est supérieure à 85degrés C.
Les deux parties de cet exercice sont indépendantes
Partie A : Modélisation discrète
Pour $n$ entier naturel, on note $T_n$ la température en degré Celsius de la boîte au bout de $n$ minutes. On a donc $T_0 = 25$. Pour $n$ non nul, la valeur $T_n$ est calculée puis affichée par l'algorithme suivant : $$\begin{array}{ |l|l|}\hline \text{Initialisation :} & T \text{ prend la valeur 25}\\ \hline \text{ Traitement :} & \text{ Demander la valeur de } n \\ & \text{ Pour } i \text{ allant de } 1 \text{ à } n \text{ faire}\\ &\hspace{0,5cm} T \text{ prend la valeur } 0,85 \times T + 15 \\ & \text{ Fin Pour }\\ \hline \text{ Sortie :} & \text{ Afficher }T\\ \hline \end{array} $$
- Déterminer la température de la boîte de conserve au bout de 3 minutes. Arrondir à l'unité.
- Démontrer que, pour tout entier naturel $n$, on a $T_n = 100 - 75 \times 0,85^n$.
- Au bout de combien de minutes la stérilisation débute-elle ?
Partie B : Modélisation continue
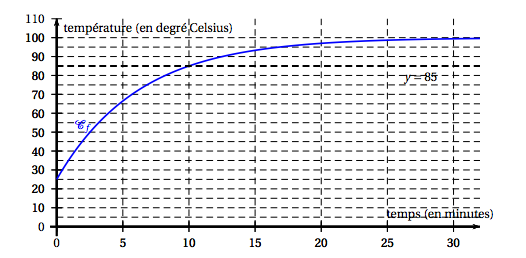
Dans cette partie, $t$ désigne un réel positif. On suppose désormais qu'à l'instant $t$ (exprimé en minutes), la température de la boîte est donnée par $f(t)$ (exprimée en degré Celsius) avec : \[f(t) = 100 - 75\text{e}^{- \frac{\ln 5}{10}t}.\]
-
- Étudier le sens de variations de $f$ sur $[0~;~+ \infty[$.
- Justifier que si $t \geqslant 10$ alors $f(t) \geqslant 85$.
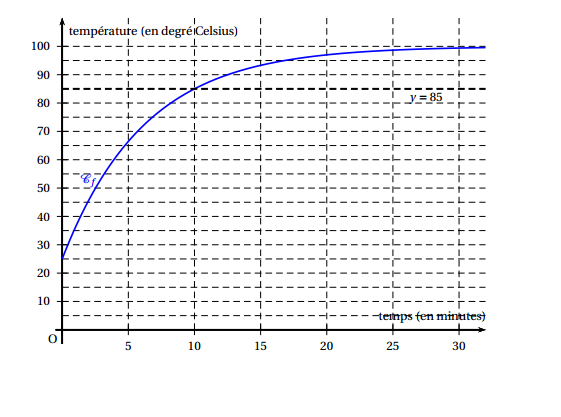
- Soit $\theta$ un réel supérieur ou égal à 10. On note $\mathcal{A}(\theta)$ le domaine délimité par les droites d'équation $t = 10,\: t = \theta,\:$ $y = 85$ et la courbe représentative $\mathcal{C}_f$ de $f$. On considère que la stérilisation est finie au bout d'un temps $\theta$, si l'aire, exprimée en unité d'aire du domaine $\mathcal{A}(\theta)$ est supérieure à $80$.
- Justifier, à l'aide du graphique donné en annexe , que l'on a $\mathcal{A}(25) > 80$.
- Justifier que, pour $\theta \geqslant 10$, on a $\mathcal{A}(\theta) = 15(\theta - 10) - 75 \displaystyle\int_{10}^{\theta} \text{e}^{- \frac{\ln 5}{10}t}\:\text{d}t$.
- La stérilisation est-elle finie au bout de 20 minutes ?
Correction Exercice 5 5 points
On souhaite stériliser une boîte de conserve. Pour cela, on la prend à la température ambiante $T_0 = 25$degrés C et on la place dans un four à température constante $T_F = 100$degrés C. La stérilisation débute dès lors que la température de la boîte est supérieure à 85degrés C.
Les deux parties de cet exercice sont indépendantes
Partie A : Modélisation discrète
Pour $n$ entier naturel, on note $T_n$ la température en degré Celsius de la boîte au bout de $n$ minutes. On a donc $T_0 = 25$. Pour $n$ non nul, la valeur $T_n$ est calculée puis affichée par l'algorithme suivant : $$\begin{array}{ |l|l|}\hline \text{Initialisation :} & T \text{ prend la valeur 25}\\ \hline \text{ Traitement :} & \text{ Demander la valeur de } n \\ & \text{ Pour } i \text{ allant de } 1 \text{ à } n \text{ faire}\\ &\hspace{0,5cm} T \text{ prend la valeur } 0,85 \times T + 15 \\ & \text{ Fin Pour }\\ \hline \text{ Sortie :} & \text{ Afficher }T\\ \hline \end{array} $$
- Déterminer la température de la boîte de conserve au bout de 3 minutes. Arrondir à l'unité. $T_0=25$, $T_1=36,25$, $T_2=45,8125$ et $T_3=53,940625$.
- Démontrer que, pour tout entier naturel $n$, on a $T_n = 100 - 75 \times 0,85^n$. Montrons par récurrence que, pour tout entier naturel $n$ on a $T_n=100-75\times 0,85^n$.
- Au bout de combien de minutes la stérilisation débute-elle ? La stérilisation débute quand $T_n>85$.
Ainsi la température de la boîte arrondie à l’unité est de $54$°C.
$\quad$
Initialisation : Si $n=0$, $T_0=25$ et $100-75\times 0,85^0=100-75=25$.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $T_n=100-75\times 0,85^n$.
$\begin{align*} T_{n+1}&=0,85 \times T_n+15 \\
&=0,85 \times \left(100-75\times 0,85^n\right)+15 \\
&=85-75\times 0,85^{n+1}+15 \\
&=100-75\times 0,85^{n+1}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est donc vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, $T_n=100-75\times 0,85^n$.
$\quad$
On résout donc :
$\begin{align*} 100-75\times 0,85^n > 85 &\Leftrightarrow -75\times 0,85^n > -15 \\
&\Leftrightarrow 0,85^n < 0,2 \\
&\Leftrightarrow n\ln 0,85 < \ln 0,2 \\
&\Leftrightarrow n> \dfrac{\ln 0,2}{\ln 0,85}
&\Leftrightarrow n \geqslant 10
\end{align*}$
La stérilisation commence donc au bout de $10$ minutes.
$\quad$
Partie B : Modélisation continue
Dans cette partie, $t$ désigne un réel positif. On suppose désormais qu'à l'instant $t$ (exprimé en minutes), la température de la boîte est donnée par $f(t)$ (exprimée en degré Celsius) avec : \[f(t) = 100 - 75\text{e}^{- \frac{\ln 5}{10}t}.\]
-
- Étudier le sens de variations de $f$ sur $[0~;~+ \infty[$. $f$ est une fonction dérivable sur $[0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
- Justifier que si $t \geqslant 10$ alors $f(t) \geqslant 85$.
$f'(t)=75\times \dfrac{\ln 5}{10}\text{e}^{-\frac{\ln 5}{10}t} > 0$ car la fonction exponentielle est toujours strictement positive.
Donc $f$ est strictement croissante sur $[0;+\infty[$.
$\quad$
Puisque la fonction $f$ est strictement croissante sur $[0;+\infty[$, alors, pour tout $t\geqslant 10$ alors $f(t) \geqslant f(10)$ soit $f(t)\geqslant 85$.
$\quad$ - Soit $\theta$ un réel supérieur ou égal à 10. On note $\mathcal{A}(\theta)$ le domaine délimité par les droites d'équation $t = 10,\: t = \theta,\:$ $y = 85$ et la courbe représentative $\mathcal{C}_f$ de $f$. On considère que la stérilisation est finie au bout d'un temps $\theta$, si l'aire, exprimée en unité d'aire du domaine $\mathcal{A}(\theta)$ est supérieure à $80$.
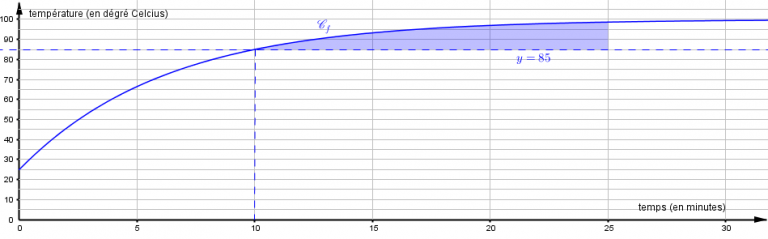
- Justifier, à l'aide du graphique donné en annexe , que l'on a $\mathcal{A}(25) > 80$. Chaque rectangle a une aire de $5\times 5$ unités d’aires.
- Justifier que, pour $\theta \geqslant 10$, on a $\mathcal{A}(\theta) = 15(\theta - 10) - 75 \displaystyle\int_{10}^{\theta} \text{e}^{- \frac{\ln 5}{10}t}\:\text{d}t$. $\begin{align*} A(\theta)&=\displaystyle \int_{10}^{\theta} (f(t)-85)\mathrm{d}t \\
- La stérilisation est-elle finie au bout de 20 minutes ? $\begin{align*} \int_{10}^{\theta}\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t &=- \dfrac{10}{\ln 5}\left[\text{e}^{-\frac{\ln 5}{10}t}\right]_{10}^{\theta} \\
$3$ rectangles complets sont inclus dans la partie coloriée et en prenant deux des morceaux de rectangles restants on obtient une aire supérieure à celle d’un quatrième rectangle.
L’aire coloriée est donc supérieure ou égale à $4\times 5\times 5 = 100 > 80$.
Donc $A(25)>80$.
&=\int_{10}^{\theta}\left(15-75\text{e}^{-\frac{\ln 5}{10}t}\right)\mathrm{d}t \\
&=\int_{10}^{\theta}15\mathrm{d}t-\int_{10}^{\theta}75\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t \\
&=15(\theta-10)-\int_{10}^{\theta}75\text{e}^{-\frac{\ln 5}\\{10}t}\mathrm{d}t \\
&=15(\theta-10)-75\int_{10}^{\theta}\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t
\end{align*}$
&=-\dfrac{10}{\ln 5}\left(\text{e}^{-\frac{\ln 5}{10}\theta}-\dfrac{1}{5}\right)
\end{align*}$
Ainsi $A(20)=150 + 75\times \dfrac{10}{\ln 5}\left(\text{e}^{-\frac{\ln 5}{10}\times 20}-\dfrac{1}{5}\right) \approx 75,4 <80$.
La stérilisation n’est donc pas terminée au bout de $20$ minutes.
Annexes
- Vues: 34773
