Baccalauréat S Pondichéry 22 avril 2016 - Correction Exercice 2

Page 4 sur 13: Correction Exercice 2

Correction de l'exercice 2 (3 points)

Commun à tous les candidats

L'objectif de cet exercice est de trouver une méthode pour construire à la règle et au compas un pentagone régulier.
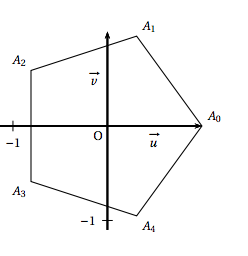
Dans le plan complexe muni d'un repère orthonormé direct $(O; \vec {u}, \vec{v})$, on considère le pentagone régulier $A_0A_1A_2A_3A_4$, de centre $O$ tel que $\vec{OA_0} = \vec{u}$. On rappelle que dans le pentagone régulier $A_0A_1A_2A_3A_4$, ci-contre :

• les cinq côtés sont de même longueur;
• les points $A_0,\:A_1,\:A_2,\:A_3$ et $A_4$ appartiennent au cercle trigonométrique ;
• pour tout entier $k$ appartenant à $\{0~;~1~;~2~;~3\}$ on a $\left(\vec{OA_k}~;~\vec{OA_{k+1}}\right) = \dfrac{2\pi}{5}$.

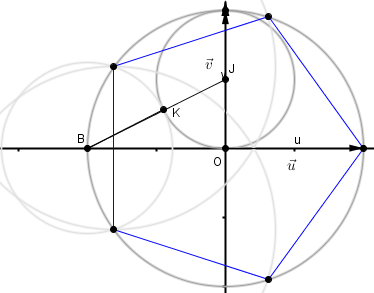
1. On considère les points $B$ d'affixe $- 1$ et $J$ d'affixe $\dfrac{\text{i}}{2}$. Le cercle $(\mathcal{C})$ de centre $J$ et de rayon $\dfrac{1}{2}$ coupe le segment $[BJ]$ en un point $K$. Calculer $BJ$, puis en déduire $BK$.
$BJ=\left|\dfrac{\text{i}}{2}+1\right| = \sqrt{\dfrac{5}{4}}=\dfrac{\sqrt{5}}{2}$
$B, K$ et $J$ sont alignés dans cet ordre. Donc $BK=BJ-\dfrac{1}{2}=\dfrac{\sqrt{5}-1}{2}$.
$\quad$
1. Donner sous forme exponentielle l'affixe du point $A_2$. Justifier brièvement.
On appelle $z_2$ l’affixe de $A_2$. $A_2$ appartient au cercle trigonométrique donc $\left|z_2\right|=1$.
$arg\left(z_2\right)=2\times \dfrac{2\pi}{5}=\dfrac{4\pi}{5}$.
Ainsi $z_2=\text{e}^{4\text{i}\pi/5}$.
$\quad$

2. Démontrer que $BA_2\,^2 = 2 + 2\cos \left(\dfrac{4\pi}{5}\right)$.
$\begin{align*} BA_2 ^2 &= \left|z_2+1\right|^2 \\
&=\left|\cos\left(\dfrac{4\pi}{5}\right)+1+\text{i}\sin \left(\dfrac{4\pi}{5}\right)\right|^2 \\
&=\left(1+\cos\left(\dfrac{4\pi}{5}\right)\right)^2+\left(\sin\left(\dfrac{4\pi}{5}\right)\right)^2 \\
&=1+2\cos\left(\dfrac{4\pi}{5}\right)+\left(\cos\left(\dfrac{4\pi}{5}\right)\right)^2+\left(\sin\left(\dfrac{4\pi}{5}\right)\right)^2 \\
&=2+2\cos\left(\dfrac{4\pi}{5}\right)
\end{align*}$
$\quad$

Un logiciel de calcul formel affiche les résultats ci-dessous, que l'on pourra utiliser sans justification : $$\begin{array}{|c|c|}\hline \blacktriangleright \text{ Calcul formel}\\\hline 1&cos (4*pi/5)\\ & \to \dfrac{1}{4}\left(- \sqrt{5} - 1\right) \\ \hline 2& sqrt((3 - sqrt(5))/2)\\ \hline & \to \dfrac{1}{2}\left(\sqrt{5} - 1\right) \\ \hline \end{array}$$ « sqrt » signifie « racine carrée» En déduire, grâce à ces résultats, que $BA_2 = BK$.

$\begin{align*} BA_2 ^2 &= 2+2\times\dfrac{1}{4}\left(-\sqrt{5}-1\right) \\
&=\dfrac{4-\sqrt{5}-1}{2} \\
&=\dfrac{3-\sqrt{5}}{2}
\end{align*}$
Par conséquent $BA_2=\sqrt{\dfrac{3-\sqrt{5}}{2}}=\dfrac{\sqrt{5}-1}{2}=BK$
$\quad$

Dans le repère $(O; \vec {u}, \vec{v})$ donné en annexe, construire à la règle et au compas un pentagone régulier.
N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.

On place le point $B$ et le point $J$.
A l’aide des graduation fournie on trace le cercle de centre $J$ et de rayon $0.5$, ce qui permet de placer le point $K$.
On trace le cercle de centre $O$ et de rayon $1$ et on repporte à partir de $B$ la distance $BK$ sur ce cercle, ce qui permet de trouver les points $A_2$ et $A_3$.
On possède maintenant deux points consécutifs de ce pentagone régulier, ce qui permet de placer les autres points en reportant la distance les séparant sur le cercle trigonométrique.
$\quad$