Baccalauréat S Liban 31 mai 2016 - Correction Exercice 3

Page 6 sur 12: Correction Exercice 3

Correction de l'exercice 3 (4 points)

Commun à tous les candidats

Fonctions et calcul intégral

On considère la fonction $f$ définie sur l'intervalle [0 ; 1] par : \[f(x) = \dfrac{1}{1 + \text{e}^{1 - x}}.\]

Partie A

 

1. Étudier le sens de variation de la fonction $f$ sur l'intervalle [0 ; 1].
$f$ est un quotient de fonctions dérivables sur $[0;1]$ dont le dénominateur ne s’annule pas (puisque la fonction exponentielle est strictement positive). Elle est donc également dérivable sur cet intervalle.
Ainsi $f'(x)=-\dfrac{-\text{e}^{1-x}}{\left(1+\text{e}^{1-x}\right)^2}$ $= \dfrac{\text{e}^{1-x}}{\left(1+\text{e}^{1-x}\right)^2}$.
La fonction exponentielle étant positive, pour tout réel $x\in[0;1]$ on a donc $f'(x) > 0$.
La fonction $f$ est donc croissante sur $[0;1]$.

2. Démontrer que pour tout réel $x$ de l'intervalle [0;1], $f(x) = \dfrac{\text{e}^x}{\text{e}^x + \text{e}}$ (on rappelle que $\text{e} = \text{e}^1$).
$\begin{align*} f(x)&=\dfrac{1}{1+\text{e}^{1-x}} \\
&=\dfrac{1}{1+\text{e}^{1-x}} \times \dfrac{e^x}{e^x}\\
&=\dfrac{\text{e}^x}{\text{e}^x+\text{e}}
\end{align*}$

3. Montrer alors que $\displaystyle\int_0^1 f(x)\:\text{d}x = \ln (2) + 1 - \ln (1 + \text{e})$.
On a ainsi :
$$\begin{align*} \int_0^1f(x)\mathrm{d}x &= \Big[\ln\left(\text{e}^x+\text{e}e\right)\Big]_0^1 \\
&= \ln(2\text{e})-\ln(1+\text{e}) \\
&=\ln(2)+\ln(\text{e})-\ln(1+\text{e})\\
&=\ln(2)+1-\ln(1+\e)
\end{align*}$$

 

Partie B

Soit $n$ un entier naturel. On considère les fonctions $f_n$ définies sur [0;1] par: \[f_n(x) = \dfrac{1}{1 + n\text{e}^{1 - x}}.\] On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans le plan muni d'un repère orthonormé. On considère la suite de terme général \[u_n = \displaystyle\int_0^1 f_n(x)\:\text{d}x.\]

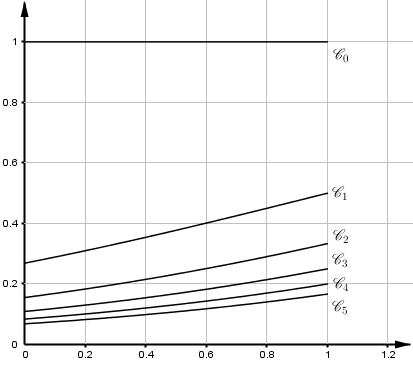
1. On a tracé en annexe les courbes représentatives des fonctions $f_n$ pour $n$ variant de 1 à 5. Compléter le graphique en traçant la courbe $\mathcal{C}_0$ représentative de la fonction $f_0$.
$f_0(x)=1$ pour tout $x\in[0;1]$.

2. Soit $n$ un entier naturel, interpréter graphiquement $u_n$ et préciser la valeur de $u_0$.
$u_n$ correspond à l’aire du domaine compris entre la courbe $\mathscr{C}_n$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$.
Puisque la fonction $f_0$ est constante sur $[0;1]$ alors $u_0=1\times 1=1$.

3. Quelle conjecture peut-on émettre quant au sens de variation de la suite $\left(u_n\right)$ ? Démontrer cette conjecture.
La suite $\left(u_n\right)$ semble être décroissante.
$\quad$
$\begin{align*} u_{n+1}-u_{n} &=\displaystyle \int_0^1 \dfrac{1}{1+(n+1)\text{e}^{1-x}}\mathrm{d}x-\int_0^1 \dfrac{1}{1+n\text{e}^{1-x}}\mathrm{d}x \\
&= \int_0^1 \left(\dfrac{1}{1+(n+1)\text{e}^{1-x}}-\dfrac{1}{1+n\text{e}^{1-x}}\right) \mathrm{d}x \\
&= \int_0^1 \dfrac{1+ne^{1-x}-1-(n+1)\text{e}^{1-x}}{\left(1+(n+1)\text{e}^{1-x}\right)\left(1+n\text{e}^{1-x}\right)} \mathrm{d}x\\
&=\int_0^1 \dfrac{-\text{e}^{1-x}}{\left(1+(n+1)\text{e}^{1-x}\right)\left(1+n\text{e}^{1-x}\right)} \mathrm{d}x
\end{align*}$
Du fait de la positivité de l’exponentielle, $u_{n+1}-u_{n}<0$ et la suite est bien décroissante.

4. La suite $\left(u_n\right)$ admet-elle une limite ?
Pour tout $n$ on a $u_n > 0$ comme intégrale d’une fonction continue strictement positive sur $[0;1]$.
La suite $\left(u_n\right)$ est donc décroissante et minorée par $0$. Elle est par conséquent convergente et possède ainsi une limite.