Baccalauréat S Amérique du Nord 1er juin 2016
Exercice 1 6 points
Une entreprise fabrique des billes en bois sphériques grâce à deux machines de production A et B. L'entreprise considère qu'une bille peut être vendue uniquement lorsque son diamètre est compris entre 0,9 cm et 1,1 cm. Les parties A, B et C sont indépendantes.
Partie A
Une étude du fonctionnement des machines a permis d'établir les résultats suivants :
- 96% de la production journalière est vendable.
- La machine A fournit 60% de la production journalière.
- La proportion de billes vendables parmi la production de la machine A est 98%.
On choisit une bille au hasard dans la production d'un jour donné. On définit les évènements suivants :
$A$ : «la bille a été fabriquée par la machine A » ;
$B$ : «la bille a été fabriquée par la machine B » ; $V$ : «la bille est vendable ».
- Déterminer la probabilité que la bille choisie soit vendable et provienne de la machine A.
- Justifier que $P(B \cap V) = 0,372$ et en déduire la probabilité que la bille choisie soit vendable sachant qu'elle provient de la machine B.
- Un technicien affirme que 70% des billes non vendables proviennent de la machine B. A-t-il raison ?
Partie B
Dans cette partie, on s'intéresse au diamètre, exprimé en cm, des billes produites par les machines A et B.
- Une étude statistique conduit à modéliser le diamètre d'une bille prélevée au hasard dans la production de la machine B par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 1$ et d'écart-type $\sigma = 0,055$. Vérifier que la probabilité qu'une bille produite par la machine B soit vendable est bien celle trouvée dans la partie A, au centième près.
- De la même façon, le diamètre d'une bille prélevée au hasard dans la production de la machine A est modélisé à l'aide d'une variable aléatoire $Y$ qui suit une loi normale d'espérance $\mu = 1$ et d'écart-type $\sigma',\: \sigma'$ étant un réel strictement positif. Sachant que $P(0,9 \leqslant Y \leqslant 1,1) = 0,98$, déterminer une valeur approchée au millième de $\sigma'$.
Partie C
Les billes vendables passent ensuite dans une machine qui les teinte de manière aléatoire et équiprobable en blanc, noir, bleu, jaune ou rouge. Après avoir été mélangées, les billes sont conditionnées en sachets. La quantité produite est suffisamment importante pour que le remplissage d'un sachet puisse être assimilé à un tirage successif avec remise de billes dans la production journalière. Une étude de consommation montre que les enfants sont particulièrement attirés par les billes de couleur noire.
- Dans cette question seulement, les sachets sont tous composés de 40 billes.
- On choisit au hasard un sachet de billes. Déterminer la probabilité que le sachet choisi contienne exactement $10$ billes noires. On arrondira le résultat à $10^{-3}$.
- Dans un sachet de $40$ billes, on a compté $12$ billes noires. Ce constat permet-t-il de remettre en cause le réglage de la machine qui teinte les billes ?
- Si l'entreprise souhaite que la probabilité d'obtenir au moins une bille noire dans un sachet soit supérieure ou égale à 99%, quel nombre minimal de billes chaque sachet doit-il contenir pour atteindre cet objectif ?
Correction de l'exercice 1 (6 points)
Une entreprise fabrique des billes en bois sphériques grâce à deux machines de production A et B. L'entreprise considère qu'une bille peut être vendue uniquement lorsque son diamètre est compris entre 0,9 cm et 1,1 cm. Les parties A, B et C sont indépendantes.
Partie A
Une étude du fonctionnement des machines a permis d'établir les résultats suivants :
- 96% de la production journalière est vendable.
- La machine A fournit 60% de la production journalière.
- La proportion de billes vendables parmi la production de la machine A est 98%.
On choisit une bille au hasard dans la production d'un jour donné. On définit les évènements suivants :
$A$ : «la bille a été fabriquée par la machine A » ;
$B$ : «la bille a été fabriquée par la machine B » ; $V$ : «la bille est vendable ».
- Déterminer la probabilité que la bille choisie soit vendable et provienne de la machine A. On a $P(A)=0,6$ et $P_A(V)=0,98$
- Justifier que $P(B \cap V) = 0,372$ et en déduire la probabilité que la bille choisie soit vendable sachant qu'elle provient de la machine B. D’après la formule des probabilités totales on a :
- Un technicien affirme que 70% des billes non vendables proviennent de la machine B. A-t-il raison ? On veut calculer $P(_{\overline{V}}(B)=\dfrac{P\left(\overline{V}\cap B\right)}{P\left(\overline{V}\right)}$.
Donc $P(A\cap V) = P(A) \times P_A(V)=0,6\times 0,98 = 0,588$.
$\quad$
$\begin{align*} P(V)&=P(A\cap V)+P(B\cap V) \\
0,96&=0,588+P(B\cap V)
\end{align*}$
Donc $P(B\cap V)=0,96-0,588=0,372$.
$\quad$
On sait que $P\left(\overline{V}\right) = 1-P(V)=0,04$.
Puisque $P(V\cap B)=0,372$ et $P(B)=0,4$ alors $P_B(V)=\dfrac{P(V\cap B)}{P(B)}=\dfrac{0,372}{0,4}=0,93$.
Ainsi $P_B\left(\overline{V}\right) = 1-0,93=0,07$.
Donc $P\left(\overline{V}\cap B\right)=P_B\left(\overline{V}\right) \times P(B)=0,07\times 0,4=0,028$.
Par conséquent $P(_{\overline{V}}(B)=\dfrac{P\left(\overline{V}\cap B\right)}{P\left(\overline{V}\right)} = \dfrac{0,028}{0,04}=0,7$.
Le technicien a donc raison.
$\quad$
Partie B
Dans cette partie, on s'intéresse au diamètre, exprimé en cm, des billes produites par les machines A et B.
- Une étude statistique conduit à modéliser le diamètre d'une bille prélevée au hasard dans la production de la machine B par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 1$ et d'écart-type $\sigma = 0,055$. Vérifier que la probabilité qu'une bille produite par la machine B soit vendable est bien celle trouvée dans la partie A, au centième près. On veut calculer $P(0,9\leqslant X \leqslant 1,1) \approx 0,93$
- De la même façon, le diamètre d'une bille prélevée au hasard dans la production de la machine A est modélisé à l'aide d'une variable aléatoire $Y$ qui suit une loi normale d'espérance $\mu = 1$ et d'écart-type $\sigma',\: \sigma'$ étant un réel strictement positif. Sachant que $P(0,9 \leqslant Y \leqslant 1,1) = 0,98$, déterminer une valeur approchée au millième de $\sigma'$. On a :
On retrouve bien la valeur de $P_B(V)$ trouvée à la question A.3.
$\quad$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
En vidéo !
$\begin{align*} P(0,9 \leqslant Y \leqslant 1,1)=0,98 &\iff P(-0,1 \leqslant Y-1 \leqslant 0,1)=0,98 \\
&\iff P\left(-\dfrac{0,1}{\sigma’} \leqslant \dfrac{Y-1}{\sigma’} \leqslant \dfrac{0,1}{\sigma’}\right)=0,98
\end{align*}$
Or la variable aléatoire $Y’=\dfrac{Y-1}{\sigma’}$ suit la loi normale centrée réduite.
Ainsi :
$\begin{align*} P\left(-\dfrac{0,1}{\sigma’} \leqslant \dfrac{Y-1}{\sigma’} \leqslant \dfrac{0,1}{\sigma’}\right)=0,98 &\iff 2P\left(Y’ \leqslant \dfrac{0,1}{\sigma’}\right)-1=0,98 \\
&\iff 2P\left(Y’ \leqslant \dfrac{0,1}{\sigma’}\right) = 1,98 \\
&\iff P\left(Y’ \leqslant \dfrac{0,1}{\sigma’}\right) = 0,99
\end{align*}$
A l’aide de la touche Inverse loi normale de la calculatrice on trouve :
$\dfrac{0,1}{\sigma’} \approx 2,326 \iff \sigma’ \approx 0,043$.
$\quad$
En vidéo !
Partie C
Les billes vendables passent ensuite dans une machine qui les teinte de manière aléatoire et équiprobable en blanc, noir, bleu, jaune ou rouge. Après avoir été mélangées, les billes sont conditionnées en sachets. La quantité produite est suffisamment importante pour que le remplissage d'un sachet puisse être assimilé à un tirage successif avec remise de billes dans la production journalière. Une étude de consommation montre que les enfants sont particulièrement attirés par les billes de couleur noire.
- Dans cette question seulement, les sachets sont tous composés de 40 billes.
- On choisit au hasard un sachet de billes. Déterminer la probabilité que le sachet choisi contienne exactement $10$ billes noires. On arrondira le résultat à $10^{-3}$. On appelle $X$ la variable aléatoire comptant le nombre de billes noires.
- Dans un sachet de $40$ billes, on a compté $12$ billes noires. Ce constat permet-t-il de remettre en cause le réglage de la machine qui teinte les billes ? On a $n=40\geqslant 30$, $p=0,2$ donc $np=8\geqslant 5$ et $n(1-p)=32\geqslant 5$.
Il y a $40$ tirages aléatoires, indépendants avec remise.
A chaque tirage, il y a deux issues $N$ « la bille tirée est noire » et $\overline{N}$.
De plus $P(N)=\dfrac{1}{5}=0,2$ (il y a équiprobabilité des couleurs lors de la teinte).
Donc $X$ suit la loi binomiale de paramètres $n=40$ et $p=0,2$.
a. Ainsi $P(X=10)=\displaystyle \binom{40}{10}\times 0,2^{10}\times 0,8^{30}\approx 0,107$.
$\quad$
En vidéo !
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est alors :
$\begin{align*} I_{40}&=\left[0,2-1,96\sqrt{\dfrac{0,2\times 0,8}{40}};0,2+1,96\sqrt{\dfrac{0,2\times 0,8}{40}}\right]\\
&\approx [0,076;0,324]
\end{align*}$
La fréquence observée est $f=\dfrac{12}{40}=0,3\in I_{40}$.
Cela ne remet donc pas en cause le réglage de la machine qui teinte les billes.
$\quad$ - Si l'entreprise souhaite que la probabilité d'obtenir au moins une bille noire dans un sachet soit supérieure ou égale à 99%, quel nombre minimal de billes chaque sachet doit-il contenir pour atteindre cet objectif ? On appelle $X’$ la variable aléatoire comptant le nombre billes noires parmi $n$ boules tirées.
Pour les mêmes raisons qu’à la question C.1.a. $X’$ suit la loi binomiale de paramètres $n$ et $p=0,2$.
On veut obtenir :
$\begin{align*} P(X’\geqslant 1)\geqslant 0,99 &\iff 1-P(X’=0) \geqslant 0,99 \\
&\iff -P(X’=0) \geqslant -0,01 \\
&\iff P(X’=0) \leqslant 0,01 \\
&\iff 0,8^n \leqslant 0,01 \\
&\iff n\ln(0,8) \leqslant \ln(0,01) \\
&\iff n \geqslant \dfrac{\ln(0,01)}{\ln(0,8)} \\
&\iff n \geqslant 21
\end{align*}$
Il faut donc que les sachets contiennent au moins $21$ billes pour que la probabilité d’obtenir au moins une bille noire dans le sachet soit supérieure à $0,99$.
$\quad$
Exercice 2 6 points
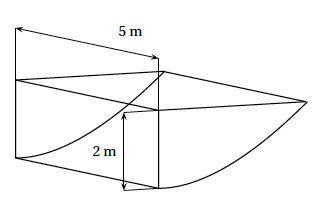
Un particulier veut faire fabriquer un récupérateur d'eau. Ce récupérateur d'eau est une cuve qui doit respecter le cahier des charges suivant :
Cette cuve est schématisée ci-contre. |
|
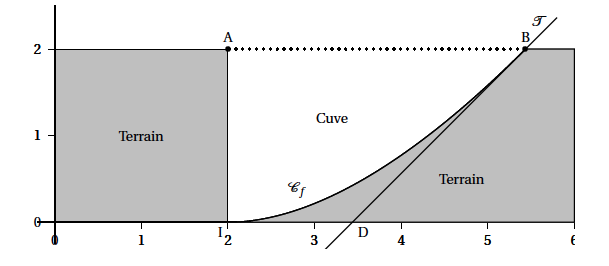
La partie incurvée est modélisée par la courbe $\mathcal{C}_f$ de la fonction $f$ sur l'intervalle $[2~;~2 \text{e}]$ définie par: \[f(x) = x\ln \left( \dfrac{x}{2}\right) - x + 2.\] La courbe $\mathcal{C}_f$ est représentée ci-dessous dans un repère orthonormé d'unité 1 m et constitue une vue de profil de la cuve. On considère les points A(2 ; 2), I(2 ; 0) et B(2e ; 2).
Partie A
L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points B et I appartiennent à la courbe $\mathcal{C}_f$ et que l'axe des abscisses est tangent à la courbe $\mathcal{C}_f$ au point I.
- On note $\mathcal{T}$ la tangente à la courbe $\mathcal{C}_f$ au point B, et D le point d'intersection de la droite $\mathcal{T}$ avec l'axe des abscisses.
- Déterminer une équation de la droite$\mathcal{T}$ et en déduire les coordonnées de D.
- On appelle $S$ l'aire du domaine délimité par la courbe $\mathcal{C}_f$, les droites d'équations $y = 2, x = 2$ et $x = 2\text{e}$. $S$ peut être encadrée par l'aire du triangle ABI et celle du trapèze AIDB. Quel encadrement du volume de la cuve peut-on en déduire ?
-
- Montrer que, sur l'intervalle [2 ;2e], la fonction $G$ définie par \[G(x) = \dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - \dfrac{x^2}{4}\] est une primitive de la fonction $g$ définie par $g(x) = x\ln \left( \dfrac{x}{2}\right)$.
- En déduire une primitive $F$ de la fonction $f$ sur l'intervalle [2 ; 2e].
- Déterminer la valeur exacte de l'aire $S$ et en déduire une valeur approchée du volume $V$ de la cuve au m$^3$ près.
Partie B
Pour tout réel $x$ compris entre 2 et 2e, on note $v(x)$ le volume d'eau, exprimé en m$^3$, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est égale à $f(x)$. On admet que, pour tout réel $x$ de l'intervalle [2 ; 2e], \[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]
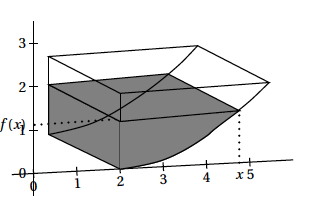
- Quel volume d'eau, au m$^3$ près, y a-t-il dans la cuve lorsque la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que $V$ est le volume total de la cuve, $f$ est la fonction définie en début d'exercice et $v$ la fonction définie dans la partie B.
On considère l'algorithme ci-contre. Interpréter le résultat que cet algorithme permet d'afficher. $$\begin{array}{ |l|c|}\hline \text{Variables} : & a \text{est un réel}\\ & b \text{ est un réel}\\ \text{Traitement :}& a \text{ prend la valeur } 2\\ & b \text{ prend la valeur } 2 e\\ &\text{ Tant que } v(b) - v(a) > 10^{-3} \text{ faire :}\\ &\hspace{0.4cm}\begin{array}{|l} c \text{ prend la valeur } (a+b)/2 \\ \text{Si } v(c) < V/2 , \text{ alors :}\\ \hspace{0.4cm}\begin{array}{|l} a \text{ prend la valeur } c\\ \end{array}\\ \text{ Sinon }\\ \hspace{0.4cm} \begin{array}{|l} b \text{ prend la valeur } c\\ \end{array}\\ \text{Fin Si}\\ \end{array}\\ &\text{Fin Tant que}\\ \text{Sortie :} &\text{Afficher } f(c) \\ \hline \end{array} $$
Correction de l'exercice 2 (6 points)
Un particulier veut faire fabriquer un récupérateur d'eau. Ce récupérateur d'eau est une cuve qui doit respecter le cahier des charges suivant :
Cette cuve est schématisée ci-contre. |

|
La partie incurvée est modélisée par la courbe $\mathcal{C}_f$ de la fonction $f$ sur l'intervalle $[2~;~2 \text{e}]$ définie par: \[f(x) = x\ln \left( \dfrac{x}{2}\right) - x + 2.\] La courbe $\mathcal{C}_f$ est représentée ci-dessous dans un repère orthonormé d'unité 1 m et constitue une vue de profil de la cuve. On considère les points A(2 ; 2), I(2 ; 0) et B(2e ; 2).

Partie A
L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points B et I appartiennent à la courbe $\mathcal{C}_f$ et que l'axe des abscisses est tangent à la courbe $\mathcal{C}_f$ au point I. $\quad$
- On note $\mathcal{T}$ la tangente à la courbe $\mathcal{C}_f$ au point B, et D le point d'intersection de la droite $\mathcal{T}$ avec l'axe des abscisses.
- Déterminer une équation de la droite$\mathcal{T}$ et en déduire les coordonnées de D. Une équation d’une tangente au point d’abscisse $a$ est de la forme $y=f'(a)(x-a)+f(a)$.
- On appelle $S$ l'aire du domaine délimité par la courbe $\mathcal{C}_f$, les droites d'équations $y = 2, x = 2$ et $x = 2\text{e}$. $S$ peut être encadrée par l'aire du triangle ABI et celle du trapèze AIDB. Quel encadrement du volume de la cuve peut-on en déduire ? Aire du triangle $ABI$ : $\mathscr{A}_1 = \dfrac{AB\times AI}{2} = \dfrac{(2\text{e}-2)\times 2}{2}=2\text{e}-2$.
$f'(2\text{e})=\ln(\text{e})=1$.
Ainsi une équation de $\mathscr{T}$ est :
$y=1(x-2\text{e})+2$
soit $y=x-2\text{e}+2$.
Le point $D$ appartient à l’axe des abscisses donc $y_D=0$.
On veut ainsi résoudre $x_D-2\text{e}+2=0$ soit $x_D= 2\text{e}-2$.
Ainsi $D(2\text{e}-2;0)$.
$\quad$
Aire du trapèze $AIDB$ : $\mathscr{A}_2 = \dfrac{(AB+ID)\times AI}{2}=\dfrac{\left(2\text{e}-2+(2\text{e}-2-2)\right)\times 2}{2}=4\text{e}-6$
Ainsi le volume de la cuve est compris $5\times(2\text{e}-2)=10\text{e}-10$ m$^3$ et $5(4\text{e}-6)=20\text{e}-30$ m$^3$.
$\quad$ -
- Montrer que, sur l'intervalle [2 ;2e], la fonction $G$ définie par \[G(x) = \dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - \dfrac{x^2}{4}\] est une primitive de la fonction $g$ définie par $g(x) = x\ln \left( \dfrac{x}{2}\right)$. $G$ est une fonction dérivable sur l’intervalle $[2;2\text{e}]$ en tant que somme de fonctions dérivables sur cet intervalle.
- En déduire une primitive $F$ de la fonction $f$ sur l'intervalle [2 ; 2e]. Une primitive de $f$ sur l’intervalle $[2;2\text{e}]$ est donc définie pour tout $x$ de cet intervalle par :
- Déterminer la valeur exacte de l'aire $S$ et en déduire une valeur approchée du volume $V$ de la cuve au m$^3$ près.
Pour tout réel $x$ de $[2;2\text{e}]$ on a :
$\begin{align*} G'(x)&=x\ln\left(\dfrac{x}{2}\right)+\dfrac{x^2}{2}\times \dfrac{\dfrac{1}{2}}{\dfrac{x}{2}}-\dfrac{x}{2} \\\\
&=x\ln\left(\dfrac{x}{2}\right)+\dfrac{x}{2}-\dfrac{x}{2} \\\\
&=g(x)
\end{align*}$
Donc $G$ est une primitive de $g$ sur l’intervalle $[2;2\text{e}]$.
$\quad$
$\begin{align*} F(x)&=G(x)-\dfrac{x^2}{2}+2x\\
&= \dfrac{x^2}{2}\ln\left(\dfrac{x}{2}\right)-\dfrac{x^2}{4}-\dfrac{x^2}{2}+2x\\
&= \dfrac{x^2}{2}\ln\left(\dfrac{x}{2}\right)-\dfrac{3x^2}{4}+2x
\end{align*}$
$\quad$
$\begin{align*} S&=\displaystyle \int_2^{2\text{e}} \left(2-f(x)\right)\mathrm{d}x \\\\
&=\int_2^{2\text{e}}2\mathrm{d}x-\int_2^{2\text{e}}f(x)\mathrm{d}x \\\\
&=2(2\text{e}-2)-\left(F(2\text{e})-F(2)\right) \\\\
&= 4\text{e}-4-\left(2\text{e}^2\ln(\text{e})-3\text{e}^2+4\text{e}-\left(2\ln(1)-3+4\right)\right) \\\\
&=4\text{e}-4-\left(2\text{e}^2-3\text{e}^2+4\text{e}-1\right) \\\\
&=4\text{e}-4-\left(\text{e}^2+4\text{e}-1\right) \\\\
&=\text{e}^2-3
\end{align*}$
Ainsi $V=5S=5\text{e}^2-15$ m$^3$ $\approx 22$ m$^3$.
$\quad$
$\begin{align*} f(2\text{e})&=2\text{e}\ln\left(\dfrac{2\text{e} }{2}\right)-2\text{e}+2 \\
&=2\text{e}\ln(\text{e})-2\text{e}+2\\
&=2\text{e}-2\text{e}+2\\
&=2
\end{align*}$
Donc $B$ appartient bien à la courbe $\mathscr{C}_f$.
$\quad$
$\begin{align*} f(2)&=2\ln\left(\dfrac{2}{2}\right)-2+2 \\
&=2\ln(1) \\
&=0
\end{align*}$.
Donc $I$ appartient bien également à la courbe $\mathscr{C}_f$.
$\quad$
$\begin{align*} f'(x)&=\ln\left(\dfrac{x}{2}\right)+x\times \dfrac{\dfrac{1}{2}}{\dfrac{x}{2}}-1 \\\\
&=\ln\left(\dfrac{x}{2}\right)+1-1 \\\\
&=\ln\left(\dfrac{x}{2}\right)
\end{align*}$
Ainsi $f'(2)=\ln(1)=0$.
L’axe des abscisses est donc tangent à la courbe $\mathscr{C}_f$ au point $I$.
$\quad$
Partie B
Pour tout réel $x$ compris entre 2 et 2e, on note $v(x)$ le volume d'eau, exprimé en m$^3$, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est égale à $f(x)$. On admet que, pour tout réel $x$ de l'intervalle [2 ; 2e], \[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]

- Quel volume d'eau, au m$^3$ près, y a-t-il dans la cuve lorsque la hauteur d'eau dans la cuve est de un mètre ? On cherche la valeur de $x$ telle que $f(x)=1$
- On rappelle que $V$ est le volume total de la cuve, $f$ est la fonction définie en début d'exercice et $v$ la fonction définie dans la partie B.
On considère l'algorithme ci-contre. Interpréter le résultat que cet algorithme permet d'afficher. $$\begin{array}{ |l|c|}\hline \text{Variables} : & a \text{est un réel}\\ & b \text{ est un réel}\\ \text{Traitement :}& a \text{ prend la valeur } 2\\ & b \text{ prend la valeur } 2 e\\ &\text{ Tant que } v(b) - v(a) > 10^{-3} \text{ faire :}\\ &\hspace{0.4cm}\begin{array}{|l} c \text{ prend la valeur } (a+b)/2 \\ \text{Si } v(c) < V/2 , \text{ alors :}\\ \hspace{0.4cm}\begin{array}{|l} a \text{ prend la valeur } c\\ \end{array}\\ \text{ Sinon }\\ \hspace{0.4cm} \begin{array}{|l} b \text{ prend la valeur } c\\ \end{array}\\ \text{Fin Si}\\ \end{array}\\ &\text{Fin Tant que}\\ \text{Sortie :} &\text{Afficher } f(c) \\ \hline \end{array} $$ Cet algorithme permet d’afficher la hauteur d’eau dans la cuve pour que celle-ci soit remplie à moitié.
La fonction $f$ est continue sur $[2;2\text{e}]$.
$f'(x)=\ln\left(\dfrac{x}{2}\right)$
Pour $x\geqslant 2$ on a $\dfrac{x}{2} \geqslant 1$
Donc sur $[2;2\text{e}]$, $f'(x) \geqslant 0$.
$f$ est donc strictement croissante sur $[2;2\text{e}]$.
$f(2)=0$ et $f(2\text{e})=2$.
$1\in [0;2]$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), il existe un unique réel $\alpha \in [2;2\text{e}]$ tel que $f(\alpha)=1$.
$\alpha \approx 4,311$.
$V(\alpha) \approx 7,453$.
Il y a donc environ $7$ m$^3$ d’eau dans la cuve quand la hauteur d’eau est de un mètre.
$\quad$
Exercice 3 3 points
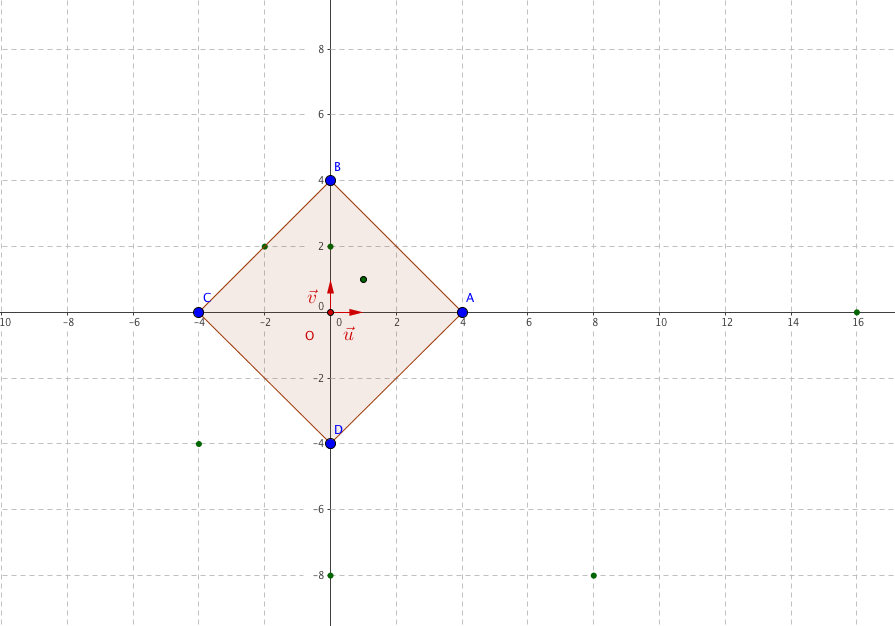
Le plan complexe est rapporté à un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On considère le point A d'affixe 4, le point B d'affixe 4i et les points C et D tels que ABCD est un carré de centre O. Pour tout entier naturel non nul $n$, on appelle $M_n$ le point d'affixe $z_n = (1 + \text{i})^n$.
- Écrire le nombre $1 + \text{i}$ sous forme exponentielle.
- Montrer qu'il existe un entier naturel $n_0$, que l'on précisera, tel que, pour tout entier $n \geqslant n_0$, le point $M_n$ est à l'extérieur du carré ABCD.
Correction de l'exercice 3 (3 points)
Le plan complexe est rapporté à un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On considère le point A d'affixe 4, le point B d'affixe 4i et les points C et D tels que ABCD est un carré de centre O. Pour tout entier naturel non nul $n$, on appelle $M_n$ le point d'affixe $z_n = (1 + \text{i})^n$.
- Écrire le nombre $1 + \text{i}$ sous forme exponentielle. $|1+\text{i}|=\sqrt{2}$
- Montrer qu'il existe un entier naturel $n_0$, que l'on précisera, tel que, pour tout entier $n \geqslant n_0$, le point $M_n$ est à l'extérieur du carré ABCD. La longueur d’une demi diagonale est donc $4$.
Donc $1+\text{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\text{i}\right)=\sqrt{2}\text{e}^{\text{i}\pi/4}$.
$\quad$En vidéo !
Si $OM_n > 4$ alors le point $M_n$ est à l’extérieur du carré $ABCD$.
$\begin{align*} \left|(1+\text{i})^n\right| > 4 &\iff \sqrt{2}^n > 4 \\\\
&\iff n\ln \sqrt{2} > \ln 4 \\\\
&\iff n > \dfrac{\ln 4}{\ln \sqrt{2}} \\\\
&\iff n > \dfrac{2\ln2}{\dfrac{1}{2}\ln 2} \\\\
&\iff n > 4
\end{align*}$
Ainsi si $n>4$ alors le point $M_n$ est à l’extérieur du carré $ABCD$. Donc $n_0=5$ convient.
Exercice 4 5 points
On considère la pyramide régulière SABCD de sommet S constituée de la base carrée ABCD et de triangles équilatéraux représentée ci-dessous.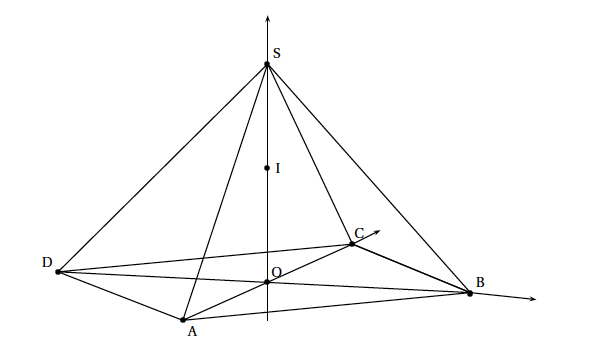
Le point O est le centre de la base ABCD avec OB $= 1$. On rappelle que le segment [SO] est la hauteur de la pyramide et que toutes les arêtes ont la même longueur.
- Justifier que le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$ est orthonormé. Dans la suite de l'exercice, on se place dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$.
- On définit le point K par la relation $\vec{\text{SK}} = \dfrac{1}{3} \vec{\text{SD}}$ et on note I le milieu du segment [SO].
- Déterminer les coordonnées du point K.
- En déduire que les points B, I et K sont alignés.
- On note L le point d'intersection de l'arête [SA] avec le plan (BCI). Justifier que les droites (AD) et (KL) sont parallèles.
- Déterminer les coordonnées du point L.
- On considère le vecteur $\vec{n}\begin{pmatrix}1\\1\\2\end{pmatrix}$ dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$.
- Montrer que $\vec{n}$ est un vecteur normal au plan (BCI).
- Montrer que les vecteurs $\vec{n},\: \vec{\text{AS}}$ et $\vec{\text{DS}}$ sont coplanaires.
- Quelle est la position relative des plans (BCI) et (SAD) ?
Correction de l'exercice 4 5 points
On considère la pyramide régulière SABCD de sommet S constituée de la base carrée ABCD et de triangles équilatéraux représentée ci-dessous.
Le point O est le centre de la base ABCD avec OB $= 1$. On rappelle que le segment [SO] est la hauteur de la pyramide et que toutes les arêtes ont la même longueur.
- Justifier que le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$ est orthonormé. Dans la suite de l'exercice, on se place dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$. $ABCD$ est un carré de centre $O$ tel que $OB=1$.
- On définit le point K par la relation $\vec{\text{SK}} = \dfrac{1}{3} \vec{\text{SD}}$ et on note I le milieu du segment [SO].
- Déterminer les coordonnées du point K. $\vec{OD}=-\vec{OB}$. Donc les coordonnées de $D$ sont $(-1;0;0)$. On a de plus $S(0;0;1)$
- En déduire que les points B, I et K sont alignés. $I(0;0;0,5)$ et $B(1;0;0)$
- On note L le point d'intersection de l'arête [SA] avec le plan (BCI). Justifier que les droites (AD) et (KL) sont parallèles. On appelle $L’$ le point défini par la relation $\vec{SL’}=\dfrac{1}{3}\vec{SA}$.
- Déterminer les coordonnées du point L. $A(0;-1;0)$ et $D(-1;0;0)$ donc $\vec{AD}(-1;1;0)$.
Ainsi $\vec{SD}(-1;0;-1)$.
Par conséquent :
$\begin{align*} \vec{SK}=\dfrac{1}{3}\vec{SD} &\iff \begin{cases} x_K = \dfrac{1}{3}\times (-1) \\y_K=\dfrac{1}{3}\times 0 \\z_K-1=\dfrac{1}{3}\times (-1) \end{cases} \\
&\iff \begin{cases} x_k=-\dfrac{1}{3} \\y_k=0 \\z_k=1-\dfrac{1}{3} \end{cases} \\
&\iff K\left(-\dfrac{1}{3};0;\dfrac{2}{3}\right)
\end{align*}$
$\quad$
Ainsi $\vec{BI}(-1;0;0,5)$
$\vec{BK}\left(-\dfrac{4}{3};0;\dfrac{2}{3}\right)$
Ainsi $\vec{BK}=\dfrac{4}{3}\vec{BI}$.
Les vecteurs sont donc colinéaires et les points $B$, $I$ et $K$ sont alignés.
$\quad$
Pour les mêmes raisons qu’à la question précédente $C$, $I$ et $L’$ sont alignés.
Ainsi $L’$ est l’intersection de $(CI)$ et de $(SA)$.
Donc $L=L’$.
Par conséquent :
$\begin{align*} \vec{LK}&=\vec{LS}+\vec{SK} \\
&=\dfrac{1}{3}\vec{AS}+\dfrac{1}{3}\vec{SD} \\
&=\dfrac{1}{3}\left(\vec{AS}+\vec{SD}\right) \\
&=\dfrac{1}{3}\vec{AD}
\end{align*}$
Les droites $(AD)$ et $(KL)$ sont donc parallèles.
$\quad$
Par conséquent :
$\begin{align*} \vec{LK}=\dfrac{1}{3}\vec{AD} &\iff \begin{cases} -\dfrac{1}{3}-x_L = \dfrac{-1}{3} \\0-y_L=\dfrac{1}{3} \\ \dfrac{2}{3}-z_L=0 \end{cases} \\
&\iff \begin{cases} x_L=0 \\ y_L=-\dfrac{1}{3}\\z_L=\dfrac{2}{3}\end{cases} \end{align*}$
$\quad$ - On considère le vecteur $\vec{n}\begin{pmatrix}1\\1\\2\end{pmatrix}$ dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$.
- Montrer que $\vec{n}$ est un vecteur normal au plan (BCI). $\vec{BC}(-1;1;0)$ donc $\vec{BC}.\vec{n}=-1+1+0=0$.
- Montrer que les vecteurs $\vec{n},\: \vec{\text{AS}}$ et $\vec{\text{DS}}$ sont coplanaires. On a $\vec{AS} \begin{pmatrix}0\\1\\1\end{pmatrix}$ et $\vec{DS} \begin{pmatrix}1\\0\\1\end{pmatrix}$
- Quelle est la position relative des plans (BCI) et (SAD) ? Il existe donc une droite de $(SAD)$ dont un vecteur directeur est $\vec{n}$.
$\vec{BI}(-1;0;0,5)$ donc $\vec{BI}.\vec{n}=-1+0+1=0$.
Les deux vecteurs $\vec{BI}$ et $\vec{BC}$ ne sont clairement pas colinéaires.
Le vecteurs $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(BCI)$. Il est par conséquent normal à ce plan.
$\quad$
Donc $\vec{n}=\vec{AS}+\vec{DS}$.
Ces trois vecteurs sont par conséquent coplanaires.
$\quad$
Cette droite est par conséquent perpendiculaire au plan $(BCI)$.
Les plans $(SAD)$ et $(BCI)$ sont donc perpendiculaires.
Ainsi $OB=OC=1$.
Les diagonales d’un carré sont perpendiculaires donc $\vec{OB}.\vec{OC}=0$.
$[OS]$ est la hauteur de la pyramide donc $(OS)$ est perpendiculaire au plan $(OBC)$. Ainsi $\vec{OS}$ est orthogonal à $\vec{OB}$ et $\vec{OC}$.
Il ne reste plus qu’à montrer que $OS=1$.
Dans le triangle $OBC$ rectangle en $O$ on applique le théorème de Pythagore.
Ainsi $BC^2=OB^2+OC^2=2$ donc $BC=\sqrt{2}$.
Toutes les arrêtes ayant la même longueur, on a également $AS=\sqrt{2}$.
Dans le triangle $OAS$ rectangle en $O$ on applique le théorème de Pythagore :
$\begin{align*} AS^2=OS^2+OA^2&\iff 2=OS^2+1 \\
&\iff 1=OS^2 \\
&\iff OS=1
\end{align*}$
Le repère $\left(O;\vec{OB},\vec{OC},\vec{OS}\right)$ est donc orthonormé.
$\quad$
Spécialité 5 points
On dispose de deux urnes U et V contenant chacune deux boules. Au départ, l'urne U contient deux boules blanches et l'urne V contient deux boules noires. On effectue des tirages successifs dans ces urnes de la façon suivante : chaque tirage consiste à prendre au hasard, de manière simultanée, une boule dans chaque urne et à la mettre dans l'autre urne. Pour tout entier naturel $n$ non nul, on note $X_n$ la variable aléatoire égale au nombre de boules blanches que contient l'urne U à la fin du $n$-ième tirage.
-
- Traduire par une phrase la probabilité $P_{(X_n=1)} \left(X_{n+1} = 1\right)$ puis déterminer les probabilités conditionnelles suivantes : \[P_{(X_n=0)} \left(X_{n+1} = 1\right) , P_{(X_n=1)} \left(X_{n+1} = 1\right)\:\: \text{et}\:\: P_{(X_n=2)} \left(X_{n+1} = 1\right).\]
- Exprimer $P\left(X_{n+1} = 1\right)$ en fonction de $P\left(X_n = 0\right),\: P\left(X_n = 1\right)$ et $P\left(X_n = 2\right)$.
- Pour tout entier naturel $n$ non nul, on note $R_n$ la matrice ligne définie par : \[R_n = \begin{pmatrix}P\left(X_n = 0\right)& P\left(X_n = 1\right)& P\left(X_n = 2\right)\end{pmatrix}\] et on considère $M$ la matrice $\begin{pmatrix}0&1&0\\\dfrac{1}{4}&\dfrac{1}{2}&\dfrac{1}{4}\\0&1&0\end{pmatrix}$. On note $R_0$ la matrice ligne $\begin{pmatrix}0 &0 &1\end{pmatrix}$. On admettra par la suite que, pour tout entier naturel $n,\: R_{n+1} = R_n \times M$. Déterminer $R_1$ et justifier que, pour tout entier naturel $n,\: R_n = R_0 \times M^n$.
- On admet que $M = P \times D \times P^{- 1}$ avec : \[P = \dfrac{1}{6} \begin{pmatrix}2&3&1\\- 1&0&1\\2&- 3&1\end{pmatrix}, \: \: D = \begin{pmatrix}- \dfrac{1}{2}&0&0\\0&0&0\\0&0&1\end{pmatrix}\:\:\text{et}\:\: P^{-1} = \begin{pmatrix}1&-2&1\\1&0&- 1\\1&4&1\end{pmatrix}.\] Établir que, pour tout entier naturel $n,\: M^n = P \times D^n \times P^{-1}$.
On admettra que, pour tout entier naturel $n,\: D^n = \begin{pmatrix} \left(- \dfrac{1}{2} \right)^n&0&0\\0&0&0\\0&0&1\end{pmatrix}$. -
- Calculer $D^n \times P^{-1}$ en fonction de $n$.
- Sachant que $R_0P = \begin{pmatrix}\dfrac{1}{3}&- \dfrac{1}{2}&\dfrac{1}{6} \end{pmatrix}$, déterminer les coefficients de $R_n$ en fonction de $n$.
- Déterminer $\displaystyle\lim_{n \to + \infty} P\left(X_n = 0\right),\: \displaystyle\lim_{n \to + \infty} P\left(X_n = 1\right)$ et $\displaystyle\lim_{n \to + \infty} P\left(X_n = 2\right)$. Interpréter ces résultats.
Correction de l'exercice de Spécialité 5 points
On dispose de deux urnes U et V contenant chacune deux boules. Au départ, l'urne U contient deux boules blanches et l'urne V contient deux boules noires. On effectue des tirages successifs dans ces urnes de la façon suivante : chaque tirage consiste à prendre au hasard, de manière simultanée, une boule dans chaque urne et à la mettre dans l'autre urne. Pour tout entier naturel $n$ non nul, on note $X_n$ la variable aléatoire égale au nombre de boules blanches que contient l'urne U à la fin du $n$-ième tirage.
-
- Traduire par une phrase la probabilité $P_{(X_n=1)} \left(X_{n+1} = 1\right)$ puis déterminer les probabilités conditionnelles suivantes : \[P_{(X_n=0)} \left(X_{n+1} = 1\right) , P_{(X_n=1)} \left(X_{n+1} = 1\right)\:\: \text{et}\:\: P_{(X_n=2)} \left(X_{n+1} = 1\right).\] $P_{\left\{X_n=0\right\}}\left(X_{n+1}=1\right)$ correspond à la probabilité que l’urne $U$ contiennent une boule blanche au $n+1$-ième tirage sachant qu’elle n’en contenait pas au $n$-ième tirage.
- Exprimer $P\left(X_{n+1} = 1\right)$ en fonction de $P\left(X_n = 0\right),\: P\left(X_n = 1\right)$ et $P\left(X_n = 2\right)$. D’après la formule des probabilités totales on a :
S’il n’y a pas de boule blanche au $n$-ième tirage dans l’urne $U$ alors on est certain d’en avoir une au tirage suivant (à chaque tirage les deux urnes contiennent exactement deux boules)
Donc $P_{\left\{X_n=0\right\}}\left(X_{n+1}=1\right)=1$.
De la même manière si l’urne $U$ contient deux boules blanches au $n$-ième tirage alors elle contiendra exactement une boule blanche au tirage suivant.
Ainsi $P_{\left\{X_n=2\right\}}\left(X_{n+1}=1\right)=1$.
Si l’urne $U$ contient une boule blanche au $n$-ième tirage alors quatre possibilités équiprobables se présentent :
– on tire la boule blanche de $U$ et la boule noire de $V$ : $\left(X_{n+1}=0\right)$
– on tire la boule blanche de $U$ et la boule blanche de $V$ : $\left(X_{n+1}=1\right)$
– on tire la boule noire de $U$ et la boule blanche de $V$ : $\left(X_{n+1}=2\right)$
– on tire la boule noire de $U$ et la boule noire de $V$ : $\left(X_{n+1}=1\right)$
Ainsi $P_{\left\{X_n=1\right\}}\left(X_{n+1}=1\right)=\dfrac{2}{4}=\dfrac{1}{2}$.
$\quad$
$\begin{align*} P\left(X_{n+1}=1\right) & = P\left(\left\{X_{n+1}=1\right\}\cap \left\{X_n=0\right\}\right)+P\left(\left\{X_{n+1}=1\right\}\cap \left\{X_n=1\right\}\right)+P\left(\left\{X_{n+1}=1\right\}\cap \left\{X_n=2\right\}\right) \\
&= P\left(X_n=0\right) \times P_{\left\{X_n=0\right\}}\left(X_{n+1}=1\right)\\
&\phantom{= }+P\left(X_n=1\right) \times P_{\left\{X_n=1\right\}}\left(X_{n+1}=1\right) \\
&\phantom{= }+P\left(X_n=2\right) \times P_{\left\{X_n=2\right\}}\left(X_{n+1}=1\right) \\
&=P\left(X_n=0\right)+\dfrac{1}{2}P\left(X_n=1\right) +P\left(X_n=2\right)\end{align*}$ - Pour tout entier naturel $n$ non nul, on note $R_n$ la matrice ligne définie par : \[R_n = \begin{pmatrix}P\left(X_n = 0\right)& P\left(X_n = 1\right)& P\left(X_n = 2\right)\end{pmatrix}\] et on considère $M$ la matrice $\begin{pmatrix}0&1&0\\\dfrac{1}{4}&\dfrac{1}{2}&\dfrac{1}{4}\\0&1&0\end{pmatrix}$. On note $R_0$ la matrice ligne $\begin{pmatrix}0 &0 &1\end{pmatrix}$. On admettra par la suite que, pour tout entier naturel $n,\: R_{n+1} = R_n \times M$. Déterminer $R_1$ et justifier que, pour tout entier naturel $n,\: R_n = R_0 \times M^n$. $R_1=R_0\times M = \begin{pmatrix}0&1&0\end{pmatrix}$
- On admet que $M = P \times D \times P^{- 1}$ avec : \[P = \dfrac{1}{6} \begin{pmatrix}2&3&1\\- 1&0&1\\2&- 3&1\end{pmatrix}, \: \: D = \begin{pmatrix}- \dfrac{1}{2}&0&0\\0&0&0\\0&0&1\end{pmatrix}\:\:\text{et}\:\: P^{-1} = \begin{pmatrix}1&-2&1\\1&0&- 1\\1&4&1\end{pmatrix}.\] Établir que, pour tout entier naturel $n,\: M^n = P \times D^n \times P^{-1}$.
On admettra que, pour tout entier naturel $n,\: D^n = \begin{pmatrix} \left(- \dfrac{1}{2} \right)^n&0&0\\0&0&0\\0&0&1\end{pmatrix}$. -
- Calculer $D^n \times P^{-1}$ en fonction de $n$. On montre par récurrence que, pour tout entier naturel $n$ on a $M^n=P\times D^n\times P^{-1}$.
- Sachant que $R_0P = \begin{pmatrix}\dfrac{1}{3}&- \dfrac{1}{2}&\dfrac{1}{6} \end{pmatrix}$, déterminer les coefficients de $R_n$ en fonction de $n$.
Initialisation : Si $n=0$ alors $P\times D^0\times P^{-1}= P\times P^{-1}=I_3$
Et $M^0=I_3$
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $M^n=P\times D^n\times P^{-1}$
$M_{n+1}=M\times M^n =P\times D\times P^{-1} \times P\times D_n\times P^{-1} = P\times D^{n+1}\times P^{-1}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Donc pour tout entier naturel $n$ on a $M^n=P\times D^n\times P^{-1}$.
$\quad$ $D^n\times P^{-1}=\begin{pmatrix} \left(-\dfrac{1}{2}\right)^n&-2\left(-\dfrac{1}{2}\right)^n&\left(-\dfrac{1}{2}\right)^n\\ - Déterminer $\displaystyle\lim_{n \to + \infty} P\left(X_n = 0\right),\: \displaystyle\lim_{n \to + \infty} P\left(X_n = 1\right)$ et $\displaystyle\lim_{n \to + \infty} P\left(X_n = 2\right)$. Interpréter ces résultats. Puisque $-1<-\dfrac{1}{2}<1$ alors $\lim\limits_{n\to +\infty} \left(-\dfrac{1}{2}\right)^n = 0$.
$\quad$
Montrons par récurrence que $R_n=R_0\times M^n$.
Initialisation : Si $n=0$ alors $R_0 \times M^0=R_0 \times I_3 = R_0$ où $I_3$ est la matrice identité d’ordre $3$.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $R_n=R_0\times M^n$.
Alors $R_{n+1}=R_n \times M = R_0\times M^n \times M = R_0\times M^{n+1}$.
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Donc pour tout entier naturel $n$ on a $R_n=R_0\times M^n$.
$\quad$
0&0&0 \\
1&4&1\end{pmatrix}$
$\quad$
b. On a donc $R_n=R_0P\times D^n\times P^{-1}$
D’où $R_n=\begin{pmatrix}\dfrac{\left(-\dfrac{1}{2}\right)^n}{3}+\dfrac{1}{6}&-\dfrac{2\left(-\dfrac{1}{2}\right)^n}{3}+\dfrac{2}{3}&\dfrac{\left(-\dfrac{1}{2}\right)^n}{3}+\dfrac{1}{6}\end{pmatrix}$.
$\quad$
Ainsi :
$\lim\limits_{n \to +\infty} P\left(X_n=0\right) = \dfrac{1}{6}$
$\lim\limits_{n \to +\infty} P\left(X_n=1\right) = \dfrac{2}{3}$
$\lim\limits_{n \to +\infty} P\left(X_n=2\right) = \dfrac{1}{6}$
Or pour $n \in\mathbb N$ $R_n$ est la matrice ligne définie par : $R_n =\begin{pmatrix} P (X_n = 0) &P (X_n = 1)& P (X_n = 2) \end{pmatrix}$
Cela signifie donc qu'après un très grand nombre de tirages, la probabilité d'avoir une boule blanche dans l'urne U est de $\dfrac{2}{3}$, d'en avoir aucune $\dfrac{1}{6}$ et d'en avoir deux de $\dfrac{1}{6}$.
- Vues: 19245
