Baccalauréat S Amérique du Nord 1er juin 2016 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

Un particulier veut faire fabriquer un récupérateur d'eau. Ce récupérateur d'eau est une cuve qui doit respecter le cahier des charges suivant :

elle doit être située à deux mètres de sa maison; la profondeur maximale doit être de deux mètres; elle doit mesurer cinq mètres de long; elle doit épouser la pente naturelle du terrain. Cette cuve est schématisée ci-contre.

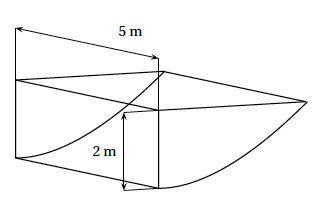
La partie incurvée est modélisée par la courbe $\mathcal{C}_f$ de la fonction $f$ sur l'intervalle $[2~;~2 \text{e}]$ définie par: \[f(x) = x\ln \left( \dfrac{x}{2}\right) - x + 2.\] La courbe $\mathcal{C}_f$ est représentée ci-dessous dans un repère orthonormé d'unité 1 m et constitue une vue de profil de la cuve. On considère les points A(2 ; 2), I(2 ; 0) et B(2e ; 2).

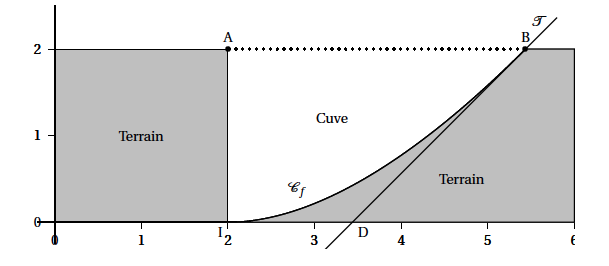
Partie A

L'objectif de cette partie est d'évaluer le volume de la cuve.

1. Justifier que les points B et I appartiennent à la courbe $\mathcal{C}_f$ et que l'axe des abscisses est tangent à la courbe $\mathcal{C}_f$ au point I.
$\quad$
$\begin{align*} f(2\text{e})&=2\text{e}\ln\left(\dfrac{2\text{e} }{2}\right)-2\text{e}+2 \\
&=2\text{e}\ln(\text{e})-2\text{e}+2\\
&=2\text{e}-2\text{e}+2\\
&=2
\end{align*}$
Donc $B$ appartient bien à la courbe $\mathscr{C}_f$.
$\quad$
$\begin{align*} f(2)&=2\ln\left(\dfrac{2}{2}\right)-2+2 \\
&=2\ln(1) \\
&=0
\end{align*}$.
Donc $I$ appartient bien également à la courbe $\mathscr{C}_f$.
$\quad$
$\begin{align*} f'(x)&=\ln\left(\dfrac{x}{2}\right)+x\times \dfrac{\dfrac{1}{2}}{\dfrac{x}{2}}-1 \\\\
&=\ln\left(\dfrac{x}{2}\right)+1-1 \\\\
&=\ln\left(\dfrac{x}{2}\right)
\end{align*}$
Ainsi $f'(2)=\ln(1)=0$.
L’axe des abscisses est donc tangent à la courbe $\mathscr{C}_f$ au point $I$.
$\quad$
2. On note $\mathcal{T}$ la tangente à la courbe $\mathcal{C}_f$ au point B, et D le point d'intersection de la droite $\mathcal{T}$ avec l'axe des abscisses.
   1. Déterminer une équation de la droite$\mathcal{T}$ et en déduire les coordonnées de D.
   Une équation d’une tangente au point d’abscisse $a$ est de la forme $y=f'(a)(x-a)+f(a)$.
   $f'(2\text{e})=\ln(\text{e})=1$.
   Ainsi une équation de $\mathscr{T}$ est :
   $y=1(x-2\text{e})+2$
   soit $y=x-2\text{e}+2$.
   Le point $D$ appartient à l’axe des abscisses donc $y_D=0$.
   On veut ainsi résoudre $x_D-2\text{e}+2=0$ soit $x_D= 2\text{e}-2$.
   Ainsi $D(2\text{e}-2;0)$.
   $\quad$
   
   2. On appelle $S$ l'aire du domaine délimité par la courbe $\mathcal{C}_f$, les droites d'équations $y = 2, x = 2$ et $x = 2\text{e}$. $S$ peut être encadrée par l'aire du triangle ABI et celle du trapèze AIDB. Quel encadrement du volume de la cuve peut-on en déduire ?
   Aire du triangle $ABI$ : $\mathscr{A}_1 = \dfrac{AB\times AI}{2} = \dfrac{(2\text{e}-2)\times 2}{2}=2\text{e}-2$.
   Aire du trapèze $AIDB$ : $\mathscr{A}_2 = \dfrac{(AB+ID)\times AI}{2}=\dfrac{\left(2\text{e}-2+(2\text{e}-2-2)\right)\times 2}{2}=4\text{e}-6$
   Ainsi le volume de la cuve est compris $5\times(2\text{e}-2)=10\text{e}-10$ m$^3$ et $5(4\text{e}-6)=20\text{e}-30$ m$^3$.
   $\quad$
3. 1. Montrer que, sur l'intervalle [2 ;2e], la fonction $G$ définie par \[G(x) = \dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - \dfrac{x^2}{4}\] est une primitive de la fonction $g$ définie par $g(x) = x\ln \left( \dfrac{x}{2}\right)$.
   $G$ est une fonction dérivable sur l’intervalle $[2;2\text{e}]$ en tant que somme de fonctions dérivables sur cet intervalle.
   Pour tout réel $x$ de $[2;2\text{e}]$ on a :
   $\begin{align*} G'(x)&=x\ln\left(\dfrac{x}{2}\right)+\dfrac{x^2}{2}\times \dfrac{\dfrac{1}{2}}{\dfrac{x}{2}}-\dfrac{x}{2} \\\\
   &=x\ln\left(\dfrac{x}{2}\right)+\dfrac{x}{2}-\dfrac{x}{2} \\\\
   &=g(x)
   \end{align*}$
   Donc $G$ est une primitive de $g$ sur l’intervalle $[2;2\text{e}]$.
   $\quad$
   
   2. En déduire une primitive $F$ de la fonction $f$ sur l'intervalle [2 ; 2e].
   Une primitive de $f$ sur l’intervalle $[2;2\text{e}]$ est donc définie pour tout $x$ de cet intervalle par :
   $\begin{align*} F(x)&=G(x)-\dfrac{x^2}{2}+2x\\
   &= \dfrac{x^2}{2}\ln\left(\dfrac{x}{2}\right)-\dfrac{x^2}{4}-\dfrac{x^2}{2}+2x\\
   &= \dfrac{x^2}{2}\ln\left(\dfrac{x}{2}\right)-\dfrac{3x^2}{4}+2x
   \end{align*}$
   $\quad$
   
   3. Déterminer la valeur exacte de l'aire $S$ et en déduire une valeur approchée du volume $V$ de la cuve au m$^3$ près.
   
   $\begin{align*} S&=\displaystyle \int_2^{2\text{e}} \left(2-f(x)\right)\mathrm{d}x \\\\
   &=\int_2^{2\text{e}}2\mathrm{d}x-\int_2^{2\text{e}}f(x)\mathrm{d}x \\\\
   &=2(2\text{e}-2)-\left(F(2\text{e})-F(2)\right) \\\\
   &= 4\text{e}-4-\left(2\text{e}^2\ln(\text{e})-3\text{e}^2+4\text{e}-\left(2\ln(1)-3+4\right)\right) \\\\
   &=4\text{e}-4-\left(2\text{e}^2-3\text{e}^2+4\text{e}-1\right) \\\\
   &=4\text{e}-4-\left(\text{e}^2+4\text{e}-1\right) \\\\
   &=\text{e}^2-3
   \end{align*}$
   Ainsi $V=5S=5\text{e}^2-15$ m$^3$ $\approx 22$ m$^3$.
   $\quad$

 

Partie B

Pour tout réel $x$ compris entre 2 et 2e, on note $v(x)$ le volume d'eau, exprimé en m$^3$, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est égale à $f(x)$. On admet que, pour tout réel $x$ de l'intervalle [2 ; 2e], \[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]
 

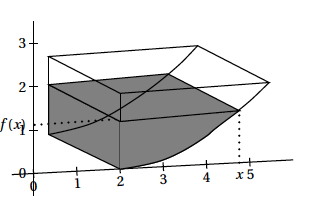
1. Quel volume d'eau, au m$^3$ près, y a-t-il dans la cuve lorsque la hauteur d'eau dans la cuve est de un mètre ?
On cherche la valeur de $x$ telle que $f(x)=1$
La fonction $f$ est continue sur $[2;2\text{e}]$.
$f'(x)=\ln\left(\dfrac{x}{2}\right)$
Pour $x\geqslant 2$ on a $\dfrac{x}{2} \geqslant 1$
Donc sur $[2;2\text{e}]$, $f'(x) \geqslant 0$.
$f$ est donc strictement croissante sur $[2;2\text{e}]$.
$f(2)=0$ et $f(2\text{e})=2$.
$1\in [0;2]$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), il existe un unique réel $\alpha \in [2;2\text{e}]$ tel que $f(\alpha)=1$.
$\alpha \approx 4,311$.
$V(\alpha) \approx 7,453$.
Il y a donc environ $7$ m$^3$ d’eau dans la cuve quand la hauteur d’eau est de un mètre.
$\quad$

2. On rappelle que $V$ est le volume total de la cuve, $f$ est la fonction définie en début d'exercice et $v$ la fonction définie dans la partie B.
   On considère l'algorithme ci-contre. Interpréter le résultat que cet algorithme permet d'afficher. $$\begin{array}{ |l|c|}\hline \text{Variables} : & a \text{est un réel}\\ & b \text{ est un réel}\\ \text{Traitement :}& a \text{ prend la valeur } 2\\ & b \text{ prend la valeur } 2 e\\ &\text{ Tant que } v(b) - v(a) > 10^{-3} \text{ faire :}\\ &\hspace{0.4cm}\begin{array}{|l} c \text{ prend la valeur } (a+b)/2 \\ \text{Si } v(c) < V/2 , \text{ alors :}\\ \hspace{0.4cm}\begin{array}{|l} a \text{ prend la valeur } c\\ \end{array}\\ \text{ Sinon }\\ \hspace{0.4cm} \begin{array}{|l} b \text{ prend la valeur } c\\ \end{array}\\ \text{Fin Si}\\ \end{array}\\ &\text{Fin Tant que}\\ \text{Sortie :} &\text{Afficher } f(c) \\ \hline \end{array} $$
Cet algorithme permet d’afficher la hauteur d’eau dans la cuve pour que celle-ci soit remplie à moitié.