BAC S 2016 de Mathématiques : Polynésie 10 juin 2016 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (7 points)

Commun à tous les candidats

 

Partie A

Voici deux courbes $\mathcal{C}_1$ et $\mathcal{C}_2$ qui donnent pour deux personnes $P_1$ et $P_2$ de corpulences différentes la concentration $C$ d'alcool dans le sang (taux d'alcoolémie) en fonction du temps $t$ après ingestion de la même quantité d'alcool. L'instant $t = 0$ correspond au moment où les deux individus ingèrent l'alcool. $C$ est exprimée en gramme par litre et $t$ en heure.
Définition : La corpulence est le nom scientifique correspondant au volume du corps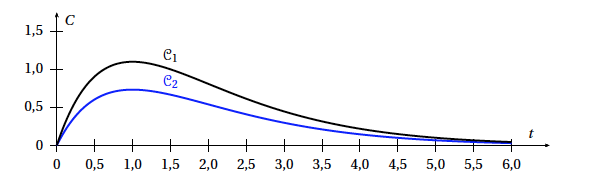

1. La fonction $C$ est définie sur l'intervalle $[0~;~+\infty[$ et on note $C'$ sa fonction dérivée. À un instant $t$ positif ou nul, la vitesse d'apparition d'alcool dans le sang est donnée par $C'(t)$. À quel instant cette vitesse est-elle maximale ?
   On dit souvent qu'une personne de faible corpulence subit plus vite les effets de l'alcool.
La vitesse est maximale quand le coefficient directeur de la tangente en un point de la courbe $C$ est le plus grand. C’est donc pour $t=0$ que cette vitesse est maximale.
$\quad$
2. Sur le graphique précédent, identifier la courbe correspondant à la personne la plus corpulente. Justifier le choix effectué.
Plus la personne est corpulente moins, à quantité d’alcool ingérée égale, la concentration d’alcool dans le sang est importante. La courbe $\mathcal{C}_2$ correspond donc à la personne la plus corpulente.
$\quad$
3. Une personne à jeûn absorbe de l'alcool. On admet que la concentration $C$ d'alcool dans son sang peut être modélisée par la fonction $f$ définie sur $[0~;~+\infty[$ par \[f(t) = A t\text{e}^{-t}\] où $A$ est une constante positive qui dépend de la corpulence et de la quantité d'alcool absorbée.
   1. On note $f'$ la fonction dérivée de la fonction $f$. Déterminer $f'(0)$.
   $f$ est dérivable sur $[0;+\infty[$ en tant que produit de fonctions dérivables sur cet intervalle.
   $f'(t)=A\text{e}^{-t}-At\text{e}^{-t}$
   Donc $f'(0)=A$
   
   2. L'affirmation suivante est-elle vraie ? « À quantité d'alcool absorbée égale, plus $A$ est grand, plus la personne est corpulente. »
   Si on appelle $f_1$ et $f_2$ les fonctions associées aux graphiques $\mathcal{C}_1$ et $\mathcal{C}_2$, on constate que $f’_1(0)>f’_2(0)$.
   Donc $A_1>A_2$ (où $A_i$ est la constante liée à la fonction $f_i$).
   Puisque la courbe $\mathcal{C}_2$ correspond à la personne ayant la forte corpulence, l’affirmation est fausse.
   $\quad$

 

Partie B - Un cas particulier

Paul, étudiant de 19 ans de corpulence moyenne et jeune conducteur, boit deux verres de rhum. La concentration $C$ d'alcool dans son sang est modélisée en fonction du temps $t$, exprimé en heure, par la fonction $f$ définie sur $[0~;~+\infty[$ par \[f(t) = 2 t\text{e}^{-t}.\]

1. Étudier les variations de la fonction $f$ sur l'intervalle $[0~;~+\infty[$.
D’après la question A.3. on a :
$f'(t)=2\text{e}^{-t}-2t\text{e}^{-t}=2\text{e}^{-t}(1-t)$.
La fonction exponentielle est strictement positive.
Le signe de $f'(t)$ ne dépend donc que de $(1-t)$.
Or $1-t>0 \iff t<1$.
Donc $f$ est strictement croissante sur $[0;1]$ et strictement décroissante sur $[1;+\infty[$.
$\quad$
2. À quel instant la concentration d'alcool dans le sang de Paul est-elle maximale ? Quelle est alors sa valeur? Arrondir à $10^{-2}$ près.
La concentration d’alcool dans le sang est donc maximale quand $t=1$.
Et $f(1)=2\text{e}^{-1}\approx 0,74$ g.L$^{-1}$.
$\quad$
3. Rappeler la limite de $\dfrac{\text{e}^t}{t}$ lorsque $t$ tend vers $+ \infty$ et en déduire celle de $f(t)$ en $+ \infty$. Interpréter le résultat dans le contexte de l'exercice.
On a $\lim\limits_{t\to +\infty} \dfrac{\text{e}^t}{t}=+\infty$.
Or $f(t)=2\dfrac{t}{\text{e}^t}=2\dfrac{1}{\dfrac{\text{e}^t}{t}}$.
Donc $\lim\limits_{t \to +\infty} f(t)=0$.
Cela signifie qu’au bout d’un très grand nombre d’heures la concentration d’alcool dans le sang est nulle et donc que l’alcool a disparu de l’organisme.
$\quad$
4. Paul veut savoir au bout de combien de temps il peut prendre sa voiture. On rappelle que la législation autorise une concentration maximale d'alcool dans le sang de $0,2$ g.L$^{-1}$ pour un jeune conducteur.
   1. Démontrer qu'il existe deux nombres réels $t_1$ et $t_2$ tels que $f\left(t_1\right) = f\left(t_2\right) = 0,2$.
   La fonction $f$ est continue (car dérivable) et strictement croissante sur $[0;1]$.
   $f(0)=0<0,2$ et $f(1) \approx 0,74>0,2$
   D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(t)=0,2$ possède une unique solution $t_1$ sur $[0;1]$.
   $\quad$
   On procède de même sur $[1;+\infty[$.
   La fonction $f$ est continue (car dérivable) et strictement croissante sur $[1;+\infty[$.
   $f(1) \approx 0,74>0,2$ et $\lim\limits_{t \to +\infty} f(t)=0<0,2$
   D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(t)=0,2$ possède une unique solution $t_2$ sur $[1;+\infty[$.
   $\quad$
   Il existe donc deux réels $t_1$ et $t_2$ tels que $f(t)=0,2$.
   $\quad$
   
   2. Quelle durée minimale Paul doit-il attendre avant de pouvoir prendre le volant en toute légalité ? Donner le résultat arrondi à la minute la plus proche.
   Sur $\left[t_1;t_2\right]$ $f(t)>0,2$ car $f$ est croissante sur $\left[t_1;1\right]$.
   Donc Paul ne pourra prendre le volant qu’après $t_2$.
   On obtient à l’aide de la calculatrice $t_2\approx 3,577$
   Il faut donc que Paul attendent $3$ heures et $35$ minutes avant de pouvoir reprendre le volant.
   $\quad$
5. La concentration minimale d'alcool détectable dans le sang est estimée à $5 \times 10^{-3}$ g.L$^{-1}$.
   1. Justifier qu'il existe un instant $T$ à partir duquel la concentration d'alcool dans le sang n'est plus détectable.
   Puisque $\lim\limits_{t \to +\infty} f(t)=0$, pour tout réel $\lambda>0$, il existe un temps $T>0$ tel que, pour tout $t>T$ on a $f(t)<\lambda$.
   C’est en particulier vrai pour $\lambda =5\times 10^{-3}$ g.L$^{-1}$.
   Il existe donc un instant $T$ à partir duquel la concentration d’alcool dans le sang n’est plus détectable.
   $\quad$
   
   2. On donne l'algorithme suivant où $f$ est la fonction définie par $f(t) = 2 t\text{e}^{-t}$. $$ \begin{array}{|l |l|}\hline \text{Initialisation} : & t \text{ prend la valeur } 3,5 \\ & p \text{ prend la valeur} 0,25 \\ & C \text{ prend la valeur } 0,21 \\ \text{Traitement} : & \text{Tant que } C > 5 \times 10^{-3} \text{ faire :}\\ &\hspace{0,5cm}\begin{array}{|l} t \text{ prend la valeur } t + p \\ C \text{ prend la valeur } f(t) \end{array}\\ &\text{ Fin Tant que }\\ \text{Sortie}: &\text{ Afficher } t \\ \hline \end{array}$$ Recopier et compléter le tableau de valeurs suivant en exécutant cet algorithme. Arrondir les valeurs à $10^{-2}$ près. $$\begin{array}{|c| c|c|c|}\hline &\text{Initialisation }&\text{Étape 1}& \text{Étape 2}\\ \hline p &0,25 & &\\ \hline t &3,5 & &\\ \hline C &0,21 & &\\ \hline \end{array} $$ Que représente la valeur affichée par cet algorithme ?
   $\quad$
   $$\begin{array}{|c|c|c|c|}
   \hline
   &\text{Initialisation}&\text{Etape }1&\text{Etape }2\\
   \hline
   p&0,25&0,25&0,25 \\
   \hline
   t&3,5&3,75&4 \\
   \hline
   C&0,21&0,18&0,15\\
   \hline
   \end{array}$$
   L’algorithme affiche le temps, après l’ingestion d’alcool, à partir duquel la concentration d’alcool dans le sang n’est plus détectable (au quart d’heure près).
   $\quad$