Baccalauréat S Amérique du Sud 22 novembre 2016 - Correction Exercice 1

Page 2 sur 12: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

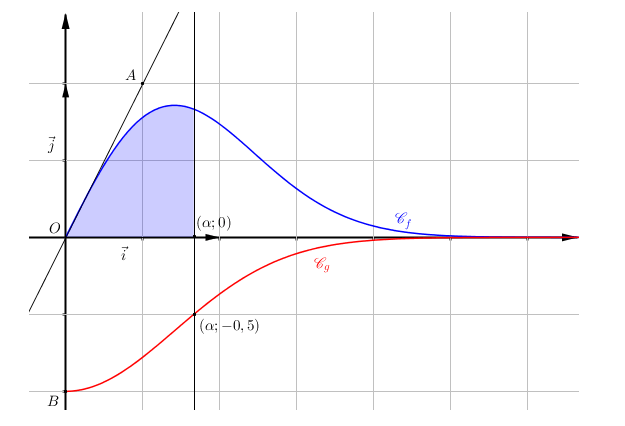
Les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ données en annexe 1 sont les représentations graphiques, dans un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, de deux fonctions $f$ et $g$ définies sur $[0~;~+ \infty[$. On considère les points A(0,5 ; 1) et B$(0 ; -1)$ dans le repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. On sait que O appartient à $\mathcal{C}_f$ et que la droite (OA) est tangente à $\mathcal{C}_f$ au point O.

1. On suppose que la fonction $f$ s'écrit sous la forme $f(x) = (ax + b)\text{e}^{- x^2}$ où $a$ et $b$ sont des réels. Déterminer les valeurs exactes des réels $a$ et $b$, en détaillant la démarche.
On peut lire que $f(0)=0$ et que $f'(0)=2$ (coefficient directeur de la tangente $(OA)$).
Or $f(0)=b$ donc $b=0$
La fonction $f$ est dérivable sur $[0;+\infty[$ en tant que produit et composition de fonctions dérivables sur cet intervalle.
On a $f(x)=ax\text{e}^{-x^2}$ car on vient de montrer que $b=0$.
$f'(x)=a\text{e}^{-x^2}-2ax^2\text{e}^{-x^2}$
Donc $f'(0)=a$. Par conséquent $a=2$.
$\quad$

Désormais, on considère que $f(x) = 2x\text{e}^{- x^2}$ pour tout $x$ appartenant à $[0~;~+ \infty[$

2. 1. On admettra que, pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$. Calculer $\displaystyle\lim_{x \to + \infty} f(x)$.
   $\lim\limits_{x \to +\infty} x^2=+\infty$ et $\lim\limits_{X \to +\infty} \dfrac{e^X}{X}=+\infty$.
   Donc $\lim\limits_{x \to +\infty} \dfrac{\text{e}^{x^2}}{x^2}=+\infty$ et $\lim\limits_{x \to +\infty} \dfrac{x^2}{\text{e}^{x^2}}=0$
   De plus $\lim\limits_{x \to +\infty} \dfrac{2}{x}=0$
   Par produit on a donc $\lim\limits_{x \to +\infty} f(x)=0$.
   $\quad$
   
   2. Dresser, en le justifiant, le tableau de variations de la fonction $f$ sur $[0~;~+ \infty[$.
   Pour tout réel $x\geq 0$, $f'(x)=2\text{e}^{-x^2}-4x^2\text{e}^{-x^2}=2(1-2x^2)\text{e}^{-x^2}$
   La fonction exponentielle est strictement positive sur $\mathbb R$ donc le signe de $f'(x)$ ne dépend que de celui de $1-2x^2$.
   Or $1-2x^2=\left(1-\sqrt{2}x\right)\times \left(1+\sqrt{x}\right)$.
   Sur $[0;+\infty[$ on a $\left(1+\sqrt{x}\right) >0$.
   $1-\sqrt{2}x=0 \iff x=\dfrac{1}{\sqrt{2}} \iff x=\dfrac{\sqrt{2}}{2}$
   On en déduit donc le tableau de variation suivant :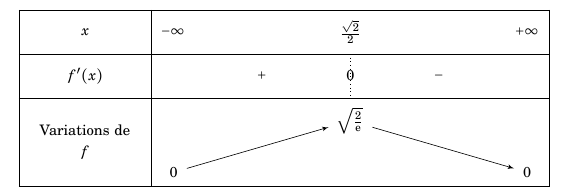
   $f \left(\frac{\sqrt{2}}{2} \right)=2\times \frac{\sqrt{2}}{2} \text{e}^{-\frac{1}{2}}= \sqrt 2 \times \frac{1}{\text{e}^{\frac{1}{2}}}= \sqrt{\frac{2}{\text{e}}} $
3. La fonction $g$ dont la courbe représentative $\mathcal{C}_g$ passe par le point B$(0~;~-1)$ est une primitive de la fonction $f$ sur $[0~;~+ \infty[$.
   1. Déterminer l'expression de $g(x)$.
   $f$ est de la forme $-u’\text{e}^{u}$.
   Donc une primitive de la fonction $f$ sur $[0;+\infty[$ est de la forme $g(x)=-\text{e}^{-x^2}+c$.
   On sait que $g(0)=-1$ puisque la courbe $\mathscr{C}_g$ passe par le point $B(0;-1)$.
   Or $g(0)=-1+c$.
   Par conséquent $-1+c=-1$ et $c=0$.
   On en déduit donc que, sur $[0;+\infty[$, une primitive de la fonction $f$ est la fonction $g$ définie par $g(x)=-\text{e}^{-x^2}$ dont la courbe représentative passe par le point $B$.
   $\quad$
   
   2. Soit $m$ un réel strictement positif. Calculer $I_m = \displaystyle\int_0^{m} f(t)\:\text{d}t$ en fonction de $m$.
   $\begin{align*} I_m&=\int_0^m f(t)\text{d}t \\ &=g(m)-g(0) \\ &=-\text{e}^{-m^2}+1
   \end{align*}$
   $\quad$
   
   3. Déterminer $\displaystyle\lim_{m \to + \infty} I_m$.
   $\lim\limits_{m \to +\infty} -m^2=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$ donc $\lim\limits_{m \to +\infty} e^{-x^2}=0$ et $\lim\limits_{m \to +\infty} I_m=1$
   $\quad$
4. 1. Justifier que $f$ est une fonction densité de probabilité sur $[0~;~+ \infty[$.
   Pour tout réel $x$ positif on a : $2x \geq 0$ et $\text{e}^{-x^2} \geq 0$ (car la fonction exponentielle est strictement positive).
   Par conséquent $f(x) \geq 0$. (on pouvait également utiliser le tableau de variation)
   $f$ est continue sur $[0;+\infty[$ en tant que produit de fonctions continues sur cet intervalle.
   De plus, d’après la question précédente, $\lim\limits_{m \to +\infty} \displaystyle \int_0^m f(t)\text{d}t = 0$.
   La fonction $f$ est donc une fonction densité de probabilité sur $[0;+\infty[$.
   $\quad$
   
   2. Soit $X$ une variable aléatoire continue qui admet la fonction $f$ comme densité de probabilité. Justifier que, pour tout réel $x$ de $[0~;~+ \infty[$, $P(X \leqslant x) = g(x) + 1$.
   Pour tout réel $x$ positif, on a :
   $P(X \leq x) = \displaystyle \int_0^x f(t)\text{d}t=g(x)-g(0)=g(x)+1$
   $\quad$
   
   3. En déduire la valeur exacte du réel $\alpha$ tel que $P(X \leqslant \alpha) = 0,5$.
   $\begin{align*} P(X \leq \alpha) = 0,5 &\iff g(\alpha)+1=0,5 \\ &\iff g(\alpha)=-0,5 \\ &\iff -\text{e}^{-\alpha^2}=-0,5 \\ &\iff \text{e}^{-\alpha^2}=0,5 \\ &\iff -\alpha^2 = \ln 0,5 \\ &\iff v^2=-\ln 0,5 \\ &\iff \alpha^2=- \left(-\ln 2\right) \\ &\iff \alpha^2=\ln 2 \\ &\iff \alpha=\sqrt{\ln 2} \text{ ou } \alpha=-\sqrt{\ln 2} \\ &\iff \alpha=\sqrt{\ln 2} \text{ car } \alpha \geq 0
   \end{align*}$
   $\quad$
   
   4. Sans utiliser une valeur approchée de $\alpha$, construire dans le repère de l'annexe 1 le point de coordonnées $(\alpha~;~0)$ en laissant apparents les traits de construction. Hachurer ensuite la région du plan correspondant à $P(X \leqslant \alpha)$.