Baccalauréat S Nouvelle-Calédonie Mars 2017 - Correction Exercice 5

Page 10 sur 10: Correction Exercice 5

Correction de l'exercice de Géométrie 5 points

Commun à tous les candidats

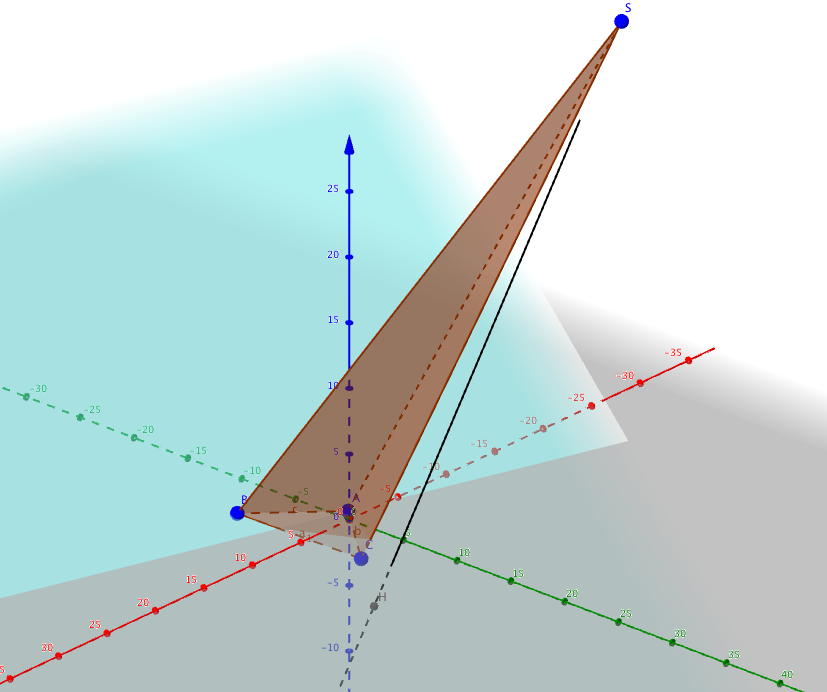
L'espace est muni d'un repère orthonormé $(O~;~I,~ J,~ K)$. On considère les points \[\text{A}(-1~;~-1~;~0),\: \text{B}(6~;~-5~;~1),\: \text{C}(1~;~2~;~-2) \:\:\text{et S}(13~;~37~;~54).\]

1. 1. Justifier que les points A, B et C définissent bien un plan.
   $\vec{AB}\begin{pmatrix}7\\-4\\1\end{pmatrix}$
   $\vec{AC}\begin{pmatrix}2\\3\\-2\end{pmatrix}$
   $\dfrac{7}{2} \neq \dfrac{-4}{3}$
   Les vecteurs $\vec{AB}$ et $\vec{AC}$ ne sont pas colinéaires et définissent donc bien un plan.
   $\quad$
   
   2. Prouver que le vecteur $\vec{n}\begin{pmatrix}5\\16\\29\end{pmatrix}$ est un vecteur normal au plan (ABC).
   $\vec{n}.\vec{AB}=5\times 7+16\times (-4)+29\times 1 =0$
   $\vec{n}.\vec{AC}=5\times 2+16\times 3+29\times (-2) =0$
   Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(ABC)$. C’est un vecteur normal au plan $(ABC)$.
   $\quad$
   
   3. En déduire une équation cartésienne du plan (ABC).
   Une équation cartésienne du plan $(ABC)$ est donc de la forme :
   $5x+16y+29z+d=0$.
   Le point $A(-1;-1;0)$ appartient au plan $(ABC)$.
   Par conséquent $-5-16+d=0 \iff d=21$.
   Une équation cartésienne du plan $(ABC)$ est donc $5x+16y+29z+21=0$.
2. 1. Déterminer la nature du triangle ABC.
   $\vec{AB}.\vec{AC}=14-12-2=0$.
   Le triangle $ABC$ est donc rectangle en $A$.
   Regardons s’il est également isocèle.
   $AB=\sqrt{49+16+1}=\sqrt{66}$
   $AC=\sqrt{4+9+4}=\sqrt{17}\neq AB$.
   Le triangle $ABC$ n’est donc pas isocèle.
   $\quad$
   
   2. Démontrer que la valeur exacte de l'aire du triangle ABC est, en unités d'aire, $\dfrac{\sqrt{1122}}{2}$.
   L’aire du triangle $ABC$ est donc :
   $\begin{align*} \mathscr{A}&=\dfrac{AB\times AC}{2}\\
   &=\dfrac{\sqrt{66}\times \sqrt{17}}{2} \\
   &=\dfrac{\sqrt{1~122}}{2}
   \end{align*}$
   $\quad$
3. 1. Prouver que les points A, B, C et S ne sont pas coplanaires.
   Regardons si les coordonnées du point $S(13;37;54)$ vérifient l’équation cartésienne du plan $(ABC)$.
   $5\times 13+16\times 37+29\times 54+21=2~244\neq 0$.
   Le point $S$ n’appartient donc pas au plan $(ABC)$ : les points $A,B,C$ et $S$ ne sont pas coplanaires.
   $\quad$
   
   2. La droite $(\Delta)$ perpendiculaire au plan (ABC) passant par le point S coupe le plan (ABC) en un point noté H. Déterminer les coordonnées du point H.
   La droite $(\Delta)$ est perpendiculaire au plan $(ABC)$. Le vecteur $\vec{n}$ est donc un vecteur directeur de la droite $(\Delta)$.
   Un représentation paramétrique de la droite $(\Delta)$ est donc :
   $\begin{cases} x=13+5t \\y=37+16t \qquad t\in \mathbb R \\z=54+29t\end{cases}$
   Les coordonnées du point $H$, point d’intersection du plan $(ABC)$ et de la droite $(\Delta)$ sont donc solution du système :
   $\begin{cases} x=13+5t \\y=37+16t \\z=54+29t\\5x+16y+29z+21=0\end{cases}$
   $\iff \begin{cases} x=13+5t \\y=37+16t \\z=54+29t\\5(13+5t)+16(37+16t)+29(54+29t)+21=0\end{cases}$
   $\iff \begin{cases} x=13+5t \\y=37+16t \\z=54+29t\\65+25t+592+256t+1~566+841t+21=0\end{cases} $
   $\iff \begin{cases} x=13+5t \\y=37+16t \\z=54+29t\\1~122t+2~244=0\end{cases} $
   $\iff \begin{cases} x=13+5t \\y=37+16t \\z=54+29t\\t=-2\end{cases} $
   $\iff \begin{cases} t=-2\\x=3\\y=5 \\z=-4\end{cases} $
   Le point $H$ a donc pour coordonnées $(3;5;-4)$.
   $\quad$
4. Déterminer le volume du tétraèdre SABC.
   On rappelle que le volume d’une pyramide est donné par \[\dfrac{\text{ Aire de la base} \times \text{ hauteur} }{3}.\]
Calculons tout d’abord $SH=\sqrt{(3-13)^2+(37-5)^2+(-4-54)^2}=\sqrt{4~488}$
Le volume du tétraèdre $SABC$ est donc :
$\begin{align*} \mathscr{V}&=\dfrac{\mathscr{A}\times SH}{3} \\
&=\dfrac{\dfrac{\sqrt{1122}}{2}\times \sqrt{4~488}}{3}\\
&=374
\end{align*}$
$\quad$