Baccalauréat S Pondichéry 26 Avril 2017
Exercice 1 5 points
Les parties A, B et C peuvent être traitées de façon indépendante. Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième. La chocolaterie « Choc'o » fabrique des tablettes de chocolat noir, de 100 grammes, dont la teneur en cacao annoncée est de 85 %.
Partie A
À l'issue de la fabrication, la chocolaterie considère que certaines tablettes ne sont pas commercialisables : tablettes cassées, mal emballées, mal calibrées, etc. La chocolaterie dispose de deux chaînes de fabrication:
- la chaîne A, lente, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est égale à 0,98.
- la chaîne B, rapide, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est 0,95.
À la fin d'une journée de fabrication, on prélève au hasard une tablette et on note : $A$ l' évènement: « la tablette de chocolat provient de la chaîne de fabrication A » ; $C$ l'évènement : « la tablette de chocolat est commercialisable ». On note $x$ la probabilité qu'une tablette de chocolat provienne de la chaîne A.
- Montrer que $P(C) = 0,03x+ 0,95$.
- À l'issue de la production, on constate que 96 % des tablettes sont commercialisables et on retient cette valeur pour modéliser la probabilité qu'une tablette soit commercialisable. Justifier que la probabilité que la tablette provienne de la chaîne B est deux fois égale à celle que la tablette provienne de la chaîne A.
Partie B
Une machine électronique mesure la teneur en cacao d'une tablette de chocolat. Sa durée de vie, en années, peut être modélisée par une variable aléatoire $Z$ suivant une loi exponentielle de paramètre $\lambda$.
- La durée de vie moyenne de ce type de machine est de 5 ans. Déterminer le paramètre $\lambda$ de la loi exponentielle.
- Calculer $P(Z> 2)$.
- Sachant que la machine de l'atelier a déjà fonctionné pendant 3 ans, quelle est la probabilité que sa durée de vie dépasse 5 ans ?
Partie C
On note $X$ la variable aléatoire donnant la teneur en cacao, exprimée en pourcentage, d'une tablette de 100 g de chocolat commercialisable. On admet que X suit la loi normale d'espérance $\mu = 85$ et d'écart type $\sigma = 2$.
- Calculer $P(83 < X < 87)$. Quelle est la probabilité que la teneur en cacao soit différente de plus de 2 % du pourcentage annoncé sur l'emballage ?
- Déterminer une valeur approchée au centième du réel $a$ tel que: \[P(85 - a < X < 85 + a) = 0,9 .\] Interpréter le résultat dans le contexte de l'exercice.
- La chocolaterie vend un lot de 10000 tablettes de chocolat à une enseigne de la grande distribution. Elle affirme au responsable achat de l'enseigne que, dans ce lot, 90 % des tablettes ont un pourcentage de cacao appartenant à l'intervalle [81,7 ; 88,3]. Afin de vérifier si cette affirmation n'est pas mensongère, le responsable achat fait prélever $550$ tablettes au hasard dans le lot et constate que, sur cet échantillon, $80$ ne répondent pas au critère. Au vu de l'échantillon prélevé, que peut-on conclure quant à l'affirmation de la chocolaterie ?
Correction de l'exercice 1 (6 points)
Les parties A, B et C peuvent être traitées de façon indépendante. Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième. La chocolaterie « Choc'o » fabrique des tablettes de chocolat noir, de 100 grammes, dont la teneur en cacao annoncée est de 85 %.
Partie A
À l'issue de la fabrication, la chocolaterie considère que certaines tablettes ne sont pas commercialisables : tablettes cassées, mal emballées, mal calibrées, etc. La chocolaterie dispose de deux chaînes de fabrication:
- la chaîne A, lente, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est égale à 0,98.
- la chaîne B, rapide, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est 0,95.
À la fin d'une journée de fabrication, on prélève au hasard une tablette et on note : $A$ l' évènement: « la tablette de chocolat provient de la chaîne de fabrication A » ; $C$ l'évènement : « la tablette de chocolat est commercialisable ». On note $x$ la probabilité qu'une tablette de chocolat provienne de la chaîne A.
- Montrer que $P(C) = 0,03x+ 0,95$.
- À l'issue de la production, on constate que 96\,\% des tablettes sont commercialisables et on retient cette valeur pour modéliser la probabilité qu'une tablette soit commercialisable. Justifier que la probabilité que la tablette provienne de la chaîne B est deux fois égale à celle que la tablette provienne de la chaîne A. On sait que :
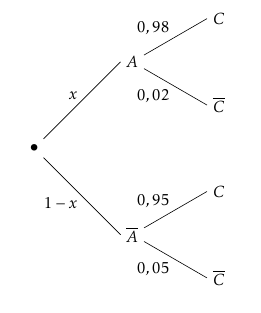 $\begin{align*} p(C)&=p(A\cap C)+p\left(\overline{A}\cap C\right) \\
$\begin{align*} p(C)&=p(A\cap C)+p\left(\overline{A}\cap C\right) \\&=0,98x+0,95(1-x)\\
&=0,98x+0,95-0,95x\\
&=0,03x+0,95
\end{align*}$
$\quad$
$\begin{align*} p(C)=0,96 &\iff 0,03x+0,95=0,96\\
&\iff 0,03x=0,01\\
&\iff x = \dfrac{1}{3}
\end{align*}$
Ainsi $p(A)=\dfrac{1}{3}$ et $p(B)=1-\dfrac{1}{3}$ $=\dfrac{2}{3}$ $=2p(A)$.
$\quad$
Partie B
Une machine électronique mesure la teneur en cacao d'une tablette de chocolat. Sa durée de vie, en années, peut être modélisée par une variable aléatoire $Z$ suivant une loi exponentielle de paramètre $\lambda$.
- La durée de vie moyenne de ce type de machine est de 5 ans. Déterminer le paramètre $\lambda$ de la loi exponentielle. On sait que $E(Z)=5$ or $E(Z)=\dfrac{1}{\lambda}$
- Calculer $P(Z> 2)$. $P(Z>2)=\text{e}^{-0,2\times 2}=\text{e}^{-0,4}$
- Sachant que la machine de l'atelier a déjà fonctionné pendant 3 ans, quelle est la probabilité que sa durée de vie dépasse 5 ans ? On veut calculer $P_{Z\geqslant 3}(Z\geqslant 5)=P_{Z\geqslant 3}(Z\geqslant 3+2)$.
Par conséquent $\dfrac{1}{\lambda}=5 \iff \lambda = \dfrac{1}{5}=0,2$.
$\quad$
Les lois exponentielles sont sans vieillissement.
Par conséquent :$P_{Z\geqslant 3}(Z\geqslant 3+2)=P(Z\geqslant 2)=\text{e}^{-0,4}$.
$\quad$
Partie C
On note $X$ la variable aléatoire donnant la teneur en cacao, exprimée en pourcentage, d'une tablette de 100 g de chocolat commercialisable. On admet que X suit la loi normale d'espérance $\mu = 85$ et d'écart type $\sigma = 2$.
- Calculer $P(83 < X < 87)$.
Quelle est la probabilité que la teneur en cacao soit différente de plus de 2 % du pourcentage annoncé sur l'emballage ? A l’aide de la calculatrice on trouve $P(83 \leqslant X \leqslant 87)\approx 0,683$. - Déterminer une valeur approchée au centième du réel $a$ tel que: \[P(85 - a < X < 85 + a) = 0,9 .\] Interpréter le résultat dans le contexte de l'exercice. $\quad$
- La chocolaterie vend un lot de 10000 tablettes de chocolat à une enseigne de la grande distribution. Elle affirme au responsable achat de l'enseigne que, dans ce lot, 90 % des tablettes ont un pourcentage de cacao appartenant à l'intervalle [81,7 ; 88,3]. Afin de vérifier si cette affirmation n'est pas mensongère, le responsable achat fait prélever $550$ tablettes au hasard dans le lot et constate que, sur cet échantillon, $80$ ne répondent pas au critère. Au vu de l'échantillon prélevé, que peut-on conclure quant à l'affirmation de la chocolaterie ?
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
La probabilité que la teneur en cacao soit différente de plus de $2\%$ du pourcentage annoncé sur l’emballage est :
$1-P(83 \leqslant X\leqslant 87) \approx 0,317$.
$\quad$
$\begin{align*} P(85-a\leqslant X\leqslant 85+a)=0,9&\iff P(-a\leqslant X-85\leqslant a)=0,9 \\
&\iff P\left(-\dfrac{a}{2}\leqslant \dfrac{X-85}{2}\leqslant \dfrac{a}{2}\right)=0,9
\end{align*}$
La variable aléatoire $Z=\dfrac{X-85}{2}$ suit la loi normale centrée réduite.
Par conséquent :
$\begin{align*} P\left(-\dfrac{a}{2}\leqslant \dfrac{X-85}{2}\leqslant \dfrac{a}{2}\right)=0,9 &\iff P\left(-\dfrac{a}{2}\leqslant Z\leqslant \dfrac{a}{2}\right)=0,9 \\
&\iff 2P\left(Z\leqslant \dfrac{a}{2}\right)-1=0,9\\
&\iff 2P\left(Z\leqslant \dfrac{a}{2}\right)=1,9\\
&\iff P\left(Z\leqslant \dfrac{a}{2}\right)=0,95
\end{align*}$
A l’aide de la touche Inverse loi normale de la calculatrice on trouve : $\dfrac{a}{2}\approx 1,645$
Par conséquent $a\approx 3,29$.
2ND DISTR 3Fracnormale( $\1 $ )EXE
Avec une calculatrice de type TI
$$Fracnormale( \1 ) \approx \2$$
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
\end{align*}$
La fréquence observée de tablettes répondant au critère annoncé est $f=\dfrac{550-80}{550}\approx 0,855 \notin I_{10~000}$.
Au risque d’erreur de $5\%$ on peut remettre en cause l’affirmation du responsable achat de l’enseigne.
$\quad$
Exercice 2 3 points
On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
- On considère l'équation \[(E) :\qquad z^2 - 6z + c = 0\] où $c$ est un réel strictement supérieur à 9.
- Justifier que (E) admet deux solutions complexes non réelles.
- Justifier que les solutions de (E) sont $z_{\text{A}} = 3 + \text{i}\sqrt{c - 9}$ et $z_{\text{B}} = 3 - \text{i}\sqrt{c - 9}$.
- On note A et B les points d'affixes respectives $z_{\text{A}}$ et $z_{\text{B}}$. Justifier que le triangle OAB est isocèle en O.
- Démontrer qu'il existe une valeur du réel $c$ pour laquelle le triangle OAB est rectangle et déterminer cette valeur.
Correction de l'exercice 2 (3 points)
On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
- On considère l'équation \[(E) :\qquad z^2 - 6z + c = 0\] où $c$ est un réel strictement supérieur à 9.
- Justifier que (E) admet deux solutions complexes non réelles. On considère l’équation $z^2-6z+c=0$
- Justifier que les solutions de (E) sont $z_{\text{A}} = 3 + \text{i}\sqrt{c - 9}$ et $z_{\text{B}} = 3 - \text{i}\sqrt{c - 9}$. Les solutions sont donc :
Son discriminant est $\Delta=36-4c=4(9-c)$
On sait que $c>9$. Par conséquent $\Delta <0$.
L’équation $(E)$ admet donc deux solutions complexes non réelles.
$\quad$
$z_1=\dfrac{6-\text{i}\sqrt{4(c-9)}}{2}=\dfrac{6-2\text{i}\sqrt{c-9}}{2}=3-\text{i}\sqrt{c-9}$ et $z_2=\overline{z_1}=3+\text{i}\sqrt{c-9}$.
$\quad$ - On note A et B les points d'affixes respectives $z_{\text{A}}$ et $z_{\text{B}}$. Justifier que le triangle OAB est isocèle en O. $OA=\left|z_A\right|=\sqrt{9+c-9}=\sqrt{c}$
- Démontrer qu'il existe une valeur du réel $c$ pour laquelle le triangle OAB est rectangle et déterminer cette valeur. $AB=\left|z_A-z_B\right|=\left|2\text{i}\sqrt{c-9}\right|=2\sqrt{(c-9)}$.
$OB=\left|z_B\right|=\sqrt{9+c-9}=\sqrt{c}$
Le triangle $OAB$ est donc isocèle en $O$.
$\quad$ $\quad$
Le triangle $OAB$ est rectangle en $O$
$\iff AB^2=OA^2+OB^2$
$\iff 4(c-9)=2c$
$\iff 4c-36=2c$
$\iff 2c-36=0$
$\iff c=18$
Il existe donc bien une seule valeur du réel $c$ pour laquelle le triangle $OAB$ est rectangle et $c=18$.
Exercice 3 4 points
Une entreprise spécialisée dans les travaux de construction a été mandatée pour percer un tunnel à flanc de montagne. Après étude géologique, l'entreprise représente dans le plan la situation de la façon suivante : dans un repère orthonormal, d'unité 2 m, la zone de creusement est la surface délimitée par l'axe des abscisses et la courbe $\mathcal{C}$.
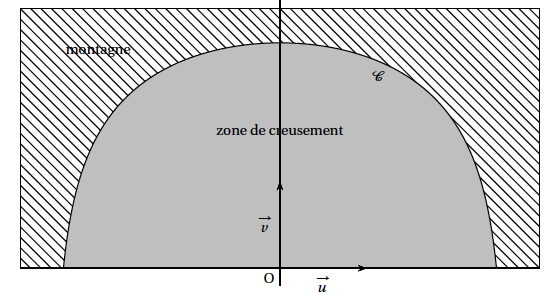
On admet que $\mathcal{C}$ est la courbe représentative de la fonction $f$ définie sur l'intervalle $[- 2,5~;~2,5]$ par: \[f(x) = \ln \left(- 2x^2 + 13,5\right).\] L'objectif est de déterminer une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
Partie A : Étude de la fonction $f$
- Calculer $f ‘(x)$ pour $x \in [- 2,5~;~2,5]$.
- Dresser, en justifiant, le tableau de variation de la fonction $f$ sur $[- 2,5~;~2,5]$. En déduire le signe de $f$ sur $[- 2,5~;~2,5]$.
Partie B : Aire de la zone de creusement
On admet que la courbe $\mathcal{C}$ est symétrique par rapport à l'axe des ordonnées du repère.
- La courbe $\mathcal{C}$ est-elle un arc de cercle de centre 0 ? Justifier la réponse.
- Justifier que l'aire, en mètre carré, de la zone de creusement est $\mathcal{A} = 8\displaystyle\int_0^{2,5} f(x)\:\text{d}x$.
- L'algorithme, donné en annexe, permet de calculer une valeur approchée par défaut de $I = \displaystyle\int_0^{2,5} f(x)\:\text{d}x$, notée $a$. On admet que : $a \leqslant I \leqslant a + \dfrac{f(0) - f(2,5)}{n}\times 2,5$.
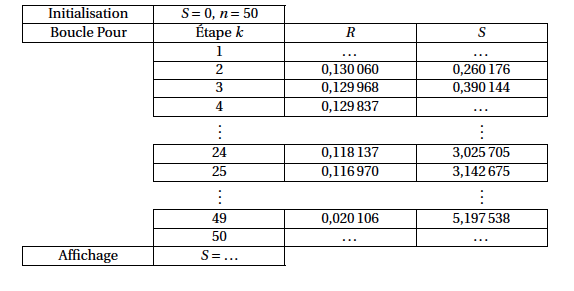
- Le tableau fourni en annexe, donne différentes valeurs obtenues pour R et S lors de l'exécution de l'algorithme pour $n = 50$. Compléter ce tableau en calculant les six valeurs manquantes.
- En déduire une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
$$\begin{array}{|l|}\hline \text{Variables}\\ \hspace{1cm}\begin{array}{|l} R \text{ et } S \text{ sont des réels}\\ n \text{ et }k \text{ sont des entiers}\\ \end{array}\\ \text{Traitement} \\ \hspace{1cm}\begin{array}{|l} S \text{ prend la valeur } 0\\ \text{ Demander la valeur de } n\\ \text{Pour } k \text{ variant de } 1 \text{ à } n \text{ faire }\\ \hspace{1cm}\begin{array}{|l} R \text{ prend la valeur } \dfrac{2,5}{n} \times f\left(\dfrac{2,5}{n}\times k \right)\\ S \text{ prend la valeur } S + R\\ \end{array}\\ \text{ Fin Pour}\\ \text{ Afficher } S\\ \end{array}\\ \hline \end{array}$$ Le tableau ci-dessous donne les valeurs de $R$ et de $S$, arrondies à $10^{-6}$, obtenues lors de l'exécution de l'algorithme pour $n = 50$.
Correction de l'exercice 3 (5 points)
Une entreprise spécialisée dans les travaux de construction a été mandatée pour percer un tunnel à flanc de montagne. Après étude géologique, l'entreprise représente dans le plan la situation de la façon suivante : dans un repère orthonormal, d'unité 2 m, la zone de creusement est la surface délimitée par l'axe des abscisses et la courbe $\mathcal{C}$.

On admet que $\mathcal{C}$ est la courbe représentative de la fonction $f$ définie sur l'intervalle $[- 2,5~;~2,5]$ par: \[f(x) = \ln \left(- 2x^2 + 13,5\right).\] L'objectif est de déterminer une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
Partie A : Étude de la fonction $f$
- Calculer $f ‘(x)$ pour $x \in [- 2,5~;~2,5]$. On appelle $u$ la fonction définie sur $[-2,5;2,5]$ par $u(x)=-2x^2+13,5$.
- Dresser, en justifiant, le tableau de variation de la fonction $f$ sur $[- 2,5~;~2,5]$. En déduire le signe de $f$ sur $[- 2,5~;~2,5]$. Puisque $-2x^2+13,5>0$ sur l’intervalle $[2,5;2,5]$ le signe de $f'(x)$ ne dépend que de celui de $-4x$.
La fonction $u$ est dérivable sur cet intervalle en tant que polynôme et, de par la définition de la fonction $f$, est également strictement positive sur cet intervalle.
Par composition des fonctions, la fonction $f$ est dérivable sur l’intervalle $[-2,5;2,5]$
$f(x)=\ln\left(u(x)\right)$ donc $f'(x)=\dfrac{u'(x)}{u(x)}$.
$f'(x)=\dfrac{-4x}{-2x^2+13,5}$
$\quad$
Ainsi $f'(x)>0$ sur l’intervalle $[-2,5;0]$ et $f'(x)>0$ sur l’intervalle $[0;2,5]$.
On obtient alors le tableau de variation suivant :
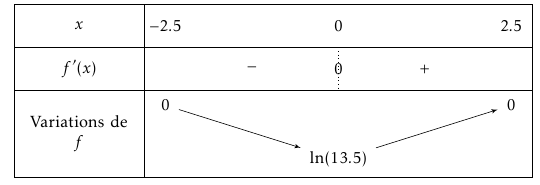
Partie B : Aire de la zone de creusement
On admet que la courbe $\mathcal{C}$ est symétrique par rapport à l'axe des ordonnées du repère.
- La courbe $\mathcal{C}$ est-elle un arc de cercle de centre 0 ? Justifier la réponse. La hauteur du tunnel est $h=\ln(13,5)\approx 2,6$.
- Justifier que l'aire, en mètre carré, de la zone de creusement est $\mathcal{A} = 8\displaystyle\int_0^{2,5} f(x)\:\text{d}x$. Par symétrie $\mathscr{A}$ est le double de l’aire comprise entre la courbe $\mathscr{C}$, l’axe des abscisses, la droite d’équation $x=0$ et celle d’équation $x=2,5$.
- L'algorithme, donné en annexe, permet de calculer une valeur approchée par défaut de $I = \displaystyle\int_0^{2,5} f(x)\:\text{d}x$, notée $a$. On admet que : $a \leqslant I \leqslant a + \dfrac{f(0) - f(2,5)}{n}\times 2,5$.
- Le tableau fourni en annexe, donne différentes valeurs obtenues pour R et S lors de l'exécution de l'algorithme pour $n = 50$. Compléter ce tableau en calculant les six valeurs manquantes. A l’étape $1$ on a $R=0,130~116$ et $S=0,130~116$
- En déduire une valeur approchée, au mètre carré près, de l'aire de la zone de creusement. Une valeur approchée de $\displaystyle \int_0^{2,5} f(x)\text{d}x$ est $5,197~538$.
A l’étape $4$ on a $S=0,519~981$
A l’étape $50$ on a $R=0$ et $S=5,197~538$
A l’affichage $S=5,197~538$
$\quad$
Par conséquent une valeur approchée de la zone de creusement est :
$\mathscr{A}\approx 8\times 5,197~538$
Soit $\mathscr{A} \approx 41,580~304 \approx 42$ m$^2$.
$\quad$
La largeur du tunnel est $\ell = 2,5\times 2=5 \neq 2h$.
La courbe $\mathscr{C}$ n’est donc pas un arc de cercle de centre $O$.
$\quad$
Donc :
$\begin{align*} \mathscr{A}&=\displaystyle 2\int_0^{2,5}f(x)\text{d}x~~ \text{u.a.} \\
&=2\int_0^{2,5}f(x)\text{d}x\times 2^2 \text{ m}^2 \\
&=8\int_0^{2,5}f(x)\text{d}x\text{ m}^2
\end{align*}$
$\quad$
$$\begin{array}{|l|}\hline \text{Variables}\\ \hspace{1cm}\begin{array}{|l} R \text{ et } S \text{ sont des réels}\\ n \text{ et }k \text{ sont des entiers}\\ \end{array}\\ \text{Traitement} \\ \hspace{1cm}\begin{array}{|l} S \text{ prend la valeur } 0\\ \text{ Demander la valeur de } n\\ \text{Pour } k \text{ variant de } 1 \text{ à } n \text{ faire }\\ \hspace{1cm}\begin{array}{|l} R \text{ prend la valeur } \dfrac{2,5}{n} \times f\left(\dfrac{2,5}{n}\times k \right)\\ S \text{ prend la valeur } S + R\\ \end{array}\\ \text{ Fin Pour}\\ \text{ Afficher } S\\ \end{array}\\ \hline \end{array}$$ Le tableau ci-dessous donne les valeurs de $R$ et de $S$, arrondies à $10^{-6}$, obtenues lors de l'exécution de l'algorithme pour $n = 50$.

Exercice 4 5 points
On considère deux suites $\left(u_n\right)$ et $\left(v_n\right)$ :
- la suite $\left(u_n\right)$ définie par $u_0 = 1$ et pour tout entier naturel $n$ :$\: u_{n+1} = 2u_n - n + 3$ ;
- la suite $\left(v_n\right)$ définie, pour tout entier naturel $n$, par $v_n = 2^n$.
Partie A : Conjectures
Florent a calculé les premiers termes de ces deux suites à l'aide d'un tableur. Une copie d'écran est donnée ci-dessous. $$\begin{array}{|c|c|c|c|}\hline &A &B &C\\ \hline 1 &\text{rang } n &\text{ terme } u_n &\text{ terme }v_n \\ \hline 2 &0 & 1 &1 \\ \hline 3 &1 &5 &2\\ \hline 4 &2 &12 &4\\ \hline 5 &3 &25 &8 \\ \hline 6 &4 &50 &16\\ \hline \end{array} $$
- Quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir par copie vers le bas les termes des deux suites ?
- Pour les termes de rang 10, 11, 12 et 13 Florent obtient les résultats suivants : $$ \begin{array}{|c|c|c|c|}\hline 12 &10 & 3080 & 1024 \\ \hline 13 &11 & 6153 & 2048 \\ \hline 14 &12 & 12298 & 4096 \\ \hline 15 &l3 & 24587 & 8192 \\ \hline \end{array} $$ Conjecturer les limites des suites $\left(u_n\right)$ et $\left(\dfrac{u_n}{v_n} \right)$.
Partie B : Étude de la suite $\left(u_n\right)$
- Démontrer par récurrence que, pour tout entier naturel n, on a $u_n = 3 \times 2^n + n - 2$.
- Déterminer la limite de la suite $\left(u_n\right)$.
- Déterminer le rang du premier terme de la suite supérieur à 1 million.
Partie C : Étude de la suite $\left(\dfrac{u_n}{v_n} \right)$
- Démontrer que la suite $\left(\dfrac{u_n}{v_n} \right)$ est décroissante à partir du rang 3.
- On admet que, pour tout entier $n$ supérieur ou égal à 4, on a : $0 < \dfrac{n}{2^n} < \dfrac{1}{n}$. Déterminer la limite de la suite $\left(\dfrac{u_n}{v_n} \right)$ .
Correction de l'exercice 4 5 points
On considère deux suites $\left(u_n\right)$ et $\left(v_n\right)$ :
- la suite $\left(u_n\right)$ définie par $u_0 = 1$ et pour tout entier naturel $n$ :$\: u_{n+1} = 2u_n - n + 3$ ;
- la suite $\left(v_n\right)$ définie, pour tout entier naturel $n$, par $v_n = 2^n$.
Partie A : Conjectures
Florent a calculé les premiers termes de ces deux suites à l'aide d'un tableur. Une copie d'écran est donnée ci-dessous. $$\begin{array}{|c|c|c|c|}\hline &A &B &C\\ \hline 1 &\text{rang } n &\text{ terme } u_n &\text{ terme }v_n \\ \hline 2 &0 & 1 &1 \\ \hline 3 &1 &5 &2\\ \hline 4 &2 &12 &4\\ \hline 5 &3 &25 &8 \\ \hline 6 &4 &50 &16\\ \hline \end{array} $$
- Quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir par copie vers le bas les termes des deux suites ? En B3 on a pu saisir : $=2*B2-A2+3$
- Pour les termes de rang 10, 11, 12 et 13 Florent obtient les résultats suivants : $$ \begin{array}{|c|c|c|c|}\hline 12 &10 & 3080 & 1024 \\ \hline 13 &11 & 6153 & 2048 \\ \hline 14 &12 & 12298 & 4096 \\ \hline 15 &l3 & 24587 & 8192 \\ \hline \end{array} $$ Conjecturer les limites des suites $\left(u_n\right)$ et $\left(\dfrac{u_n}{v_n} \right)$. Il semblerait que la limite de la suite $\left(u_n\right)$ soit $+\infty$.
En $C3$ on a pu saisir : $=2^{A3}$
$\quad$
$\dfrac{3~080}{1~024}\approx 3,008$
$\dfrac{6~153}{2~048}\approx 3,004$
$\dfrac{12~298}{4~096}\approx 3,002$
$\dfrac{24~587}{8~192}\approx 3,001$
Il semblerait que la limite de la suite $\left(\dfrac{u_n}{v_n}\right)$ soit $3$.
$\quad$
Partie B : Étude de la suite $\left(u_n\right)$
- Démontrer par récurrence que, pour tout entier naturel n, on a $u_n = 3 \times 2^n + n - 2$. Initialisation : Si $n=0$ alors $u_0=1$ et $3\times 2^0-0-2=3-2=1$
- Déterminer la limite de la suite $\left(u_n\right)$. $2>1$ donc $\lim\limits_{n\to +\infty}2^n=+\infty$ et $\lim\limits_{n\to +\infty}3\times 2^n=+\infty$
- Déterminer le rang du premier terme de la suite supérieur à 1 million. On cherche la plus petite valeur de $n$ telle que $ u_n\geqslant 10^6$
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n=3\times 2^n+n-2$
$\begin{align*} u_{n+1}&=2u_n-n+3\\
&=2\left(3\times 2^n+n-2\right)-n+3\\
&=3\times 2^{n+1}+2n-4-n+3\\
&=3\times 2^{n+1}+n-1\\
&=3\times 2^{n+1}+(n+1)-2
\end{align*}$
La propriété est donc vraie au rang $n+1$
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $u_n=3\times 2^n+n-2$.
$\quad$
De plus $\lim\limits_{n\to +\infty}n-2=+\infty$
Par somme de limite $\lim\limits_{n\to +\infty}u_n=+\infty$
$\quad$
Les suites de terme général $\left(3\times 2^n\right)$ et $(n-2)$ sont croissantes. Par conséquent la suite $\left(u_n\right)$ est également croissante.
On a $u_{18}=786~448$ et $u_{19}=1~572~881$
Par conséquent c’est à partir du rang $19$ que $u_n\geqslant 10^6$.
$\quad$
Partie C : Étude de la suite $\left(\dfrac{u_n}{v_n} \right)$
- Démontrer que la suite $\left(\dfrac{u_n}{v_n} \right)$ est décroissante à partir du rang 3. On note $w_n=\dfrac{u_n}{v_n}$
- On admet que, pour tout entier $n$ supérieur ou égal à 4, on a : $0 < \dfrac{n}{2^n} < \dfrac{1}{n}$. Déterminer la limite de la suite $\left(\dfrac{u_n}{v_n} \right)$ . $\quad$
$\begin{align*}w_{n+1}-w_n&=\dfrac{3\times 2^{n+1}+n-1}{2^{n+1}}-\dfrac{3\times 2^n+n-2}{2^n} \\
&=3+\dfrac{n-1}{2^{n+1}}-3-\dfrac{n-2}{2^n}\\
&=\dfrac{n-1}{2^{n+1}}-\dfrac{2(n-2}{2^{n+1}}\\
&=\dfrac{n-1-2n+4}{2^{n+1}}\\
&=\dfrac{3-n}{2^{n+1}}
\end{align*}$
Par conséquent, si $n\geqslant 3$ alors $w_{n+1}-w_n\leqslant 0$ et la suite $\left(\dfrac{u_n}{v_n}\right)$ est décroissante.
$\quad$
$\begin{align*} \dfrac{u_n}{v_n}&=3-\dfrac{n-2}{2^n}\\
&=3-\dfrac{n}{2^n}+\dfrac{2}{2^n} \\
&=3-\dfrac{n}{2^n}+2\left(\dfrac{1}{2}\right)^n
\end{align*}$
$\lim\limits_{n \to +\infty} \dfrac{1}{n}=0$
D’après le théorème des gendarmes $\lim\limits_{n \to +\infty} \dfrac{n}{2^n}=0$
$-1<\dfrac{1}{2}<1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{1}{2}\right)^n=0$
Ainsi, par somme des limites $\lim\limits_{n \to +\infty} \dfrac{u_n}{v_n}=3$
Spécialité 5 points
On définit les suites $\left(u_n\right)$ et $\left(v_n\right)$ par : \[u_0 = v_0 = 1\: \text{et, pour tout entier naturel }\:n,\: u_{n+1} = 2u_n + 3v_n\: \text{et}\: v_{n+1} = 2u_n + v_n.\] On admettra que les termes de ces suites sont des entiers naturels non nuls.
Partie A : Conjectures
Flore a calculé les premiers termes des suites à l'aide d'un tableur. Une copie d'écran est donnée ci-dessous. $$\begin{array}{|c|c|c|c|}\hline &A &B &C\\ \hline 1 &\text{rang } n &\text{ terme } u_n &\text{ terme }v_n \\ \hline 2& 0 &1 &1\\ \hline 3& 1 &5 &3\\ \hline 4& 2 &19 &13\\ \hline 5& 3 &77 &51\\ \hline 6& 4 &307 &205\\ \hline \end{array} $$
- Quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir par copie vers le bas les termes des suites ?
- Soit $n$ un entier naturel. Conjecturer la valeur de PGCD$\left(u_n~;~v_n\right)$. Aucune justification n'est demandée.
- Pour les termes de rang 10, 11, 12 et 13 Flore obtient les résultats suivants : $$\begin{array}{|c|c|c|c|}\hline 12 &10 & 1258291 &838861\\ \hline 13 &Il &5033165 &3355443\\ \hline 14 &12 &20132659 &13421773\\ \hline 15 &13 &80530637 &53687091\\ \hline \end{array}$$ Elle émet la conjecture : « la suite $\left(\dfrac{u_n}{v_n} \right)$ converge ». Qu'en penser ?
Partie B : Étude arithmétique
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $2u_n - 3v_n = (- 1)^{n+1}$.
- Soit $n$ un entier naturel. Déduire de la question précédente la valeur de PGCD$\left(u_n~;~v_n\right)$.
Partie C : Étude matricielle
Pour tout entier naturel $n$, on définit :
- la matrice colonne $X_n = \begin{pmatrix}u_n\\ v_n\end{pmatrix}$,
- les matrices carrées $P = \begin{pmatrix} 1&3\\- 1&2\end{pmatrix}$ et $Q_n = \begin{pmatrix}(- 1)^n&3 \times 2^{2n}\\(- 1)^{n+1}&2^{2n+1}\end{pmatrix}.$
-
- Montrer que la matrice $\dfrac{1}{5}\begin{pmatrix}2&- 3\\1&1\end{pmatrix}$ est l'inverse de $P$.
- On admet que, pour tout entier naturel $n$, on a $X_n = Q_nP^{-1} X_0$. Démontrer que, pour tout entier naturel $n$, on a $\left\{\begin{array}{l c l} u_n&=&\dfrac{(- 1)^{n+1}+ 3\times 2^{2n+1}}{5}\\ v_n&=&\dfrac{(- 1)^{n}+ 2^{2n+2}}{5} \end{array}\right.$
-
- Vérifier que, pour tout entier naturel $n$, on a $\dfrac{u_n}{v_n}= \dfrac{\frac{(- 1)^{n+1}}{2^{2n+1}}+ 3}{\frac{(- 1)^{n}}{2^{2n+1}}+ 2}$.
- En déduire la limite de la suite $\left(\dfrac{u_n}{v_n} \right)$.
Correction de l'exercice de Spécialité 5 points
On définit les suites $\left(u_n\right)$ et $\left(v_n\right)$ par : \[u_0 = v_0 = 1\: \text{et, pour tout entier naturel }\:n,\: u_{n+1} = 2u_n + 3v_n\: \text{et}\: v_{n+1} = 2u_n + v_n.\] On admettra que les termes de ces suites sont des entiers naturels non nuls.
Partie A : Conjectures
Flore a calculé les premiers termes des suites à l'aide d'un tableur. Une copie d'écran est donnée ci-dessous. $$\begin{array}{|c|c|c|c|}\hline &A &B &C\\ \hline 1 &\text{rang } n &\text{ terme } u_n &\text{ terme }v_n \\ \hline 2& 0 &1 &1\\ \hline 3& 1 &5 &3\\ \hline 4& 2 &19 &13\\ \hline 5& 3 &77 &51\\ \hline 6& 4 &307 &205\\ \hline \end{array} $$
- Quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir par copie vers le bas les termes des suites ? En B3 a pu saisir $=2*B2+3*C2$
- Soit $n$ un entier naturel. Conjecturer la valeur de PGCD$\left(u_n~;~v_n\right)$. Aucune justification n'est demandée. PGCD$(1;1)=1$, PGCD$(5;3)=1$, PGCD$(19,13)=1$.
- Pour les termes de rang 10, 11, 12 et 13 Flore obtient les résultats suivants : $$\begin{array}{|c|c|c|c|}\hline 12 &10 & 1258291 &838861\\ \hline 13 &Il &5033165 &3355443\\ \hline 14 &12 &20132659 &13421773\\ \hline 15 &13 &80530637 &53687091\\ \hline \end{array}$$ Elle émet la conjecture : « la suite $\left(\dfrac{u_n}{v_n} \right)$ converge ». Qu'en penser ? $\dfrac{u_{10}}{v_{10}}\approx 1,499~999~4$
En C3 on a pu saisir $=2*B2+C2$
$\quad$
Il semblerait donc que PGCD$\left(u_n;v_n\right)=1$ pour tout entier naturel $n$.
$\quad$
$\dfrac{u_{11}}{v_{11}}\approx 1,500~000~15$
$\dfrac{u_{12}}{v_{12}}\approx 1,499~999~96$
$\dfrac{u_{13}}{v_{13}}\approx 1,500~000~01$
Il semblerait donc que la suite $\left(\dfrac{u_n}{v_n}\right)$ converge vers $1,5$.
Partie B : Étude arithmétique
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $2u_n - 3v_n = (- 1)^{n+1}$. Initialisation : Si $n=0$ alors $2u_0-3v_0=2-3=-1=(-1)^{0+1}$
- Soit $n$ un entier naturel. Déduire de la question précédente la valeur de PGCD$\left(u_n~;~v_n\right)$. Si $n$ est impair alors $u_n-3v_n=(-1)^{n+1}=1$
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $2u_n-3v_n=(-1)^{n+1}$
$\begin{align*} 2u_{n+1}-3v_{n+1}&=2\left(2u_n+3v_n\right)-3\left(2u_n+v_n\right) \\
&=4u_n+6v_n-6u_n-3v_n \\
&=-2u_n+3v_n \\
&=-\left(2u_n-3v_n\right)\\
&=-(-1)^{n+1}\\
&=(-1)^{n+2}
\end{align*}$
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Pour tout entier naturel $n$ on a donc $2u_n-3v_n=(-1)^{n+1}$.
$\quad$
D’après le théorème de Bezout on a PGCD$\left(u_n;v_n\right)=1$
Si $n$ est pair alors $-\left(u_n-3v_n\right)=-(-1)^{n+1}=1$
Donc $3v_n-2u_n=1$
D’après le théorème de Bezout on a PGCD$\left(u_n;v_n\right)=1$
Dans tous les cas on a PGCD$\left(u_n;v_n\right)=1$.
$\quad$
Partie C : Étude matricielle
Pour tout entier naturel $n$, on définit :
- la matrice colonne $X_n = \begin{pmatrix}u_n\\ v_n\end{pmatrix}$,
- les matrices carrées $P = \begin{pmatrix} 1&3\\- 1&2\end{pmatrix}$ et $Q_n = \begin{pmatrix}(- 1)^n&3 \times 2^{2n}\\(- 1)^{n+1}&2^{2n+1}\end{pmatrix}.$
-
- Montrer que la matrice $\dfrac{1}{5}\begin{pmatrix}2&- 3\\1&1\end{pmatrix}$ est l'inverse de $P$. $\begin{align*} \begin{pmatrix}2&-3\\1&1\end{pmatrix}\times P&=\begin{pmatrix} 2+3&6-6\\1-1&3+2\end{pmatrix} \\
- On admet que, pour tout entier naturel $n$, on a $X_n = Q_nP^{-1} X_0$. Démontrer que, pour tout entier naturel $n$, on a $\left\{\begin{array}{l c l} u_n&=&\dfrac{(- 1)^{n+1}+ 3\times 2^{2n+1}}{5}\\ v_n&=&\dfrac{(- 1)^{n}+ 2^{2n+2}}{5} \end{array}\right.$
&=\begin{pmatrix}5&0\\0&5\end{pmatrix}
\end{align*}$
Par conséquent $\dfrac{1}{5}\begin{pmatrix}2&-3\\1&1\end{pmatrix}\times P=\begin{pmatrix}1&0\\0&1\end{pmatrix}$
La matrice $\dfrac{1}{5}\begin{pmatrix}2&-3\\1&1\end{pmatrix}$ est donc l’inverse de $P$.
$\quad$
$\begin{align*} X_n&=Q_nP^{-1}X_0 \\
&=Q_n\times \dfrac{1}{5}\begin{pmatrix}2&-3\\1&1\end{pmatrix} \times \begin{pmatrix}1\\1\end{pmatrix} \\
&=\dfrac{1}{5}\times Q_n\times \begin{pmatrix}-1\\2\end{pmatrix}\\
&=\dfrac{1}{5}\begin{pmatrix}(-1)^{n+1}+3\times 2^{n+1}\\(-1)^n+2^{2n+2}\end{pmatrix}
\end{align*}$
Par conséquent $\begin{cases}u_n=\dfrac{(-1)^{n+1}+3\times 2^{2n+1}}{5}\\\\v_n=\dfrac{(-1)^n+2^{2n+2}}{5}\end{cases}$
$\quad$ -
- Vérifier que, pour tout entier naturel $n$, on a $\dfrac{u_n}{v_n}= \dfrac{\frac{(- 1)^{n+1}}{2^{2n+1}}+ 3}{\frac{(- 1)^{n}}{2^{2n+1}}+ 2}$. $\begin{align*} \dfrac{u_n}{v_n}&=\dfrac{\dfrac{(-1)^{n+1}+3\times 2^{2n+1}}{5}}{\dfrac{(-1)^n+2^{2n+2}}{5}} \\
- En déduire la limite de la suite $\left(\dfrac{u_n}{v_n} \right)$. $\dfrac{(-1)^{n+1}}{2^{2n+1}}=\dfrac{-1}{2}\times \dfrac{(-1)^{n}}{4^n}=-\dfrac{1}{2}\left(-\dfrac{1}{4}\right)^n$
&=\dfrac{(-1)^{n+1}+3\times 2^{2n+1}}{(-1)^n+2^{2n+2}} \\
&=\dfrac{\dfrac{(-1)^{n+1}}{2^{2n+1}+3}}{\dfrac{(-1)^n}{2^{2n+1}+2}}
\end{align*}$
$\quad$
$\dfrac{(-1)^{n}}{2^{2n+1}}=\dfrac{1}{2}\times \dfrac{(-1)^{n}}{4^n}=\dfrac{1}{2}\left(-\dfrac{1}{4}\right)^n$
Or $-1<-\dfrac{1}{4}<1$ donc $\lim\limits_{n \to +\infty}\left(-\dfrac{1}{4}\right)^n=0$
Donc $\lim\limits_{n \to +\infty}\dfrac{u_n}{v_n}=\dfrac{3}{2}$.
$\quad$
Géométrie 3 points
On considère un cube ABCDEFGH fourni en annexe. L'espace est rapporté au repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$. On note $\mathcal{P}$ le plan d'équation $x + \dfrac{1}{2} y +\dfrac{1}{3}z -1 = 0$. Construire, sur la figure fournie en annexe, la section du cube par le plan $\mathcal{P}$. La construction devra être justifiée par des calculs ou des arguments géométriques. 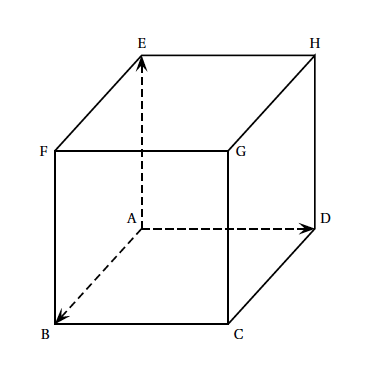
Géométrie 3 points
On recherche trois points du cube appartenant au plan $\mathscr{P}$.
Les points $B(1;0;0)$, $I\left(\dfrac{1}{2};1;0\right)$ et $J\left(\dfrac{2}{3};0;1\right)$ appartiennent au plan $\mathscr{P}$ d’équation $x+\dfrac{1}{2}x+\dfrac{1}{3}z-1=0$.
En effet :
- $1+0+0-1=0$ (point $B)$
- $\dfrac{1}{2}+\dfrac{1}{2}+0-1=0$ (point $I$)
- $\dfrac{2}{3}+0+\dfrac{1}{3}-1=0$ (point $J$)
Les plan $\mathscr{P}$ et $(BIJ)$ sont donc confondus.
Les plans $(ABC)$ et $(EFG)$ sont parallèles. Par conséquent, l’intersection du plan $(EFG)$ avec le plan $(BIJ)$ est la droite parallèle à $(BI)$ passant par $J$. Le point $L$ est le point d’intersection de cette droite avec l’arête $[GH]$.
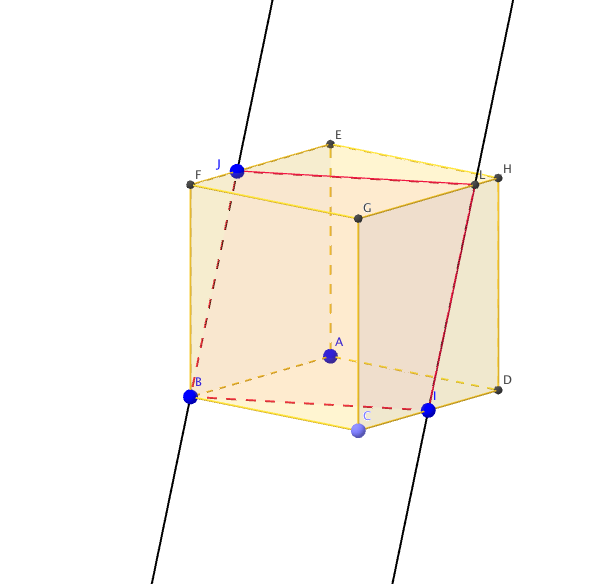
- Vues: 21227
