Baccalauréat S Pondichéry 26 Avril 2017 - Correction Exercice 3

Page 6 sur 12: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Une entreprise spécialisée dans les travaux de construction a été mandatée pour percer un tunnel à flanc de montagne. Après étude géologique, l'entreprise représente dans le plan la situation de la façon suivante : dans un repère orthonormal, d'unité 2 m, la zone de creusement est la surface délimitée par l'axe des abscisses et la courbe $\mathcal{C}$.
 
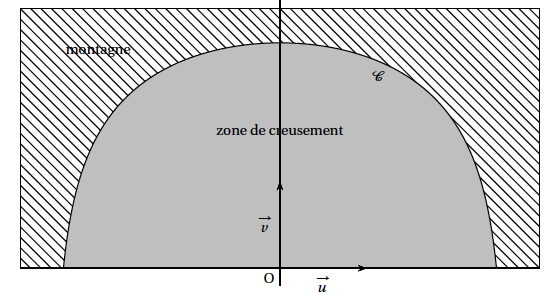
On admet que $\mathcal{C}$ est la courbe représentative de la fonction $f$ définie sur l'intervalle $[- 2,5~;~2,5]$ par: \[f(x) = \ln \left(- 2x^2 + 13,5\right).\] L'objectif est de déterminer une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.

Partie A : Étude de la fonction $f$

 

1. Calculer $f ‘(x)$ pour $x \in [- 2,5~;~2,5]$.
On appelle $u$ la fonction définie sur $[-2,5;2,5]$ par $u(x)=-2x^2+13,5$.
La fonction $u$ est dérivable sur cet intervalle en tant que polynôme et, de par la définition de la fonction $f$, est également strictement positive sur cet intervalle.
Par composition des fonctions, la fonction $f$ est dérivable sur l’intervalle $[-2,5;2,5]$
$f(x)=\ln\left(u(x)\right)$ donc $f'(x)=\dfrac{u'(x)}{u(x)}$.
$f'(x)=\dfrac{-4x}{-2x^2+13,5}$
$\quad$
2. Dresser, en justifiant, le tableau de variation de la fonction $f$ sur $[- 2,5~;~2,5]$. En déduire le signe de $f$ sur $[- 2,5~;~2,5]$.
Puisque $-2x^2+13,5>0$ sur l’intervalle $[2,5;2,5]$ le signe de $f'(x)$ ne dépend que de celui de $-4x$.
Ainsi $f'(x)>0$ sur l’intervalle $[-2,5;0]$ et $f'(x)>0$ sur l’intervalle $[0;2,5]$.
On obtient alors le tableau de variation suivant :

 

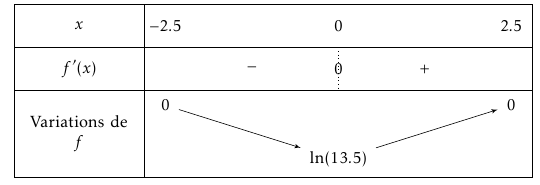
Partie B : Aire de la zone de creusement

On admet que la courbe $\mathcal{C}$ est symétrique par rapport à l'axe des ordonnées du repère.

1. La courbe $\mathcal{C}$ est-elle un arc de cercle de centre 0 ? Justifier la réponse.
La hauteur du tunnel est $h=\ln(13,5)\approx 2,6$.
La largeur du tunnel est $\ell = 2,5\times 2=5 \neq 2h$.
La courbe $\mathscr{C}$ n’est donc pas un arc de cercle de centre $O$.
$\quad$
2. Justifier que l'aire, en mètre carré, de la zone de creusement est $\mathcal{A} = 8\displaystyle\int_0^{2,5} f(x)\:\text{d}x$.
Par symétrie $\mathscr{A}$ est le double de l’aire comprise entre la courbe $\mathscr{C}$, l’axe des abscisses, la droite d’équation $x=0$ et celle d’équation $x=2,5$.
Donc :
$\begin{align*} \mathscr{A}&=\displaystyle 2\int_0^{2,5}f(x)\text{d}x~~ \text{u.a.} \\
&=2\int_0^{2,5}f(x)\text{d}x\times 2^2 \text{ m}^2 \\
&=8\int_0^{2,5}f(x)\text{d}x\text{ m}^2
\end{align*}$
$\quad$
3. L'algorithme, donné en annexe, permet de calculer une valeur approchée par défaut de $I = \displaystyle\int_0^{2,5} f(x)\:\text{d}x$, notée $a$. On admet que : $a \leqslant I \leqslant a + \dfrac{f(0) - f(2,5)}{n}\times 2,5$.
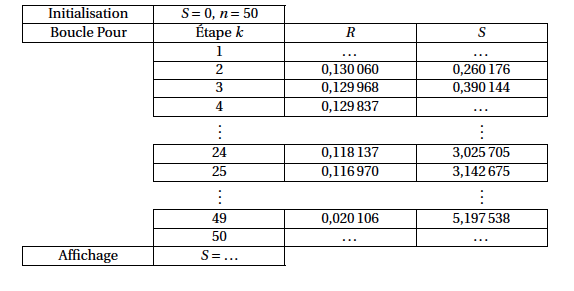
   1. Le tableau fourni en annexe, donne différentes valeurs obtenues pour R et S lors de l'exécution de l'algorithme pour $n = 50$. Compléter ce tableau en calculant les six valeurs manquantes.
   A l’étape $1$ on a $R=0,130~116$ et $S=0,130~116$
   A l’étape $4$ on a $S=0,519~981$
   A l’étape $50$ on a $R=0$ et $S=5,197~538$
   A l’affichage $S=5,197~538$
   $\quad$
   
   2. En déduire une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
   Une valeur approchée de $\displaystyle \int_0^{2,5} f(x)\text{d}x$ est $5,197~538$.
   Par conséquent une valeur approchée de la zone de creusement est :
   $\mathscr{A}\approx 8\times 5,197~538$
   Soit $\mathscr{A} \approx 41,580~304 \approx 42$ m$^2$.
   $\quad$

 

$$\begin{array}{|l|}\hline \text{Variables}\\ \hspace{1cm}\begin{array}{|l} R \text{ et } S \text{ sont des réels}\\ n \text{ et }k \text{ sont des entiers}\\ \end{array}\\ \text{Traitement} \\ \hspace{1cm}\begin{array}{|l} S \text{ prend la valeur } 0\\ \text{ Demander la valeur de } n\\ \text{Pour } k \text{ variant de } 1 \text{ à } n \text{ faire }\\ \hspace{1cm}\begin{array}{|l} R \text{ prend la valeur } \dfrac{2,5}{n} \times f\left(\dfrac{2,5}{n}\times k \right)\\ S \text{ prend la valeur } S + R\\ \end{array}\\ \text{ Fin Pour}\\ \text{ Afficher } S\\ \end{array}\\ \hline \end{array}$$ Le tableau ci-dessous donne les valeurs de $R$ et de $S$, arrondies à $10^{-6}$, obtenues lors de l'exécution de l'algorithme pour $n = 50$.