Baccalauréat S Antilles Guyane16 juin 2017
Exercice 1 3 points
On munit le plan complexe d'un repère orthonormé direct. On considère l'équation \[(E) :\qquad z^4 + 2z^3 - z - 2 = 0\] ayant pour inconnue le nombre complexe $z$.
- Donner une solution entière de $(E)$.
- Démontrer que, pour tout nombre complexe $z$, \[z^4 + 2z^3 - z - 2 = \left(z^2 + z - 2\right)\left(z^2 + z + 1\right).\]
- Résoudre l'équation $(E)$ dans l'ensemble des nombres complexes.
- Les solutions de l'équation $(E)$ sont les affixes de quatre points A, B, C, D du plan complexe tels que ABCD est un quadrilatère non croisé. Le quadrilatère ABCD est-il un losange ? Justifier.
Correction de l'exercice 1 (3 points)
On munit le plan complexe d'un repère orthonormé direct. On considère l'équation \[(E) :\qquad z^4 + 2z^3 - z - 2 = 0\] ayant pour inconnue le nombre complexe $z$.
- Donner une solution entière de $(E)$.
- Démontrer que, pour tout nombre complexe $z$, \[z^4 + 2z^3 - z - 2 = \left(z^2 + z - 2\right)\left(z^2 + z + 1\right).\]
- Résoudre l'équation $(E)$ dans l'ensemble des nombres complexes.
- Les solutions de l'équation $(E)$ sont les affixes de quatre points A, B, C, D du plan complexe tels que ABCD est un quadrilatère non croisé. Le quadrilatère ABCD est-il un losange ? Justifier.
Exercice 2 5 points
Dans une usine automobile, certaines pièces métalliques sont recouvertes d'une fine couche de nickel qui les protège contre la corrosion et l'usure. Le procédé utilisé est un nickelage par électrolyse.
On admet que la variable aléatoire $X$, qui à chaque pièce traitée associe l'épaisseur de nickel déposé, suit la loi normale d'espérance $\mu_1 = 25$ micromètres ($\mu$m) et d'écart type $\sigma_1$.
Une pièce est conforme si l'épaisseur de nickel déposé est comprise entre 22,8 µm et 27,2 µm.
La fonction de densité de probabilité de $X$ est représentée ci-dessous. On a pu déterminer que $P(X > 27,2) = 0,023$. 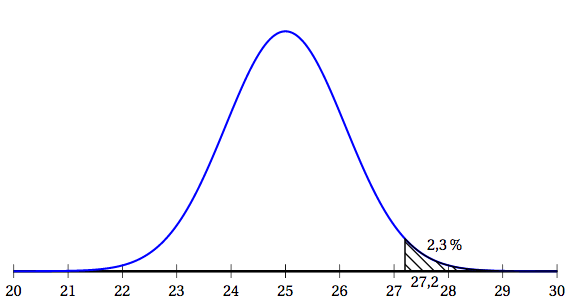
-
- Déterminer la probabilité qu'une pièce soit conforme.
- Justifier que 1,1 est une valeur approchée de $\sigma_1$ à $10^{-1}$ près.
- Sachant qu'une pièce est conforme, calculer la probabilité que l'épaisseur de nickel déposé sur celle-ci soit inférieure à $24~\mu$m. Arrondir à $10^{-3}$.
- Une équipe d'ingénieurs propose un autre procédé de nickelage, obtenu par réaction chimique sans aucune source de courant. L'équipe affirme que ce nouveau procédé permet théoriquement d'obtenir 98 % de pièces conformes. La variable aléatoire $Y$ qui, à chaque pièce traitée avec ce nouveau procédé, associe l'épaisseur de nickel déposé suit la loi normale d'espérance $\mu_2 = 25 ~\mu$m et d'écart-type $\sigma_2$.
- En admettant l'affirmation ci-dessus, comparer $\sigma_1$ et $\sigma_2$.
- Un contrôle qualité évalue le nouveau procédé; il révèle que sur 500 pièces testées, $15$ ne sont pas conformes. Au seuil de 95 %, peut-on rejeter l'affirmation de l'équipe d'ingénieurs ?
Correction de l'exercice 2 (5 points)
Exercice 3 5 points
Soient $f$ et $g$ les fonctions définies sur l'ensemble $\mathbb R$ des nombres réels par \[f(x) = \text{e}^x\qquad \text{ et }\qquad g(x) = \text{e}^{- x}.\] On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ et $\mathcal{C}_g$ celle de la fonction $g$ dans un repère orthonormé du plan. Pour tout réel $a$, on note $M$ le point de $\mathcal{C}_f$ d'abscisse $a$ et $N$ le point de $\mathcal{C}_g$ d'abscisse $a$. La tangente en $M$ à $\mathcal{C}_f$ coupe l'axe des abscisses en $P$, la tangente en $N$ à $\mathcal{C}_g$ coupe l'axe des abscisses en $Q$. À l'aide d'un logiciel de géométrie dynamique, on a représenté la situation pour différentes valeurs de $a$ et on a relevé dans un tableur la longueur du segment $[PQ]$ pour chacune de ces valeurs de $a$.
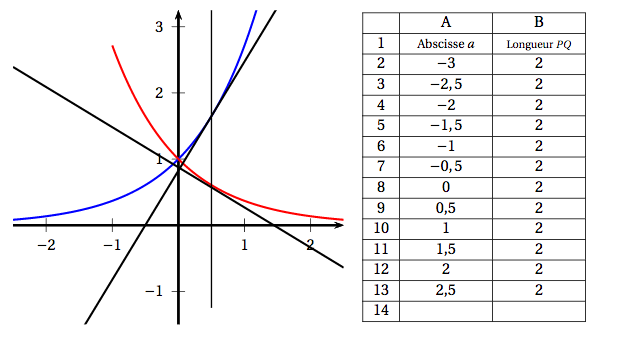
Les questions 1 et 2 peuvent être traitées de manière indépendante.
- Démontrer que la tangente en $M$ à $\mathcal{C}_f$ est perpendiculaire à la tangente en $N$ à $\mathcal{C}_g$.
-
- Que peut-on conjecturer pour la longueur $PQ$ ?
- Démontrer cette conjecture.
Correction de l'exercice 3 (5 points)
Exercice 4 5 points
Correction de l'exercice 4 5 points
Spécialité 5 points
Correction de l'exercice de Spécialité 5 points
- Vues: 32089
