Baccalauréat S Métropole 22 juin 2018
Exercice 1 6 points
Dans cet exercice, on munit le plan d'un repère orthonormé.
On a représenté ci-dessous la courbe d'équation: \[y = \dfrac{1}{2}\left(\text{e}^x + \text{e}^{-x} - 2\right).\] Cette courbe est appelée une « chaînette ». On s'intéresse ici aux « arcs de chaînette» délimités par deux points de cette courbe symétriques par rapport à l'axe des ordonnées. Un tel arc est représenté sur le graphique ci-dessous en trait plein. On définit la « largeur » et la « hauteur » de l'arc de chaînette délimité par les points $M$ et $M'$ comme indiqué sur le graphique. 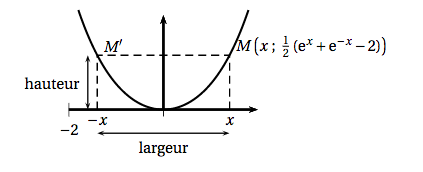
Le but de l'exercice est d'étudier les positions possibles sur la courbe du point $M$ d'abscisse $x$ strictement positive afin que la largeur de l'arc de chaînette soit égale à sa hauteur.
- Justifier que le problème étudié se ramène à la recherche des solutions strictement positives de l'équation \[(E) : \text{e}^x + \text{e}^{- x} - 2 = 0.\]
- On note $f$ la fonction définie sur l'intervalle $[0~;~ +\infty[$ par : \[f(x) = \text{e}^x + \text{e}^{- x} - 4x - 2.\]
- Vérifier que pour tout $x > 0,\: f(x) = x \left(\dfrac{\text{e}^x}{x}- 4\right) + \text{e}^{- x} - 2$.
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$.
-
- On note $f'$ la fonction dérivée de la fonction $f$. Calculer $f'(x)$, où $x$ appartient à l'intervalle $[0~;~ +\infty[$.
- Montrer que l'équation $f'(x) = 0$ équivaut à l'équation : $\left(\text{e}^x\right)^2 - 4\text{e}^x - 1 = 0$.
- En posant $X = \text{e}^x$, montrer que l'équation $f'(x) = 0$ admet pour unique solution réelle le nombre $\ln \left(2 + \sqrt{5}\right)$.
- On donne ci-dessous le tableau de signes de la fonction dérivée $f'$ de $f$ :
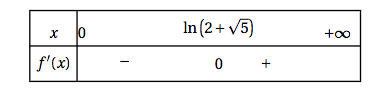
- Dresser le tableau de variations de la fonction $f$.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution strictement positive que l'on notera $\alpha$.
- On considère l'algorithme suivant où les variables $a$, $b$ et $m$ sont des nombres réels : $$\begin{array}{|l|}\hline \text{Tant que } b - a > 0,1 \text{faire:}\\ \hspace{1cm} m \gets \dfrac{a+b}{2} \\ \hspace{1cm}\text{ Si } \text{e}^m + \text{e}^{-m} - 4m - 2 > 0 \text{, alors:}\\ \hspace{2cm} b \gets m \\ \hspace{1cm}\text{Sinon :}\\ \hspace{2cm} a\gets m \\ \hspace{1cm}\text{Fin Si }\\ \text{Fin Tant que }\\ \hline \end{array}$$
- Avant l'exécution de cet algorithme, les variables $a$ et $b$ contiennent respectivement les valeurs $2$ et $3$. Que contiennent-elles à la fin de l'exécution de l'algorithme ? On justifiera la réponse en reproduisant et en complétant le tableau ci-contre avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme.
- Comment peut-on utiliser les valeurs obtenues en fin d'algorithme à la question précédente ?
- La Gateway Arch, édifiée dans la ville de Saint-Louis aux États-Unis, a l'allure ci-contre. Son profil peut être approché par un arc de chaînette renversé dont la largeur est égale à la hauteur.
La largeur de cet arc, exprimée en mètre, est égale au double de la solution strictement positive de l'équation : \[\left(E'\right) : \text{e}^{\frac{t}{39}} + \text{e}^{-\frac{t}{39}} - 4\frac{t}{39} - 2 = 0.\] Donner un encadrement de la hauteur de la Gateway Arch.
Correction de l'exercice 1 (6 points)
Dans cet exercice, on munit le plan d'un repère orthonormé.
On a représenté ci-dessous la courbe d'équation: \[y = \dfrac{1}{2}\left(\text{e}^x + \text{e}^{-x} - 2\right).\] Cette courbe est appelée une « chaînette ». On s'intéresse ici aux « arcs de chaînette» délimités par deux points de cette courbe symétriques par rapport à l'axe des ordonnées. Un tel arc est représenté sur le graphique ci-dessous en trait plein. On définit la « largeur » et la « hauteur » de l'arc de chaînette délimité par les points $M$ et $M'$ comme indiqué sur le graphique. 
Le but de l'exercice est d'étudier les positions possibles sur la courbe du point $M$ d'abscisse $x$ strictement positive afin que la largeur de l'arc de chaînette soit égale à sa hauteur.
- Justifier que le problème étudié se ramène à la recherche des solutions strictement positives de l'équation \[(E) : \text{e}^x + \text{e}^{- x} - 2 = 0.\] La largeur de la chaînette est $MM’=2x$.
- On note $f$ la fonction définie sur l'intervalle $[0~;~ +\infty[$ par : \[f(x) = \text{e}^x + \text{e}^{- x} - 4x - 2.\]
- Vérifier que pour tout $x > 0,\: f(x) = x \left(\dfrac{\text{e}^x}{x}- 4\right) + \text{e}^{- x} - 2$. $x\left(\dfrac{\text{e}^x}{x}-4\right)+\text{e}^{-x}-2 =\text{e}^x-4x+\text{e}^{-x}-2=f(x)$.
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$. $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$
$\quad$
Donc $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$.
De plus $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} x\left(\dfrac{\text{e}^x}{x}-4\right)=+\infty$.
Par conséquent $\lim\limits_{x \to +\infty} f(x)=+\infty$.
$\quad$ -
- On note $f'$ la fonction dérivée de la fonction $f$. Calculer $f'(x)$, où $x$ appartient à l'intervalle $[0~;~ +\infty[$. La fonction $f$ est dérivable sur l’intervalle $[0;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
- Montrer que l'équation $f'(x) = 0$ équivaut à l'équation : $\left(\text{e}^x\right)^2 - 4\text{e}^x - 1 = 0$. $\begin{align*} f'(x)=0 &\iff \text{e}^x-\text{e}^{-x}-4=0 \\
- En posant $X = \text{e}^x$, montrer que l'équation $f'(x) = 0$ admet pour unique solution réelle le nombre $\ln \left(2 + \sqrt{5}\right)$. On pose $X=\text{e}^x$.
$f'(x)=\text{e}^x-\text{e}^{-x}-4$.
$\quad$
&\iff \dfrac{\text{e}{2x}-1-4\text{e}^x}{\text{e}^x}=0 \\
&\iff \dfrac{\left(\text{e}^x\right)^2-4\text{e}^x-1}{\text{e}^x}=0
&\iff \left(\text{e}^x\right)^2-4\text{e}^x-1=0 \quad \text{car } \text{e}^x >0 \text{ sur } [0;+\infty[
\end{align*}$
$\quad$
On a alors
$ \left(\text{e}^x\right)^2-4\text{e}^x-1=0 \iff \begin{cases} X=\text{e}^x\\X^2-4X-1=0 \end{cases} $
Calculons le discriminant du polynôme $X^2-4X-1$
$\Delta = (-4)^2-4\times 1\times (-1)=20>0$
Il possède donc deux racines réelles : $X_1=\dfrac{4-\sqrt{20}}{2}=2-\sqrt{5} <0$
et $X_2=\dfrac{4+\sqrt{20}}{2}=2+\sqrt{5}>0$.
Ainsi :
$\begin{cases} X=\text{e}^x\\X^2-4X-1=0 \end{cases} \iff \begin{cases} X=\text{e}^x \\X=2-\sqrt{5} \text{ou } X=2+\sqrt{5}\end{cases}$
$X_1<0$ donc la seule solution possible est celle qui vérifie $2+\sqrt{5}=\text{e}^x \iff x=\ln \left(2+\sqrt{5}\right)$.
$\quad$ - On donne ci-dessous le tableau de signes de la fonction dérivée $f'$ de $f$ :
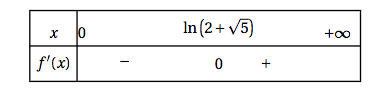
- Dresser le tableau de variations de la fonction $f$. On obtient le tableau de variation suivant :
- Démontrer que l'équation $f(x) = 0$ admet une unique solution strictement positive que l'on notera $\alpha$. $f$ est strictement décroissante sur l'intervalle $\left]0; \ln \left(2+\sqrt{5}\right)\right[$;
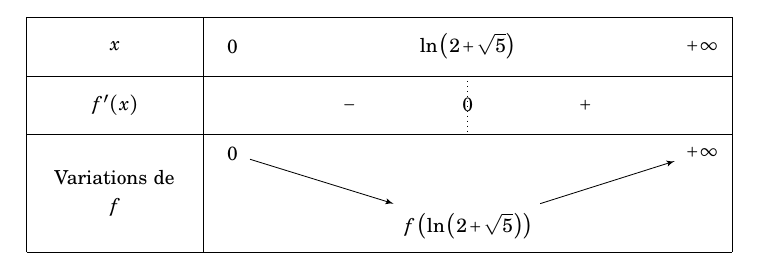
On a $f\left(\ln \left(2+\sqrt{5}\right)\right) \approx -3,3$.
$\quad$
donc si $0<x<\ln \left(2+\sqrt{5}\right)$ alors $0> f(x)$, soit $f(x)< 0$.
Sur l’intervalle $\left]0;\ln \left(2+\sqrt{5}\right)\right[$ on a $f(x)<0$.
Sur l’intervalle $\left[\ln \left(2+\sqrt{5}\right);+\infty\right[$, la fonction $f$ est continue (car dérivable) et strictement croissante.
De plus $f\left(\ln \left(2+\sqrt{5}\right)\right) \approx -3,3<0$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=0$ possède une unique solution $\alpha$ sur l’intervalle $\left[\ln \left(2+\sqrt{5}\right);+\infty\right[$.
Ainsi l’équation $f(x)=0$ possède une unique solution sur l’intervalle $[0;+\infty[$.
$\quad$ - On considère l'algorithme suivant où les variables $a$, $b$ et $m$ sont des nombres réels : $$\begin{array}{|l|}\hline \text{Tant que } b - a > 0,1 \text{faire:}\\ \hspace{1cm} m \gets \dfrac{a+b}{2} \\ \hspace{1cm}\text{ Si } \text{e}^m + \text{e}^{-m} - 4m - 2 > 0 \text{, alors:}\\ \hspace{2cm} b \gets m \\ \hspace{1cm}\text{Sinon :}\\ \hspace{2cm} a\gets m \\ \hspace{1cm}\text{Fin Si }\\ \text{Fin Tant que }\\ \hline \end{array}$$
- Avant l'exécution de cet algorithme, les variables $a$ et $b$ contiennent respectivement les valeurs $2$ et $3$. Que contiennent-elles à la fin de l'exécution de l'algorithme ? On justifiera la réponse en reproduisant et en complétant le tableau ci-contre avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme. $$ \begin{array}{|c|c|c|c|}\hline m & a & b & b - a \\ \hline &2& 3 &1\\ \hline 2,5 &&&\\ \hline \ldots &\ldots&\ldots&\\ \hline ~ &&&\\ \hline \end{array}$$ $$\begin{array}{|c|c|c|c|}
- Comment peut-on utiliser les valeurs obtenues en fin d'algorithme à la question précédente ? On a $f(2)\approx -2,48$ et $f(3)\approx 6,14$.
\hline
m&a&b&b-a\\
\hline
&2&3&1\\
\hline
2,5&2&2,5&0,5\\
\hline
2,25&2,25&2,5&0,25\\
\hline
2,375&2,375&2,5&0,125\\
\hline
2,4375&2,4375&2,5&0,0625\\
\hline
\end{array}$$
À la fin de l’exécution de l’algorithme on a $a=2,437~5$ et $b=2,5$.
$\quad$
Par conséquent $\alpha$ appartient à l’intervalle $]2;3[$.
L’algorithme (de dichotomie) précédent nous fournit un encadrement d’amplitude au plus $0,1$ de cette valeur.
Donc $2,437~5 <\alpha < 2,5$.
$\quad$ - La Gateway Arch, édifiée dans la ville de Saint-Louis aux États-Unis, a l'allure ci-contre. Son profil peut être approché par un arc de chaînette renversé dont la largeur est égale à la hauteur.

La largeur de cet arc, exprimée en mètre, est égale au double de la solution strictement positive de l'équation : \[\left(E'\right) : \text{e}^{\frac{t}{39}} + \text{e}^{-\frac{t}{39}} - 4\frac{t}{39} - 2 = 0.\] Donner un encadrement de la hauteur de la Gateway Arch. D’après la question précédente la solution de l’équation $(E’)$ vérifie :
La hauteur de la chaînette est $\dfrac{1}{2}\left(\text{e}^x+\text{e}^{-x}-2\right)$.
On veut donc résoudre :
$\begin{align*} 2x=\dfrac{1}{2}\left(\text{e}^x+\text{e}^{-x}-2\right)&\iff 4x=\text{e}^x+\text{e}^{-x}-2 \\
&\iff \text{e}^x+\text{e}^{-x}-4x-2 = 0\end{align*}$
$\quad$
$2,437~5< \dfrac{t}{39}<2,5 \iff 95,062~5<t<97,5$.
Un encadrement de la largeur de cet arc est donc $190,125<2t<195$.
$\quad$ donc la hauteur de l'arche est comprise entre 190 et 195 mètres.
Exercice 2 4 points
Les parties A et B de cet exercice sont indépendantes.
Le virus de la grippe atteint chaque année, en période hivernale, une partie de la population d'une ville. La vaccination contre la grippe est possible; elle doit être renouvelée chaque année.
Partie A
L'efficacité du vaccin contre la grippe peut être diminuée en fonction des caractéristiques individuelles des personnes vaccinées, ou en raison du vaccin, qui n'est pas toujours totalement adapté aux souches du virus qui circulent. Il est donc possible de contracter la grippe tout en étant vacciné. Une étude menée dans la population de la ville à l'issue de la période hivernale a permis de constater que :
- 40 % de la population est vaccinée ;
- 8 % des personnes vaccinées ont contracté la grippe ;
- 20 % de la population a contracté la grippe.
On choisit une personne au hasard dans la population de la ville et on considère les évènements :
- $V$ : « la personne est vaccinée contre la grippe » ;
- $G$ : « la personne a contracté la grippe ».
-
- Donner la probabilité de l'évènement $G$.
- Reproduire l'arbre pondéré ci-dessous et compléter les pointillés indiqués sur quatre de ses branches.
- Déterminer la probabilité que la personne choisie ait contracté la grippe et soit vaccinée.
- La personne choisie n'est pas vaccinée. Montrer que la probabilité qu'elle ait contracté la grippe est égale à $0,28$.
Partie B
Dans cette partie, les probabilités demandées seront données à $10^{-3}$ près.
Un laboratoire pharmaceutique mène une étude sur la vaccination contre la grippe dans cette ville.
Après la période hivernale, on interroge au hasard $n$ habitants de la ville, en admettant que ce choix se ramène à $n$ tirages successifs indépendants et avec remise.
On suppose que la probabilité qu'une personne choisie au hasard dans la ville soit vaccinée contre la grippe est égale à $0,4$. On note $X$ la variable aléatoire égale au nombre de personnes vaccinées parmi les $n$ interrogées.
- Quelle est la loi de probabilité suivie par la variable aléatoire $X$ ?
- Dans cette question, on suppose que $n = 40$.
- Déterminer la probabilité qu'exactement $15$ des $40$ personnes interrogées soient vaccinées.
- Déterminer la probabilité qu'au moins la moitié des personnes interrogées soit vaccinée.
- On interroge un échantillon de $3750$ habitants de la ville, c'est-à-dire que l'on suppose ici que $n =3 750$. On note $Z$ la variable aléatoire définie par : $Z = \dfrac{X - 1 500 }{30}$.
On admet que la loi de probabilité de la variable aléatoire $Z$ peut être approchée par la loi normale centrée réduite.
En utilisant cette approximation, déterminer la probabilité qu'il y ait entre $1450$ et $1550$ individus vaccinés dans l'échantillon interrogé.
Correction de l'exercice 2 (4 points)
Les parties A et B de cet exercice sont indépendantes.
Le virus de la grippe atteint chaque année, en période hivernale, une partie de la population d'une ville. La vaccination contre la grippe est possible; elle doit être renouvelée chaque année.Partie A
L'efficacité du vaccin contre la grippe peut être diminuée en fonction des caractéristiques individuelles des personnes vaccinées, ou en raison du vaccin, qui n'est pas toujours totalement adapté aux souches du virus qui circulent. Il est donc possible de contracter la grippe tout en étant vacciné. Une étude menée dans la population de la ville à l'issue de la période hivernale a permis de constater que :- 40 % de la population est vaccinée ;
- 8 % des personnes vaccinées ont contracté la grippe ;
- 20 % de la population a contracté la grippe.
On choisit une personne au hasard dans la population de la ville et on considère les évènements :- $V$ : « la personne est vaccinée contre la grippe » ;
- $G$ : « la personne a contracté la grippe ».
-
- Donner la probabilité de l'évènement $G$. D’après l’énoncé, on a $p(G)=0,2$.
- Reproduire l'arbre pondéré ci-dessous et compléter les pointillés indiqués sur quatre de ses branches.

$\quad$
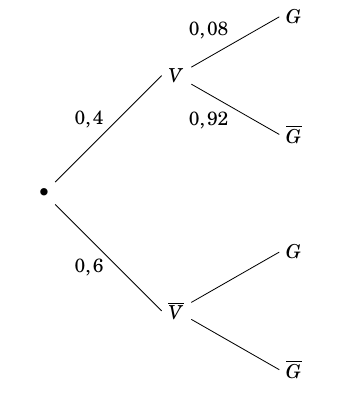
- Déterminer la probabilité que la personne choisie ait contracté la grippe et soit vaccinée. On veut calculer $p(V\cap G)=0,4\times 0,08=0,032$.
- La personne choisie n'est pas vaccinée. Montrer que la probabilité qu'elle ait contracté la grippe est égale à $0,28$. D’après la formule des probabilités totales on a :
$\begin{align*}p(G)=p(V\cap G)+p\left(\overline{V}\cap G\right) &\iff 0,2=0,032+p\left(\overline{V}\cap G\right) \\
&\iff p\left(\overline{V}\cap G\right)=0,168
\end{align*}$
Par conséquent :
$\begin{align*} p_{\overline{V}}(G)&=\dfrac{p\left(\overline{V}\cap G\right)}{p\left(\overline{V}\right)} \\
&=\dfrac{0,168}{0,6} \\
&=0,28
\end{align*}$
$\quad$
Partie B
Dans cette partie, les probabilités demandées seront données à $10^{-3}$ près.
Un laboratoire pharmaceutique mène une étude sur la vaccination contre la grippe dans cette ville.
Après la période hivernale, on interroge au hasard $n$ habitants de la ville, en admettant que ce choix se ramène à $n$ tirages successifs indépendants et avec remise.
On suppose que la probabilité qu'une personne choisie au hasard dans la ville soit vaccinée contre la grippe est égale à $0,4$. On note $X$ la variable aléatoire égale au nombre de personnes vaccinées parmi les $n$ interrogées.
- Quelle est la loi de probabilité suivie par la variable aléatoire $X$ ? On effectue $n$ tirages aléatoires, indépendants et identiques.
- Dans cette question, on suppose que $n = 40$.
- Déterminer la probabilité qu'exactement $15$ des $40$ personnes interrogées soient vaccinées. On a $p(X=15)=\displaystyle \binom{40}{15}\times 0,4^{15}\times 0,6^{40-15} \approx 0,123$.
- Déterminer la probabilité qu'au moins la moitié des personnes interrogées soit vaccinée. On veut calculer $p(X \geq 20)=1-p(X\leq 19) \approx 0,130$
La probabilité qu’exactement $15$ des $40$ personnes interrogées soient vaccinées est d’environ $12,3\%$.
$\quad$
2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
La probabilité qu’au moins la moitié des personnes soit vaccinée est d’environ $13\%$.
$\quad$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$ - On interroge un échantillon de $3750$ habitants de la ville, c'est-à-dire que l'on suppose ici que $n =3 750$. On note $Z$ la variable aléatoire définie par : $Z = \dfrac{X - 1 500 }{30}$.
On admet que la loi de probabilité de la variable aléatoire $Z$ peut être approchée par la loi normale centrée réduite.
En utilisant cette approximation, déterminer la probabilité qu'il y ait entre $1450$ et $1550$ individus vaccinés dans l'échantillon interrogé. $\quad$
Chaque tirage possède deux issues $V$ et $\overline{V}$.
De plus $p(V)=0,4$.
La variable aléatoire $X$ suit donc la loi binomiale de paramètres $n$ et $p=0,4$.
$\begin{align*} p(1~450 \leq X \leq 1~550) & = p(-50 \leq X-1~500 \leq 50) \\
&=p\left(-\dfrac{50}{30} \leq \dfrac{X-1~500}{30} \leq \dfrac{50}{30} \right) \\
&=p\left(-\dfrac{5}{3} \leq Z\leq \dfrac{5}{3}\right) \\
&\approx 0,904
\end{align*}$2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
Exercice 3 5 points
Le but de cet exercice est d'examiner, dans différents cas, si les hauteurs d'un tétraèdre sont concourantes, c'est-à-dire d'étudier l'existence d'un point d'intersection de ses quatre hauteurs. On rappelle que dans un tétraèdre MNPQ, la hauteur issue de M est la droite passant par M orthogonale au plan (NPQ).
Partie A Étude de cas particuliers
On considère un cube ABCDEFGH.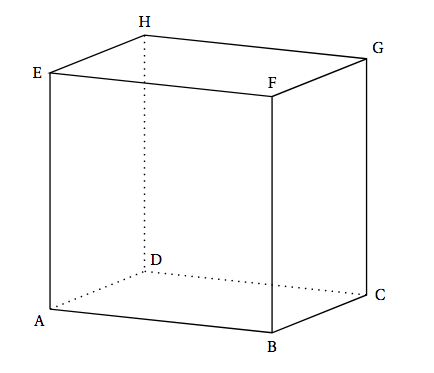
On admet que les droites (AG), (BH), (CE) et (DF), appelées « grandes diagonales» du cube, sont concourantes.
- On considère le tétraèdre ABCE.
- Préciser la hauteur issue de E et la hauteur issue de C dans ce tétraèdre.
- Les quatre hauteurs du tétraèdre ABCE sont-elles concourantes?
- On considère le tétraèdre ACHF et on travaille dans le repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
- Vérifier qu'une équation cartésienne du plan (ACH) est : $x - y + z = 0$.
- En déduire que (FD) est la hauteur issue de F du tétraèdre ACHF.
- Par analogie avec le résultat précédent, préciser les hauteurs du tétraèdre ACHF issues respectivement des sommets A, C et H. Les quatre hauteurs du tétraèdre ACHF sont-elles concourantes ?
Partie B Une propriété des tétraèdres orthocentriques
Dans cette partie, on considère un tétraèdre MNPQ dont les hauteurs issues des sommets M et N sont sécantes en un point K. Les droites (MK) et (NK) sont donc orthogonales aux plans (NPQ) et (MPQ) respectivement.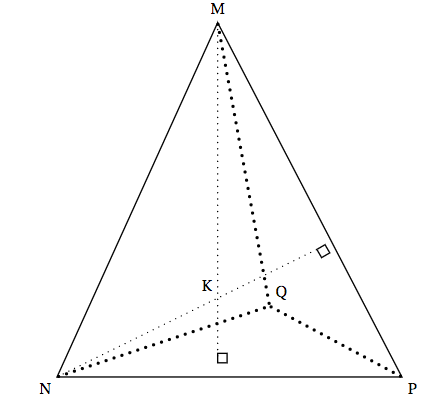
-
- Justifier que la droite (PQ) est orthogonale à la droite (MK) ; on admet de même que les droites (PQ) et (NK) sont orthogonales.
- Que peut-on déduire de la question précédente relativement à la droite (PQ) et au plan (MNK) ? Justifier la réponse.
- Montrer que les arêtes [MN] et [PQ] sont orthogonales. Ainsi, on obtient la propriété suivante : Si un tétraèdre est orthocentrique, alors ses arêtes opposées sont orthogonales deux à deux.
(On dit que deux arêtes d'un tétraèdre sont « opposées» lorsqu'elles n'ont pas de sommet commun.)
Partie C Application
Dans un repère orthonormé, on considère les points : \[\text{R}(-3~;~5~;~2) ,\text{S}(1~;~4~;~-2) , \text{T}(4~;~-1~;~5)\quad \text{et U}(4~;~7~;~3).\] Le tétraèdre RSTU est-il orthocentrique ? Justifier.
Correction de l'exercice 3 (5 points)
Le but de cet exercice est d'examiner, dans différents cas, si les hauteurs d'un tétraèdre sont concourantes, c'est-à-dire d'étudier l'existence d'un point d'intersection de ses quatre hauteurs. On rappelle que dans un tétraèdre MNPQ, la hauteur issue de M est la droite passant par M orthogonale au plan (NPQ).
Partie A Étude de cas particuliers
On considère un cube ABCDEFGH.
On admet que les droites (AG), (BH), (CE) et (DF), appelées « grandes diagonales» du cube, sont concourantes.
- On considère le tétraèdre ABCE.
- Préciser la hauteur issue de E et la hauteur issue de C dans ce tétraèdre. Dans le tétraèdre $ABCE$, la hauteur issue de $E$ est $[EA]$car $(EA) \perp (ABC)$ et celle issue de $C$ est $[BC]$ car $(CB) \perp (ABE)$ .
- Les quatre hauteurs du tétraèdre ABCE sont-elles concourantes? Les droites $(EA)$ et $(BC)$ ne sont pas coplanaires. Les quatre hauteurs du tétraèdre $ABCE$ ne sont donc pas concourantes.
$\quad$
- On considère le tétraèdre ACHF et on travaille dans le repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
- Vérifier qu'une équation cartésienne du plan (ACH) est : $x - y + z = 0$. Dans le repère $\left(A;\vec{AB},\vec{AD},\vec{AE}\right)$ on a :
- En déduire que (FD) est la hauteur issue de F du tétraèdre ACHF. Un vecteur normal à ce plan est donc $\vec{n}(1;-1;1)$.
- Par analogie avec le résultat précédent, préciser les hauteurs du tétraèdre ACHF issues respectivement des sommets A, C et H. Les quatre hauteurs du tétraèdre ACHF sont-elles concourantes ? La hauteur du tétraèdre $ACHF$ issue de $A$ est $[AG]$, celle issue de $C$ est $[CE]$ et celle issue de $H$ est $[BH]$.
$A(0;0;0)$ donc $0-0+0=0$ : les coordonnées du point $A$ sont solution de l’équation cartésienne fournie.
$C(1;1;0)$ donc $1-1+0=0$ : les coordonnées du point $C$ sont solution de l’équation cartésienne fournie.
$H(0;1;1)$ donc $0-1+1=0$ : les coordonnées du point $H$ sont solution de l’équation cartésienne fournie.
Une équation cartésienne su plan $(ACH)$ est donc $x-y+z=0$.
$\quad$
Or les coordonnées de $F$ sont $(1;0;1)$ et celles de $D$ sont $(0;1;0)$.
On a donc $\vec{FD}(-1;1;-1)$. Ainsi $\vec{FD}=-\vec{n}$.
Le vecteur $\vec{FD}$ est par conséquent normal au plan $(ACH)$ et la droite $(FD)$ est la hauteur issue de $F$ du tétraèdre $ACHF$.
$\quad$
Ces quatre hauteurs se coupent en $O$ le centre du carré. Elles sont donc concourantes.
$\quad$
Partie B Une propriété des tétraèdres orthocentriques
Dans cette partie, on considère un tétraèdre MNPQ dont les hauteurs issues des sommets M et N sont sécantes en un point K. Les droites (MK) et (NK) sont donc orthogonales aux plans (NPQ) et (MPQ) respectivement.
-
- Justifier que la droite (PQ) est orthogonale à la droite (MK) ; on admet de même que les droites (PQ) et (NK) sont orthogonales. La droite $(MK)$ est orthogonale au plan $(NPQ)$. Elle est donc orthogonale à toutes les droites de ce plan, en particulier $(PQ)$.
- Que peut-on déduire de la question précédente relativement à la droite (PQ) et au plan (MNK) ? Justifier la réponse. La droite $(PQ)$ est donc orthogonale à deux droites sécantes du plan $(MNK)$. Elle est donc orthogonale à ce plan.
$\quad$
$\quad$ - Montrer que les arêtes [MN] et [PQ] sont orthogonales. Ainsi, on obtient la propriété suivante : Si un tétraèdre est orthocentrique, alors ses arêtes opposées sont orthogonales deux à deux.
(On dit que deux arêtes d'un tétraèdre sont « opposées» lorsqu'elles n'ont pas de sommet commun.) La droite $(PQ)$ est orthogonale au plan $(MNK)$. Elle est donc orthogonale à toutes les droites de ce plan, en particulier à $(MN)$.
Ainsi les arêtes $[MN]$ et $[PQ]$ sont orthogonales.
$\quad$
Partie C Application
Dans un repère orthonormé, on considère les points : \[\text{R}(-3~;~5~;~2) ,\text{S}(1~;~4~;~-2) , \text{T}(4~;~-1~;~5)\quad \text{et U}(4~;~7~;~3).\] Le tétraèdre RSTU est-il orthocentrique ? Justifier.On a $\vec{RT}(7;-6;3)$ et $\vec{SU}(3;3;5)$.
Donc $\vec{RT}.\vec{SU}=3\times 7-6\times 3+3\times 5=18\neq 0$.D’après la contraposée de la propriété donnée à la fin de la partie B le tétraèdre $RSTU$ n’est pas orthocentrique.
$\quad$
Exercice 4 5 points
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On pose $z_0 = 8$ et, pour tout entier naturel $n$ : \[z_{n+1} = \dfrac{3 - \text{i}\sqrt{3}}{4}z_n.\] On note $A_n$ le point du plan d'affixe $z_n$.
-
- Vérifier que : \[\dfrac{3 - \text{i}\sqrt{3}}{4} = \dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}}.\]
- En déduire l'écriture de chacun des nombres complexes $z_1$, $z_2$ et $z_3$ sous forme exponentielle et vérifier que $z_3$ est un imaginaire pur dont on précisera la partie imaginaire.
- Représenter graphiquement les points $A_0$ , $A_1$ , $A_2$ et $A_3$ ; on prendra pour unité le centimètre.
-
- Démontrer par récurrence que, pour tout entier naturel $n$, \[z_n = 8 \times \left(\dfrac{\sqrt{3}}{2}\right)^n \text{e}^{- \text{i}\frac{n\pi}{6}}.\]
- Pour tout entier naturel $n$, on pose $u_n = \left|z_n\right|$. Déterminer la nature et la limite de la suite $\left(u_n\right)$.
-
- Démontrer que, pour tout entier naturel $k$, \[\dfrac{z_{k+1} - z_{k}}{z_{k+1}} = - \dfrac{1}{\sqrt{3}}\text{i}.\] En déduire que, pour tout entier naturel $k$, on a l'égalité : $A_kA_{k+1} = \dfrac{1}{\sqrt{3}} \text{O}A_{k+1}$.
- Pour tout entier naturel $n$, on appelle $\ell_n$ la longueur de la ligne brisée reliant dans cet ordre les points $A_0$,$\:$ $A_1$,$\:$ $A_2$, $\ldots$ , $A_n$.
On a ainsi : $\ell_n = A_0A_1 + A_1A_2 + \ldots + A_{n-1}A_n$.
Démontrer que la suite $\left(\ell_n\right)$ est convergente et calculer sa limite.
Correction de l'exercice 4 5 points
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On pose $z_0 = 8$ et, pour tout entier naturel $n$ : \[z_{n+1} = \dfrac{3 - \text{i}\sqrt{3}}{4}z_n.\] On note $A_n$ le point du plan d'affixe $z_n$.
-
- Vérifier que : \[\dfrac{3 - \text{i}\sqrt{3}}{4} = \dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}}.\] $\begin{align*} \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6}&=\dfrac{\sqrt{3}}{2}\left(\cos\left(-\dfrac{\pi}{6}\right)+\text{i} \sin \left(-\dfrac{\pi}{6}\right)\right) \\
- En déduire l'écriture de chacun des nombres complexes $z_1$, $z_2$ et $z_3$ sous forme exponentielle et vérifier que $z_3$ est un imaginaire pur dont on précisera la partie imaginaire. On a donc :
- Représenter graphiquement les points $A_0$ , $A_1$ , $A_2$ et $A_3$ ; on prendra pour unité le centimètre.
&=\dfrac{\sqrt{3}}{2}\left(\dfrac{\sqrt{3}}{2}-\dfrac{\text{i}}{2}\right) \\
&=\dfrac{3}{4}-\dfrac{\text{i}\sqrt{3}}{4} \\
&=\dfrac{3-\text{i}\sqrt{3}}{4}
\end{align*}$
$\quad$
$z_1=\dfrac{3-\text{i}\sqrt{3}}{4} \times 8 =8 \times \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} = 4\sqrt{3}\text{e}^{-\text{i}\pi/6}$
$z_2=\dfrac{3-\text{i}\sqrt{3}}{4} \times 4\sqrt{3}\text{e}^{-\text{i}\pi/6} = 4\sqrt{3}\text{e}^{-\text{i}\pi/6} \times \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} = 6\text{e}^{-\text{i} \pi/3}$
$z_3=\dfrac{3-\text{i}\sqrt{3}}{4} \times 6\text{e}^{-\text{i} \pi/3} = \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} \times 6\text{e}^{-\text{i} \pi/3}=3\sqrt{3}\text{e}^{-\text{i}\pi/2}$
On a donc $z_3=-3\text{i}\sqrt{3}$ est un nombre imaginaire pur dont la partie imaginaire est $-3\sqrt{3}$.
$\quad$
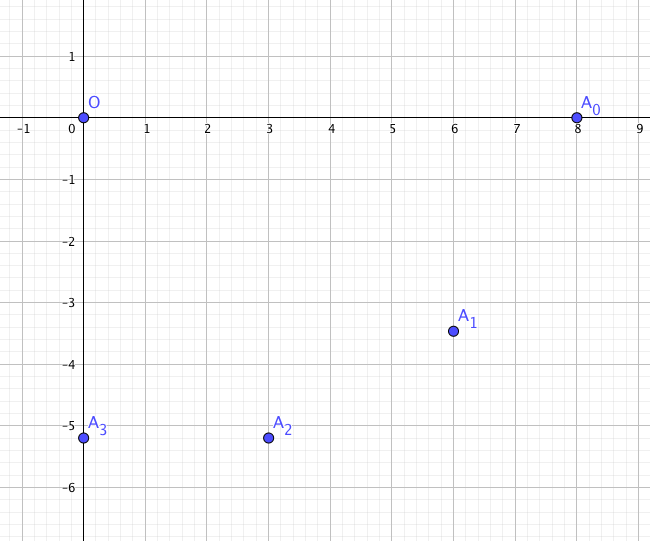
-
- Démontrer par récurrence que, pour tout entier naturel $n$, \[z_n = 8 \times \left(\dfrac{\sqrt{3}}{2}\right)^n \text{e}^{- \text{i}\frac{n\pi}{6}}.\] Initialisation : Si $n=0$ alors $8\times \left(\dfrac{\sqrt{3}}{2}\right)^0\text{e}{0}=8=z_0$.
- Pour tout entier naturel $n$, on pose $u_n = \left|z_n\right|$. Déterminer la nature et la limite de la suite $\left(u_n\right)$. Pour tout entier naturel $n$ on a :
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons vraie la propriété au rang $n$ : $z_n=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}$.
Montrons qu’elle est vraie au rang suivant : $z_{n+1}=8\times \left(\dfrac{\sqrt{3}}{2}\right)^{n+1}\times \text{e}^{-\text{i} (n+1) \pi/6}$
$\begin{align*} z_{n+1}&= \dfrac{3-\text{i}\sqrt{3}}{4}z_n \\
&=\dfrac{\sqrt{3}}{2}\text{e}^{-\text{i} \pi/6} \times 8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}\\
&=8\times \left(\dfrac{\sqrt{3}}{2}\right)^{n+1}\times \text{e}^{-\text{i} (n+1) \pi/6}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $z_n=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}$.
$\quad$
$u_n=\left|z_n\right|=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n$.
La suite $\left(u_n\right)$ est donc géométrique de raison $\dfrac{\sqrt{3}}{2}$ et de premier terme $u_0=8$
Or $-1< \dfrac{\sqrt{3}}{2} <1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{\sqrt{3}}{2}\right)^n=0$
et $\lim\limits_{n \to +\infty} u_n=0$.
$\quad$ -
- Démontrer que, pour tout entier naturel $k$, \[\dfrac{z_{k+1} - z_{k}}{z_{k+1}} = - \dfrac{1}{\sqrt{3}}\text{i}.\] En déduire que, pour tout entier naturel $k$, on a l'égalité : $A_kA_{k+1} = \dfrac{1}{\sqrt{3}} \text{O}A_{k+1}$. Pour tout entier naturel $k$ on a :
- Pour tout entier naturel $n$, on appelle $\ell_n$ la longueur de la ligne brisée reliant dans cet ordre les points $A_0$,$\:$ $A_1$,$\:$ $A_2$, $\ldots$ , $A_n$.
On a ainsi : $\ell_n = A_0A_1 + A_1A_2 + \ldots + A_{n-1}A_n$.
Démontrer que la suite $\left(\ell_n\right)$ est convergente et calculer sa limite. Pour tout entier naturel $n$ on a :
$\begin{align*} \dfrac{z_{k+1}-z_k}{z_{k+1}} &=1-\dfrac{z_k}{z_{k+1}} \\
&=1-\dfrac{ 8\times \left(\dfrac{\sqrt{3}}{2}\right)^k\times \text{e}^{-\text{i} k \pi/6}}{8\times \left(\dfrac{\sqrt{3}}{2}\right)^{k+1}\times \text{e}^{-\text{i} (k+1) \pi/6}} \\
&=1-\dfrac{1}{\dfrac{\sqrt{3}}{2}\text{e}^{\text{i}\pi/6}} \\
&=1-\dfrac{2\text{e}^{\text{i} \pi/6}}{\sqrt{3}} \\
&=1-\dfrac{2}{\sqrt{3}}\left(\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right) \\
&=1-1-\dfrac{1}{\sqrt{3}}\text{i} \\
&=-\dfrac{1}{\sqrt{3}}\text{i}
\end{align*}$
$\quad$
Cela signifie donc que $\left|\dfrac{z_{k+1}-z_k}{z_{k+1}}\right|=\dfrac{1}{\sqrt{3}} \iff \dfrac{A_kA_{k+1}}{OA_{k+1}}=\dfrac{1}{\sqrt{3}}$
Soit $A_kA_{k+1}=\dfrac{1}{\sqrt{3}}OA_{k+1}$.
$\quad$
$\begin{align*} \ell_n=\dfrac{1}{\sqrt{3}}OA_1+\dfrac{1}{\sqrt{3}}OA_2+\ldots +\dfrac{1}{\sqrt{3}}OA_n \\
&=\dfrac{1}{\sqrt{3}}\left(u_1+u_2+\ldots+u_n\right) \\
&=\dfrac{1}{\sqrt{3}}\times u_1\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}} \\
&=\dfrac{4\sqrt{3}}{\sqrt{3}}\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}} \\
&=4\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}}
\end{align*}$
Or $\lim\limits_{n \to +\infty} \left(\dfrac{\sqrt{3}}{2}\right)^n=0$
Donc $\lim\limits_{n \to \infty} \ell_n= \dfrac{4}{1-\dfrac{\sqrt{3}}{2}}= \dfrac{8}{2-\sqrt{3}} \approx 29,86 $
La suite $\left(\ell_n\right)$ est bien convergente.
$\quad$
Spécialité 5 points
Partie A
On considère l'équation suivante dont les inconnues $x$ et $y$ sont des entiers naturels : \[x^2 - 8y^2 = 1 . \quad(E)\]
- Déterminer un couple solution $(x~;~y)$ où $x$ et $y$ sont deux entiers naturels.
- On considère la matrice $A = \begin{pmatrix}3&8\\1&3\end{pmatrix}$. On définit les suites d'entiers naturels $\left(x_n\right)$ et $\left(y_n\right)$ par : \[x_0 = 1,\: y_0 = 0,\: \text{et pour tout entier naturel }\:n,\: \begin{pmatrix}x_{n+1}\\y_{n+1}\end{pmatrix} = A\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix}.\]
- Démontrer par récurrence que pour tout entier naturel $n$, le couple $\left(x_n~;~y_n\right)$ est solution de l'équation $(E)$.
- En admettant que la suite $\left(x_n\right)$ est à valeurs strictement positives, démontrer que pour tout entier naturel $n$, on a : $x_{n+1} > x_n$.
- En déduire que l'équation $(E)$ admet une infinité de couples solutions.
Partie B
Un entier naturel $n$ est appelé un nombre puissant lorsque, pour tout diviseur premier $p$ de $n$,$\:$ $p^2$ divise $n$.
- Vérifier qu'il existe deux nombres entiers consécutifs inférieurs à $10$ qui sont puissants.
L'objectif de cette partie est de démontrer, à l'aide des résultats de la partie A, qu'il existe une infinité de couples de nombres entiers naturels consécutifs puissants et d'en trouver quelques exemples. - Soient $a$ et $b$ deux entiers naturels. Montrer que l'entier naturel $n = a^2 b^3$ est un nombre puissant.
- Montrer que si $(x~;~y)$ est un couple solution de l'équation $(E)$ définie dans la partie A, alors $x^2 - 1$ et $x^2$ sont des entiers consécutifs puissants.
- Conclure quant à l'objectif fixé pour cette partie, en démontrant qu'il existe une infinité de couples de nombres entiers consécutifs puissants.
Déterminer deux nombres entiers consécutifs puissants supérieurs à $2018$.
Correction de l'exercice de Spécialité 5 points
Partie A
On considère l'équation suivante dont les inconnues $x$ et $y$ sont des entiers naturels : \[x^2 - 8y^2 = 1 . \quad(E)\]
- Déterminer un couple solution $(x~;~y)$ où $x$ et $y$ sont deux entiers naturels. $3^2-8\times 1^2=9-8=1$.
- On considère la matrice $A = \begin{pmatrix}3&8\\1&3\end{pmatrix}$. On définit les suites d'entiers naturels $\left(x_n\right)$ et $\left(y_n\right)$ par : \[x_0 = 1,\: y_0 = 0,\: \text{et pour tout entier naturel }\:n,\: \begin{pmatrix}x_{n+1}\\y_{n+1}\end{pmatrix} = A\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix}.\]
- Démontrer par récurrence que pour tout entier naturel $n$, le couple $\left(x_n~;~y_n\right)$ est solution de l'équation $(E)$. Initialisation : Si $n=0$ alors $1^2-8\times 0^2=1$. Le couple $\left(x_0;y_0\right)$ est donc solution de l’équation $(E)$.
- En admettant que la suite $\left(x_n\right)$ est à valeurs strictement positives, démontrer que pour tout entier naturel $n$, on a : $x_{n+1} > x_n$. Pour tout entier naturel $n$ on a :
$\quad$
Hérédité : Supposons la propriété vraie au rang $p$ : $\left(x_p;y_p\right)$ est solution de l’équation $(E)$.
Ainsi $x_p^2-8y_p^2=1$
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $\left(x_{p+1};y_{p+1}\right)$ est solution de l’équation $(E)$.
On a $\begin{pmatrix} x_{p+1}\\y_{p+1}\end{pmatrix}=\begin{pmatrix}3x_p+8y_p\\x_p+3y_p\end{pmatrix}$.
Ainsi :
$\begin{align*} \left(x_{p+1}\right)^2-8\left(y_{p+1}\right)^2 &= \left(3x_p+8y_p\right)^2-8\left(x_p+3y_p\right)^2 \\
&=9{x_p}^2+64{y_p}^2+48x_py_p-8\left({x_p}^2+9{y_p}^2+6x_py_p\right) \\
&=9{x_p}^2+64{y_p}^2+48x_py_p-8{x_p}^2-72{y_p}^2-48x_py_p \\
&={x_p}^2-8{y_p}^2 \\
&=1 \text{ d'après l'hypothèse de récurrence}
\end{align*}$
La propriété est vraie au rang $p+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ le couple $\left(x_n;y_n\right)$ est solution de l’équation $(E)$.
$\quad$
$x_{n+1}-x_n=3x_n+8y_n-x_n=2x_n+8y_n>0$ puisque $x_n$ et $y_n$ sont des entiers naturels et $x_n>0$.
$\quad$ - En déduire que l'équation $(E)$ admet une infinité de couples solutions. La suite $\left(x_n\right)$ est donc une suite strictement croissante d’entiers naturels.
Le couple $(3;1)$ est donc solution de l’équation $(E)$.
$\quad$
L’équation $(E)$ admet donc une infinité de couples solutions.
$\quad$
Partie B
Un entier naturel $n$ est appelé un nombre puissant lorsque, pour tout diviseur premier $p$ de $n$,$\:$ $p^2$ divise $n$.
- Vérifier qu'il existe deux nombres entiers consécutifs inférieurs à $10$ qui sont puissants.
L'objectif de cette partie est de démontrer, à l'aide des résultats de la partie A, qu'il existe une infinité de couples de nombres entiers naturels consécutifs puissants et d'en trouver quelques exemples. Le seul nombre premier qui divise $8$ est $2$ et $8$ est divisible par $2^2=4$. - Soient $a$ et $b$ deux entiers naturels. Montrer que l'entier naturel $n = a^2 b^3$ est un nombre puissant. Les diviseurs premiers de $n$ sont les diviseurs premiers de $a$ ou de $b$.
- Montrer que si $(x~;~y)$ est un couple solution de l'équation $(E)$ définie dans la partie A, alors $x^2 - 1$ et $x^2$ sont des entiers consécutifs puissants. Soit $(x;y)$ un couple solution de l’équation $(E)$.
- Conclure quant à l'objectif fixé pour cette partie, en démontrant qu'il existe une infinité de couples de nombres entiers consécutifs puissants.
Déterminer deux nombres entiers consécutifs puissants supérieurs à $2018$. D’après la question A.3. il existe une infinité de couples solutions à l’équation $(E)$.
Le seul nombre premier qui divise $9$ est $3$ et $9$ est divisible par $3^2=9$.
Ces deux entiers consécutifs sont donc puissants.
Soit $p$ un diviseur premier de $a$. Il existe alors un entier naturel $q$ tel que $a=pq$.
Donc $n=p^2q^2b^3$ et $p^2$ divise $n$.
Soit $r$ un diviseur premier de $b$. Il existe alors un entier naturel $s$ tel que $b=rs$.
Donc $n=a^2r^3s^3=a^2r^2rs^3$ et $r^2$ divise $n$.
$n$ est donc un nombre puissant.
Ainsi $x^2-8y^2=1$ soit $x^2-1=8y^2=2^3y^2$.
D’après la question précédente, le nombre $x^2-1$ est puissant.
Les seuls diviseurs premiers de $x^2$ sont les diviseurs premiers de $x$.
Si $p$ est diviseur premier de $x$, il existe alors un entier naturel $q$ tel que $x=pq$.
Donc $x^2=p^2q^2$ et $p^2$ divise $x^2$.
$x^2$ est donc un nombre puissant.
Remarque : On pouvait également dire que $x^2=1^3\times x^2$ et appliquer la propriété précédente.
$\quad$
Ainsi, $x^2-1$ et $x^2$ sont deux entiers naturels consécutifs puissants.
$\quad$
La question précédente nous indique que pour chaque couple solution on peut déterminer deux entiers consécutifs puissants.
Il existe donc une infinité de couples de nombres entiers consécutifs puissants.
$\quad$
On a, à l’aide de la calculatrice $\begin{pmatrix} x_3\\y_3\end{pmatrix}=\begin{pmatrix} 99\\35\end{pmatrix}$
Donc $99^2=9~801$ et $99^2-1=9~800$ sont puissants.
$\quad$ -
-
- Vues: 33358
