Baccalauréat S Asie 21 juin 2018
Exercice 1 6 points
Une ferme aquatique exploite une population de crevettes qui évolue en fonction de la reproduction naturelle et des prélèvements effectués. La masse initiale de celte population de crevettes est estimée à $100$ tonnes. Compte tenu des conditions de reproduction et de prélèvement, on modélise la masse de la population de crevettes, exprimée en tonne, en fonction du temps, exprimé en semaine, par la fonction $f_P$, définie sur l'intervalle $[0~;~ +\infty[$ par : \[f_P(t) = \dfrac{100p}{1 - (1 - p)\text{e}^{- pt}}\] où $p$ est un paramètre strictement compris entre $0$ et $1$ et qui dépend des différentes conditions de vie et d'exploitation des crevettes.
- Cohérence du modèle
- Calculer $f_p(0)$.
- On rappelle que $0 < p < 1$. Démontrer que pour tout nombre réel $t \geqslant 0$, $1 - (1 - p)\text{e}^{- pt} \geqslant p$.
- En déduire que pour tout nombre réel $t \geqslant 0$, $0 < f_P(t) \leqslant 100$.
- Étude de l'évolution lorsque $p = 0,9$ Dans cette question, on prend $p = 0,9$ et on étudie la fonction $f_{0.9}$ définie sur $[0~;~ +\infty[$ par : \[f_{0,9}(t) = \dfrac{90}{1 - 0,1 \text{e}^{- 0,9t}}.\]
- Déterminer les variations de la fonction $f_{0.9}$.
- Démontrer pour tout nombre réel $t \geqslant 0$, $f_{0,9}(t) \geqslant 90$.
- Interpréter les résultats des questions 2. a. et 2. b. dans le contexte.
- Retour au cas général On rappelle que $0 < p < 1$. Exprimer en fonction de $p$ la limite de $f_P$ lorsque $t$ tend vers $+ \infty$.
- Dans cette question, on prend $p = \dfrac{1}{2}$.
- Montrer que la fonction $H$ définie sur l'intervalle $[0~;~ +\infty[$ par: \[H(t) = 100\ln \left(2 - \text{e}^{- \frac{t}{2}}\right) + 50t\] est une primitive de la fonction $f_{1/2}$ sur cet intervalle.
- En déduire la masse moyenne de crevettes lors des 5 premières semaines d'exploitation, c'est-à-dire la valeur moyenne de la fonction $f_{1/2}$ sur l'intervalle $[0~;~5]$. En donner une valeur approchée arrondie à la tonne.
Correction de l'exercice 1 (5 points)
Une ferme aquatique exploite une population de crevettes qui évolue en fonction de la reproduction naturelle et des prélèvements effectués. La masse initiale de celte population de crevettes est estimée à $100$ tonnes. Compte tenu des conditions de reproduction et de prélèvement, on modélise la masse de la population de crevettes, exprimée en tonne, en fonction du temps, exprimé en semaine, par la fonction $f_P$, définie sur l'intervalle $[0~;~ +\infty[$ par : \[f_P(t) = \dfrac{100p}{1 - (1 - p)\text{e}^{- pt}}\] où $p$ est un paramètre strictement compris entre $0$ et $1$ et qui dépend des différentes conditions de vie et d'exploitation des crevettes.
- Cohérence du modèle
- Calculer $f_p(0)$. $f_p(0)=\dfrac{100p}{1-(1-p)}=\dfrac{100p}{p}=100$.
- On rappelle que $0 < p < 1$. Démontrer que pour tout nombre réel $t \geqslant 0$, $1 - (1 - p)\text{e}^{- pt} \geqslant p$. Pour tout nombre réel $t \geq 0$ on a $-pt\leq 0$ donc $0 < \text{e}^{-pt} \leq 1$.
- En déduire que pour tout nombre réel $t \geqslant 0$, $0 < f_P(t) \leqslant 100$. Pour tout nombre réel $t \geq 0$ on a :
$\quad$
Par conséquent $ 0 < (1-p)\text{e}^{-pt} \leq 1-p$
Ainsi $-(1-p)\text{e}^{-pt} \geq p-1$
On obtient alors $1-(1-p)\text{e}^{-pt} \geq p$.
$\quad$
$\begin{align*} 1-(1-p)\text{e}^{-pt} \geq p &\iff 0< \dfrac{1}{1-(1-p)\text{e}^{-pt}} \leq \dfrac{1}{p} \\
&=0 < f_p(t) \leq 100 \end{align*}$
$\quad$ - Étude de l'évolution lorsque $p = 0,9$ Dans cette question, on prend $p = 0,9$ et on étudie la fonction $f_{0.9}$ définie sur $[0~;~ +\infty[$ par : \[f_{0,9}(t) = \dfrac{90}{1 - 0,1 \text{e}^{- 0,9t}}.\]
- Déterminer les variations de la fonction $f_{0.9}$. La fonction $t \mapsto -0,9t$ est strictement décroissante sur $[0;+\infty[$.
- Démontrer pour tout nombre réel $t \geqslant 0$, $f_{0,9}(t) \geqslant 90$. $\lim\limits_{t \to +\infty} -0,9t=-\infty$ et $\lim\limits_{T \to -\infty} \text{e}^{-0,9t}=0$ donc $\lim\limits_{t \to +\infty} \text{e}^{-0,9t}=0$.
- Interpréter les résultats des questions 2. a. et 2. b. dans le contexte. La masse de cette population de crevettes va continuelle décroître mais sera toujours supérieure à $90$ tonnes.
La fonction exponentielle est strictement croissante sur $\mathbb R$. Donc la fonction $t \mapsto \text{e}^{-0,9t}$ est strictement décroissante sur $[0;+\infty[$.
Par conséquent la fonction $t\mapsto 1-0,1\text{e}^{-0,9t}$ est strictement croissante sur $[0;+\infty[$.
Finalement la fonction $f_{0,9}$ est décroissante sur l’intervalle $[0;+\infty[$.
Remarque : On peut évidemment dériver cette fonction pour étudier ses variations.
$\quad$
Par conséquent $\lim\limits_{t\to +\infty} f_{0,9}(t)=90$.
D’après la question précédente, la fonction $f_{0,9}$ est strictement décroissante sur $[0;+\infty[$.
Cela signifie donc que, pour tout nombre $t\geq 0$ on a $f_{0,9}(t) \geq 90$.
$\quad$
$\quad$ - Retour au cas général On rappelle que $0 < p < 1$. Exprimer en fonction de $p$ la limite de $f_P$ lorsque $t$ tend vers $+ \infty$. Pour tout réel $p$ vérifiant $0<p<1$ on a
- Dans cette question, on prend $p = \dfrac{1}{2}$.
- Montrer que la fonction $H$ définie sur l'intervalle $[0~;~ +\infty[$ par: \[H(t) = 100\ln \left(2 - \text{e}^{- \frac{t}{2}}\right) + 50t\] est une primitive de la fonction $f_{1/2}$ sur cet intervalle. La fonction $H$ est dérivable sur $[0;+\infty[$ en tant que composée de fonctions dérivables.
- En déduire la masse moyenne de crevettes lors des 5 premières semaines d'exploitation, c'est-à-dire la valeur moyenne de la fonction $f_{1/2}$ sur l'intervalle $[0~;~5]$. En donner une valeur approchée arrondie à la tonne. La masse moyenne cherchée est :
$$\begin{array} {ll} H'(t)&=100\times \dfrac{-\left(-\dfrac{1}{2}\text{e}^{-t/2}\right)}{2-\text{e}^{-t/2}}+50 \\ &=\dfrac{50\text{e}^{-t/2}+50\left(2-\text{e}^{-t/2}\right)}{2-\text{e}^{-t/2} }\\ &=\dfrac{100}{2-\text{e}^{-t/2}} \\ &=\dfrac{50}{1-0,5\text{e}^{-t/2}}\\ & =f_{1/2}(t) \end{array}$$
Pour tout nombre réel $t \geq 0$ on a $\text{e}^{0,5t}-0,5 > 0$
Ainsi une primitive de la fonction $f_{1/2}$ est la fonction $F$ définie sur l’intervalle $[0;+\infty[$ par :
$\begin{align*} F(t)&=100\ln\left(\text{e}^{0,5t}-0,5\right) \\
&=100\ln\left(\text{e}^{0,5t}\left(1-0,5\text{e}^{-0,5t}\right)\right)\\
&=100\ln\left(\text{e}^{0,5t}\right)+100\ln\left(1-0,5\text{e}^{-0,5t}\right)\\
&=50t+100\ln\left(\dfrac{2-\text{e}^{-0,5t}}{2}\right) \\
&=50t+100\ln\left(2-\text{e}^{-0,5t}\right)-100\ln(2) \\
&=H(t)-100\ln(2)
\end{align*}$
La fonction $H$ est donc une primitive de la fonction $f_{1/2}$ sur l’intervalle $[0;+\infty[$.
$\quad$
$\begin{align*} \displaystyle m&=\dfrac{1}{5-0}\int_0^5 f_{1/2}(t)\text{d}t \\
&=\dfrac{1}{5}\left(H(5)-H(0)\right) \\
&=\dfrac{1}{5}\left(100\ln\left(2-\text{e}^{-2,5}\right)+250\right) \\
&=20\ln\left(2-\text{e}^{-2,5}\right)+50\\
&\approx 63
\end{align*}$
$\quad$
$\lim\limits_{t \to +\infty} -pt=-\infty$ et $\lim\limits_{T \to -\infty} \text{e}^{-pt}=0$ donc $\lim\limits_{t \to +\infty} \text{e}^{-pt}=0$.
Par conséquent $\lim\limits_{t \to +\infty} 1-(1-p)\text{e}^{-pt}=1$
Et $\lim\limits_{t \to +\infty} f_p(t)=100p$.
$\quad$
Exercice 2 5 points
Dans les parties A et B de cet exercice, on considère une maladie ; tout individu a une probabilité égale à $0,15$ d'être touché par cette maladie.
Partie A
Cette partie est un questionnaire à choix multiples (Q. C. M.). Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n'est demandée. Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte ni n'enlève aucun point.
Un test de dépistage de cette maladie a été mis au point. Si l'individu est malade, dans 94 % des cas le test est positif. Pour un individu choisi au hasard dans cette population, la probabilité que le test soit positif vaut $0,158$.
- On teste un individu choisi au hasard dans la population : le test est positif. Une valeur arrondie au centième de la probabilité que la personne soit malade est égale à :
$$\begin{array}{cccc} \textbf{A :} 0,94 &\textbf{B :} 1 &\textbf{C :} 0,89 &\textbf{D :} \text{on ne peut pas savoir} \end{array}$$ - On prélève un échantillon aléatoire dans la population, et on fait passer le test aux individus de cet échantillon. On souhaite que la probabilité qu'au moins un individu soit testé positivement soit supérieure ou égale à $0,99$. La taille minimum de l'échantillon doit être égale à :
$$\begin{array}{cccc} \textbf{A :}\text{ 26 personnes } &\textbf{B :} \text{27 personnes }&\textbf{C :} \text{3 personnes } &\textbf{D :} \text{7 personnes} \end{array}$$ - Un vaccin pour lutter contre cette maladie a été mis au point. II est fabriqué par une entreprise sous forme de dose injectable par seringue. Le volume $V$ (exprimé en millilitre) d'une dose suit une loi normale d'espérance $\mu = 2$ et d'écart-type $\sigma$. La probabilité que le volume d'une dose, exprimé en millilitre, soit compris entre $1,99$ et $2,01$ millilitres est égale à $0,997$. La valeur de $\sigma$ doit vérifier:
$$\begin{array}{cccc} \textbf{A :} \sigma = 0,02 &\textbf{B :} \sigma < 0,003 &\textbf{C :} \sigma > 0,003 &\textbf{D :} \sigma = 0,003 \end{array}$$
Partie B
- Une boîte d'un certain médicament permet de soigner un malade. La durée d'efficacité (exprimée en mois) de ce médicament est modélisée de la manière suivante :
- durant les $12$ premiers mois après fabrication, on est certain qu'il demeure efficace ;
- au-delà, sa durée d'efficacité restante suit une loi exponentielle de paramètre $\lambda$.
- Une ville de $100\;000$ habitants veut constituer un stock de ces boîtes afin de soigner les personnes malades. Quelle doit être la taille minimale de ce stock pour que la probabilité qu'il suffise à soigner tous les malades de cette ville soit supérieure à $95$ % ?
Correction de l'exercice 2 (5 points)
Dans les parties A et B de cet exercice, on considère une maladie ; tout individu a une probabilité égale à $0,15$ d'être touché par cette maladie.
Partie A
Cette partie est un questionnaire à choix multiples (Q. C. M.). Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n'est demandée. Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte ni n'enlève aucun point.
Un test de dépistage de cette maladie a été mis au point. Si l'individu est malade, dans 94 % des cas le test est positif. Pour un individu choisi au hasard dans cette population, la probabilité que le test soit positif vaut $0,158$.
- On teste un individu choisi au hasard dans la population : le test est positif. Une valeur arrondie au centième de la probabilité que la personne soit malade est égale à :
$$\begin{array}{cccc} \textbf{A :} 0,94 &\textbf{B :} 1 &\textbf{C :} 0,89 &\textbf{D :} \text{on ne peut pas savoir} \end{array}$$ On appelle $M$ l’événement “l’individu est touché par la maladie” et $T$ l’événement “le test est positif”. - On prélève un échantillon aléatoire dans la population, et on fait passer le test aux individus de cet échantillon. On souhaite que la probabilité qu'au moins un individu soit testé positivement soit supérieure ou égale à $0,99$. La taille minimum de l'échantillon doit être égale à :
$$\begin{array}{cccc} \textbf{A :}\text{ 26 personnes } &\textbf{B :} \text{27 personnes }&\textbf{C :} \text{3 personnes } &\textbf{D :} \text{7 personnes} \end{array}$$ On effectue $n$ tirages indépendants, aléatoires et identiques. - Un vaccin pour lutter contre cette maladie a été mis au point. II est fabriqué par une entreprise sous forme de dose injectable par seringue. Le volume $V$ (exprimé en millilitre) d'une dose suit une loi normale d'espérance $\mu = 2$ et d'écart-type $\sigma$. La probabilité que le volume d'une dose, exprimé en millilitre, soit compris entre $1,99$ et $2,01$ millilitres est égale à $0,997$. La valeur de $\sigma$ doit vérifier:
$$\begin{array}{cccc} \textbf{A :} \sigma = 0,02 &\textbf{B :} \sigma < 0,003 &\textbf{C :} \sigma > 0,003 &\textbf{D :} \sigma = 0,003 \end{array}$$ La variable aléatoire $Z=\dfrac{V-2}{\sigma}$ suit la loi normale centrée réduite.
On a ainsi $p(M)=0,15$, $p(T)=0,158$ et $p_M(T)=0,94$.
Par conséquent :
$\begin{align*} p_T(M)&=\dfrac{p(T\cap M)}{p(T)} \\
&=\dfrac{0,15\times 0,94}{0,158} \\
&\approx 0,89
\end{align*}$
Réponse C
$\quad$
À chaque tirage il y a deux issues : $T$ et $\overline{T}$.
De plus $p(T)=0,158$.
La variable aléatoire $X$ comptant le nombre d’individu testé positivement suit donc la loi binomiale de paramètres $n$ et $p=0,158$.
$\begin{align*} p(X \geq 1) \geq 0,99&\iff 1-p(X=0) \geq 0,99 \\
&\iff 1-(1-0,158)^n \geq 0,99 \\
&\iff -0,842^n \geq -0,01 \\
&\iff 0,842^n \leq 0,01 \\
&\iff n\ln(0,842) \leq \ln (0,01) \\
&\iff n \geq \dfrac{\ln (0,01)}{\ln(0,842)}
\end{align*}$
Or $\dfrac{\ln (0,01)}{\ln(0,842)}\approx 26,8$
Donc $n \geq 27$.
Réponse B
$\quad$
$\begin{align*} p(1,99 \leq V \leq 2,01)=0,997 &\iff p(-0,01 \leq V-2 \leq 0,1)=0,997 \\
&\iff p\left(-\dfrac{0,01}{\sigma} \leq \dfrac{V-2}{\sigma} \leq \dfrac{0,1}{\sigma}\right)=0,997 \\
&\iff p\left(-\dfrac{0,01}{\sigma} \leq Z \leq \dfrac{0,1}{\sigma}\right)=0,997 \\
&\iff 2p\left(Z\leq \dfrac{0,01}{\sigma}\right)-1=0,997 \\
&\iff 2p\left(Z\leq \dfrac{0,01}{\sigma}\right)=1,997 \\
&\iff p\left(Z\leq \dfrac{0,01}{\sigma}\right)=0,998~5
\end{align*}$
À l’aide de la touche inverse loi normale de la calculatrice on trouve $\dfrac{0,01}{\sigma}\approx 2,967~73$ donc $\sigma \approx 0,00337>0,003$
Réponse C
$\quad$
Partie B
- Une boîte d'un certain médicament permet de soigner un malade. La durée d'efficacité (exprimée en mois) de ce médicament est modélisée de la manière suivante :
- durant les $12$ premiers mois après fabrication, on est certain qu'il demeure efficace ;
- au-delà, sa durée d'efficacité restante suit une loi exponentielle de paramètre $\lambda$.
On appelle $B$ la variable aléatoire correspondant à la durée d’efficacité restante au delà des $12$ premiers mois. - Une ville de $100\;000$ habitants veut constituer un stock de ces boîtes afin de soigner les personnes malades. Quelle doit être la taille minimale de ce stock pour que la probabilité qu'il suffise à soigner tous les malades de cette ville soit supérieure à $95$ % ? La probabilité d’être touché par la maladie est $p=0,15$.
On sait donc que
$\begin{align*} p(M>18-12)=0,887 &\iff p(M>6)=0,887 \\
&\iff \text{e}^{-6\lambda}=0,887 \\
&\iff -6\lambda =\ln(0,887) \\
&\iff \lambda=-\dfrac{\ln(0,887)}{6}
\end{align*}$
$\quad$
On a $n=100~000$.
Donc $n\geq 30$, $np=15~000 \geq 5$ et $n(1-p)=85~000\geq 5$.
La borne supérieure, arrondie par excès, d’un intervalle de fluctuation asymptotique de la proportion d’individus touchés par cette maladie est donc :
$$0,15+1,96\sqrt{\dfrac{0,15\times 0,85}{100~000}} \approx 0,15~222$$
Il faut donc que la ville ait un stock d’au moins $15~222$ boîtes de médicament pour soigner tous les malades de cette ville avec une probabilité supérieure à $95\%$.
$\quad$
Exercice 3 5 points
On se place dans un repère orthonormé d'origine O et d'axes (O$x$), (O$y$) et (O$z$). Dans ce repère, on donne les points A$(- 3~;~0~;~0)$, B$(3~;~0~;~0)$ , C$\left(0~;~3\sqrt{3}~;~0\right)$ et D$\left(0~;~\sqrt{3}~;~2\sqrt{6}\right)$. On note H le milieu du segment [CD] et I le milieu du segment [BC]. 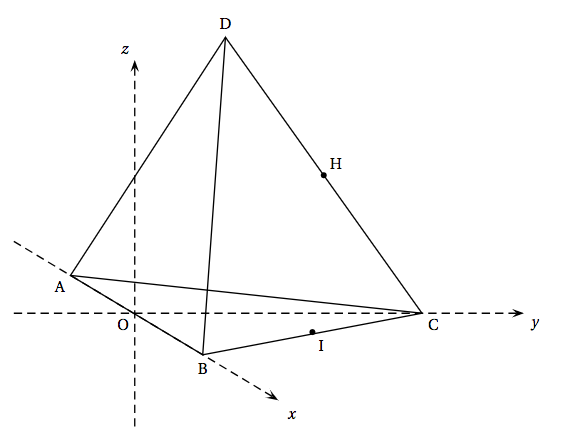
On admet pour la suite que toutes les arêtes du solide ABCD ont la même longueur, c'est-à-dire que le tétraèdre ABCD est un tétraèdre régulier. On appelle $\mathcal{P}$ le plan de vecteur normal $\vec{\text{OH}}$ et passant par le point I.
- Étude de la section du tétraèdre ABCD par le plan $\mathcal{P}$
- Montrer qu'une équation cartésienne du plan $\mathcal{P}$ est: $2y\sqrt{3} + z\sqrt{6} - 9 = 0$.
- Démontrer que le milieu J de [BD] est le point d'intersection de la droite (BD) et du plan $\mathcal{P}$.
- Donner une représentation paramétrique de la droite (AD), puis démontrer que le plans $\mathcal{P}$ et la droite (AD) sont sécants en un point K dont on déterminera les coordonnées.
- Démontrer que les droites (IJ) et (JK) sont perpendiculaires.
- Déterminer précisément la nature de la section du tétraèdre ABCD par le plan $\mathcal{P}$.
- Peut-on placer un point M sur l'arête [BD] tel que le triangle OIM soit rectangle en M ?
Correction de l'exercice 3 (5 points)
On se place dans un repère orthonormé d'origine O et d'axes (O$x$), (O$y$) et (O$z$). Dans ce repère, on donne les points A$(- 3~;~0~;~0)$, B$(3~;~0~;~0)$ , C$\left(0~;~3\sqrt{3}~;~0\right)$ et D$\left(0~;~\sqrt{3}~;~2\sqrt{6}\right)$. On note H le milieu du segment [CD] et I le milieu du segment [BC]. 
- Calculer les longueurs AB et AD. $AB=\sqrt{\left(3-(-3)\right)^2+0^2+0^2}=\sqrt{36}=6$
- Étude de la section du tétraèdre ABCD par le plan $\mathcal{P}$
- Montrer qu'une équation cartésienne du plan $\mathcal{P}$ est: $2y\sqrt{3} + z\sqrt{6} - 9 = 0$. $H$ est le milieu du segment $[CD]$ donc $H$ a pour coordonnées $\left(0;2\sqrt{3};\sqrt{6}\right)$.
- Démontrer que le milieu J de [BD] est le point d'intersection de la droite (BD) et du plan $\mathcal{P}$. $J$ est le milieu de $[BD]$. Ses coordonnées sont donc $\left(1,5;0,5\sqrt{3};\sqrt{6}\right)$.
- Donner une représentation paramétrique de la droite (AD), puis démontrer que le plans $\mathcal{P}$ et la droite (AD) sont sécants en un point K dont on déterminera les coordonnées. On a $\vec{AD}\left(3;\sqrt{3};2\sqrt{6}\right)$.
- Démontrer que les droites (IJ) et (JK) sont perpendiculaires. $\vec{IJ}\left(0;-\sqrt{3};\sqrt{6}\right)$ et $\vec{JK}(-3;0;0)$
- Déterminer précisément la nature de la section du tétraèdre ABCD par le plan $\mathcal{P}$. On appelle $L$ le milieu du segment $[AC]$. Ses coordonnées sont $(-1,5;1,5\sqrt{3};0)$.
Par conséquent $\vec{OH}\left(0;2\sqrt{3};\sqrt{6}\right)$.
Une équation cartésienne du plan $\mathcal{P}$ est de la forme $2\sqrt{3}y+\sqrt{6}z+d=0$.
$I$ est le milieu du segment $[BC]$ donc ses coordonnées sont $\left(1,5;1,5\sqrt{3};0\right)$.
Il appartient au plan $\mathcal{P}$.
Par conséquent $2\sqrt{3}\times 1,5\sqrt{3}+\sqrt{6}\times 0+d=0 \iff 9+d=0 \iff d=-9$
Une équation cartésienne du plan $\mathcal{P}$ est donc $$2y\sqrt{3}+z\sqrt{6}-9=0$$
$\quad$
Regardons si ses coordonnées vérifient l’équation cartésienne du plan $\mathcal{P}$.
$2\sqrt{3}\times 0,5\sqrt{3}+\sqrt{6}\times \sqrt{6}-9=3+6-9=0$.
Donc $J$ appartient bien au plan $\mathcal{P}$.
On a $\vec{BD}\left(-3;\sqrt{3};2\sqrt{6}\right)$.
Une représentation paramétrique de la droite $(BD)$ est donc
$\begin{cases} x=3-3t\\y=t\sqrt{3}\\z=2t\sqrt{6}\end{cases} \quad, t\in \mathbb R$.
Si $t=0,5$ alors $\begin{cases} x=1,5\\y=0,5\sqrt{3}\\z=\sqrt{6}\end{cases}$. On retrouve les coordonnées du point $J$.
Le point $J$ appartient bien également à la droite $(BD)$.
Montrons que les vecteurs $\vec{OH}$ et $\vec{BD}$ ne sont pas orthogonaux (pour montrer que la droite et plan sont sécants).
$\vec{OH}.\vec{BD}=0+2\times 3+2\times 6=18\neq 0$.
Remarque : on pouvait également montrer que le point $B$ n’appartenait pas au plan $\mathcal{P}$ ce qui exclut le fait que la droite soit incluse dans le plan.Par conséquent le point $J$ est le point d’intersection de la droite $(BD)$ et du plan $\mathcal{P}$.
$\quad$
Une représentation paramétrique de la droite $(AD)$ est donc $\begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\end{cases} \quad, k\in \mathbb R$.
Les coordonnées du point d’intersection de la droite $(AD)$ et de plan $\mathcal{P}$ sont solutions du système :
$\begin{align*} \begin{cases}x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\2y\sqrt{3}+z\sqrt{6}-9=0\end{cases} &\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\6k+12k-9=0\end{cases} \\
&\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\18k-9=0\end{cases} \\
&\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\k=0,5\end{cases}\\
&\iff \begin{cases} k=0,5\\x=-1,5\\y=0,5\sqrt{3}\\z=\sqrt{6}\end{cases}\end{align*}$
Le point $K$ a donc pour coordonnées $\left(-1,5;0,5\sqrt{3};\sqrt{6}\right)$.
$K$ est donc le milieu du segment $[AD]$.
$\quad$
Ainsi $\vec{IJ}.\vec{JK}=0+0+0=0$.
Ces deux vecteurs sont orthogonaux. Le point $J$ appartient aux droites $(IJ)$ et $(JK)$.
Ces deux droites dont donc perpendiculaires.
$\quad$
Montrons qu’il appartient au plan $\mathcal{P}$ :
$2\times 1,5\sqrt{3}\times \sqrt{3}+0-9=9-9=0$.
Ainsi $L$ est l’intersection de la droite $(AC)$ et du plan $\mathcal{P}$.
La section du tétraèdre $ABCD$ par le plan $\mathcal{P}$ est donc le quadrilatère $IJKL$.
En utilisant le théorème des milieux dans les triangles $ABC$, $BCD$, $ACD$ et $ABD$ on montre que :
$IL=\dfrac{AB}{2}=3$, $KJ=\dfrac{AB}{2}=3$, $IJ=\dfrac{DC}{2}=3$ et $KL=\dfrac{DC}{2}=3$
$IJKL$ est donc un losange. D’après la question 2.d. il possède un angle droit en $J$. C’est par conséquent un carré.
$\quad$ - Peut-on placer un point M sur l'arête [BD] tel que le triangle OIM soit rectangle en M ? On a $\vec{BD}\left(-3;\sqrt{3};2\sqrt{6}\right)$
$\begin{align*} AD&=\sqrt{3^2+3+4\times 6} \\
&=\sqrt{9+3+24}\\
&=\sqrt{36}\\
&=6
\end{align*}$
$\quad$
On admet pour la suite que toutes les arêtes du solide ABCD ont la même longueur, c'est-à-dire que le tétraèdre ABCD est un tétraèdre
Une représentation paramétrique de la droite $(BD)$ est donc :
$\begin{cases} x=3-3t\\y=t\sqrt{3}\\z=2t\sqrt{6}\end{cases} \quad ,t\in \mathbb R$.
Ainsi $\vec{OM}\left(3-3t;t\sqrt{3};2t\sqrt{6}\right)$ et $\vec{IM}\left(1,5-3t;t\sqrt{3}-1,5\sqrt{3};2t\sqrt{6}\right)$.
Le triangle $OIM$ est rectangle en $M$
$\iff \vec{OM}.\vec{IM}=0$
$\iff (1,5-3t)(3-3t)+3t^2-4,5t+24t^2=0$
$\iff 4,5-4,5t-9t+9t^2+3t^2-4,5t+24t^2=0$
$\iff 36t^2-18t+4,5=0$
Le discriminant de ce polynôme est $\Delta=-324<0$.
L’équation ne possède pas de solution réelle.
On ne peut donc placer de point $M$ sur l’arête $[BD]$ tel que le triangle $OIM$ soit rectangle en $M$.
$\quad$
Exercice 4 5 points
Dans cet exercice, $x$ et $y$ sont des nombres réels supérieurs à 1.
Dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O}~;~\vec{u},~\vec{v}\right)$, on considère les points A, B et C d'affixes respectives \[z_{\text{A}} = 1 + \text{i}, \: z_{\text{B}} = x + \text{i}\: \text{ et }\: z_{\text{C}} = y + \text{i}.\] 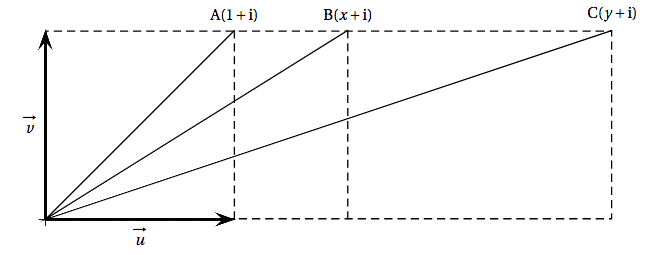
Problème : on cherche les valeurs éventuelles des réels $x$ et $y$, supérieures à 1, pour lesquelles : \[ \text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right).\]
- Démontrer que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$.
- Reproduire sur la copie et compléter l'algorithme ci-après pour qu'il affiche tous les couples $(x,~y)$ tels que : \[\left\{\begin{array}{l} y^2 = 2x^2 + 1 \\ x \text{ et } y \text{ sont des nombres entiers } \\ 1 \leqslant x \leqslant 10 \text{ et } 1 \leqslant y \leqslant 10 \\ \end{array}\right.\] $$\begin{array}{ |l|}\hline \text{ Pour } x \text{ allant de 1 à } \ldots \text{ faire }\\ \hspace{0.5cm} \text{ Pour } \ldots\\ \hspace{1cm} \text{ Si }\ldots\\ \hspace{1.5cm} \text{ Afficher } x \text{ et } y \\ \hspace{1cm} \text{Fin Si}\\ \hspace{0.5cm} \text{Fin Pour}\\ \text{Fin Pour}\\ \hline \end{array}$$ Lorsque l'on exécute cet algorithme, il affiche la valeur $2$ pour la variable $x$ et la valeur $3$ pour la variable $y$.
- Étude d'un cas particulier : dans cette question seulement, on prend $x = 2$ et $y = 3$.
- Donner le module et un argument de $z_{\text{A}}$.
- Montrer que $\text{OC} = \text{OA} \times \text{OB}$.
- Montrer que $z_{\text{B}}z_{\text{C}} = 5 z_{\text{A}}$ et en déduire que $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$.
- On revient au cas général, et on cherche s'il existe d'autres valeurs des réels $x$ et $y$ telles que les points A, B et C vérifient les deux conditions: $\text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$. On rappelle que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$ (question 1.).
- Démontrer que si $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$, alors arg$\left[\dfrac{(x + \text{i})(y + \text{i})}{1 + \text{i}}\right] = 0 \:\text{mod }\: 2\pi$. En déduire que sous cette condition : $x + y - xy + 1 = 0$.
- Démontrer que si les deux conditions sont vérifiées et que de plus $x \neq 1$, alors: \[y= \sqrt{2x^2 + 1}\quad \text{et} \: y = \dfrac{x + 1}{x - 1}.\]
- On définit les fonctions $f$ et $g$ sur l'intervalle $]1~;~+ \infty[$ par : \[f(x) = \sqrt{2x^2 + 1}\quad \text{et} \: g(x) = \dfrac{x + 1}{x - 1}.\] Déterminer le nombre de solutions du problème initial. On pourra utiliser la fonction $h$ définie sur l'intervalle $]1~;~+ \infty[$ par $h(x) = f(x) - g(x)$ et s'appuyer sur la copie d'écran d'un logiciel de calcul formel donnée ci-dessous. $$\begin{array}{|c|}\hline f(x) := \text{sqrt}(2*x\verb+^+2+1) \\ \hline \hspace{1.5cm} x \to \sqrt{2*x^2+1} \\ \hline \text{deriver}(f) \\ \hline \hspace{1.5cm} x \to \dfrac{2*x}{\sqrt{2*x^2+ 1}} \\ \hline g(x) :=(x+1)/(x-1) \\ \hline \hspace{1.5cm} x \to \dfrac{x + 1}{x - 1} \\ \hline \text{deriver}(g) \\ \hline \hspace{1.5cm} x \to - \dfrac{2}{(x - 1)^2} \\ \hline \end{array}$$
Correction de l'exercice 4 5 points
Dans cet exercice, $x$ et $y$ sont des nombres réels supérieurs à 1.
Dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O}~;~\vec{u},~\vec{v}\right)$, on considère les points A, B et C d'affixes respectives \[z_{\text{A}} = 1 + \text{i}, \: z_{\text{B}} = x + \text{i}\: \text{ et }\: z_{\text{C}} = y + \text{i}.\] 
Problème : on cherche les valeurs éventuelles des réels $x$ et $y$, supérieures à 1, pour lesquelles : \[ \text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right).\]
- Démontrer que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$. On a $OC=|y+\text{i}|=\sqrt{y^2+1}$, $OA=|1+\text{i}|=\sqrt{2}$ et $OB=|x+\text{i}|=\sqrt{x^2+1}$.
- Reproduire sur la copie et compléter l'algorithme ci-après pour qu'il affiche tous les couples $(x,~y)$ tels que : \[\left\{\begin{array}{l} y^2 = 2x^2 + 1 \\ x \text{ et } y \text{ sont des nombres entiers } \\ 1 \leqslant x \leqslant 10 \text{ et } 1 \leqslant y \leqslant 10 \\ \end{array}\right.\] $$\begin{array}{ |l|}\hline \text{ Pour } x \text{ allant de 1 à } \ldots \text{ faire }\\ \hspace{0.5cm} \text{ Pour } \ldots\\ \hspace{1cm} \text{ Si }\ldots\\ \hspace{1.5cm} \text{ Afficher } x \text{ et } y \\ \hspace{1cm} \text{Fin Si}\\ \hspace{0.5cm} \text{Fin Pour}\\ \text{Fin Pour}\\ \hline \end{array}$$ Lorsque l'on exécute cet algorithme, il affiche la valeur $2$ pour la variable $x$ et la valeur $3$ pour la variable $y$. On obtient l’algorithme suivant :
- Étude d'un cas particulier : dans cette question seulement, on prend $x = 2$ et $y = 3$.
- Donner le module et un argument de $z_{\text{A}}$. On a $\left|z_A\right|=|1+\text{i}|=\sqrt{2}$
- Montrer que $\text{OC} = \text{OA} \times \text{OB}$. Si $x=2$ et $y=3$.
- Montrer que $z_{\text{B}}z_{\text{C}} = 5 z_{\text{A}}$ et en déduire que $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$. On a :
Donc $z_A=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\right)$ $= \sqrt{2}\left(\cos \left(\dfrac{\pi}{4}\right)+\text{i} \sin \left(\dfrac{\pi}{4}\right)\right)$.
Un argument de $z_A$ est donc $\dfrac{\pi}{4}$.
$\quad$
Alors $OC=\sqrt{3^2+1}=\sqrt{10}$, $OA=\sqrt{2}$ et $\sqrt{OB}=\sqrt{2^2+1}=\sqrt{5}$
Par conséquent $OA\times OB=\sqrt{2}\times \sqrt{5}=\sqrt{10} =OC$.
$\quad$
$\begin{align*}z_Bz_C&=(2+\text{i})(3+\text{i})\\
&=6+2\text{i}+3\text{i}-1\\
&=5+5\text{i}\\
&=5(1+\text{i})\\
&=5z_A
\end{align*}$
Ainsi arg$\left(z_Bz_C\right)=$ arg$\left(z_B\right)+$arg$\left(z_C\right)$ $=\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)$.
arg$\left(5z_A\right)$ $=$arg$\left(z_A\right)=\left(\vec{u},\vec{OA}\right)$.
Donc $\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)=\left(\vec{u},\vec{OA}\right)$
$\quad$ - On revient au cas général, et on cherche s'il existe d'autres valeurs des réels $x$ et $y$ telles que les points A, B et C vérifient les deux conditions: $\text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$. On rappelle que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$ (question 1.).
- Démontrer que si $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$, alors arg$\left[\dfrac{(x + \text{i})(y + \text{i})}{1 + \text{i}}\right] = 0 \:\text{mod }\: 2\pi$. En déduire que sous cette condition : $x + y - xy + 1 = 0$. arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)$
- Démontrer que si les deux conditions sont vérifiées et que de plus $x \neq 1$, alors: \[y= \sqrt{2x^2 + 1}\quad \text{et} \: y = \dfrac{x + 1}{x - 1}.\] Si $OC=OA\times OB$ alors $y^2=2x^2+1$.
$=$ arg $\left((x+\text{i})(y+\text{i})\right)-$ arg$\left(1+\text{i}\right)$
$=$ arg$\left(x+\text{i}\right)+$ arg$\left(y+\text{i}\right)-\left(\vec{u},\vec{OA}\right)$
$=\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)-\left(\vec{u},\vec{OA}\right)$
$=0$ mod $2\pi$
$\quad$
Puisque $y>1$ on a $y=\sqrt{2x^2+1}$
Si $\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)=\left(\vec{u},\vec{OA}\right)$ alors arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)=0$ mod $2\pi$
Or
$\begin{align*} \dfrac{(x+\text{i})(y+\text{i})}{1+\text{i}}&= \dfrac{(x+\text{i})(y+\text{i})}{1+\text{i}}\times \dfrac{1-\text{i}}{1-\text{i}} \\
&=\dfrac{\left(xy+\text{i} x+\text{i} y-1\right)(1-\text{i})}{2} \\
&=\dfrac{\left((xy-1)+\text{i}(x+y)\right)(1-\text{i})}{2}\\
&=\dfrac{(xy-1+x+y)+\text{i}(x+y-xy+1)}{2}
\end{align*}$
Or arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)=0$ mod $2\pi$
$\iff x+y-xy+1=0$
$\iff y(1-x)=-1-x$
$\iff y=\dfrac{x+1}{x-1}$ si $x\neq 1$
$\quad$ - On définit les fonctions $f$ et $g$ sur l'intervalle $]1~;~+ \infty[$ par : \[f(x) = \sqrt{2x^2 + 1}\quad \text{et} \: g(x) = \dfrac{x + 1}{x - 1}.\] Déterminer le nombre de solutions du problème initial. On pourra utiliser la fonction $h$ définie sur l'intervalle $]1~;~+ \infty[$ par $h(x) = f(x) - g(x)$ et s'appuyer sur la copie d'écran d'un logiciel de calcul formel donnée ci-dessous. $$\begin{array}{|c|}\hline f(x) := \text{sqrt}(2*x\verb+^+2+1) \\ \hline \hspace{1.5cm} x \to \sqrt{2*x^2+1} \\ \hline \text{deriver}(f) \\ \hline \hspace{1.5cm} x \to \dfrac{2*x}{\sqrt{2*x^2+ 1}} \\ \hline g(x) :=(x+1)/(x-1) \\ \hline \hspace{1.5cm} x \to \dfrac{x + 1}{x - 1} \\ \hline \text{deriver}(g) \\ \hline \hspace{1.5cm} x \to - \dfrac{2}{(x - 1)^2} \\ \hline \end{array}$$ La fonction $h$ est dérivable sur l’intervalle $]1;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
Ainsi :
$OC=OA\times OB \iff \sqrt{y^2+1}=\sqrt{2}\sqrt{x^2+1}$
Par conséquent $ y^2+1=2x^2+2$ soit $y^2=2x^2+1$
$\quad$
$$\begin{array}{ |l|}\hline \text{ Pour } x \text{ allant de 1 à } 10 \text{ faire }\\ \hspace{0.5cm} \text{ Pour } y \text{ allant de 1 à } 10\\ \hspace{1cm} \text{ Si }y^2=2x^2+1\\ \hspace{1.5cm} \text{ Afficher } x \text{ et } y \\ \hspace{1cm} \text{Fin Si}\\ \hspace{0.5cm} \text{Fin Pour}\\ \text{Fin Pour}\\ \hline \end{array}$$
On a $h'(x)=\dfrac{2x}{\sqrt{2x^2+1}}+\dfrac{2}{(x-1)^2}$.
Puisque $x>1$ cela signifie donc que $h'(x)>0$.
La fonction $h$ est donc strictement croissante sur $]1;+\infty[$.
$\lim\limits_{x \to 1^+}f(x)=\sqrt{3}$
$\lim\limits_{x \to 1^+} x-1=0^+$ et $\lim\limits_{x \to 1^+}x+1=2$ donc $\lim\limits_{x \to 1^+} g(x)=+\infty$.
Par conséquent $\lim\limits_{x \to 1^+} h(x)=-\infty$
$\lim\limits_{x \to +\infty} 2x^2+1=+\infty$ et $\lim\limits_{X \to +\infty} \sqrt{X}=+\infty$ donc $\lim\limits_{x \to +\infty} f(x)=+\infty$
D’après la limite du quotient des termes de plus haut degré on a :
$\lim\limits_{x \to +\infty} h(x)=\lim\limits_{x \to +\infty} \dfrac{x}{x}=1$
Donc $\lim\limits_{x \to +\infty} h(x)=+\infty$
La fonction $h$ est continue (car dérivable) et strictement croissante sur l’intervalle $]1;+\infty[$.
D’après les calculs de limite précédent on est en mesure d’appliquer le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) et l’équation $h(x)=0$ possède une unique solution sur l’intervalle $]1;+\infty[$.
Le problème initial possède donc au plus une solution (il n’y avait pas d’équivalence dans ce qui a été montré dans les questions précédentes).
On a vu à la question 3. que $2$ était une solution du problème.
Le problème initial possède donc exactement une solution.
$\quad$
Spécialité 5 points
On s'intéresse à la figure suivante, dans laquelle $a$, $b$ et $c$ désignent les longueurs des hypoténuses des trois triangles rectangles en O dessinés ci-dessous. 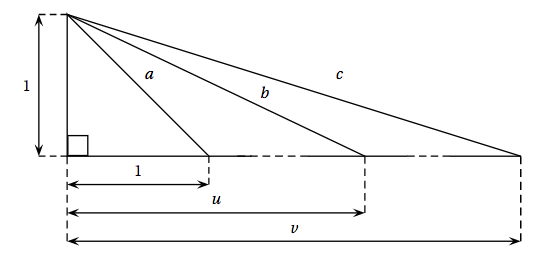
Problème :on cherche les couples de nombres entiers naturels non nuls $(u,~v)$ tels que $ab = c$.
- Modélisation Démontrer que les solutions du problème sont des solutions de l'équation : \[(E) :\quad v^2 - 2u^2 = 1\quad (v \text{ et }\: u \: \text{ étant des entiers naturels non nuls}).\]
- Recherche systématique de solutions de l'équation $(E)$ Recopier et compléter l'algorithme suivant pour qu'il affiche au cours de son exécution tous les couples solutions de l'équation pour lesquels $1 \leqslant u \leqslant 1\;000 $ et $1 \leqslant v \leqslant 1\;000 $. $$\begin{array}{ |l |l| }\hline \text{Pour } u \text{ allant de 1 à } \ldots \text{ faire }& \text{ Au cours de son exécution,}\\ \hspace{0.5cm}\text{Pour } \ldots& \text{ l'algorthme affiche : }\\ \hspace{1cm}\text{ Si }\ldots& 2 \quad 3\\ \hspace{1.5cm}\text{Afficher } u \text{ et } v &12 \quad 17\\ \hspace{1cm}\text{ Fin Si } &70 \quad 99\\ \hspace{0.5cm}\text{ Fin Pour }&408 \quad 577\\ \text{Fin Pour }&\\ \hline \end{array}$$
- Analyse des solutions éventuelles de l'équation $(E)$ On suppose que le couple $(u,~v)$ est une solution de l'équation $(E)$.
- Établir que $u < v$.
- Démontrer que $n$ et $n^2$ ont la même parité pour tout entier naturel $n$.
- Démontrer que $v$ est un nombre impair.
- Établir que $2u^2 =(v-1)(v+1)$. En déduire que $u$ est un nombre pair.
- Une famille de solutions On assimile un couple de nombres entiers $(u,~v)$ à la matrice colonne $X = \begin{pmatrix}u\\v\end{pmatrix}$. On définit également la matrice $A = \begin{pmatrix}3&2\\4&3\end{pmatrix}$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors $AX$ est aussi une solution de l'équation $(E)$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors pour tout entier naturel $n$, $A^n X$ est aussi une solution de l'équation $(E)$.
- À l'aide de la calculatrice, donner un couple $(u,~v)$ solution de l'équation $(E)$ tel que $v > 1\;0000 $.
Correction de l'exercice de Spécialité 5 points
On s'intéresse à la figure suivante, dans laquelle $a$, $b$ et $c$ désignent les longueurs des hypoténuses des trois triangles rectangles en O dessinés ci-dessous. 
Problème :on cherche les couples de nombres entiers naturels non nuls $(u,~v)$ tels que $ab = c$.
- Modélisation : Démontrer que les solutions du problème sont des solutions de l'équation : \[(E) :\quad v^2 - 2u^2 = 1\quad (v \text{ et }\: u \: \text{ étant des entiers naturels non nuls}).\] On applique le théorème de Pythagore dans le triangle rectangle en $O$ d’hypoténuse de longueur $a$.
- Recherche systématique de solutions de l'équation $(E)$ Recopier et compléter l'algorithme suivant pour qu'il affiche au cours de son exécution tous les couples solutions de l'équation pour lesquels $1 \leqslant u \leqslant 1\;000 $ et $1 \leqslant v \leqslant 1\;000 $. $$\begin{array}{ |l |l| }\hline \text{Pour } u \text{ allant de 1 à } \ldots \text{ faire }& \text{ Au cours de son exécution,}\\ \hspace{0.5cm}\text{Pour } \ldots& \text{ l'algorthme affiche : }\\ \hspace{1cm}\text{ Si }\ldots& 2 \quad 3\\ \hspace{1.5cm}\text{Afficher } u \text{ et } v &12 \quad 17\\ \hspace{1cm}\text{ Fin Si } &70 \quad 99\\ \hspace{0.5cm}\text{ Fin Pour }&408 \quad 577\\ \text{Fin Pour }&\\ \hline \end{array}$$ $$\begin{array}{ |l |l| }\hline \text{Pour } u \text{ allant de 1 à } 1~000 \text{ faire }& \text{ Au cours de son exécution,}\\ \hspace{0.5cm}\text{Pour } v \text{ allant de 1 à } 1~000 \text{ faire }& \text{ l'algorthme affiche : }\\ \hspace{1cm}\text{ Si }v^2-2u^2=1& 2 \quad 3\\ \hspace{1.5cm}\text{Afficher } u \text{ et } v &12 \quad 17\\ \hspace{1cm}\text{ Fin Si } &70 \quad 99\\ \hspace{0.5cm}\text{ Fin Pour }&408 \quad 577\\ \text{Fin Pour }&\\ \hline \end{array}$$
- Analyse des solutions éventuelles de l'équation $(E)$ On suppose que le couple $(u,~v)$ est une solution de l'équation $(E)$.
- Établir que $u < v$. Si le couple $(u,v)$ est une solution de l’équation $(E)$ et que $u \geq v$ alors $2u^2>2v^2$.
- Démontrer que $n$ et $n^2$ ont la même parité pour tout entier naturel $n$. Supposons que $n$ soit pair. Il existe alors un entier naturel $k$ tel que $n=2k$.
- Démontrer que $v$ est un nombre impair. On considère un couple solution $(u,v)$ du problème.
- Établir que $2u^2 =(v-1)(v+1)$. En déduire que $u$ est un nombre pair. On a $v^2-2u^2=1 \iff 2u^2=v^2-1 \iff 2u^2=(v-1)(v+1)$.
Ainsi $2u^2 > v^2$ et $v^2-2u^2<0$.
Cela contredit le fait $v^2-2u^2=1$.
Par conséquent $u<v$.
$\quad$
Par conséquent $n^2=(2k)^2=4k^2=2\left(2k^2\right)$ et $n^2$ est pair.
Supposons que $n$ soit impair. Il existe alors une entier naturel $k$ tel que $n=2k+1$.
Alors $n^2=(2k+1)^2=4k^2+4k+1=2\left(2k^2+2k\right)+1$ et $n^2$ est impair.
Donc $n$ et $n^2$ ont la même parité.
$\quad$
Alors $v^2-2u^2=1 \iff v^2=2u^2+1$.
$v^2$ est donc impair. Par conséquent, d’après la question précédente $v$ l’est aussi.
$\quad$
$v$ est impair donc $v-1$ et $v+1$ sont pairs.
Il existe ainsi un entier naturel $k$ tel que $v-1=2k$ et $v+1=2(k+1)$.
Alors $2u^2=2k\times 2(k+1) \iff u^2=2k(k+1)$.
$u^2$ est donc pair.
D’après la question 3.b. $u$ est par conséquent pair.
$\quad$ - Une famille de solutions On assimile un couple de nombres entiers $(u,~v)$ à la matrice colonne $X = \begin{pmatrix}u\\v\end{pmatrix}$. On définit également la matrice $A = \begin{pmatrix}3&2\\4&3\end{pmatrix}$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors $AX$ est aussi une solution de l'équation $(E)$. Soit $X$ est une solution de l’équation $(E)$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors pour tout entier naturel $n$, $A^n X$ est aussi une solution de l'équation $(E)$. Montrons à l’aide d’un raisonnement par récurrence sur $n$ que si une matrice colonne $X$ est une solution de l’équation $(E)$ alors $A^nX$ est aussi une solution de l’équation $(E)$.
- À l'aide de la calculatrice, donner un couple $(u,~v)$ solution de l'équation $(E)$ tel que $v > 1\;0000 $. $3^2-2\times 2^2=9-8=1$.
$AX=\begin{pmatrix} 3u+2v\\4u+3v\end{pmatrix}$.
$\begin{align*} (4u+3v)^2-2(3u+2v)^2&=16u^2+9v^2+24uv-2\left(9u^2+4v^2+12uv\right) \\
&=16u^2+9v^2+24uv-18u^2-8v^2-24uv \\
&=v^2-2u^2\\
&=1
\end{align*}$
$AX$ est donc une solution de l’équation $(E)$.
$\quad$.
On suppose que la matrice colonne $X$ est une solution de l’équation $(E)$
Initialisation : si $n=0$ alors $A^nX=X$ et donc $A^nX$ est une solution de l’équation $(E)$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $A^nX$ est aussi une solution de l’équation $(E)$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $A^{n+1}X$ est une solution de l’équation $(E)$.
$A^{n+1}X=A\left(A^nX\right)$.
$A^nX$ est aussi une solution de l’équation $(E)$ donc d’après la question précédente $A\left(A^nX\right)$ est également une solution de l’équation $(E)$.
la propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent pour tout entier naturel $n$ la matrice colonne $A^nX$ est aussi une solution de l’équation $(E)$.
$\quad$
Le couple $(2;3)$ est une solution de l’équation $(E)$.
On obtient $A^5X=\begin{pmatrix} 13~860\\19~601\end{pmatrix}$.
D’après la question précédente, le couple $(13~860;19~601)$ est solution de l’équation $(E)$ et $v>10~000$.
$\quad$
On obtient alors : $a^2=1^2+1^1=2$.
On faisant de même dans les deux autres triangles rectangles on peut écrire :
$b^2=1^2+u^2=1+u^2$ et $c^2=1^2+v^2=1+v^2$.
$\quad$
Si $ab=c$ alors $a^2b^2=c^2$.
Par conséquent $2\left(1+u^2\right)=1+v^2$
Soit $2+2u^2=1+v^2$
Et donc $v^2-2u^2=1$.
$\quad$
Les solutions du problème sont par conséquent également les solutions $(u,v)$ de l’équation $(E) : v^2-2u^2=1$ où $u$ et $v$ sont des entiers naturels non nuls.
$\quad$
- Vues: 17920
