Baccalauréat S Polynésie 20 juin 2018 - Correction Exercice 1
Correction de l'exercice 1 (5 points)
Rappel de connaissances :
L'intervalle de fluctuation asymptotique au seuil de 95% est donné par la formule \[\left[p- 1,96\dfrac{\sqrt{p(1 - p)}}{\sqrt{n}}~;~p + 1,96\dfrac{\sqrt{p(1 - p)}}{\sqrt{n}}\right]\] où $n$ désigne la taille de l'échantillon et $p$ la proportion des individus possédant le caractère étudié dans cette population. Les conditions de validité de cet intervalle sont les suivantes : \[n \geqslant 30,\: np \geqslant 5,\: n(1 - p) \geqslant 5.\] La municipalité d'une grande ville dispose d'un stock de DVD qu'elle propose en location aux usagers des différentes médiathèques de cette ville. Afin de renouveler son offre de location, la municipalité décide de retirer des DVD de son stock. Parmi les DVD retirés, certains sont défectueux, d'autres non. Parmi les 6 % de DVD défectueux sur l'ensemble du stock, 98% sont retirés. On admet par ailleurs que parmi les DVD non défectueux, 92% sont maintenus dans le stock; les autres sont retirés.
Les trois parties sont indépendantes.
Partie A
On choisit un DVD au hasard dans le stock de la municipalité. On considère les évènements suivants:
- $D$ :« le DVD est défectueux» ;
- $R$ :« le DVD est retiré du stock» .
On note $\overline{D}$ et $\overline{R}$ les évènements contraires respectifs des évènements $D$ et $R$.
- Démontrer que la probabilité de l'évènement $R$ est $0,134$. On obtient l’arbre pondéré suivant :
- Une association caritative contacte la municipalité dans l'objectif de récupérer l'ensemble des DVD qui sont retirés du stock. Un responsable de la ville affirme alors que parmi ces DVD retirés, plus de la moitié est composée de DVD défectueux. Cette affirmation est-elle vraie ? On veut calculer :
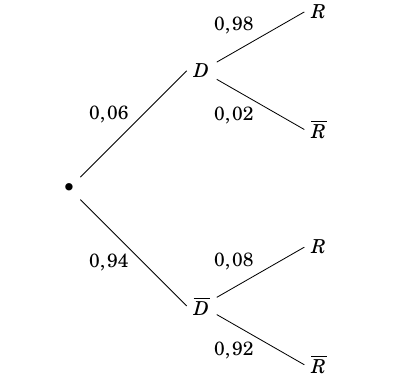
D’après la formule des probabilités totales on a :
$$\begin{align*} p(R) &= p(D\cap R)+p\left(\overline{D}\cap R\right) \\
&=0,06\times 0,98+0,94\times 0,08\\
&=0,134
\end{align*}$$
$\quad$
$\begin{align*} p_R(D)&=\dfrac{p(R\cap D)}{p(R)} \\
&=\dfrac{0,06\times 0,98}{0,134} \\
& \approx 0,44 \\
&<0,5
\end{align*}$
L’affirmation est donc fausse.
$\quad$
Partie B
On a $n=150$ et $p=0,06$.
$n\geq 30$, $np=9 \geq 5$ et $n(1-p)=141 \geq 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion de DVD défectueux est :
$$\begin{align*} I_{150}&=\left[0,06-1,96\sqrt{\dfrac{0,06\times 0,94}{150}};0,06+1,96\sqrt{\dfrac{0,06\times 0,94}{150}}\right] \\
&\approx [0,021;0,099]
\end{align*}$$
La fréquence observée est $f=\dfrac{14}{150}\approx 0,093 \in I_{150}$.
On ne peut donc pas rejeter l’hypothèse faite.
$\quad$
Partie C
Une partie du stock de DVD de la ville est constituée de DVD de films d'animation destinés au jeune public. On choisit un film d'animation au hasard et on note $X$ la variable aléatoire qui donne la durée, en minutes, de ce film. $X$ suit une loi normale d'espérance $\mu = 80$ min et d'écart-type $\sigma$. De plus, on estime que $P(X \geqslant 92) = 0,10$.
- Déterminer le réel $\sigma$ et en donner une valeur approchée à $0,01$. La variable aléatoire $Y=\dfrac{X-\mu}{\sigma}=\dfrac{X-80}{\sigma}$ suit la loi normale centrée réduite.
- Un enfant regarde un film d'animation dont il ne connaît pas la durée. Sachant qu'il en a déjà vu une heure et demie, quelle est la probabilité que le film se termine dans les cinq minutes qui suivent ? L’enfant a déjà vu $1$ h $30$ min du film soit $90$ min.
$$\begin{align*} P(X \geq 92)=0,1 &\iff P(X-80\geq 12)=0,1 \\
&\iff P\left(\dfrac{X-90}{\sigma} \geq \dfrac{12}{\sigma}\right)=0,1 \\
&\iff P\left(\dfrac{X-90}{\sigma} \leq \dfrac{12}{\sigma}\right)=0,9 \\
&\iff P\left(Y \leq \dfrac{12}{\sigma}\right)=0,9 \\
\end{align*}$$
À l’aide de la fonction inverse loi normale de la calculatrice, on trouve :
$\dfrac{12}{\sigma} \approx 1,282$ donc $\sigma \approx 9,36$.
$\quad$
S’il se termine dans les cinq minutes qui suivent cela signifie qu’il dure donc moins de $95$ min.
On veut calculer :
$\begin{align*} P_{X \geq 90}(X \leq 95)&=\dfrac{P(90\leq X\leq 95)}{P(X \geq 90)} \\
&=\dfrac{P(90 \leq X \leq 95)}{0,5-P(80\leq X \leq 90)}\\
&\approx 0,62
\end{align*}$
La probabilité que le film se termine dans les cinq minutes qui suivent sachant qu’il en a déjà vu une heure et demie est environ égale à $62\%$.
$\quad$
- Vues: 16412
