Baccalauréat S Polynésie 20 juin 2018 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

Dans cet exercice, on s'intéresse au volume d'une ampoule basse consommation.

Partie A - Modélisation de la forme de l'ampoule

Le plan est muni d'un repère orthonormé$\left(\text{O}~;~\vec{\imath},~\vec{\jmath}\right)$. On considère les points A$(-1~;~1)$, B$(0~;~1)$, C$(4~;~3)$, D$(7~;~0)$, E$(4~;~-3)$, F$(O~;~-1)$ et G$(- 1~;~- 1)$. On modélise la section de l'ampoule par un plan passant par son axe de révolution à l'aide de la figure ci-dessous :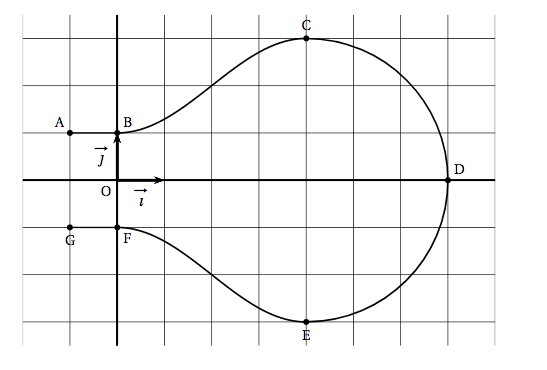

La partie de la courbe située au-dessus de l'axe des abscisses se décompose de la manière suivante:

• la portion située entre les points A et B est la représentation graphique de la fonction constante $h$ définie sur l'intervalle $[-1~;~0]$ par $h(x) = 1$ ;
• la portion située entre les points B et C est la représentation graphique d'une fonction $f$ définie sur l'intervalle $[0~;~4]$ par $f(x) = a + b \sin \left(c + \frac{\pi}{4} x\right)$, où $a$, $b$ et $c$ sont des réels non nuls fixés et où le réel $c$ appartient à l'intervalle $\left[0~;~\frac{\pi}{2}\right]$ ;
• la portion située entre les points C et D est un quart de cercle de diamètre [CE].

La partie de la courbe située en-dessous de l'axe des abscisses est obtenue par symétrie par rapport à l'axe des abscisses.

1. 1. On appelle $f'$ la fonction dérivée de la fonction $f$. Pour tout réel $x$ de l'intervalle $[0~;~4]$, déterminer $f'(x)$.
   La fonction $f$ est dérivable sur l’intervalle $[0;4]$  en tant que somme et composée de fonctions dérivables sur cet intervalle.
   $$f'(x)=b \times \dfrac{\pi}{4}\cos\left(c+\dfrac{\pi}{4}x\right)$$
   $\quad$
   
   2. On impose que les tangentes aux points B et C à la représentation graphique de la fonction $f$ soient parallèles à l'axe des abscisses. Déterminer la valeur du réel $c$.
   La tangente en $B$ est parallèle à l’axe des abscisses donc $f'(0)=0$. Par conséquent $f'(0)=b \times \dfrac{\pi}{4}\cos(c)=0$
   Cela signifie que $c=\dfrac{\pi}{2}+k\pi$.
   On sait que $c$ appartient à l’intervalle $\left[0;\dfrac{\pi}{2}\right]$ donc $c=\dfrac{\pi}{2}$.
   $\quad$
2. Déterminer les réels $a$ et $b$.
On a ainsi $f(x)=a+b\sin\left(\dfrac{\pi}{2}+\dfrac{\pi}{4}x\right)$.
On sait que $f(0)=1$ donc $a+b=1$
et que $f(4)=3$ soit $a+b\sin\left(\dfrac{\pi}{2}+\pi\right)=3\iff a-b=3$.
On résout donc le système suivant :
$\begin{align*} \begin{cases} a+b=1\\a-b=3 \end{cases} &\iff \begin{cases} a=1-b\\1-b-b=3\end{cases} \\
&\iff \begin{cases} a=1-b\\-2b=2 \end{cases} \\
&\iff \begin{cases} b=-1\\a=2\end{cases} \end{align*}$
$\quad$

 

Partie B - Approximation du volume de l'ampoule

Par rotation de la figure précédente autour de l'axe des abscisses, on obtient un modèle de l'ampoule. Afin d'en calculer le volume, on la décompose en trois parties comme illustré ci-dessous: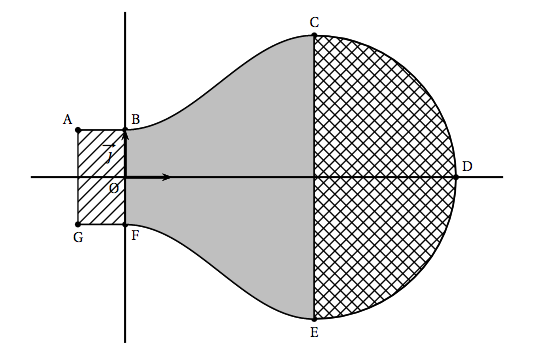

On rappelle que:

• le volume d'un cylindre est donné par la formule $\pi r^2 h$ où $r$ est le rayon du disque de base et $h$ est la hauteur ;
• le volume d'une boule de rayon $r$ est donné par la formule $\dfrac{4}{3}\pi r^3$.

On admet également que, pour tout réel $x$ de l'intervalle $[0~;~4]$, $f(x) = 2 - \cos \left(\frac{\pi}{4}x\right)$.

1. Calculer le volume du cylindre de section le rectangle ABFG.
$OB=1$ est le rayon du cylindre de section le rectangle $ABFG$.
Sa hauteur est $AB=1$.
Le volume de ce cylindre est $V_C=\pi\times OB^2\times AB=\pi$ unité de volume (u.v.).
$\quad$
2. Calculer le volume de la demi-sphère de section le demi -disque de diamètre [CE].
Le rayon de la demi-boule est $R=\dfrac{1}{2}CE=\dfrac{1}{2}\times 6=3$.
Le volume de la demi-boule est :
$\begin{align*} V_B&=\dfrac{1}{2}\times \dfrac{4}{3}\pi R^3 \\
&=\dfrac{2}{3}\pi \times 3^3\\
&=18\pi \text{u.v.}
\end{align*}$
$\quad$
3. Pour approcher le volume du solide de section la zone grisée BCEF, on partage le segment [OO$'$] en $n$ segments de même longueur $\dfrac{4}{n}$ puis on construit $n$ cylindres de même hauteur $\dfrac{4}{n}$.
   1. Cas particulier : dans cette question uniquement on choisit $n = 5$. Calculer le volume du troisième cylindre, grisé dans les figures ci-dessous, puis en donner la valeur arrondie à $10^{-2}$. Figure 3
      
      

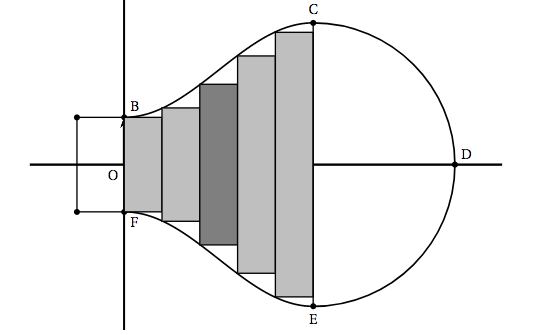
      Vue dans le plan \( (BCE)\).

      
      
      

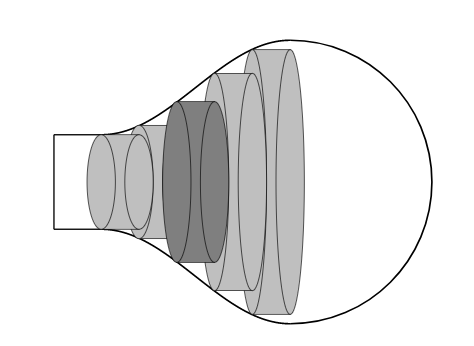
      Vue dans l'espace .

   Le rayon du troisième cylindre est $R_3=f\left(\dfrac{8}{5}\right)$.
   Son volume est donc $V_3=\pi\times \left(f\left(\dfrac{8}{5}\right)\right)^2\times \dfrac{4}{5}=\dfrac{16\pi}{5} \approx 7,19$ u.v. .
   $\quad$
   
   2. Cas général : dans cette question, $n$ désigne un entier naturel quelconque non nul. On approche le volume du solide de section BCEF par la somme des volumes des $n$ cylindres ainsi créés en choisissant une valeur de $n$ suffisamment grande. Recopier et compléter l'algorithme suivant de sorte qu'à la fin de son exécution, la variable $V$ contienne la somme des volumes des $n$ cylindres créés lorsque l'on saisit $n$.
      $$\begin{array}{|ll|}\hline 1& V \gets 0 \\ 2& \text{Pour } k \text{ allant de } \ldots \text{ à } \ldots :\\ 3& \hspace{0.5cm}| V \gets \ldots \\ 4& \text{Fin Pour }\\ \hline \end{array}$$
   On obtient l’algorithme suivant :
   $$\begin{array}{|ll|}\hline 1& V \gets 0 \\ 2& \text{Pour } k \text{ allant de } 0 \text{ à } n-1 :\\ 3& \hspace{0.5cm}| V \gets V+\pi\times \left(2-\cos\left(\dfrac{\pi}{4}\times \dfrac{k*4}{n}\right)\right)^2\times \dfrac{4}{n} \\ 4& \text{Fin Pour }\\ \hline \end{array}$$