Baccalauréat S Amérique du Nord 29 mai 2018 - Correction Exercice 4
Correction de l'exercice 4 5 points
Les deux graphiques donnés en annexe seront à compléter et à rendre avec la copie.
Un scooter radio commandé se déplace en ligne droite à la vitesse constante de 1 m.s$^{-1}$. Il est poursuivi par un chien qui se déplace à la même vitesse. On représente la situation vue de dessus dans un repère orthonormé du plan d'unité 1 mètre. L'origine de ce repère est la position initiale du chien. Le scooter est représenté par un point appartenant à la droite d'équation $x = 5$. Il se déplace sur cette droite dans le sens des ordonnées croissantes.
Dans la suite de l'exercice, on étudie deux modélisations différentes de la trajectoire du chien.
Partie A - Modélisation à l'aide d'une suite
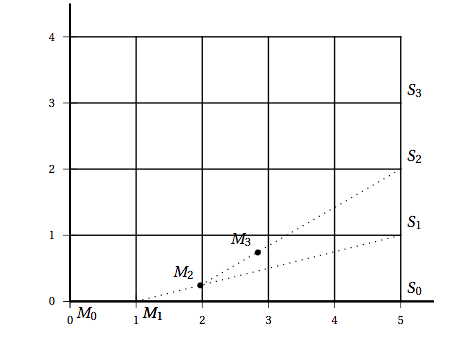
La situation est représentée par le graphique no 1 donné en annexe. À l'instant initial, le scooter est représenté par le point $S_0$. Le chien qui le poursuit est représenté par le point $M_0$. On considère qu'à chaque seconde, le chien s'oriente instantanément en direction du scooter et se déplace en ligne droite sur une distance de 1 mètre. Ainsi, à l'instant initial, le chien s'oriente en direction du point $S_0$, et une seconde plus tard il se trouve un mètre plus loin au point $M_1$. À cet instant, le scooter est au point $S_1$. Le chien s'oriente en direction de $S_1$ et se déplace en ligne droite en parcourant 1 mètre, et ainsi de suite. On modélise alors les trajectoires du chien et du scooter par deux suites de points notées $\left(M_n\right)$ et $\left(S_n\right)$. Au bout de $n$ secondes, les coordonnées du point $S_n$ sont $(5~;~n)$. On note $\left(x_n~;~y_n\right)$ les coordonnées du point $M_n$.
- Construire sur le graphique no 1 donné en annexe les points $M_2$ et $M_3$.
- On note $d_n$ la distance entre le chien et le scooter $n$ secondes après le début de la poursuite. On a donc $d_n = M_nS_n$. Calculer $d_0$ et $d_1$. $d_0=5$
- Justifier que le point $M_2$ a pour coordonnées $\left(1 + \dfrac{4}{\sqrt{17}}~;~\dfrac{1}{\sqrt{17}}\right)$. Déterminons une équation de la droite $\left(M_1S_1\right)$.
- On admet que, pour tout entier naturel $n$ : \[\left\{\begin{array}{l c l} x_{n+1}& = &x_n + \dfrac{5 - x_n}{d_n}\\ y_{n+1}&=&y_n + \dfrac{n - y_n}{d_n} \end{array}\right.\]
- Le tableau ci-dessous, obtenu à l'aide d'un tableur, donne les coordonnées des points $M_n$ et $S_n$ ainsi que la distance $d_n$ en fonction de $n$. Quelles formules doit-on écrire dans les cellules C5 et F5 et recopier vers le bas pour remplir les colonnes C et F ?
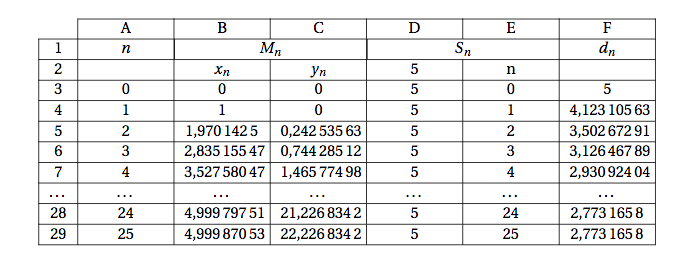 En $C5$ on doit écrire $=C4+(A4-B4)/F4$
En $C5$ on doit écrire $=C4+(A4-B4)/F4$ - On admet que la suite $\left(d_n\right)$ est strictement décroissante. Justifier que cette suite est convergente et conjecturer sa limite à l'aide du tableau. La suite $\left(d_n\right)$ est décroissante et minorée par $0$ (une distance est positive). Cette suite est donc convergente.
En $F5$ on doit écrire $=\text{RACINE}((D5-B5)\hat{~}2+(E5-C5)\hat{~}2)$.
$\quad$
Il semblerait que sa limite soit $2,773~165~8$. - Le tableau ci-dessous, obtenu à l'aide d'un tableur, donne les coordonnées des points $M_n$ et $S_n$ ainsi que la distance $d_n$ en fonction de $n$. Quelles formules doit-on écrire dans les cellules C5 et F5 et recopier vers le bas pour remplir les colonnes C et F ?
$d_1=\sqrt{(5-1)^2+(1-0)^2}=\sqrt{16+1}=\sqrt{17}$
$\quad$
Les points $M_1$ et $S_1$ n’ont pas la même abscisse.
Une équation de cette droite sera donc de la forme $y=ax+b$.
$a=\dfrac{1-0}{5-1}=\dfrac{1}{4}$.
Donc une équation de la droite est de la forme $y=\dfrac{1}{4}x+b$.
Le point $M_1$ de coordonnées $(1;0)$ appartient à la droite.
Ainsi $0=\dfrac{1}{4}+b \iff b=-\dfrac{1}{4}$.
Une équation de la droite $\left(M_1S_1\right)$ est donc $y=\dfrac{1}{4}(x-1)$
Si $x=1+\dfrac{4}{\sqrt{17}}$ alors
$y=\dfrac{1}{4}\times \dfrac{4}{\sqrt{17}}=\dfrac{1}{\sqrt{17}}$.
Le point $A\left(1+\dfrac{4}{\sqrt{17}};\dfrac{1}{\sqrt{17}}\right)$ appartient bien à la droite.
$\quad$
Vérifions que $M_1A=1$.
$M_1A=\sqrt{\left(\dfrac{4}{\sqrt{17}}\right)^2+\left(\dfrac{1}{\sqrt{17}}\right)^2}=\sqrt{\dfrac{16}{17}+\dfrac{1}{17}}=1$.
Le point $M_2$ a donc pour coordonnées $\left(1+\dfrac{4}{\sqrt{17}};\dfrac{1}{\sqrt{17}}\right)$.
Partie B - Modélisation à l'aide d'une fonction
On modélise maintenant la trajectoire du chien à l'aide de la courbe $\mathcal{F}$ de la fonction $f$ définie pour tout réel $x$ de l'intervalle $[0~;~5[$ par: \[f(x) = -2,5\ln (1 - 0, 2x) - 0,5x + 0,05x^2.\]
Cela signifie que le chien se déplace sur la courbe $\mathcal{F}$ de la fonction $f$.
- Lorsque le chien se trouve au point $M$ de coordonnées $(x~;~f(x))$ de la courbe $\mathcal{F}$, où $x$ appartient à l'intervalle $[0~;~5[$, le scooter se trouve au point $S$, d'ordonnée notée $y_S$.
Ainsi le point $S$ a pour coordonnées $\left(5~;~y_S\right)$. La tangente à la courbe $\mathcal{F}$ au point $M$ passe par le point $S$.
Cela traduit le fait que le chien s'oriente toujours en direction du scooter. On note $d(x)$ la distance $MS$ entre le chien et le scooter lorsque $M$ a pour abscisse $x$.- Sur le graphique no 2 donné en annexe, construire, sans calcul, le point $S$ donnant la position du scooter lorsque le chien se trouve au point d'abscisse 3 de la courbe $\mathcal{F}$ et lire les coordonnées du point $S$.
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0~;~5[$ et on admet que, pour tout réel $x$ de l'intervalle $[0~;~5[$ : \[f'(x) = \dfrac{x(1 - 0,1x)}{5 - x}.\] Déterminer par le calcul une valeur approchée au centième de l'ordonnée du point $S$ lorsque le chien se trouve au point d'abscisse 3 de la courbe $\mathcal{F}$. On a $f'(3)=\dfrac{3(1-0,3)}{5-3}=1,05$.
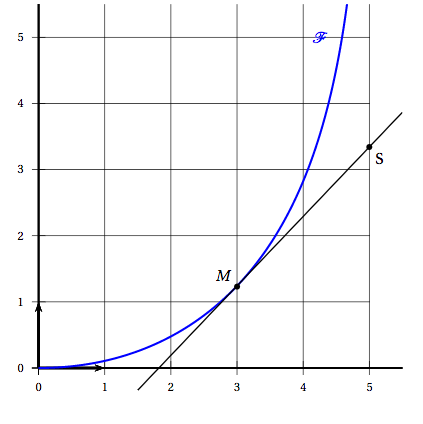 Graphiquement, les coordonnées du point $S$ sont alors $(5;3,3)$.
Graphiquement, les coordonnées du point $S$ sont alors $(5;3,3)$.
$\quad$
Une équation de la tangente en $M$ à la courbe est donc de la forme $y=1,05x+b$.
$f(3)=-2,5\ln(1-0,6)-0,5\times 3+0,05\times 9=-2,5\ln(0,4)-1,05$.
Le point $M$ de coordonnées $\left(3;f(3)\right)$ appartient à la tangente.
Ainsi $-2,5\ln(0,4)-1,05=1,05\times 3+b \iff b=-2,5\ln(0,4)-4,2$.
Une équation de la tangente est donc $y=1,05x-2,5\ln(0,4)-4,2$.
Le point $S$ a pour abscisse $5$.
Son ordonnée est donc $y_S=1,05\times 5-2,5\ln(0,4)-4,2\approx 3,34$.
$\quad$ - On admet que $d(x) = 0,1x^2 - x + 5$ pour tout réel $x$ de l'intervalle $[0~;~5[$. Justifier qu'au cours du temps la distance $MS$ se rapproche d'une valeur limite que l'on déterminera. $\lim\limits_{x \to 5}d(x)=0,1\times 5^2-5+5=2,5$.
Par conséquent la distance $MS$ se rapproche de $2,5$.
$\quad$
- Vues: 20001
