Baccalauréat S Liban 29 mai 2018 - Exercice 4

Page 7 sur 12: Exercice 4

Exercice 4 5 points

Commun à tous les candidats

On considère, pour tout entier $n > 0$, les fonctions $f_n$ définies sur l'intervalle $[1~;~5] $par: \[f_n(x) = \dfrac{\ln x}{x^n}.\] . Pour tout entier $n > 0$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal. Sur le graphique ci-dessous sont représentées les courbes $\mathcal{C}_n$ pour $n$ appartenant à $\{1~;~2~;~3~;~4\}$.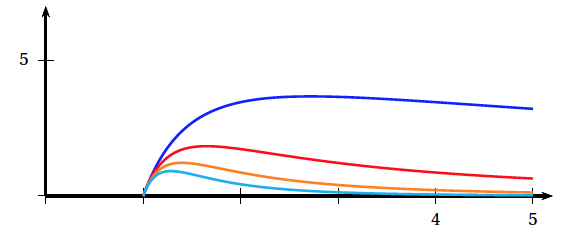

1. Montrer que, pour tout entier $n > 0$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[f'_n(x) = \dfrac{1- n\ln (x)}{x^{n+1}}.\]
2. Pour tout entier $n > 0$, on admet que la fonction $f_n$ admet un maximum sur l'intervalle [1~;~5]. On note $A_n$ le point de la courbe $\mathcal{C}_n$ ayant pour ordonnée ce maximum. Montrer que tous les points $A_n$ appartiennent à une même courbe $\Gamma$ d'équation \[y = \dfrac{1}{\text{e}} \ln (x).\]
3. 1. Montrer que, pour tout entier $n > 1$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[0 \leqslant \dfrac{\ln (x)}{x^n} \leqslant \dfrac{\ln (5)}{x^n}.\]
   2. Montrer que pour tout entier $n > 1$ : \[\displaystyle\int_1^5 \dfrac{1}{x^n} \:\text{d}x = \dfrac{1}{n - 1}\left(1 - \dfrac{1}{5^{n - 1}} \right).\]
   3. Pour tout entier $n > 0$, on s'intéresse à l'aire, exprimée en unités d'aire, de la surface sous la courbe $f_n$, c'est-à-dire l'aire du domaine du plan délimité par les droites d'équations $x = 1$, $x = 5$, $y = 0$ et la courbe $\mathcal{C}_n$. Déterminer la valeur limite de cette aire quand $n$ tend vers $+ \infty$.