Baccalauréat S Amérique du Nord 28 mai 2019

Page 1 sur 10

  

 

Exercice 1 5 points

Commun à tous les candidats

Dans cet exercice et sauf mention contraire, les résultats seront arrondis à $10^{-3}$.
Une usine fabrique des tubes.

Partie A

Les questions 1. et 2 . sont indépendantes.
On s'intéresse à deux types de tubes, appelés tubes de type 1 et tubes de type 2.

1. Un tube de type 1 est accepté au contrôle si son épaisseur est comprise entre $1,35$ millimètre et $1,65$ millimètre.
   1. On désigne par $X$ la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d'une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire $X$ suit la loi normale d'espérance $1,5$ et d'écart-type $0,07$.
      On prélève au hasard un tube de type 1 dans la production de la journée. Calculer la probabilité que le tube soit accepté au contrôle.
   2. L'entreprise désire améliorer la qualité de la production des tubes de type 1. Pour cela, on modifie le réglage des machines produisant ces tubes. On note $X_1$ la variable aléatoire qui, à chaque tube de type 1 prélevé dans la production issue de la machine modifiée, associe son épaisseur. On suppose que la variable aléatoire $X_1$ suit une loi normale d'espérance $1,5$ et d'écart-type $\sigma_1$.
      Un tube de type 1 est prélevé au hasard dans la production issue de la machine modifiée. Déterminer une valeur approchée à $10^{-3}$ près de $\sigma_1$ pour que la probabilité que ce tube soit accepté au contrôle soit égale à 0,98. (On pourra utiliser la variable aléatoire $Z$ définie par $Z = \dfrac{X_1 - 1,5}{\sigma_1}$ qui suit la loi normale centrée réduite.)
2. Une machine produit des tubes de type 2. Un tube de type 2 est dit « conforme pour la longueur » lorsque celle-ci, en millimètres, appartient à l’intervalle $[298~;~302]$. Le cahier des charges établit que, dans la production de tubes de type 2, une proportion de 2% de tubes non « conformes pour la longueur» est acceptable.
   On souhaite décider si la machine de production doit être révisée. Pour cela, on prélève au hasard dans la production de tubes de type 2 un échantillon de $250$ tubes dans lequel 10 tubes se révèlent être non « conformes pour la longueur» .
   1. Donner un intervalle de fluctuation asymptotique à $95$ % de la fréquence des tubes non « conformes pour la longueur» dans un échantillon de $250$ tubes.
   2. Décide-t-on de réviser la machine ? Justifier la réponse.

 

Partie B

Des erreurs de réglage dans la chaine de production peuvent affecter l'épaisseur ou la longueur des tubes de type 2. Une étude menée sur la production a permis de constater que :

• 96% des tubes de type 2 ont une épaisseur conforme;
• parmi les tubes de type 2 qui ont une épaisseur conforme, 95% ont une longueur conforme;
• 3,6% des tubes de type 2 ont une épaisseur non conforme et une longueur conforme.

On choisit un tube de type 2 au hasard dans la production et on considère les événements :

• $E$ : « l'épaisseur du tube est conforme» ;
• $L$ : « la longueur du tube est conforme» .

On modélise l'expérience aléatoire par un arbre pondéré :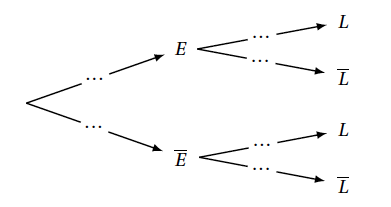

1. Recopier et compléter entièrement cet arbre.
2. Montrer que la probabilité de l'événement $L$ est égale à 0,948.