Baccalauréat S Polynésie 7 juin 2013
Exercice 1 6 points
On considère la fonction $f$ définie sur $\mathbb{R}$ par
\[f(x) = (x + 2)\text{e}^{-x}.\]
On note $\mathscr C$ la courbe représentative de la fonction $f$ dans un repère orthogonal.
- Étude de la fonction $f$.
- Déterminer les coordonnées des points d'intersection de la courbe $\mathscr C$ avec les axes du repère.
- Étudier les limites de la fonction $f$ en $-\infty$ et en $+\infty$. En déduire les éventuelles asymptotes de la courbe $\mathscr C$.
- Étudier les variations de $f$ sur $\mathbb{R}$.
- Calcul d'une valeur approchée de l'aire sous une courbe.
- Dans cette question, on découpe l'intervalle $[0 ; 1]$ en quatre intervalles de même longueur :
- Sur l'intervalle $\left[0 ; \dfrac{1}{4} \right]$, on construit un rectangle de hauteur $f(0)$
- Sur l'intervalle $\left[\dfrac{1}{4} ; \dfrac{1}{2} \right]$, on construit un rectangle de hauteur $f\left( \dfrac{1}{4} \right)$
- Sur l'intervalle $\left[\dfrac{1}{2} ; \dfrac{3}{4} \right]$, on construit un rectangle de hauteur $f\left(\dfrac{1}{2} \right)$
- Sur l'intervalle $\left[ \dfrac{3}{4} ; 1 \right]$, on construit un rectangle de hauteur $f\left( \dfrac{3}{4} \right)$
L'algorithme ci-dessous permet d'obtenir une valeur approchée de l'aire du domaine $\mathscr D$ en ajoutant les aires des quatre rectangles précédents : $$\begin{array}{|rl|} \hline \text{Variables :} & k\; \text{ est un nombre entier} \\ & S \;\text{est un nombre réel} \\ \text{Initialisation : }& \text{Affecter à }S \;\text{la valeur 0 }\\ \text{ Traitement : }& \text{Pour } k \text{ variant de 0 à 3} \\ & \left\vert \text{ Affecter à } S \text{ la valeur } S+\dfrac{1}{4} f\left( \dfrac{k}{4} \right)\right. \\ & \text{Fin Pour} \\ Sortie : & \text{Afficher } S \\ \hline \end{array}$$Donner une valeur approchée à $10^{-3}$ près du résultat affiché par cet algorithme. - Dans cette question, $N$ est un nombre entier strictement supérieur à 1. On découpe l'intervalle $[0 ; 1]$ en $N$ intervalles de même longueur. Sur chacun de ces intervalles, on construit un rectangle en procédant de la même manière qu'à la question 2.a.
Modifier l'algorithme précédent afin qu'il affiche en sortie la somme des aires des $N$ rectangles ainsi construits. - Calcul de la valeur exacte de l'aire sous une courbe.
Soit $g$ la fonction définie sur $\mathbb{R}$ par \[g(x)=(- x - 3) \text{e}^{-x}.\]
On admet que $g$ est une primitive de la fonction $f$ sur $\mathbb{R}$.- Calculer l'aire $\mathscr A$ du domaine $\mathscr D$, exprimée en unités d'aire.
- Donner une valeur approchée à $10^{-3}$ près de l'erreur commise en remplaçant $\mathscr A$ par la valeur approchée trouvée au moyen de l'algorithme de la question 2. a, c'est-à-dire l'écart entre ces deux valeurs.
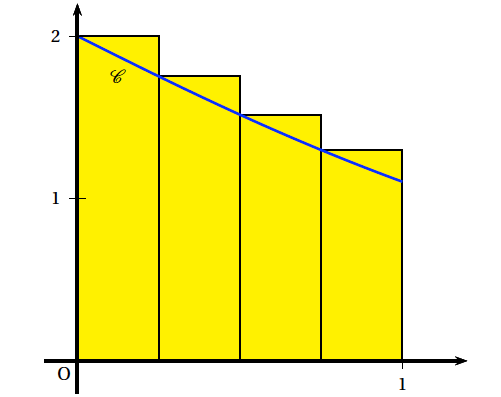
On note $\mathscr D$ le domaine compris entre l'axe des abscisses, la courbe $\mathscr C$ et les droites d'équation $x=0$ et $x=1$. On approche l'aire du domaine $\mathscr D$ en calculant une somme d'aires de rectangles.
Exercice 1 6 points
On considère la fonction $f$ définie sur $\mathbb{R}$ par
\[f(x) = (x + 2)\text{e}^{-x}.\]
On note $\mathscr C$ la courbe représentative de la fonction $f$ dans un repère orthogonal.
- Étude de la fonction $f$.
- Déterminer les coordonnées des points d'intersection de la courbe $\mathscr C$ avec les axes du repère. Points d’intersection avec l’axe des abscisses :
- Étudier les limites de la fonction $f$ en $-\infty$ et en $+\infty$. En déduire les éventuelles asymptotes de la courbe $\mathscr C$. $\left.\begin{array}{l} \lim\limits_{x \to \1}~\2=\3\\ \lim\limits_{x \to \1}~\4=\5 \end{array}\right\}$ par \8 on obtient: $\lim\limits_{x \to \1}~\6=\7$ $~$
- Étudier les variations de $f$ sur $\mathbb{R}$.
- $f'(x)=0 \iff -x-1= 0 \iff x =-1 $
- $ f'(x)>0 \iff -x-1 > 0 \iff - x > -1 \iff x < 1 $
On cherche donc à résoudre:
$$\begin{array}{ll} f(x) = 0 & \Leftrightarrow (x+2)\text{e}^{-x} = 0 \\ & \Leftrightarrow x+2 = 0 \\ & \Leftrightarrow x = -2 \end{array}
$$
Le point d’intersection de $\mathscr{C}$ avec l’axe des abscisses a pour coordonnées $(-2;0)$
$~$
Point d’intersection avec l’axe des ordonnées : $f(0)=2$.
Le point d’intersection avec l’axe des ordonnées a pour coordonnées $(0;2)$.$~$
$f(x) = x\text{e}^{-x} + 2\text{e}^{-x}$.
Par conséquent $\lim\limits_{x \rightarrow + \infty} x\text{e}^{-x} = \lim\limits_{x \rightarrow - \infty}-x\text{e}^x = 0$ et $\lim\limits_{x \rightarrow + \infty} \text{e}^{-x} = 0$ donc $\lim\limits_{x \rightarrow + \infty} f(x) = 0$
Donc la droite déquation $y=0$ est asymptote horizontale à $\mathscr C$ au voisinage de $+\infty$.
$~$
$\1 $ est dérivable comme produit de deux fonctions dérivables :
$\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
$$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$Ainsi :
$$f'(x)=\text{e}^{-x}[1-(x+2)]=\text{e}^{-x}(-1-x)$$ La fonction exponentielle étant strictement positive sur $ \mathbb{R}$, $f'(x)$ a le signe de $-x-1$.
$$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$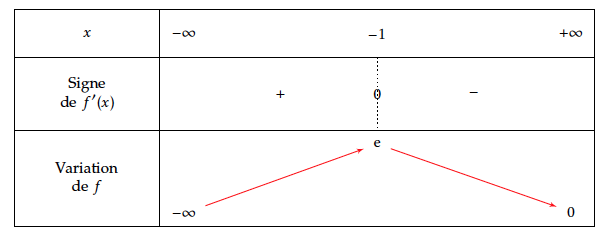
- Calcul d'une valeur approchée de l'aire sous une courbe.
- Dans cette question, on découpe l'intervalle $[0 ; 1]$ en quatre intervalles de même longueur :
- Sur l'intervalle $\left[0 ; \dfrac{1}{4} \right]$, on construit un rectangle de hauteur $f(0)$
- Sur l'intervalle $\left[\dfrac{1}{4} ; \dfrac{1}{2} \right]$, on construit un rectangle de hauteur $f\left( \dfrac{1}{4} \right)$
- Sur l'intervalle $\left[\dfrac{1}{2} ; \dfrac{3}{4} \right]$, on construit un rectangle de hauteur $f\left(\dfrac{1}{2} \right)$
- Sur l'intervalle $\left[ \dfrac{3}{4} ; 1 \right]$, on construit un rectangle de hauteur $f\left( \dfrac{3}{4} \right)$

L'algorithme ci-dessous permet d'obtenir une valeur approchée de l'aire du domaine $\mathscr D$ en ajoutant les aires des quatre rectangles précédents : $$\begin{array}{|rl|} \hline \text{Variables :} & k\; \text{ est un nombre entier} \\ & S \;\text{est un nombre réel} \\ \text{Initialisation : }& \text{Affecter à }S \;\text{la valeur 0 }\\ \text{ Traitement : }& \text{Pour } k \text{ variant de 0 à 3} \\ & \left\vert \text{ Affecter à } S \text{ la valeur } S+\dfrac{1}{4} f\left( \dfrac{k}{4} \right)\right. \\ & \text{Fin Pour} \\ Sortie : & \text{Afficher } S \\ \hline \end{array}$$Donner une valeur approchée à $10^{-3}$ près du résultat affiché par cet algorithme. On a donc $$\begin{array}{l} S &= \dfrac{1}{4}\left(f(0)+f(\left(\dfrac{1}{4}\right) + f\left(\dfrac{1}{2} \right) + f\left(\dfrac{3}{4} \right) \right) \\ &\approx 1,642 \text{ à} 10^{-3} \text{ près} \end{array} - Dans cette question, $N$ est un nombre entier strictement supérieur à 1. On découpe l'intervalle $[0 ; 1]$ en $N$ intervalles de même longueur. Sur chacun de ces intervalles, on construit un rectangle en procédant de la même manière qu'à la question 2.a.
Modifier l'algorithme précédent afin qu'il affiche en sortie la somme des aires des $N$ rectangles ainsi construits. Chacun des $N$ rectangles a une largeur de $\dfrac{1}{N}$ - Calcul de la valeur exacte de l'aire sous une courbe.
Soit $g$ la fonction définie sur $\mathbb{R}$ par \[g(x)=(- x - 3) \text{e}^{-x}.\]
On admet que $g$ est une primitive de la fonction $f$ sur $\mathbb{R}$.- Calculer l'aire $\mathscr A$ du domaine $\mathscr D$, exprimée en unités d'aire. On a donc :
- Donner une valeur approchée à $10^{-3}$ près de l'erreur commise en remplaçant $\mathscr A$ par la valeur approchée trouvée au moyen de l'algorithme de la question 2. a, c'est-à-dire l'écart entre ces deux valeurs. L’erreur commise est donc : $S – \mathscr{A} \approx 0,114$ à $10^{-3}$ près.
$$ \begin{array}{l} \mathscr{A} &= \int_0^1 f(x) \text{d}x \\ & =g(1) – g(0) \\ &=-4\text{e}^{-1} + 3 \text{ u.a.} \end{array}$$
En vidéo !
On note $\mathscr D$ le domaine compris entre l'axe des abscisses, la courbe $\mathscr C$ et les droites d'équation $x=0$ et $x=1$. On approche l'aire du domaine $\mathscr D$ en calculant une somme d'aires de rectangles.
$$
$$\begin{array}{|rl|} \hline \text{Variables :} & k\; \text{ est un nombre entier} \\ & S \;\text{est un nombre réel} \\ \text{Initialisation : }& \text{Affecter à }S \;\text{la valeur 0 }\\ \text{ Traitement : }& \text{Pour } k \text{ variant de 0 à } N -1\\ & \left\vert \text{ Affecter à } S \text{ la valeur } S+\dfrac{1}{N} f\left( \dfrac{k}{N} \right)\right. \\ & \text{Fin Pour} \\ Sortie : & \text{Afficher } S \\ \hline \end{array}$$
Exercice 2 : 4 points
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des quatre propositions est exacte. Chaque réponse correcte rapporte $1$ point. Une réponse erronée ou une absence de réponse n'ôte pas de point. Le candidat indiquera sur la copie le numéro de la question et la réponse choisie.
- Soit $z_1 = \sqrt{6} \text{e}^{\text{i} \frac{\pi}{4}}$ et $z_2 = \sqrt{2} \text{e}^{-\text{i} \frac{\pi}{3}}$. La forme exponentielle de $\text{i} \dfrac{z_1}{z_2}$ est :
- $\sqrt{3}\text{e}^{\text{i} \frac{19\pi}{12}}$
- $\sqrt{12} \text{e}^{-\text{i} \frac{\pi}{12}}$
- $\sqrt{3}\text{e}^{\text{i} \frac{7\pi}{12}}$
- $\sqrt{3}\text{e}^{\text{i} \frac{13\pi}{12}}$
- L'équation $- z = \overline z$, d'inconnue complexe $z$, admet :
- une solution
- deux solutions
- une infinité de solutions dont les points images dans le plan complexe sont situés sur une droite.
- une infinité de solutions dont les points images dans le plan complexe sont situés sur un cercle.
- Dans un repère de l'espace, on considère les trois points $A(1 ; 2 ; 3)$, $B(-1 ; 5 ; 4)$ et $C(-1 ; 0 ; 4)$. La droite parallèle à la droite $(AB)$ passant par le point $C$ a pour représentation paramétrique :
- $\begin{cases} x = -2t-1 \\ y=3t \\ z=t+4 \end{cases}, t\in \mathbb{R}$
- $\begin{cases} x=-1 \\ y=7t \\ z=7t+4 \end{cases}, t \in \mathbb{R}$
- $\begin{cases} x=-1-2t \\ y=5+3t \\ z=4+t \end{cases}, t \in \mathbb{R}$
- $\begin{cases} x=2t \\ y=-3t \\ z=-t \end{cases}, t \in \mathbb{R}$
- Dans un repère orthonormé de l'espace, on considère le plan $\mathscr P$ passant par le point $D(-1 ; 2 ; 3)$ et de vecteur normal $\vec{n}(3 ; -5 ; 1)$, et la droite $\Delta$ de représentation paramétrique $\begin{cases} x = t - 7 \\ y = t + 3 \\ z = 2t + 5 \end{cases}, t \in \mathbb{R}$.
- La droite $\Delta$ est perpendiculaire au plan $\mathscr P$.
- La droite $\Delta$ est parallèle au plan $\mathscr P$ et n'a pas de point commun avec le plan $\mathscr P$.
- La droite $\Delta$ et le plan $\mathscr P$ sont sécants.
- La droite $\Delta$ est incluse dans le plan $\mathscr P$.
Exercice 2 : 4 points
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des quatre propositions est exacte. Chaque réponse correcte rapporte $1$ point. Une réponse erronée ou une absence de réponse n'ôte pas de point. Le candidat indiquera sur la copie le numéro de la question et la réponse choisie.
- Soit $z_1 = \sqrt{6} \text{e}^{\text{i} \frac{\pi}{4}}$ et $z_2 = \sqrt{2} \text{e}^{-\text{i} \frac{\pi}{3}}$. La forme exponentielle de $\text{i} \dfrac{z_1}{z_2}$ est :
- $\sqrt{3}\text{e}^{\text{i} \frac{19\pi}{12}}$
- $\sqrt{12} \text{e}^{-\text{i} \frac{\pi}{12}}$
- $\sqrt{3}\text{e}^{\text{i} \frac{7\pi}{12}}$
- $\sqrt{3}\text{e}^{\text{i} \frac{13\pi}{12}}$
$\text{i} \dfrac{z_1}{z_2} $ $=\text{e}^{\text{i}\pi/2}\dfrac{\sqrt{6}\text{e}^{\text{i}\pi/4}}{\sqrt{2}\text{e}^{-\text{i}\pi/3}}$ $=\sqrt{3}\text{e}^{\text{i}(\pi/2+\pi/4+\pi/3)}$ $=\sqrt{3}\text{e}^{13\text{i}\pi/12}$ - L'équation $- z = \overline z$, d'inconnue complexe $z$, admet :
- une solution
- deux solutions
- une infinité de solutions dont les points images dans le plan complexe sont situés sur une droite.
- une infinité de solutions dont les points images dans le plan complexe sont situés sur un cercle.
On pose $z=x+iy$ - Dans un repère de l'espace, on considère les trois points $A(1 ; 2 ; 3)$, $B(-1 ; 5 ; 4)$ et $C(-1 ; 0 ; 4)$. La droite parallèle à la droite $(AB)$ passant par le point $C$ a pour représentation paramétrique :
- $\begin{cases} x = -2t-1 \\ y=3t \\ z=t+4 \end{cases}, t\in \mathbb{R}$
- $\begin{cases} x=-1 \\ y=7t \\ z=7t+4 \end{cases}, t \in \mathbb{R}$
- $\begin{cases} x=-1-2t \\ y=5+3t \\ z=4+t \end{cases}, t \in \mathbb{R}$
- $\begin{cases} x=2t \\ y=-3t \\ z=-t \end{cases}, t \in \mathbb{R}$
$\vec{AB}(-2;3;1)$ et $C(-1;0;4)$ - Dans un repère orthonormé de l'espace, on considère le plan $\mathscr P$ passant par le point $D(-1 ; 2 ; 3)$ et de vecteur normal $\vec{n}(3 ; -5 ; 1)$, et la droite $\Delta$ de représentation paramétrique $\begin{cases} x = t - 7 \\ y = t + 3 \\ z = 2t + 5 \end{cases}, t \in \mathbb{R}$.
- La droite $\Delta$ est perpendiculaire au plan $\mathscr P$.
- La droite $\Delta$ est parallèle au plan $\mathscr P$ et n'a pas de point commun avec le plan $\mathscr P$.
- La droite $\Delta$ et le plan $\mathscr P$ sont sécants.
- La droite $\Delta$ est incluse dans le plan $\mathscr P$.
Un vecteur directeur de $\Delta$ est $\vec{u}(1;1;2)$.$\vec{u}.\vec{n} = 1 \times 3 + 1 \times (-5) + 2\times 1 = 0$.
Réponse d
$~$
$$-z=\bar{z} \Leftrightarrow -x-\text{i}y = x – iy \Leftrightarrow x = 0$$
Réponse c
$~$
Une réprésentation paramétrique de cette droite est donc :
$$\begin{cases} x=-1-2t \\ y=0+3t \qquad t \in \mathbb{R} \\ z=4+t \end{cases}$$
Réponse a
$~$
Par conséquent ces $2$ vecteurs sont orthogonaux et $\Delta$ est parallèles à $\mathscr{P}$.
$~$
Une équation cartésienne du plan est de la forme : $$3x-5y+z-d=0$$
Or $D \in \mathscr{P}$ .
Donc $3 \times (-1) – 5 \times 2 + 3 + d = 0$ et $d= 10$.
Une équation de $\mathscr{P}$ est, par conséquent : $$3x-5y+z+10=0$$
Le point de coordonnées (-7;3;5) appartient à $\Delta$.
Regardons si ce point appartient également au plan :
$$3 \times (-7) – 5\times 3 + 5 + 10 = -21 \ne 0$$
Réponse b
$~$
Exercice 3 : 5 points
Les $3$ parties peuvent être traitées de façon indépendante.
Thomas possède un lecteur MP3 sur lequel il a stocké plusieurs milliers de morceaux musicaux.
L'ensemble des morceaux musicaux qu'il possède se divise en trois genres distincts selon la répartition suivante : 30 % de musique classique, 45 % de variété, le reste étant du jazz.
Thomas a utilisé deux qualités d'encodage pour stocker ses morceaux musicaux : un encodage de haute qualité et un encodage standard. On sait que :
- les $\dfrac{5}{6}$ des morceaux de musique classique sont encodés en haute qualité.
- les $\dfrac{5}{9}$ des morceaux de variété sont encodés en qualité standard.
On considérera les évènements suivants :
- $C$ : «Le morceau écouté est un morceau de musique classique » ;
- $V$ : «Le morceau écouté est un morceau de variété »;
- $J$ : «Le morceau écouté est un morceau de jazz » ;
- $H$ :«Le morceau écouté est encodé en haute qualité »;
- $S$ :«Le morceau écouté est encodé en qualité standard ».
Partie 1
Thomas décide d'écouter un morceau au hasard parmi tous les morceaux stockés sur son MP3 en utilisant la fonction «lecture aléatoire ».
On pourra s'aider d'un arbre de probabilités.
- Quelle est la probabilité qu'il s'agisse d'un morceau de musique classique encodé en haute qualité ?
- On sait que $P(H)=\dfrac{13}{20}$.
- Les évènements $C$ et $H$ sont-ils indépendants ?
- Calculer $P(J \cap H)$ et $P_J(H)$.
Partie 2
Pendant un long trajet en train, Thomas écoute, en utilisant la fonction «lecture aléatoire » de son MP3, 60 morceaux de musique.
- Déterminer l'intervalle de fluctuation asymptotique au seuil 95 \% de la proportion de morceaux de musique classique dans un échantillon de taille 60.
- Thomas a comptabilisé qu'il avait écouté 12 morceaux de musique classique pendant son voyage. Peut-on penser que la fonction «lecture aléatoire »{} du lecteur MP3 de Thomas est défectueuse ?
Partie 3
On considère la variable aléatoire $X$ qui, à chaque chanson stocké sur le lecteur MP3, associe sa durée exprimée en secondes et on établit que $X$ suit la loi normale d'espérance $200$ et d'écart-type $20$.
On pourra utiliser le tableau fourni en annexe dans lequel les valeurs sont arrondies au millième le plus proche.
On écoute un morceau musical au hasard.
- Donner une valeur approchée à $10^{-3}$ près de $P(180 \leqslant X \leqslant 220)$.
- Donner une valeur approchée à $10^{-3}$ près de la probabilité que le morceau écouté dure plus de 4 minutes.
Exercice 3 : 5 points
Les $3$ parties peuvent être traitées de façon indépendante.
Thomas possède un lecteur MP3 sur lequel il a stocké plusieurs milliers de morceaux musicaux.
L'ensemble des morceaux musicaux qu'il possède se divise en trois genres distincts selon la répartition suivante : 30 % de musique classique, 45 % de variété, le reste étant du jazz.
Thomas a utilisé deux qualités d'encodage pour stocker ses morceaux musicaux : un encodage de haute qualité et un encodage standard. On sait que :
- les $\dfrac{5}{6}$ des morceaux de musique classique sont encodés en haute qualité.
- les $\dfrac{5}{9}$ des morceaux de variété sont encodés en qualité standard.
On considérera les évènements suivants :
- $C$ : «Le morceau écouté est un morceau de musique classique » ;
- $V$ : «Le morceau écouté est un morceau de variété » ;
- $J$ : «Le morceau écouté est un morceau de jazz » ;
- $H$ :«Le morceau écouté est encodé en haute qualité » ;
- $S$ :«Le morceau écouté est encodé en qualité standard ».
Partie 1
Thomas décide d'écouter un morceau au hasard parmi tous les morceaux stockés sur son MP3 en utilisant la fonction «lecture aléatoire ».
On pourra s'aider d'un arbre de probabilités.
- Quelle est la probabilité qu'il s'agisse d'un morceau de musique classique encodé en haute qualité ?
- On sait que $P(H)=\dfrac{13}{20}$.
- Les évènements $C$ et $H$ sont-ils indépendants ? $p(H) \times p(C) = \dfrac{13}{20} \times 0,3 = 0,195 \ne 0,25$
- Calculer $P(J \cap H)$ et $P_J(H)$. D'après la formule des probabilités totales on a : $p(H) = p(J \cap H) + p(V \cap H) + p(C \cap H)$
Donc les $2$ événements ne sont pas indépendants.
$~$
Donc $p(J \cap H) = \dfrac{13}{20} – \dfrac{4}{9} \times 0,45 – 0,25 = 0,2$.
$~$
Par conséquent $$p_J(H) = \dfrac{p(J \cap H)}{p(J)} = 0,8$$

On a donc $p(C \cap H) = p(C)\times p_C(H)=0,3 \times \dfrac{5}{6} = 0,25$
$~$
Partie 2
Pendant un long trajet en train, Thomas écoute, en utilisant la fonction «lecture aléatoire » de son MP3, 60 morceaux de musique.
- Déterminer l'intervalle de fluctuation asymptotique au seuil 95 \% de la proportion de morceaux de musique classique dans un échantillon de taille 60.
- « \3 » considéré comme succès, de probabilité $p=\4$
- « \5 » considéré comme échec, de probabilité $q=1-p=\6$
- Thomas a comptabilisé qu'il avait écouté 12 morceaux de musique classique pendant son voyage. Peut-on penser que la fonction «lecture aléatoire » du lecteur MP3 de Thomas est défectueuse ? La fréquence observée est donc $\dfrac{12}{60} = 0,2 \in I_{60}$.
On répète $\1$ fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :
Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$ et $\4$ notée $\mathscr{B}(\1;\4)$ .
Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
La lecture aléatoire n’est donc pas défectueuse.
$~$
Partie 3
On considère la variable aléatoire $X$ qui, à chaque chanson stocké sur le lecteur MP3, associe sa durée exprimée en secondes et on établit que $X$ suit la loi normale d'espérance $200$ et d'écart-type $20$.
On pourra utiliser le tableau fourni en annexe dans lequel les valeurs sont arrondies au millième le plus proche.
On écoute un morceau musical au hasard.
- Donner une valeur approchée à $10^{-3}$ près de $P(180 \leqslant X \leqslant 220)$. $P(180 \le X \le 220) = P(X \le 220) – P(X \le 180)$ $ = 0,841 – 0,159 $ $= 0,682$
- Donner une valeur approchée à $10^{-3}$ près de la probabilité que le morceau écouté dure plus de 4 minutes. On cherche donc :
$~$ ou directement avec une calculatrice :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$\begin{array}{l} P(X \ge 240) & = 1 – P( X \le 240) \\ & = 1 – 0,977 \\ & = 0,023 \end{array}$$
$~$ ou directement avec une calculatrice :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Exercice 4 : 5 points
On considère la suite $(u_n)$ définie par $u_0=\dfrac{1}{2}$ et telle que pour tout entier naturel $n$,
\[u_{n+1} = \dfrac{3u_n}{1+2u_n}\]
-
- Calculer $u_1$ et $u_2$.
- Démontrer, par récurrence, que pour tout entier naturel $n$, $0 < u_n$.
- On admet que pour tout entier naturel $n$, $u_n<1$.
- Démontrer que la suite $\left(u_n\right)$ est croissante.
- Démontrer que la suite $\left(u_n\right)$ converge.
- Soit $\left(v_n\right)$ la suite définie, pour tout entier naturel $n$, par $v_n = \dfrac{u_n}{1 - u_n}$.
- Montrer que la suite $(v_n)$ est une suite géométrique de raison 3.
- Exprimer pour tout entier naturel $n$, $v_n$ en fonction de $n$.
- En déduire que, pour tout entier naturel $n$, $u_n = \dfrac{3^n}{3^n+1}$.
- Déterminer la limite de la suite $(u_n)$.
Exercice 4 : 5 points
On considère la suite $(u_n)$ définie par $u_0=\dfrac{1}{2}$ et telle que pour tout entier naturel $n$,
\[u_{n+1} = \dfrac{3u_n}{1+2u_n}\]
-
- Calculer $u_1$ et $u_2$.
- Démontrer, par récurrence, que pour tout entier naturel $n$, $0 < u_n$.
- Initialisation : $u_0 = 0,5 > 0$. La propriété est donc vraie au rang $0$
$~$ - Hérédité : Supposons la propriété vraie au rang $n$ : $0 < u_n$.
Alors $u_{n+1} = \dfrac{3u_n}{1+2u_n}$ est un quotient dont le numérateur et le dénominateur sont positifs.
Donc $u_{n+1} > 0$
La propriété est, par conséquent, vraie au rang $n+1$.
$~$ - Conclusion : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang $n+1$.
Par conséquent, pour tout entier naturel $n$, $0< u_n$.$~$
- Initialisation : $u_0 = 0,5 > 0$. La propriété est donc vraie au rang $0$
$u_1 = \dfrac{3u_0}{1+2u_0} = 0,75$ $\quad$ $u_2 = \dfrac{3u_1}{1+2u_1} = 0,9$$~$
- On admet que pour tout entier naturel $n$, $u_n<1$.
- Démontrer que la suite $\left(u_n\right)$ est croissante. $$\begin{array}{l} u_{n+1}-u_{n} &= \dfrac{3u_n}{1+2u_n} – u_n \\ & = \dfrac{3u_n}{1+2u_n} – \dfrac{u_n(1+2u_n)}{1+2u_n} \\ & = \dfrac{3u_n}{1+2u_n} – \dfrac{u_n+2u_n^2}{1+2u_n} \\& = \dfrac{2u_n-2u_n^2}{1+2u_n} \\ & = \dfrac{2u_n(1-u_n)}{1+2u_n} \end{array}$$
- Démontrer que la suite $\left(u_n\right)$ converge.
On sait que $0 < u_n < 1$ donc $\left.\begin{array}{l} 2u_n > 0\\ 1-u_n > 0 \\ 1+2 u_n > 0\end{array}\right\}$ ainsi on a $u_{n+1} – u_n > 0$.
La suite $(u_n)$ est donc strictement croissante.$~$
La suite $(u_n)$ est croissante et majorée par 1; elle est donc convergente.$~$ - Soit $\left(v_n\right)$ la suite définie, pour tout entier naturel $n$, par $v_n = \dfrac{u_n}{1 - u_n}$.
- Montrer que la suite $(v_n)$ est une suite géométrique de raison 3. $$\begin{array} {l}v_{n+1} &= \dfrac{u_{n+1}}{1+u_{n+1}} \\ & = \dfrac{\dfrac{3u_n}{1+2u_n}}{1 +\dfrac{3u_n}{1+2u_n}} \\ &= \dfrac{\dfrac{3u_n}{1+2u_n}}{\dfrac{1+2u_n-3u_n}{1+2u_n}} \\ &=\dfrac{3u_n}{1+2u_n} \times \dfrac{1+2u_n}{1-u_n} \\ &= 3 \dfrac{u_n}{1-u_n} \\ &=3v_n \end{array}$$
- Exprimer pour tout entier naturel $n$, $v_n$ en fonction de $n$.
- En déduire que, pour tout entier naturel $n$, $u_n = \dfrac{3^n}{3^n+1}$. $~$
- Déterminer la limite de la suite $(u_n)$. $\dfrac{1+3^n}{3^n} = \dfrac{1}{3^n} + 1$ donc $\lim\limits_{n \rightarrow + \infty} \dfrac{1}{3^n} = 0$ (car $3 > 1$).
$(v_n)$ est donc une suite géométrique de raison $3$.$~$
Comme $(v_n)$ est une suite géométrique, on a $v_n= q^n \times v_0$.
$v_0 = \dfrac{0,5}{1 – 0,5} = 1$ donc $v_n = 3^n$.
$$ \begin{array} {l} v_n = \dfrac{u_n}{1-u_n}& \Leftrightarrow 3^n = \dfrac{u_n}{1-u_n} \\ &\Leftrightarrow (1-u_n) \times 3^n = u_n \\ & \Leftrightarrow 3^n = u_n + 3^n u_n \\ & \Leftrightarrow u_n = \dfrac{3^n}{1+3^n} \end{array}$$Pour tout entier naturel $n$, $u_n = \dfrac{3^n}{3^n+1}$.
Par conséquent $\lim\limits_{n \rightarrow + \infty} \dfrac{1}{u_n} = \lim\limits_{n \rightarrow + \infty} \dfrac{1 + 3^n}{3^n} = 1$ et $\lim\limits_{n \rightarrow + \infty} u_n = 1$$\lim\limits_{n \rightarrow + \infty} u_n = 1$Remarque : une autre façon consiste à écrire : $$u_n=\dfrac{3^n \times 1}{3^n \times \left (1+ \dfrac{1}{3^n}\right )}=\dfrac{1}{1+\left (\dfrac{1}{3}\right )^n}$$ Comme $-1< \dfrac{1}{3} < 1$, on déduit $\lim\limits_{n \to +\infty}~\left (\dfrac{1}{3}\right )^n=0$ et donc $\lim\limits_{n \to +\infty}~u_n=1.$
Exercice 4 : 5 points
Un opérateur téléphonique A souhaite prévoir l'évolution de nombre de ses abonnés dans une grande ville par rapport à son principal concurrent B à partir de 2013.
En 2013, les opérateurs A et B ont chacun $300$ milliers d'abonnés.
Pour tout entier naturel $n$, on note $a_n$ le nombre d'abonnés, en milliers, de l'opérateur A la $n$-ième année après 2013, et $b_n$ le nombre d'abonnés, en milliers, de l'opérateur B la $n$-ième année après 2013.
Ainsi, $a_0 = 300$ et $b_0 = 300$.
Des observations réalisées les années précédentes conduisent à modéliser la situation par la relation suivante :
pour tout entier naturel $n$, $\begin{cases} a_{n+1} = 0,7a_n + 0,2b_n + 60 \\ b_{n+1} = 0,1a_n + 0,6b_n + 70 \end{cases}$.
On considère les matrices\index{matrice} $M = \begin{pmatrix} 0,7 & 0,2 \\ 0,1 & 0,6 \end{pmatrix}$ et $P = \begin{pmatrix} 60 \\ 70 \end{pmatrix}$.
Pour tout entier naturel $n$, on note $U_n = \begin{pmatrix} a_n \\ b_n \end{pmatrix}$.
-
- Déterminer $U_1$.
- Vérifier que, pour tout entier naturel $n$, $U_{n+1} = M \times U_n +P$.
- On note $I$ la matrice $ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$.
- Calculer $(I - M)\times \begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}$.
- En déduire que la matrice $I - M$ est inversible et préciser son inverse.
- Déterminer la matrice $U$ telle que $U = M \times U + P$.
- Pour tout entier naturel, on pose $V_n = U_n - U$.
- Justifier que, pour tout entier naturel $n$, $V_{n+1} = M \times V_n$.
- En déduire que, pour tout entier naturel $n$, $V_n = M^n \times V_0$.
- On admet que, pour tout entier naturel $n$,
\[V_n = \begin{pmatrix} \dfrac{-100}{3}\times 0,8^n - \dfrac{140}{3} \times 0,5^n \\ \dfrac{-50}{3} \times 0,8^n + \dfrac{140}{3} \times 0,5^n \end{pmatrix}\]
- Pour tout entier naturel $n$, exprimer $U_n$ en fonction de $n$ et en déduire la limite de la suite $(a_n)$.
- Estimer le nombre d'abonnés de l'opérateur A à long terme.
Exercice 4 : 5 points
Un opérateur téléphonique A souhaite prévoir l'évolution de nombre de ses abonnés dans une grande ville par rapport à son principal concurrent B à partir de 2013.
En 2013, les opérateurs A et B ont chacun $300$ milliers d'abonnés.
Pour tout entier naturel $n$, on note $a_n$ le nombre d'abonnés, en milliers, de l'opérateur A la $n$-ième année après 2013, et $b_n$ le nombre d'abonnés, en milliers, de l'opérateur B la $n$-ième année après 2013.
Ainsi, $a_0 = 300$ et $b_0 = 300$.
Des observations réalisées les années précédentes conduisent à modéliser la situation par la relation suivante :
pour tout entier naturel $n$, $\begin{cases} a_{n+1} = 0,7a_n + 0,2b_n + 60 \\ b_{n+1} = 0,1a_n + 0,6b_n + 70 \end{cases}$.
On considère les matrices\index{matrice} $M = \begin{pmatrix} 0,7 & 0,2 \\ 0,1 & 0,6 \end{pmatrix}$ et $P = \begin{pmatrix} 60 \\ 70 \end{pmatrix}$.
Pour tout entier naturel $n$, on note $U_n = \begin{pmatrix} a_n \\ b_n \end{pmatrix}$.
-
- Déterminer $U_1$. $a_1 = 0,7 \times 300 + 0,2 \times 300 + 60 = 330$
- Vérifier que, pour tout entier naturel $n$, $U_{n+1} = M \times U_n +P$. $$ \begin{array}{l} M \times U_n + P &= \begin{pmatrix} 0,7\times a_n + 0,2\times b_n \\\\0,1 \times a_n + 0n6 \times b_n \end{pmatrix} + \begin{pmatrix} 60 \\\\70 \end{pmatrix} \\ &= \begin{pmatrix} 0,7 \times a_n + 0,2\times b_n + 60\\\\0,1 \times a_n + 0,6 \times b_n + 70 \end{pmatrix} \\ &=\begin{pmatrix} a_{n+1}\\\\b_{n+1} \end{pmatrix} \\ &=U_{n+1}
et $b_1 = 0,1 \times 300 + 0,6 \times 300 + 70 = 280$
Donc $U_1 = \begin{pmatrix} 330 \\\\280 \end{pmatrix}$.
$~$
\end{array}$$ - On note $I$ la matrice $ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$.
- Calculer $(I - M)\times \begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}$. $(I – M) = \begin{pmatrix} 0,3&-0,2 \\\\ -0,1&0,4 \end{pmatrix}$
- En déduire que la matrice $I - M$ est inversible et préciser son inverse. Par conséquent $I-M$ est inversible et son inverse est $\begin{pmatrix} 4&2\\\\1&3 \end{pmatrix}$.
- Déterminer la matrice $U$ telle que $U = M \times U + P$. On veut que :
Donc $(I-M) \times \begin{pmatrix} 4&2\\\\1&3 \end{pmatrix} = \begin{pmatrix} 1&0 \\\\0&1 \end{pmatrix} = I$.
$~$
$~$
$$\begin{array} {l}U = M \times U + P & \Leftrightarrow U – M \times U = P \\ & \Leftrightarrow (I-M)U = P \\ &\Leftrightarrow U = (I – M)^{-1} \times P \\ & \Leftrightarrow U = \begin{pmatrix} 380 \\\\270 \end{pmatrix} \end{array}$$ - Pour tout entier naturel, on pose $V_n = U_n - U$.
- Justifier que, pour tout entier naturel $n$, $V_{n+1} = M \times V_n$. $$\begin{array} V_{n+1} &= U_{n+1}-U \\ & = M \times U_n + P -(M \times U + P) \\ &= M \times U_n – M \times U \\ &= M \times (U_n – U) \\ &= M \times V_n \end{array}$$
- En déduire que, pour tout entier naturel $n$, $V_n = M^n \times V_0$. Montrons ce résultat par récurrence.
- Initialisation : $M^0 \times V_0 = I \times V_0 = V_0$.
La propriété est vraie au rang $0$. $~$ - Hérédité : Supposons la propriété vraie au rang $n$ : $V_n = M^n \times V_0$.
Alors $V_{n+1} = M \times V_n = M \times M^n \times V_0 = M^{n+1} \times V_0$.
La propriété est vraie au rang $n+1$. $~$ - Conclusion : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang $n+1$.
Donc pour tout entier naturel $n$, $V_n = M^n \times V_0$.
- On admet que, pour tout entier naturel $n$,
\[V_n = \begin{pmatrix} \dfrac{-100}{3}\times 0,8^n - \dfrac{140}{3} \times 0,5^n \\ \dfrac{-50}{3} \times 0,8^n + \dfrac{140}{3} \times 0,5^n \end{pmatrix}\]
- Pour tout entier naturel $n$, exprimer $U_n$ en fonction de $n$ et en déduire la limite de la suite $(a_n)$. On a donc $$U_n = V_n + U = \begin{pmatrix} \dfrac{-100}{3} \times 0,8^n – \dfrac{140}{3} \times 0,5^n + 380 \\\\ \dfrac{-50}{3} \times 0,8^n + \dfrac{140}{3} \times 0,5^n + 270 \end{pmatrix}$$
- Estimer le nombre d'abonnés de l'opérateur A à long terme.
Par conséquent $a_n = \dfrac{-100}{3} \times 0,8^n – \dfrac{140}{3} \times 0,5^n + 380$.
Or $\lim\limits_{n \rightarrow +\infty} 0,8^n = 0$ car $-1 < 0,8 < 1$
et $\lim\limits_{n \rightarrow +\infty} 0,5^n = 0$ car $-1 < 0,5 < 1$.
Donc $\lim\limits_{n \rightarrow +\infty} a_n = 380$.$~$
A long terme l’opérateur A aura donc $380~000$ abonnés.
$X$ est une variable aléatoire normale d'espérance 200 et d'écart-type 20. $$ \begin{array}{|c|c|}\hline b & P(X \leqslant b) \\\hline 140 & 0,001 \\\hline 150 & 0,006 \\\hline 160 & 0,023 \\\hline 170 & 0,067 \\\hline 180 & 0,159 \\\hline 190 & 0,309 \\\hline 200 & 0,500 \\\hline 210 & 0,691 \\\hline 220 & 0,841 \\\hline 230 & 0,933 \\\hline 240 & 0,977 \\\hline 250 & 0,994 \\\hline 260 & 0,999 \\\hline \end{array}$$
- Vues: 43781
