Baccalauréat S Amérique du Sud 21 novembre 2013
Exercice 1 6 points
Partie A
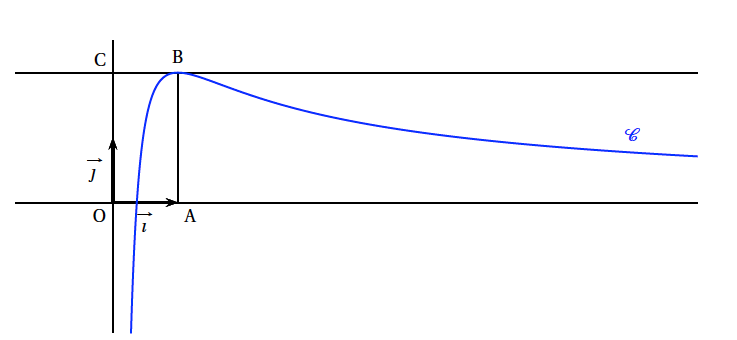
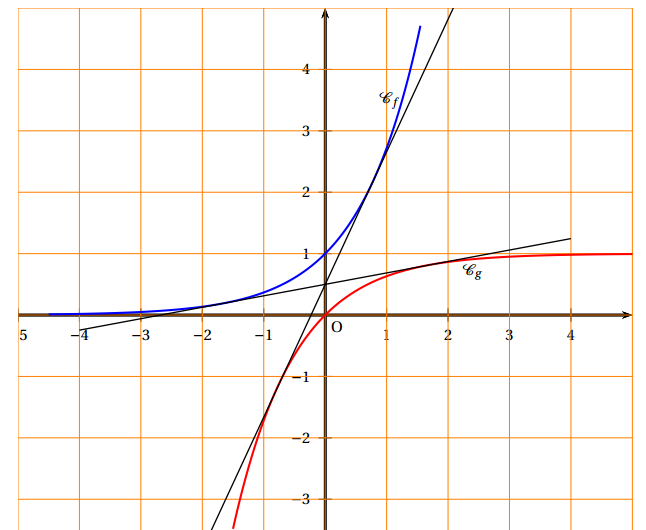
Soit $f$ la fonction définie sur $\mathbb{R}$ par
\[f(x) = x \text{e}^{1-x}.\]
- Vérifier que pour tout réel $x,\: f(x)= \text{e} \times \dfrac{x}{\text{e}^x}$.
- Déterminer la limite de la fonction $f$ en $- \infty$.
- Déterminer la limite de la fonction $f$ en $+ \infty$. Interpréter graphiquement cette limite.
- Déterminer la dérivée de la fonction $f$.
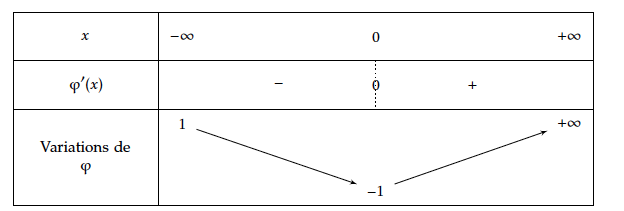
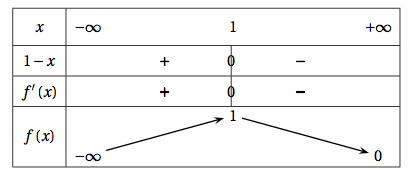
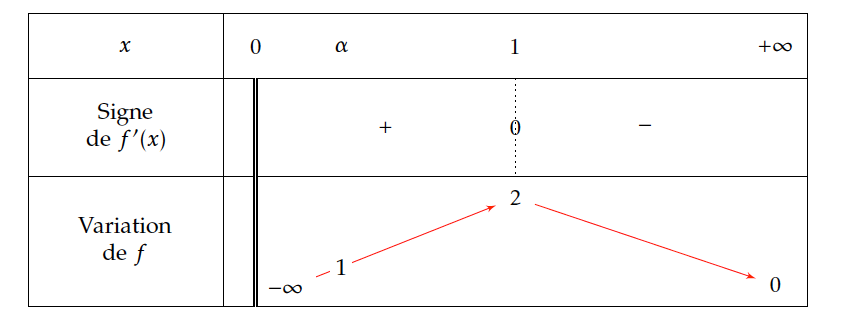
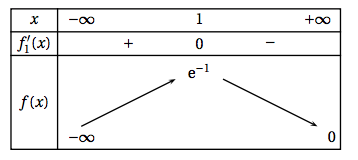
- Étudier les variations de la fonction $f$ sur $\mathbb{R}$ puis dresser le tableau de variation.
Partie B
Pour tout entier naturel $n$ non nul, on considère les fonctions $g_{n}$ et $h_{n}$ définies sur $\mathbb{R}$ par :
\[g_{n}(x) = 1 + x + x^2 + \cdots + x^n \quad \text{et}\quad h_{n}(x) = 1 + 2x + \cdots + nx^{n-1}.\]
- Vérifier que, pour tout réel $x :\: (1 - x)g_{n}(x) = 1 - x^{n+1}$.
On obtient alors, pour tout réel $x \neq 1 :\:\: g_{n}(x) = \dfrac{1 - x^{n+1}}{1 - x}$. - Comparer les fonctions $h_{n}$ et $g'_{n}$, $g'_{n}$ étant la dérivée de la fonction $g_{n}$. En déduire que, pour tout réel $x \neq 1 :\: h_{n}(x) = \dfrac{nx^{n+1} -(n+1)x^n + 1}{(1-x)^2}$.
- Soit $S_{n} = f(1) + f(2) + ... + f(n)$, $f$ étant la fonction définie dans la partie A. En utilisant les résultats de la partie B , déterminer une expression de $S_{n}$ puis sa limite quand $n$ tend vers $+ \infty$.
Partie A
Soit $f$ la fonction définie sur $\mathbb{R}$ par
\[f(x) = x \text{e}^{1-x}.\]
- Vérifier que pour tout réel $x,\: f(x)= \text{e} \times \dfrac{x}{\text{e}^x}$. $f(x)=x\text{e}^{1-x} = x\text{e} \times \text{e}^{-x} = x\text{e} \times \dfrac{1}{\text{e}^x} = \text{e} \times \dfrac{x}{\text{e}}$
- Déterminer la limite de la fonction $f$ en $- \infty$. $\lim\limits_{x \rightarrow -\infty} \dfrac{1}{\text{e}^x} = +\infty$ donc $\lim\limits_{x \rightarrow -\infty} \dfrac{x}{\text{e}^x} = -\infty$ et $\lim\limits_{x \rightarrow -\infty} f(x)=-\infty$
- Déterminer la limite de la fonction $f$ en $+ \infty$. Interpréter graphiquement cette limite. $\lim\limits_{x \rightarrow +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \rightarrow +\infty} \dfrac{x}{\text{e}^x} = 0^+$ et $\lim\limits_{x \rightarrow +\infty} f(x) = 0^+$
- Déterminer la dérivée de la fonction $f$. $f$ est un produit de fonctions dérivables sur $\mathbb R$, par conséquent $f$ est dérivable sur $\mathbb R$.
- Comme $\lim\limits_{x \rightarrow +\infty} f(x) = 0^+$, on déduit que la droite d'équation $y=0$ est asymptote horizontale à $\mathcal{C}_f$ au voisinage de $+\infty$.
- $f'(x) = \text{e}^{1-x} – x\text{e}^{1-x} = (1-x)\text{e}^{1-x}$
- Étudier les variations de la fonction $f$ sur $\mathbb{R}$ puis dresser le tableau de variation. La fonction exponentielle étant toujours positive, le signe de $f'(x)$ ne dépend donc que du signe de $1-x$.
Partie B
Pour tout entier naturel $n$ non nul, on considère les fonctions $g_{n}$ et $h_{n}$ définies sur $\mathbb{R}$ par :
\[g_{n}(x) = 1 + x + x^2 + \cdots + x^n \quad \text{et}\quad h_{n}(x) = 1 + 2x + \cdots + nx^{n-1}.\]
- Vérifier que, pour tout réel $x :\: (1 - x)g_{n}(x) = 1 - x^{n+1}$.
On obtient alors, pour tout réel $x \neq 1 :\:\: g_{n}(x) = \dfrac{1 - x^{n+1}}{1 - x}$.
$(1-x)g_n(x) = 1 +x + x^2 + \ldots+x^n – (x + x^2 + x^3+ \ldots + x^n+x^{n+1}) = 1-x^{n+1}$ (ce sont des sommes télescopiques).
- Comparer les fonctions $h_{n}$ et $g'_{n}$, $g'_{n}$ étant la dérivée de la fonction $g_{n}$. En déduire que, pour tout réel $x \neq 1 :\: h_{n}(x) = \dfrac{nx^{n+1} -(n+1)x^n + 1}{(1-x)^2}$. $ g’_n(x) = 0 + 1 + 2x + 3x^2 + \ldots + nx^{n-1} = h_n(x)$
- Or $g’_n(x) = \dfrac{-(n+1)x^n(1-x)+(1-x^{n+1})}{(1-x)^2}$.
- Soit $S_{n} = f(1) + f(2) + ... + f(n)$, $f$ étant la fonction définie dans la partie A. En utilisant les résultats de la partie B , déterminer une expression de $S_{n}$ puis sa limite quand $n$ tend vers $+ \infty$. $S_n = 1 + 2\text{e}^{-1} + 3\text{e}^{-2}+ \ldots + n\text{e}^{1-n}$
- Donc $h_n(x) = \dfrac{nx^{n+1}-(n+1)x^n+1}{(1-x)^2}$
- $S_n = h_n(\text{e}^{-1}) = \dfrac{n\text{e}^{-n-1}-(n+1)\text{e}^{-n}+1}{(1-\text{e}^{-1})^2}$
- $S_n= \dfrac{\dfrac{n}{\text{e}^{n+1}} – \dfrac{n+1}{\text{e}^{n}}+1}{(1-\text{e}^{-1})^2}$
- $\lim\limits_{n \rightarrow +\infty} \dfrac{n}{\text{e}^n} = 0$ et $\lim\limits_{n \rightarrow +\infty} \dfrac{n+1}{\text{e}^n} = 0$ par conséquent $\lim\limits_{n \rightarrow +\infty} S_n = \dfrac{1}{(1-\text{e}^{-1})^2}$
Exercice 2 4 points
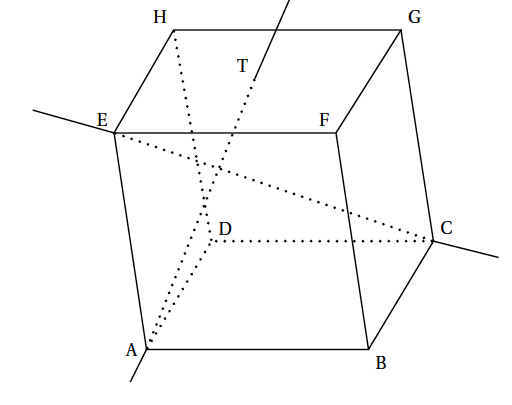
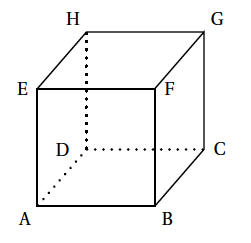
On considère le cube ABCDEFGH, d'arête de longueur 1, représenté ci-dessous et on munit l'espace du repère orthonormé $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$. 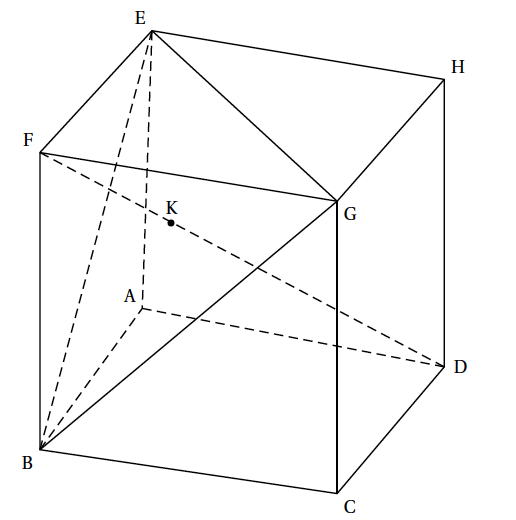
- Déterminer une représentation paramétrique de la droite (FD).
- Démontrer que le vecteur $\vec{n}\begin{pmatrix}1\\- 1\\1\end{pmatrix}$ est un vecteur normal au plan (BGE) et déterminer une équation du plan (BGE).
- Montrer que la droite (FD) est perpendiculaire au plan (BGE) en un point K de coordonnées K$\left(\frac{2}{3} ; \frac{1}{3} ; \frac{2}{3}\right)$.
- Quelle est la nature du triangle BEG ? Déterminer son aire.
- En déduire le volume du tétraèdre BEGD.
Exercice 2 4 points
On considère le cube ABCDEFGH, d'arête de longueur 1, représenté ci-dessous et on munit l'espace du repère orthonormé $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$. 
- Déterminer une représentation paramétrique de la droite (FD). $F(1;0;1)$ et $D(0;1;0)$ donc $\vec{FD}(-1;1;-1)$.
- Démontrer que le vecteur $\vec{n}\begin{pmatrix}1\\- 1\\1\end{pmatrix}$ est un vecteur normal au plan (BGE) et déterminer une équation du plan (BGE). $B(1;0;0)$, $E(0;0;1)$ et $G(1;1;1)$
- Une représentation paramétrique de $(FD)$ est donc $\left\{ \begin{array}{l} x=1-t \\\\y=t\qquad \\\\z=1-t \end{array} \right.$
- Donc $\vec{BG}(0;1;1)$ et $\vec{BE}(-1;0;1)$.
- Ces $2$ vecteurs ne sont pas colinéaires.
- $\vec{n}.\vec{BG} = 0 – 1 + 1 = 0$ et $\vec{n}.\vec{BE} = -1 + 0 + 1 = 0$.
- Par conséquent, $\vec{n}$ est orthogonal à $2$ vecteurs non colinéaires du plan $(BGE)$.
- Il est donc orthogonal au plan.
- Une équation du plan $(BGE)$ est donc de la forme $x-y+z+d=0$.
- $B$ vérifie cette équation. Par conséquent $1+d=0$ et $d=-1$.
- Montrer que la droite (FD) est perpendiculaire au plan (BGE) en un point K de coordonnées K$\left(\frac{2}{3} ; \frac{1}{3} ; \frac{2}{3}\right)$. $\vec{n}=-\vec{FD}$ par conséquent $\vec{FD}$ est orthogonal au plan $(BGE)$ et la droite $(FD)$ est perpendiculaire au plan $(BGE)$.
- Une équation cartésienne de $(BGE)$ est donc $x-y+z-1=0$.
- Recherchons les coordonnées du point d’intersection. Celles-ci vérifient le système d’équations de $(FD)$ ainsi que l’équation de $(BGE)$.
- Donc $1-t-t+1-t-1=0$ soit $t=\dfrac{1}{3}$.
- On obtient donc $x= \dfrac{2}{3}, y = \dfrac{1}{3}$ et $z = \dfrac{2}{3}$.
- Quelle est la nature du triangle BEG ? Déterminer son aire. $[BG]$ , $[BE]$ et $[EG]$ sont des diagonales de carrés de côté $1$.
- $K$ est donc bien le point d’intersection de $(FD)$ et de $(BGE)$.
- Par conséquent $BG = BE = EG = \sqrt{2}$. Le triangle $BEG$ est donc équilatéral.
- Soit $I$ le milieu de $[BE]$ alors, d’après le théorème de Pythagore appliqué dans le triangle rectangle (les médianes sont aussi hauteurs, médiatrices et bissectrices dans un triangle équilatéral) $BGI$ on obtient $GI = \sqrt{\dfrac{3}{2}}$.
- En déduire le volume du tétraèdre BEGD. Le volume du tétraèdre est $\mathcal{V} = \dfrac{\mathcal{A} \times DK}{3}$.
- L’aire du triangle est donc $\mathcal{A} = \dfrac{BE \times GI}{2} = \dfrac{\sqrt{2} \times \sqrt{\dfrac{3}{2}}}{2} = \dfrac{\sqrt{3}}{2}$.
- Or $DK = \sqrt{\dfrac{4}{9} + \dfrac{4}{9} + \dfrac{4}{9}} = \dfrac{2}{\sqrt{3}}$.
- Donc $\mathcal{V} = \dfrac{\dfrac{\sqrt{3}}{2} \times \dfrac{2}{\sqrt{3}}}{3} = \dfrac{1}{3}$
Exercice 3 5 points
Dans cet exercice, les résultats seront arrondis à $10^{-4}$ près.
Partie A
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10 %. L'étude a également permis de prouver que 30 % des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8 % pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements : $M$ : «La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
$C$ : «La personne est victime d'un accident cardiaque au cours de sa vie ».
- Montrer que $P(M \cap C) = 0,03$.
- Calculer $P(C)$.
- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ?
Partie B
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de $400$ personnes, prises au hasard dans la population française. On note $X$ la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
- Définir la loi de la variable aléatoire $X$.
- Déterminer $P(X = 35)$.
- Déterminer la probabilité que $30$ personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme.
Partie C
- On considère la variable aléatoire $F$, définie par $F = \dfrac{X}{400}, X$ étant la variable aléatoire de la Partie B . Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire $F$ au seuil de $95$ %.
- Dans l'échantillon considéré, $60$ personnes présentent une malformation cardiaque de type anévrisme. Qu'en pensez-vous?
Exercice 3 5 points
Dans cet exercice, les résultats seront arrondis à $10^{-4}$ près.
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%.
L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :
$M$ : « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
$C$ : « La personne est victime d'un accident cardiaque au cours de sa vie ».
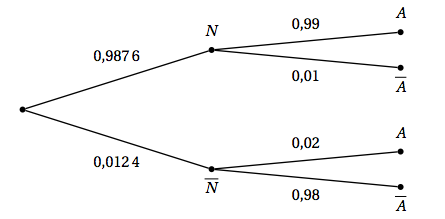
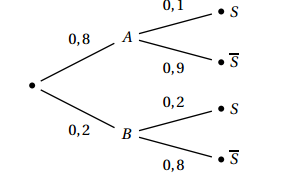
- Faire un arbre pondéré modélisant la situation.
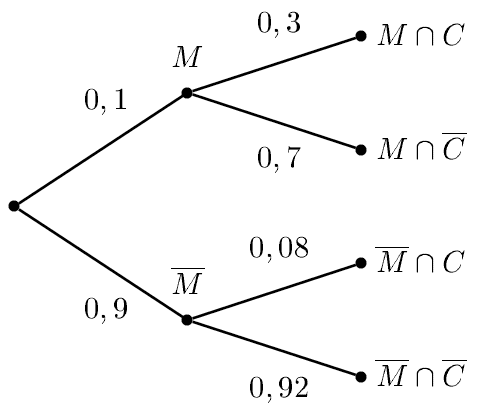
- Montrer que $P(M \cap C) = 0,03$. $$\begin{array}{ll}P(M \cap C)& =P(M)\times P_M(C)\\ &=0,1\times 0,3\\&=0,03\end{array}$$
$$P(M \cap C) = 0,03$$- Calculer $P(C)$. On utilise la partition $\Omega =M\cup \overline{M}$
- on a donc $C =(M\cap C)\cup (\overline{M}\cap C)$ $$\begin{array}{lll}P( C)& =P(M\cap C)+P(\overline{M}\cap C)&\text{ car cette union est disjointe }\\ &= P(M)\times P_M(C)+P(\overline{M})\times P_{\overline{M}}(C)&\\ &=0,1\times 0,3+ 0,9\times 0,08&\\&=0,102&\end{array}$$
$$P( C) = 0,102$$- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ? Ici $C$ est réalisé , on veut donc calculer la probabilité conditionnelle $P_C(M)$ $$\begin{array}{lll}P_C(M) & =\dfrac{P(M\cap C)}{P( C)}&\text{ d'après la définition des probabilités conditionnelles. }\\ &=\dfrac{0,03}{0,102}&\\ &=\dfrac{30}{ 102}= \dfrac{5}{ 17}&\end{array}$$
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de $400$ personnes, prises au hasard dans la population française. On note $X$ la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
- Définir la loi de la variable aléatoire $X$.
- « \3 » considéré comme succès, de probabilité $p=\4$
- « \5 » considéré comme échec, de probabilité $q=1-p=\6$
- Déterminer $P(X = 35)$ et en donner une interprétation.
On répète $\1$ fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :
Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$ et $\4$ notée $\mathscr{B}(\1;\4)$ .
Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$
2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$
- Déterminer la probabilité que $30$ personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme. On veut calculer ici $P(X\geq 30) = 1 -P(X\leq 29)$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
Partie C
- On considère la variable aléatoire $F$, définie par $F = \dfrac{X}{400}, X$ étant la variable aléatoire de la Partie B . Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire $F$ au seuil de $95$ %.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
- Dans l'échantillon considéré, $60$ personnes présentent une malformation cardiaque de type anévrisme. Qu'en pensez-vous? La fréquence observée est donc de $\dfrac{60}{400} = 0,15 \notin I_{400}$.
- $$I_{400} = \left[ 0,1 – 1,96\dfrac{\sqrt{0,1 \times 0,9}}{\sqrt{400}} ; 0,1 + 1,96\dfrac{\sqrt{0,1 \times 0,9}}{\sqrt{400}} \right] = [0,0706;0,1294]$$
- Le nombre de personnes présentant une malformation cardiaque de type anévrisme est donc anormalement élevé.
Exercice 4 5 points
Le plan complexe est rapporté à un repère orthonormé direct. On considère l'équation
\[(E) :\quad z^2 - 2z\sqrt{3} + 4 = 0.\]
- Résoudre l'équation $(E)$ dans l'ensemble $\mathbb{C}$ des nombres complexes.
- On considère la suite $\left(M_{n}\right)$ des points d'affixes $z_{n} = 2^n \text{e}^{\text{i}(- 1)^n\frac{\pi}{6}}$, définie pour $n \geqslant 1$.
- Vérifier que $z_{1}$ est une solution de $(E)$.
- Écrire $z_{2}$ et $z_{3}$ sous forme algébrique.
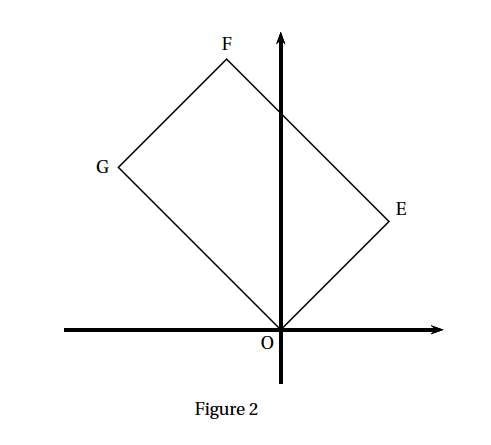
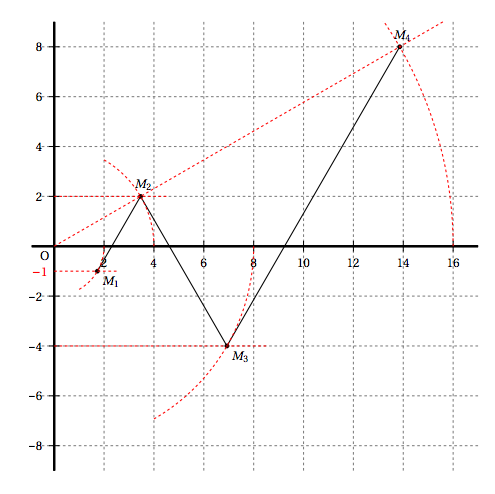
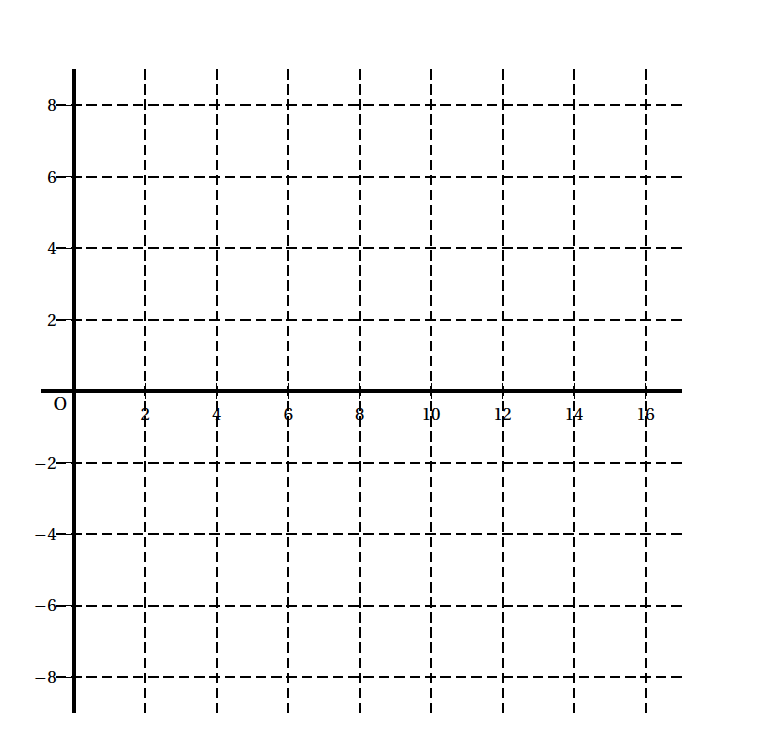
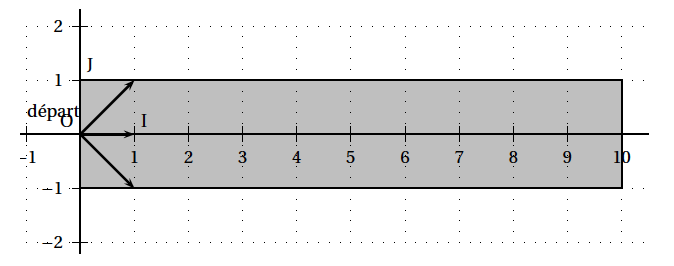
- Placer les points $M_{1},\: M_{2},\: M_{3}$ et $M_{4}$ sur la figure donnée en annexe et tracer, sur la figure donnée en annexe, les segments $\left[M_{1}, M_{2}\right],\: \left[M_{2}, M_{3}\right]$ et $\left[M_{3}, M_{4}\right]$.
- Montrer que, pour tout entier $n \geqslant 1$, $z_{n} = 2^n \left(\dfrac{\sqrt{3}}{2} + \dfrac{(- 1)^n \text{i}}{2}\right)$.
- Calculer les longueurs $M_{1}M_{2}$ et $M_{2}M_{3}$.
- Pour la suite de l'exercice, on admet que, pour tout entier $n \geqslant 1$, $M_{n}M_{n+1} = 2^n \sqrt{3}$.
- On note $\ell_n = M_{1}M_{2} + M_{2}M_{3} + \cdots + M_{n}M_{n+1}$.
- Montrer que, pour tout entier $n \geqslant 1,\; \ell_n = 2\sqrt{3}\left(2^n - 1\right)$.
- Déterminer le plus petit entier $n$ tel que $\ell_n \geqslant 1000 $.
Exercice 4 5 points
Le plan complexe est rapporté à un repère orthonormé direct. On considère l'équation
\[(E) :\quad z^2 - 2z\sqrt{3} + 4 = 0.\]
- Résoudre l'équation $(E)$ dans l'ensemble $\mathbb{C}$ des nombres complexes. $z^2-2z\sqrt{3}+4 = 0$.
- Son discriminant est $\Delta = 4 \times 3 – 16 = -4 < 0$.
- Par conséquent $(E)$ possède $2$ racines complexes :
- On considère la suite $\left(M_{n}\right)$ des points d'affixes $z_{n} = 2^n \text{e}^{\text{i}(- 1)^n\frac{\pi}{6}}$, définie pour $n \geqslant 1$.
- Vérifier que $z_{1}$ est une solution de $(E)$. $z_1 = 2\text{e}^{-\text{i}\pi /6} = 2 \left( \dfrac{\sqrt{3}}{2} – \dfrac{\text{i}}{2} \right) = \sqrt{3} – \text{i}$. Donc $z_1$ est une solution de $(E)$.
- Écrire $z_{2}$ et $z_{3}$ sous forme algébrique. $z_2 = 4\text{e}^{\text{i}\pi /6} = 4 \left(\dfrac{\sqrt{3}}{2} + \dfrac{\text{i}}{2} \right) = 2\sqrt{3} + 2\text{i}$ et $z_3 = 8\text{e}^{-\text{i}\pi/6} = 8 \left(\dfrac{\sqrt{3}}{2} – \dfrac{\text{i}}{2} \right) = 4\sqrt{3} – 4\text{i}$
- Placer les points $M_{1},\: M_{2},\: M_{3}$ et $M_{4}$ sur la figure donnée en annexe et tracer, sur la figure donnée en annexe, les segments $\left[M_{1}, M_{2}\right],\: \left[M_{2}, M_{3}\right]$ et $\left[M_{3}, M_{4}\right]$.
- Montrer que, pour tout entier $n \geqslant 1$, $z_{n} = 2^n \left(\dfrac{\sqrt{3}}{2} + \dfrac{(- 1)^n \text{i}}{2}\right)$. $z_n = 2^n \left( \cos \left( (-1)^n \dfrac{\pi}{6} \right) + \text{i} \sin \left((-1)^n\dfrac{\pi}{6} \right) \right) $
- $$ \dfrac{2\sqrt{3} – 2\text{i}}{2} = \sqrt{3} – \text{i} \quad \text{et} \quad \sqrt{3} + \text{i}$$.
- Calculer les longueurs $M_{1}M_{2}$ et $M_{2}M_{3}$. $M_1M_2 = |z_2 – z_1| = |\sqrt{3} + 3\text{i}| = \sqrt{12} = 2\sqrt{3}$
- $z_n=2^n \left( \cos \left( \dfrac{\pi}{6} \right) + (-1)^n \text{i} \sin \left(\dfrac{\pi}{6} \right) \right) = 2^n \left(\dfrac{\sqrt{3}}{2} + \dfrac{(-1)^n\text{i}}{2} \right)$
- $M_2M_3 = |z_3 – z_2| = |2\sqrt{3} -6\text{i}| = \sqrt{48} = 4\sqrt{3}$
- Pour la suite de l'exercice, on admet que, pour tout entier $n \geqslant 1$, $M_{n}M_{n+1} = 2^n \sqrt{3}$.
- On note $\ell_n = M_{1}M_{2} + M_{2}M_{3} + \cdots + M_{n}M_{n+1}$.
- Montrer que, pour tout entier $n \geqslant 1,\; \ell_n = 2\sqrt{3}\left(2^n - 1\right)$. On a donc :
- $l_n = \sqrt{3}(2 + 2^2 + \ldots + 2^n) = \sqrt{3}(1 + 2 + 2^2 + \ldots + 2^n – 1) = \sqrt{3} \left(\dfrac{1 – 2^{n+1}}{1 – 2} – 1 \right)$.
- $l_n = \sqrt{3}(2^{n+1} – 2) = 2\sqrt{3}(2^n – 1)$.
- Déterminer le plus petit entier $n$ tel que $\ell_n \geqslant 1000 $. On veut que $l_n \ge 1000 \Leftrightarrow 2^n – 1 \ge \dfrac{1000}{2\sqrt{3}} \Leftrightarrow 2^n \ge \dfrac{\sqrt{3} + 500}{\sqrt{3}} \Leftrightarrow n \text{ln }2 \ge \text{ln } \dfrac{\sqrt{3} + 500}{\sqrt{3}}$
- donc $n \ge \dfrac{\text{ln } \dfrac{\sqrt{3} +500}{\sqrt{3}}}{\text{ln }2}$.
- Par conséquent le plus petit entier $n$ tel que $l_n \ge 1000$ est $9$.
Spécialité 5 points
Le gestionnaire d'un site web, composé de trois pages web numérotées de 1 à 3 et reliées entre elles par des liens hypertextes, désire prévoir la fréquence de connexion sur chacune de ses pages web.
Des études statistiques lui ont permis de s'apercevoir que :
- Si un internaute est sur la page no 1, alors il ira, soit sur la page no 2 avec la probabilité $\dfrac{1}{4}$, soit sur la page nosup> 3 avec la probabilité $\dfrac{3}{4}$.
- Si un internaute est sur la page no 2, alors, soit il ira sur la page no 1 avec la probabilité $\dfrac{1}{2}$ soit il restera sur la page no 2 avec la probabilité $\dfrac{1}{4}$, soit il ira sur la page no 3 avec la probabilité $\dfrac{1}{4}$.
- Si un internaute est sur la page no 3, alors, soit il ira sur la page no 1 avec la probabilité $\dfrac{1}{2}$, soit il ira sur la page no 2 avec la probabilité $\dfrac{1}{4}$,soit il restera sur la page no 3 avec la probabilité $\dfrac{1}{4}$.
Pour tout entier naturel $n$, on définit les évènements et les probabilités suivants :
$A_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 1 » et on note $a_{n} = P\left(A_{n}\right)$.
$B_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 2 » et on note $b_{n} = P\left(B_{n}\right)$.
$C_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 3 » et on note $c_{n} = P\left(C_{n}\right)$.
- Montrer que, pour tout entier naturel $n$, on a $a_{n+1} = \dfrac{1}{2} b_{n} + \dfrac{1}{2}c_{n}$.
On admet que, de m\^eme, $b_{n+1} = \dfrac{1}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}$ et $c_{n+1} = \dfrac{3}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}$.
Ainsi :
\[\left\{\begin{array}{l c l} a_{n+1} &=& \dfrac{1}{2} b_{n} + \dfrac{1}{2}c_{n}\\ b_{n+1} &=& \dfrac{1}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}\\ c_{n+1} &=& \dfrac{3}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n} \end{array}\right.\] - Pour tout entier naturel $n$, on pose $U_{n} = \begin{pmatrix} a_{n}\\b_{n}\\c_{n}\end{pmatrix}$.
$U_{0} = \begin{pmatrix} a_{0}\\b_{0}\\c_{0}\end{pmatrix}$ représente la situation initiale, avec $a_{0} + b_{0} + c_{0} = 1$.
Montrer que, pour tout entier naturel $n, U_{n+1} = MU_{n}$ où $M$ est une matrice $3 \times 3$ que l'on précisera.
En déduire que, pour tout entier naturel $n, U_{n} = M^nU_{0}$. - Montrer qu'il existe une seule matrice colonne $U =\begin{pmatrix}x\\y\\z\end{pmatrix}$ telle que : $x + y + z = 1$ et $MU = U$.
- Un logiciel de calcul formel a permis d'obtenir l'expression de $M^n, n$ étant un entier naturel non nul :
\[M^n = \begin{pmatrix} \frac{1}{3} + \frac{\left( \frac{- 1}{2}\right)^n \times 2}{3}&\frac{1}{3} + \frac{\left( \frac{- 1}{2}\right)^n }{- 3}&\frac{1}{3} + \frac{\left(\frac{- 1}{2}\right)^n}{- 3}\\ \frac{1}{4}&\frac{1}{4}&\frac{1}{4}\\ \frac{5}{12} + \frac{\left(-\left(\frac{- 1}{2}\right)^n\right) \times 2}{3}&\frac{5}{12} + \frac{-\left(\frac{- 1}{2}\right)^n}{-3}&\frac{5}{12} + \frac{-\left(\frac{- 1}{2}\right)^n }{- 3} \end{pmatrix}\]
Pour tout entier naturel $n$ non nul, exprimer $a_{n}, b_{n}$ et $c_{n}$ en fonction de $n$. En déduire que les suites $\left(a_{n}\right), \left(b_{n}\right)$ et $\left(c_{n}\right)$ convergent vers des limites que l'on précisera. - Interpréter les résultats obtenus et donner une estimation des pourcentages de fréquentation du site à long terme.
Spécialité 5 points
Le gestionnaire d'un site web, composé de trois pages web numérotées de 1 à 3 et reliées entre elles par des liens hypertextes, désire prévoir la fréquence de connexion sur chacune de ses pages web.
Des études statistiques lui ont permis de s'apercevoir que :
- Si un internaute est sur la page no 1, alors il ira, soit sur la page no 2 avec la probabilité $\dfrac{1}{4}$, soit sur la page nosup> 3 avec la probabilité $\dfrac{3}{4}$.
- Si un internaute est sur la page no 2, alors, soit il ira sur la page no 1 avec la probabilité $\dfrac{1}{2}$ soit il restera sur la page no 2 avec la probabilité $\dfrac{1}{4}$, soit il ira sur la page no 3 avec la probabilité $\dfrac{1}{4}$.
- Si un internaute est sur la page no 3, alors, soit il ira sur la page no 1 avec la probabilité $\dfrac{1}{2}$, soit il ira sur la page no 2 avec la probabilité $\dfrac{1}{4}$,soit il restera sur la page no 3 avec la probabilité $\dfrac{1}{4}$.
Pour tout entier naturel $n$, on définit les évènements et les probabilités suivants :
$A_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 1 » et on note $a_{n} = P\left(A_{n}\right)$.
$B_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 2 » et on note $b_{n} = P\left(B_{n}\right)$.
$C_{n}$ : «Après la $n$-ième navigation, l'internaute est sur la page no 3 » et on note $c_{n} = P\left(C_{n}\right)$.
- Montrer que, pour tout entier naturel $n$, on a $a_{n+1} = \dfrac{1}{2} b_{n} + \dfrac{1}{2}c_{n}$.
On admet que, de m\^eme, $b_{n+1} = \dfrac{1}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}$ et $c_{n+1} = \dfrac{3}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}$.
Ainsi :
\[\left\{\begin{array}{l c l} a_{n+1} &=& \dfrac{1}{2} b_{n} + \dfrac{1}{2}c_{n}\\ b_{n+1} &=& \dfrac{1}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n}\\ c_{n+1} &=& \dfrac{3}{4}a_{n} + \dfrac{1}{4}b_{n} + \dfrac{1}{4}c_{n} \end{array}\right.\]
Après la $(n+1)$-ème navigation, si l’internaute est la page n°$1$, à la $n$-ième navigation il était donc soit sur la page n° $2$ soit sur la page n°$3$.
- Pour tout entier naturel $n$, on pose $U_{n} = \begin{pmatrix} a_{n}\\b_{n}\\c_{n}\end{pmatrix}$.
$U_{0} = \begin{pmatrix} a_{0}\\b_{0}\\c_{0}\end{pmatrix}$ représente la situation initiale, avec $a_{0} + b_{0} + c_{0} = 1$.
Montrer que, pour tout entier naturel $n, U_{n+1} = MU_{n}$ où $M$ est une matrice $3 \times 3$ que l'on précisera.
En déduire que, pour tout entier naturel $n, U_{n} = M^nU_{0}$.
$U_{n+1} = \left(\begin{array}{l} \dfrac{1}{2}b_n+\dfrac{1}{2}c_n \\\\ \dfrac{1}{4}a_n + \dfrac{1}{4}b_n + \dfrac{1}{4}c_n \\\\ \dfrac{3}{4}a_n + \dfrac{1}{4}b_n + \dfrac{1}{4}c_n \end{array} \right)$
- Par conséquent $a_{n+1} = \dfrac{1}{2}b_n + \dfrac{1}{2}c_n$
- $U_{n+1} = \left( \begin{matrix} 0 & \frac{1}{2} & \frac{1}{2} \\\\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\\\ \frac{3}{4} & \frac{1}{4} & \frac{1}{4} \end{matrix} \right) U_n = M\times U_n$ avec $M = \left( \begin{matrix} 0 & \frac{1}{2} & \frac{1}{2} \\\\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\\\ \frac{3}{4} & \frac{1}{4} & \frac{1}{4} \end{matrix} \right)$
- Montrons par récurrence que $U_n = M^nU_0$
Initialisation
- : si $n=0$ alors $U_0 = I U_0$ (où $i$ est la matrice identité).
- La propriété est donc vraie au rang $0$.
Hérédité
- : supposons la propriété vraie au rang $n$ : $U_n = M^nU_0$.
- $U_{n+1} = MU_n = MM^nU_0 = M^{n+1}U_0$.
- La propriété est donc vraie ua rang $n+1$.
Conclusion
- : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang suivant.
- Montrer qu'il existe une seule matrice colonne $U =\begin{pmatrix}x\\y\\z\end{pmatrix}$ telle que : $x + y + z = 1$ et $MU = U$. Soit $U = \left( \begin{matrix} x\\\\ y \\\\ z \end{matrix} \right)$ telle que $x+y+z = 1$ et $U = MU$.
- Par conséquent, pour tout entier naturel $n$, $U_n = M^n U_0$
- $\Leftrightarrow \left\{ \begin{array}{l} x+y+z=1 \\\\x = \frac{1}{2}y + \frac{1}{2}z \\\\y = \frac{1}{4}x + \frac{1}{4}y + \frac{1}{4}z \\\\z = \frac{3}{4}x + \frac{1}{4}y + \frac{1}{4}z \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x+y+z=1 \\\\2x=y+z\\\\4y=x+y+z \\\\4z=3x+y+z\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} z=2x-y \\\\x+y+2x-y = 1\\\\x-3y+2x-y=0 \\\\3x+y-3(2x-y)=0 \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} z=2x-y \\\\3x=1\\\\3x-4y=0 \\\\-3x+4y=0 \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} z=2x-y \\\\x=\dfrac{1}{3}\\\\y = \dfrac{1}{4} \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x=\dfrac{1}{3}\\\\y = \dfrac{1}{4} \\\\ z=\dfrac{5}{12} \end{array} \right.$
- Un logiciel de calcul formel a permis d'obtenir l'expression de $M^n, n$ étant un entier naturel non nul :
\[M^n = \begin{pmatrix} \frac{1}{3} + \frac{\left( \frac{- 1}{2}\right)^n \times 2}{3}&\frac{1}{3} + \frac{\left( \frac{- 1}{2}\right)^n }{- 3}&\frac{1}{3} + \frac{\left(\frac{- 1}{2}\right)^n}{- 3}\\ \frac{1}{4}&\frac{1}{4}&\frac{1}{4}\\ \frac{5}{12} + \frac{\left(-\left(\frac{- 1}{2}\right)^n\right) \times 2}{3}&\frac{5}{12} + \frac{-\left(\frac{- 1}{2}\right)^n}{-3}&\frac{5}{12} + \frac{-\left(\frac{- 1}{2}\right)^n }{- 3} \end{pmatrix}\]
Pour tout entier naturel $n$ non nul, exprimer $a_{n}, b_{n}$ et $c_{n}$ en fonction de $n$. En déduire que les suites $\left(a_{n}\right), \left(b_{n}\right)$ et $\left(c_{n}\right)$ convergent vers des limites que l'on précisera.
$\left\{ \begin{array}{l} a_n = \left( \dfrac{1}{3} + \dfrac{\left( \dfrac{-1}{2} \right)^n \times 2}{3} \right) a_0 + \left( \dfrac{1}{3} + \dfrac{\left( \dfrac{-1}{2} \right)^n }{-3} \right) b_0 + \left( \dfrac{1}{3} + \dfrac{\left( \dfrac{-1}{2} \right)^n }{-3} \right) c_0 \\\\ b_n = \dfrac{1}{4} (a_0 + b_0 + c_0) \\\\ c_n = \left( \dfrac{5}{12} + \dfrac{-\left( \dfrac{-1}{2} \right)^n \times 2}{3} \right) a_0 + \left( \dfrac{5}{12} + \dfrac{\left( \dfrac{-1}{2} \right)^n }{-3} \right) b_0 + \left( \dfrac{5}{12} + \dfrac{-\left( \dfrac{-1}{2} \right)^n }{-3} \right) c_0 \end{array} \right.$
- Il existe donc une seule matrice $U = \left( \begin{matrix} x\\\\ y \\\\ z \end{matrix} \right)$ telle que $x+y+z = 1$ et $U = MU$.
- $\lim\limits_{n \rightarrow + \infty} \left(\dfrac{-1}{2} \right)^n = 0$
- Donc $\lim\limits_{n \rightarrow + \infty} a_n = \dfrac{1}{3}$ , $\lim\limits_{n \rightarrow + \infty} b_n = \dfrac{1}{4}$ et $\lim\limits_{n \rightarrow + \infty} c_n = \dfrac{5}{12}$ (car $a_0 + b_0 + c_0 = 1$).
- Interpréter les résultats obtenus et donner une estimation des pourcentages de fréquentation du site à long terme. Au bout d’un certain temps la page $1$ du site sera consultée $33,33 \%$ du temps, la page $2$ sera consultée $25 \%$ du temps et la page $3$ sera consultée $41,67 \%$ du temps.
- Vues: 47476

 Partie B
Partie B