Baccalauréat S Asie 17 juin 2015

Exercice 1 5 points

Commun à tous les candidats

Les trois parties de cet exercice sont indépendantes. Les probabilités seront arrondies au millième.


Partie A


Un concurrent participe à un concours de tir à l'arc, sur une cible circulaire. À chaque tir, la probabilité qu'il atteigne la cible est égale à $0$,8.

1. Le concurrent tire quatre flèches. On considère que les tirs sont indépendants. Déterminer la probabilité qu'il atteigne au moins trois fois la cible.
2. Combien de flèches le concurrent doit-il prévoir pour atteindre en moyenne la cible douze fois ?



Partie B


Entre deux phases du concours, pour se perfectionner, le concurrent travaille sa précision latérale sur une autre cible d'entraînement, représentée ci-contre. Pour cela, il tire des flèches pour essayer d'atteindre une bande verticale, de largeur $20$ cm (en grisé sur la figure), le plus près possible de la ligne verticale centrale. On munit le plan contenant la bande verticale d'un repère : la ligne centrale visée est l'axe des ordonnées. On note $X$ la variable aléatoire qui, à toute flèche tirée atteignant ce plan, associe l'abscisse de son point d'impact.

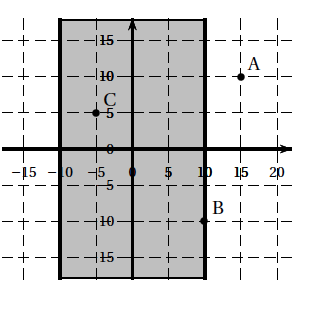
Ainsi, par exemple :
• si la flèche atteint le point A, le tireur a raté la bande, et $X$ prend la valeur $15$ ;
• si elle atteint le point B, l'impact est à la limite de la bande, et $X$ prend la valeur $10$ ;
• si elle atteint le point C, l'impact est dans la bande et $X$ prend la valeur $- 5$.

On suppose que la variable aléatoire $X$ suit une loi normale d'espérance $0$ et d'écart-type $10$.

1. Lorsque la flèche atteint le plan, déterminer la probabilité que son point d'impact soit situé hors de la bande grisée.
2. Comment modifier les bords de la bande grisée pour faire en sorte que, lorsque la flèche atteint le plan, son point d'impact soit situé à l'intérieur de la bande avec une probabilité égale à $0,6$ ?



Partie C


La durée de vie (exprimée en heures) du panneau électrique affichant le score des concurrents est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 10^{-4}$ (exprimé en h$^{-1}$).

1. Quelle est la probabilité que le panneau fonctionne au moins pendant 2000 heures ?
2. Restitution organisée des connaissances
   Dans cette question, $\lambda$ désigne un réel strictement positif. On rappelle que l'espérance mathématique de la variable aléatoire $T$ suivant une loi exponentielle de paramètre $\lambda$, est définie par : E$(T) = \displaystyle\lim_{x \to + \infty} \int_0^x\lambda t \text{e}^{- \lambda t}\text{d}t$.
   1. On considère la fonction $F$, définie pour tout réel $t$ par : $F(t) = \left(- t - \dfrac{1}{\lambda}\right)\text{e}^{- \lambda t}$. Démontrer que la fonction $F$ est une primitive sur $\mathbb R$ de la fonction 1 définie pour tout réel $t$ par : $f(t) = \lambda t\text{e}^{- \lambda t}$.
   2. En déduire que l'espérance mathématique de la variable aléatoire $T$ est égale à $\dfrac{1}{\lambda}$. Quelle est l'espérance de durée de vie du panneau électrique affichant le score des concurrents ?



Correction de l'exercice 1 (5 points)


Commun à tous les candidats

Les trois parties de cet exercice sont indépendantes. Les probabilités seront arrondies au millième.


Partie A


Un concurrent participe à un concours de tir à l'arc, sur une cible circulaire. À chaque tir, la probabilité qu'il atteigne la cible est égale à $0$,8.

1. Le concurrent tire quatre flèches. On considère que les tirs sont indépendants. Déterminer la probabilité qu'il atteigne au moins trois fois la cible.

On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

• « \3 » considéré comme succès, de probabilité $p=\4$
• « \5 » considéré comme échec, de probabilité $q=1-p=\6$

Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

La probabilité qu'il atteigne au moins trois fois la cible est donnée par $P(X\geq 3)= P(X=3)+P(X=4)$.

2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
$P(X\geq 3)= P(X=3)+P(X=4)\approx 0,819$

On peut aussi faire le calcul de cette façon $P(X\geq 3)= 1-P(X\leq 2)$

 

2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
$P(X\geq 3)= 1-P(X\leq 2)\approx 0,8192$ Ou pour terminer

2ND DISTR AbinomFRép( \1 , \2,\5) -2ND DISTR A binomFRép( \1 , \2,\3)EXE


Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\5)-binomFR\text{é}p(\1,\2,\3) \approx \6$$

$$P( \4 \leq \7\leq\5 )\approx \6 \text{ à } 10^{-\8} \text{ près.}$$
2. Combien de flèches le concurrent doit-il prévoir pour atteindre en moyenne la cible douze fois ?
On appelle $X’$ la variable aléatoire comptant le nombre de flèches ayant atteint la cible.
Pour les mêmes raisons qu’à la question précédentes, $X’$ suit la loi binomiale $\mathscr{B}(n;0,8)$.
On veut que :
$$\begin{array}{rl} E(X’) = 12 & \iff n \times 0,8 = 12 \\ & \iff n = \dfrac{12}{0,8} \\ & \iff n = 15 \end{array}$$ Le concurrent doit prévoir15 flèches, pour atteindre en moyenne la cible douze fois.



Partie B


Entre deux phases du concours, pour se perfectionner, le concurrent travaille sa précision latérale sur une autre cible d'entraînement, représentée ci-contre. Pour cela, il tire des flèches pour essayer d'atteindre une bande verticale, de largeur $20$ cm (en grisé sur la figure), le plus près possible de la ligne verticale centrale. On munit le plan contenant la bande verticale d'un repère : la ligne centrale visée est l'axe des ordonnées. On note $X$ la variable aléatoire qui, à toute flèche tirée atteignant ce plan, associe l'abscisse de son point d'impact.

Ainsi, par exemple :
• si la flèche atteint le point A, le tireur a raté la bande, et $X$ prend la valeur $15$ ;
• si elle atteint le point B, l'impact est à la limite de la bande, et $X$ prend la valeur $10$ ;
• si elle atteint le point C, l'impact est dans la bande et $X$ prend la valeur $- 5$.

On suppose que la variable aléatoire $X$ suit une loi normale d'espérance $0$ et d'écart-type $10$.

1. Lorsque la flèche atteint le plan, déterminer la probabilité que son point d'impact soit situé hors de la bande grisée.
On calcule dans un premier temps, la probabilité que le point d’impact soit situé dans la zone grisée.
$p = P(-10 \le X \le 10) \approx 0,693$

La probabilité que le point d’impact soit situé hors de la bande grisée est donc $1 – p \approx 0,317$.
2. Comment modifier les bords de la bande grisée pour faire en sorte que, lorsque la flèche atteint le plan, son point d'impact soit situé à l'intérieur de la bande avec une probabilité égale à $0,6$ ?
On appelle $Z = \dfrac{X}{10}$ . Cette variable aléatoire suit la loi normale centrée réduite.
On cherche la valeur de $a$ telle que :
$$\begin{array}{rl} P(-a \le X \le a) = 0,6 & \iff P\left(-\dfrac{a}{10} \le X \le \dfrac{a}{10}\right) = 0,6 \\ & \iff 2P\left(Z \le \dfrac{a}{10} \right) – 1 = 0,6 \\ & \iff 2P\left(Z \le \dfrac{a}{10} \right) = 1,6 \\ & \iff P\left(Z \le \dfrac{a}{10} \right) = 0,8 \\ & \iff \dfrac{a}{10} \approx 0,8416 \\ & \iff a \approx 8,416
\end{array}$$
Les bords de la cible doivent être situés à $8,416$ cm de l’axe des ordonnées.



Partie C


La durée de vie (exprimée en heures) du panneau électrique affichant le score des concurrents est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 10^{-4}$ (exprimé en h$^{-1}$).

1. Quelle est la probabilité que le panneau fonctionne au moins pendant 2000 heures ?
On veut calculer
$$\begin{array}{rl} P(T \ge 2~000) &= \text{e}^{-\lambda \times 2~000} \\ & = \text{e}^{-0,2} \\ & \approx 0,819 \end{array}$$
La probabilité que le panneau fonctionne au moins pendant 2000 heures est $P(T \ge 2~000)\approx 0,819$


2. Restitution organisée des connaissances
   Dans cette question, $\lambda$ désigne un réel strictement positif. On rappelle que l'espérance mathématique de la variable aléatoire $T$ suivant une loi exponentielle de paramètre $\lambda$, est définie par : E$(T) = \displaystyle\lim_{x \to + \infty} \int_0^x\lambda t \text{e}^{- \lambda t}\text{d}t$.
   1. On considère la fonction $F$, définie pour tout réel $t$ par : $F(t) = \left(- t - \dfrac{1}{\lambda}\right)\text{e}^{- \lambda t}$. Démontrer que la fonction $F$ est une primitive sur $\mathbb R$ de la fonction 1 définie pour tout réel $t$ par : $f(t) = \lambda t\text{e}^{- \lambda t}$.
   $F$ est une fonction dérivable sur $\mathbb R$ en tant que produit de fonctions dérivables sur $\mathbb R$.
   $$\begin{array}{rl} F'(t) &= -\text{e}^{-\lambda t} -\lambda \left(-t – \dfrac{1}{\lambda}\right) \text{e}^{-\lambda t} \\ & = -\text{e}^{-\lambda t} +\lambda t \text{e}^{-\lambda t} + \text{e}^{-\lambda t} \\ &= \lambda t \text{e}^{-\lambda t} \\ &= f(t) \end{array}$$
   La fonction $F$ est donc une primitive sur $\mathbb R$ de $f$.
   
   2. En déduire que l'espérance mathématique de la variable aléatoire $T$ est égale à $\dfrac{1}{\lambda}$. Quelle est l'espérance de durée de vie du panneau électrique affichant le score des concurrents ?
   Soit $x$ un réel positif,
   $$\begin{array} {rl} \displaystyle \int_0^x f(t)\mathrm{d}t & = F(x) – F(0)\\ &= \left(-x – \dfrac{1}{\lambda}\right)\text{e}^{-\lambda x} – \left(-\dfrac{1}{\lambda}\right) \\ & = \dfrac{1}{\lambda} -x\text{e}^{-\lambda x} – \dfrac{1}{\lambda} \text{e}^{-\lambda x} \\ & = \dfrac{1}{\lambda} -\dfrac{\lambda x}{\lambda}\text{e}^{-\lambda x} – \dfrac{1}{\lambda} \text{e}^{-\lambda x} \end{array}$$
   Or $\lim\limits_{x\to +\infty} -\lambda x = -\infty$ et $\lim\limits_{x \to -\infty} x\text{e}^{x} = 0$.
   Par conséquent $\lim\limits_{x \to +\infty} \dfrac{\lambda x}{\lambda}\text{e}^{-\lambda x} = 0$.
   De plus $\lim\limits_{x \to -\infty} \text{e}^x = 0$ donc $\lim\limits_{x \to +\infty} \text{e}^{-\lambda x} = 0$.
   Par conséquent :
   $$\begin{array}{rl} E(T) & = \lim\limits_{x \to +\infty} \int_0^x f(t)\mathrm{d}t \\ & = \lim\limits_{x \to +\infty} \dfrac{1}{\lambda} -\dfrac{\lambda x}{\lambda}\text{e}^{-\lambda x} – \dfrac{1}{\lambda} \text{e}^{-\lambda x} \\ & = \dfrac{1}{\lambda}
   \end{array}$$
   $\quad$
   L’espérance de durée de vie du panneau électrique affichant le score des concurrents est donc $\dfrac{1}{10^{-4}} = 10^4$ heures.



Exercice 2 4 points


Commun à tous les candidats


QCMPour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse, et justifier la réponse. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
Dans les questions 1 et 2, on munit l'espace d'un repère orthonormé, et on considère les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ d'équations respectives$ x+ y + z - 5 = 0$ et $7x - 2y + z - 2 = 0$.

1. Affirmation 1 : les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont perpendiculaires.
2. Affirmation 2 : les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ se coupent suivant la droite de représentation paramétrique: \[\left\{\begin{array}{l c l} x&=&\phantom{- 3}t\\ y&=&\phantom{-}2t + 1\\ z&=&- 3t + 4 \end{array}\right., t \in\mathbb R.\]
3. Un joueur de jeux vidéo en ligne adopte toujours la même stratégie. Sur les 312 premières parties jouées, il en gagne 223. On assimile les parties jouées à un échantillon aléatoire de taille $312$ dans l'ensemble des parties. On souhaite estimer la proportion de parties que va gagner le joueur, sur les prochaines parties qu'il jouera, tout en conservant la même stratégie.
   Affirmation 3 : au niveau de confiance de 95 %, la proportion de parties gagnées doit appartenir à l'intervalle [0,658 ; 0,771].
4. On considère l'algorithme suivant : $$\begin{array}{|c|l|}\hline & a, b \text{ sont deux nombres réels tels que } a < b\\ VARIABLES & x \text{ est un nombre réel }\\ &f \text{ est une fonction définie sur l'intervalle } [a~;~b]\\ \hline &\text{ Lire } a \text{ et } b\\ &\text{ Tant que } b-a > 0,3\\ &\hspace{1cm}x \text{ prend la valeur } \dfrac{a+ b}{2}\\ TRAITEMENT &\hspace{1cm} \text{ Si } f(x) f(a) > 0, \text{ alors } a \text{ prend la valeur } x\\ &\hspace{3.4cm}\text{ sinon } b \text{ prend la valeur } x\\ &\hspace{1cm}\text{ Fin Si }\\ &\text{ Fin Tant que }\\ &\text{ Afficher }\dfrac{a+ b}{2} \\ \hline \end{array}$$ Affirmation 4 : si l'on entre $a = 1, b = 2$ et $f(x) = x^2 - 3$, alors l'algorithme affiche en sortie le nombre 1,6875 .



Correction de l'exercice 2 (4 points)


Commun à tous les candidats

QCMPour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse, et justifier la réponse. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
Dans les questions 1 et 2, on munit l'espace d'un repère orthonormé, et on considère les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ d'équations respectives$ x+ y + z - 5 = 0$ et $7x - 2y + z - 2 = 0$.

1. Affirmation 1 : les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont perpendiculaires.
Affirmation 1 : Fausse
On appelle $\vec{n}_1(1;1;1)$ et $\vec{n_2}(7;-2;1)$ des vecteurs normaux respectivement aux plans $\mathscr{P}_1$ et $\mathscr{P}_2$.
$\vec{n}_1.\vec{n}_2 = 7 -2 + 1 = 6 \neq 0$.

Ces deux vecteurs ne sont pas orthogonaux. Par conséquent les plans ne sont pas perpendiculaires.

Affirmation 1 : fausse

2. Affirmation 2 : les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ se coupent suivant la droite de représentation paramétrique: \[\left\{\begin{array}{l c l} x&=&\phantom{- 3}t\\ y&=&\phantom{-}2t + 1\\ z&=&- 3t + 4 \end{array}\right., t \in\mathbb R.\]
Affirmation 2 : Vraie
Notons $\Delta$, la droite de représentation paramétrique : $\left\{\begin{array}{l c l} x&=&\phantom{- 3}t\\ y&=&\phantom{-}2t + 1\\ z&=&- 3t + 4 \end{array}\right., t \in\mathbb R.$

Les deux vecteurs n’étant clairement pas colinéaires, les plans sont sécants.
regardons si la droite dont une représentation paramétrique nous est fournie est incluse dans chacun des plans.
Pour le plan $\mathscr{P}_1$ :
$ t + 2t + 1 -3t + 4 – 5 = 3t – 3t + 5 – 5 = 0$, ainsi $\Delta\subset \mathscr{P}_1$
Pour le plan $\mathscr{P}_2$ :
$7t – 2(2t + 1) + (-3t + 4) – 2 = 7t – 4t -2 -3t + 4 – 2 = 0$, ainsi $\Delta\subset \mathscr{P}_2$.
$\quad$
La représentation paramétrique fournie vérifie bien les équations cartésiennes des deux plans. Il s’agit donc bien de la représentation paramétrique de la l’intersection des plans $\mathscr{P}_1$ et $\mathscr{P}_2$.

Affirmation 2 : vraie

3. Un joueur de jeux vidéo en ligne adopte toujours la même stratégie. Sur les 312 premières parties jouées, il en gagne 223. On assimile les parties jouées à un échantillon aléatoire de taille $312$ dans l'ensemble des parties. On souhaite estimer la proportion de parties que va gagner le joueur, sur les prochaines parties qu'il jouera, tout en conservant la même stratégie.
   Affirmation 3 : au niveau de confiance de 95 %, la proportion de parties gagnées doit appartenir à l'intervalle [0,658 ; 0,771].

La fréquence est égale à  $\1$. La taille $n$ de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times \8  =\3$  et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times \8 \geq 5 \text{ et } n\times (1-\8) \geq 5$$

L' intervalle de confiance avec un niveau de confiance de 95% est : \[I = \left[f - \dfrac{1}{\sqrt{n}}~;~f +\dfrac{1}{\sqrt{n}} \right]\]
La fréquence est $\8=\1$.

• On arrondit la borne inférieure par défaut à $10^{-\7}$ près : $\1 - \dfrac{1}{\sqrt{\2}}\approx \10$ soit $\5$.
• On arrondit la borne supérieure par excés à $10^{-\7}$ près : $\1 + \dfrac{1}{\sqrt{\2}}\approx \11$ soit $\6$.


L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - \dfrac{1}{\sqrt{\2}}~;~\1 + \dfrac{1}{\sqrt{\2}} \right]\approx[\5~;~\6]\] 



Affirmation 3 : vraie

4. On considère l'algorithme suivant : $$\begin{array}{|c|l|}\hline & a, b \text{ sont deux nombres réels tels que } a < b\\ VARIABLES & x \text{ est un nombre réel }\\ &f \text{ est une fonction définie sur l'intervalle } [a~;~b]\\ \hline &\text{ Lire } a \text{ et } b\\ &\text{ Tant que } b-a > 0,3\\ &\hspace{1cm}x \text{ prend la valeur } \dfrac{a+ b}{2}\\ TRAITEMENT &\hspace{1cm} \text{ Si } f(x) f(a) > 0, \text{ alors } a \text{ prend la valeur } x\\ &\hspace{3.4cm}\text{ sinon } b \text{ prend la valeur } x\\ &\hspace{1cm}\text{ Fin Si }\\ &\text{ Fin Tant que }\\ &\text{ Afficher }\dfrac{a+ b}{2} \\ \hline \end{array}$$ Affirmation 4 : si l'on entre $a = 1, b = 2$ et $f(x) = x^2 - 3$, alors l'algorithme affiche en sortie le nombre 1,6875 .
Affirmation 4 :Fausse
Effectuons les premières étapes
$a = 1$ et $b = 2$ donc $b-a = 1 > 0,3$
$x = 1,5$ or $f(1,5) = -0,75$ et $f(1) = -2$ donc $f(x)f(a) > 0$
$\quad$
Par conséquent $a = 1,5$ et $b= 2$ et $b-a= 0,5 > 0,3$
$x= 1,75$ or $f(1,75) = 0,0625$ et $f(1,5) = -0,75$ donc $f(x)f(a) <0$
$\quad$Par conséquent $a=1,5$ et $b=1,75$. Mais $1,75 – 1,5 = 0,25 <3$.
L’algorithme affiche donc $\dfrac{1,5 + 1,75}{2} = 1,625$.

Affirmation 4 : fausse



Exercice 3 6 points


Fonctions


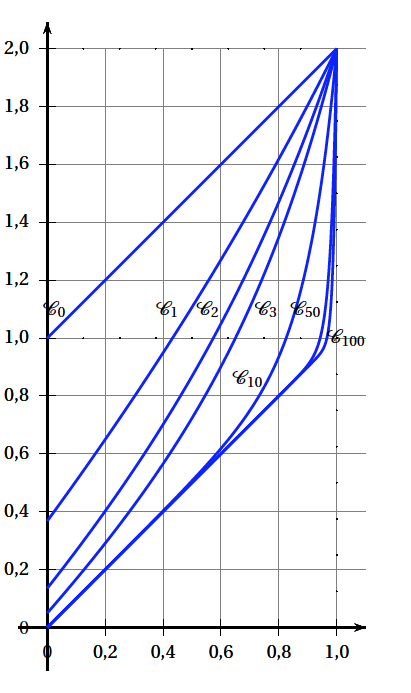
Pour tout entier naturel $n$, on définit la fonction $f_n$ pour tout réel $x$ de l'intervalle [0 ; 1] par : \[f_n(x) = x + \text{e}^{n (x - 1)}.\] On note $\mathcal{C}_n$ la représentation graphique de la fonction $f_n$ dans un repère orthogonal. Quelques-unes des courbes $\mathcal{C}_n$ sont représentées ci-dessous.


Partie A : généralités sur les fonctions $f_n$



1. Démontrer que, pour tout entier naturel $n$, la fonction $f_n$ est croissante et positive sur l'intervalle [0 ; 1].
2. Montrer que les courbes $\mathcal{C}_n$ ont toutes un point commun A, et préciser ses coordonnées.
3. À l'aide des représentations graphiques, peut-on conjecturer le comportement des coefficients directeurs des tangentes en A aux courbes $\mathcal{C}_n$ pour les grandes valeurs de $n$ ? Démontrer cette conjecture.



Partie B : évolution de $f_n(x)$ lorsque $x$ est fixé


Soit $x$ un réel fixé de l'intervalle [0 ; 1] . Pour tout entier naturel $n$, on pose $u_n = f_n (x)$.

1. Dans cette question, on suppose que $x = 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.
2. Dans cette question, on suppose que $0 \leqslant x < 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.



Partie C : aire sous les courbes $\mathcal{C}_n$


Pour tout entier naturel $n$, on note $A_n$ l'aire, exprimée en unité d'aire, du domaine situé entre l'axe des abscisses, la courbe $\mathcal{C}_n$ et les droites d'équations respectives $x = 0$ et $x = 1$. À partir des représentations graphiques, conjecturer la limite de la suite $\left(A_n\right)$ lorsque l'entier $n$ tend vers $+ \infty$, puis démontrer cette conjecture.


Correction de l'exercice 3 (5 points)


Commun à tous les candidats


Fonctions


Pour tout entier naturel $n$, on définit la fonction $f_n$ pour tout réel $x$ de l'intervalle [0 ; 1] par : \[f_n(x) = x + \text{e}^{n (x - 1)}.\] On note $\mathcal{C}_n$ la représentation graphique de la fonction $f_n$ dans un repère orthogonal. Quelques-unes des courbes $\mathcal{C}_n$ sont représentées ci-dessous.


Partie A : généralités sur les fonctions $f_n$



1. Démontrer que, pour tout entier naturel $n$, la fonction $f_n$ est croissante et positive sur l'intervalle [0 ; 1].
Pour tout entier naturel $n$, la fonction $f_n$ est croissante sur $[0;1]$ en tant que somme de fonctions croissantes sur cet intervalle.
On peut aussi remarquer que la fonction $f_n$ estdérivables sur $[0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
$f_n'(x)=1+n\text{e}^{n (x - 1)}$

• Premier cas $n=0$
  $f_0(x)=x+ \text{e}^{0 (x - 1)}=x$
  $f_0'(x)=1> 0 $; ainsi $f_0$ est croissante et positive sur l'intervalle [0 ; 1].
• Deuxième cas : $n\geq 1$
  $f_n(x)=x+ \text{e}^{ n(x - 1)}=x$
  $f_n'(x)=1+ n\text{e}^{ (x - 1)}> 0 $; ainsi $f_n$ est croissante sur l'intervalle [0 ; 1].
$\quad$
De plus, sur $[0;1]$, $x \ge 0$ et la fonction exponentielle étant strictement positive sur $\mathbb R$, on a $\text{e}^{n(x-1)} > 0$.
Par conséquent, pour tout $x \in [0;1]$, $f_n(x) \ge 0$.

2. Montrer que les courbes $\mathcal{C}_n$ ont toutes un point commun A, et préciser ses coordonnées.
Montrons que le point $A(1;2)$ appartient à toutes les courbes $C_n$.
Pour tout entier naturel $n$, on a $f_n(1) = 1 + \text{e}^0 = 2$.
Le point $A(1;2)$ appartient bien à toutes les courbes $C_n$.

3. À l'aide des représentations graphiques, peut-on conjecturer le comportement des coefficients directeurs des tangentes en A aux courbes $\mathcal{C}_n$ pour les grandes valeurs de $n$ ? Démontrer cette conjecture.
Il semblerait que les coefficients directeurs des tangentes en A aux courbes $C_n$ soient les termes d’une suite croissante de limite $+\infty$.
$\quad$.
Pour tout entier naturel $n$, la fonction $f_n$ est dérivable sur $[0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
$ f_n'(x) = 1 +n\text{e}^{n(x-1)}$.
Or le coefficient directeur de la tangente en A à la courbe $C_n$ est donné par $f_n'(1) = 1 + n$.
La suite $(1+n)_{n\in \mathbb N}$ est clairement croissante et de limite $+\infty$.



Partie B : évolution de $f_n(x)$ lorsque $x$ est fixé


Soit $x$ un réel fixé de l'intervalle [0 ; 1] . Pour tout entier naturel $n$, on pose $u_n = f_n (x)$.

1. Dans cette question, on suppose que $x = 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.
Si $x=1$, on a alors $u_n = 1 + 1 = 2$.
La suite $(u_n)$ est donc constante et a pour limite $2$.

2. Dans cette question, on suppose que $0 \leqslant x < 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.
Si $0 \le x <1$ on a alors $u_n = x + \left(e^{x-1}\right)^n$.
Or $x-1 < 0 $ donc $0 < \text{e}^{x-1} < 1$ et $\lim\limits_{n \to +\infty} \left(e^{x-1}\right)^n = 0$.
Par conséquent $\lim\limits_{n \to +\infty} u_n = x$.



Partie C : aire sous les courbes $\mathcal{C}_n$



Pour tout entier naturel $n$, on note $A_n$ l'aire, exprimée en unité d'aire, du domaine situé entre l'axe des abscisses, la courbe $\mathcal{C}_n$ et les droites d'équations respectives $x = 0$ et $x = 1$. À partir des représentations graphiques, conjecturer la limite de la suite $\left(A_n\right)$ lorsque l'entier $n$ tend vers $+ \infty$, puis démontrer cette conjecture.

Le domaine délimité par la courbe $f_n$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$ semble se rapprocher de plus en plus d’un triangle rectangle isocèle de côté $1$. Par conséquent la limite de $A_n$ semble être $\dfrac{1}{2}$.

On a pour $n\geq 1$:

$$\begin{array}{rl} A_n & = \displaystyle \int_0^1 f_n(x) \mathrm{d}x\\ & = \left[\dfrac{x^2}{2} + \dfrac{1}{n}\text{e}^{n(x-1)}\right]_0^1\\ & = \dfrac{1}{2} + \dfrac{1}{n}\left(1 – \text{e}^{-n}\right) \end{array}$$
Or $\lim\limits_{n \to +\infty} e^{-n} = 0$ et $\lim\limits_{n \to +\infty} \dfrac{1}{n} = 0$.
Par conséquent, par somme et produit des limites $\lim\limits_{n \to +\infty} A_n = \dfrac{1}{2}$.

Une animation sous Geogebra


 




Exercice 4 5 points


Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques


Le plan est muni du repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On donne le nombre complexe $\text{j} = - \dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$. Le but de cet exercice est d'étudier quelques propriétés du nombre j et de mettre en évidence un lien de ce nombre avec les triangles équilatéraux.


Partie A : propriétés du nombre $j$



1. 1. Résoudre dans l'ensemble $\mathbb C$ des nombres complexes l'équation \[z^2 + z + 1 = 0.\]
   2. Vérifier que le nombre complexe j est une solution de cette équation.
2. Déterminer le module et un argument du nombre complexe j, puis donner sa forme exponentielle.
3. Démontrer les égalités suivantes:
   1. $\text{j} ^3 = 1$ ;
   2. $\text{j} ^2 = - 1 - \text{j}$.
4. On note P, Q, R les images respectives des nombres complexes 1,j et j$^2$ dans le plan. Quelle est la nature du triangle PQR ? Justifier la réponse.



Partie B


Soit $a$, $b$, $c$ trois nombres complexes vérifiant l'égalité $a+ \text{j}b + \text{j}^2 c = 0$. On note A, B, C les images respectives des nombres $a$, $b$, $c$ dans le plan.

1. En utilisant la question A - 3. b., démontrer l'égalité : $ a - c = \text{j}(c - b)$.
2. En déduire que AC = BC .
3. Démontrer l'égalité : $a - b = \text{j}^2 (b - c)$.
4. En déduire que le triangle ABC est équilatéral.



Correction de l'exercice 4 5 points


Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques


Le plan est muni du repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On donne le nombre complexe $\text{j} = - \dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$. Le but de cet exercice est d'étudier quelques propriétés du nombre j et de mettre en évidence un lien de ce nombre avec les triangles équilatéraux.


Partie A : propriétés du nombre $j$



1. 1. Résoudre dans l'ensemble $\mathbb C$ des nombres complexes l'équation \[z^2 + z + 1 = 0.\]
   $\Delta = 1^2 – 4 = -3<0$
   Cette équation possède donc deux racines complexes conjuguées :
   $$z_1 = \dfrac{-1 – \text{i} \sqrt{3}}{2} \quad \text{ et } \quad z_2 = \dfrac{-1 + \text{i}\sqrt{3}}{2}$$
   
   2. Vérifier que le nombre complexe j est une solution de cette équation.
   $z_2 = \dfrac{-1 + \text{i}\sqrt{3}}{2} = -\dfrac{1}{2} + \text{i} \dfrac{\sqrt{3}}{2} = j$.
   Donc $j$ est une solution de cette équation.
2. Déterminer le module et un argument du nombre complexe j, puis donner sa forme exponentielle.
$|j| =\sqrt{a^2+b^2}= \sqrt{\dfrac{1}{4} + \dfrac{3}{4}} = 1$.
$\begin{cases}\cos(\theta) = \dfrac{a}{r}= - \dfrac{1}{2}\\ \sin(\theta) = \dfrac{b}{r}= \dfrac{\sqrt{3}}{2}\\ \end{cases}$ on déduit donc arg$(j)= \dfrac{2\pi}{3}$.
Donc $j = \text{e}^{2\pi\text{i} /3}$

3. Démontrer les égalités suivantes:
   1. $\text{j} ^3 = 1$ ;
   $j^3 = \left(\text{e}^{2\text{i} \pi /3}\right)^3 = \text{e}^{\text{i}2 \pi} =\text{e}^{\text{i}\times 0}= 1$
   
   2. $\text{j} ^2 = - 1 - \text{j}$.
   $j$ est solution de l’équation $z^2 + z +1 = 0$.
   $\quad$
   Par conséquent $j^2 + j + 1 = 0 \iff j^2 = -1 – j$.
4. On note P, Q, R les images respectives des nombres complexes 1,j et j$^2$ dans le plan. Quelle est la nature du triangle PQR ? Justifier la réponse.
On a ainsi $PQ = |1 – j| = \sqrt{\left(\dfrac{3}{2}\right)^2 + \dfrac{3}{4}} = \sqrt{3}$.
$PR = \left|1 – j^2\right| = |2 + j| = \sqrt{\left(\dfrac{3}{2}\right)^2 + \dfrac{3}{4}} = \sqrt{3}$.
$QR = |-1 – j – j| = |-1 – 2j|= \left|-1 + 1 + \sqrt{3}\text{i}\right| = \sqrt{3}$.
Le triangle $PQR$ est donc équilatéral.



Partie B


Soit $a$, $b$, $c$ trois nombres complexes vérifiant l'égalité $a+ \text{j}b + \text{j}^2 c = 0$. On note A, B, C les images respectives des nombres $a$, $b$, $c$ dans le plan.

1. En utilisant la question A - 3. b., démontrer l'égalité : $ a - c = \text{j}(c - b)$.
$$\begin{array}{rl} a + jb + j^2c = 0 & \iff a + jb + (-1-j)c = 0\\ & \iff a + jb – c – jc = 0\\ & \iff a – c = j(c – b) \end{array}$$

2. En déduire que AC = BC .
On a :
$$\begin{array}{rl} AC &= |c- a| \\ &= |a – c| \\ &= |j| |c – b| \\ &= |c – b| \\ &= BC \end{array}$$

3. Démontrer l'égalité : $a - b = \text{j}^2 (b - c)$.
$$\begin{array}{rl} a – b & = -jb – j^2 c – b\\ & = (-1 – j)b – j^2 c\\ &= j^2b – j^2 c\\ &= j^2 (b – c) \end{array}$$

4. En déduire que le triangle ABC est équilatéral.
On a $j^2 = \left(\text{e}^{2\pi\text{i} /3}\right)^2 = \text{e}^{4\pi\text{i} /3}$.
Par conséquent $\left|j^2\right| = 1$.
Donc :
$$\begin{array}{rl} BA & = |a – b| \\ & = \left|j^2\right||b – c| \\ & = |b – c| \\ & = CB \end{array}$$
Ainsi $AC = BC = AB$.
Le triangle $ABC$ est donc équilatéral.



Spécialité 5 points


Candidats AYANT SUIVI l'enseignement de spécialité mathématiques


On dit qu'un entier naturel non nul $N$ est un nombre triangulaire s'il existe un entier naturel $n$ tel que : $N = 1+2+ \ldots + n$. Par exemple, 10 est un nombre triangulaire car $10 = 1 + 2 + 3 + 4$. Le but de ce problème est de déterminer des nombres triangulaires qui sont les carrés d'un entier.
On rappelle que, pour tout entier naturel non nul $n$, on a : \[ 1 + 2 + \ldots + n = \dfrac{n(n + 1)}{2}.\]

Partie A : nombres triangulaires et carrés d'entiers



1. Montrer que $36$ est un nombre triangulaire, et qu'il est aussi le carré d'un entier.
2. 1. Montrer que le nombre $1 + 2 + \ldots + n$ est le carré d'un entier si et seulement s'il existe un entier naturel $p$ tel que : $n^2 + n - 2 p^2 = 0$.
   2. En déduire que le nombre $1 + 2 + \ldots + n$ est le carré d'un entier si et seulement s'il existe un entier naturel $p$ tel que : $(2n + 1)^2 - 8 p^2 = 1$.



Partie B : étude de l'équation diophantienne associée


On considère (E) l'équation diophantienne \[x^2 - 8 y^2 = 1,\] où $x$ et $y$ désignent deux entiers relatifs.

1. Donner deux couples d'entiers naturels inférieurs à 10 qui sont solution de (E).
2. Démontrer que, si un couple d'entiers relatifs non nuls $(x~;~y)$ est solution de (E), alors les entiers relatifs $x$ et $y$ sont premiers entre eux.



Partie C : lien avec le calcul matriciel


Soit $x$ et $y$ deux entiers relatifs. On considère la matrice $A = \begin{pmatrix}3&8\\1&3\end{pmatrix}$. On définit les entiers relatifs $x'$ et $y'$ par l'égalité : $\begin{pmatrix}x'\\y'\end{pmatrix} = A\begin{pmatrix}x\\y\end{pmatrix}$.

1. Exprimer $x'$ et $y'$ en fonction de $x$ et de $y$.
2. Déterminer la matrice $A^{-1}$, puis exprimer $x$ et $y$ en fonction de $x'$ et $y'$.
3. Démontrer que $(x~;~y)$ est solution de (E) si et seulement si $(x'~;~y')$ est solution de (E).
4. On considère les suites $\left(x_n\right)$ et $\left(y_n\right)$ définies par $x_0 = 3$, $y_0 = 1$ et, pour tout entier naturel $n$, $\begin{pmatrix}x_{n+1}\\y_{n+1}\end{pmatrix} = A\begin{pmatrix}x_n\\y_n\end{pmatrix}$. On admet que, ainsi définis, les nombres $x_n$ et $y_n$ sont des entiers naturels pour toute valeur de l'entier $n$. Démontrer par récurrence que, pour tout entier naturel $n$, le couple $\left(x_n~;~y_n\right)$ est solution de (E).



Partie D : retour au problème initial


À l'aide des parties précédentes, déterminer un nombre triangulaire supérieur à 2015 qui est le carré d'un entier.


Correction de l'exercice de Spécialité 5 points


Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

On dit qu'un entier naturel non nul $N$ est un nombre triangulaire s'il existe un entier naturel $n$ tel que : $N = 1+2+ \ldots + n$. Par exemple, 10 est un nombre triangulaire car $10 = 1 + 2 + 3 + 4$. Le but de ce problème est de déterminer des nombres triangulaires qui sont les carrés d'un entier.
On rappelle que, pour tout entier naturel non nul $n$, on a : \[ 1 + 2 + \ldots + n = \dfrac{n(n + 1)}{2}.\]

Partie A : nombres triangulaires et carrés d'entiers

1. Montrer que $36$ est un nombre triangulaire, et qu'il est aussi le carré d'un entier.
$36 = 1 + 2 + 3 + 4 + 5 +6 + 7 + 8$
Donc $36$ est un nombre triangulaire.
De plus $36 = 6^2$ c’est également le carré d’un entier.
$36$ est un nombre triangulaire, et est aussi le carré d'un entier.


2. 1. Montrer que le nombre $1 + 2 + \ldots + n$ est le carré d'un entier si et seulement s'il existe un entier naturel $p$ tel que : $n^2 + n - 2 p^2 = 0$.
   $1 + 2 + \ldots + n = \dfrac{n(n+1)}{2}$.
   Par conséquent $1 + 2 + \ldots + n$ est le carré d’un entier si, et seulement s’il existe un entier naturel $p$ tel que :
   $\dfrac{n(n+1)}{2} = p^2 \iff n(n+1) = 2p^2 \iff n^2 + n – 2p^2 = 0$.
   
   2. En déduire que le nombre $1 + 2 + \ldots + n$ est le carré d'un entier si et seulement s'il existe un entier naturel $p$ tel que : $(2n + 1)^2 - 8 p^2 = 1$.
   $$\begin{array}{rl} n^2+n-2p^2 = 0 & \iff 4\left(n^2 + n – 2p^2\right) = 0\\ & \iff 4n^2 + 4n – 8p^2 = 0\\ & \iff 4n^2 + 4n + 1 – 1 – 8p^2 = 0\\ & \iff (2n + 1)^2 – 1 – 8p^2 = 0\\ & \iff (2n+1)^2 – 8p^2 = 1 \end{array}$$
   
   Donc le nombre $1 + 2 +\ldots + n$ est le carré d’un entier si, et seulement s’il existe un entier naturel $p$ tel que $(2n+1)^2 – 8p^2 = 1$.
   
   
   

Partie B : étude de l'équation diophantienne associée

On considère (E) l'équation diophantienne \[x^2 - 8 y^2 = 1,\] où $x$ et $y$ désignent deux entiers relatifs.

1. Donner deux couples d'entiers naturels inférieurs à 10 qui sont solution de (E).
$3^2 – 8\times 1^2 = 9 – 8 = 1$. Le couple $(3;1)$ est donc solution de $(E)$.
$1^2 – 8 \times 0^2 = 1$. Le couple $(1;0)$ est donc solution de $(E)$.

2. Démontrer que, si un couple d'entiers relatifs non nuls $(x~;~y)$ est solution de (E), alors les entiers relatifs $x$ et $y$ sont premiers entre eux.
Soit $(x;y)$ un couple de solution de $(E)$ alors
$x^2 – 8y^2 = 1$.
D’après le théorème de Bezout, les nombres $x^2$ et $y^2$ sont donc premiers entre eux.
Supposons que $a$ soit un diviseur commun à $x$ et $y$.
Alors $a$ divise également $x\times x = x^2$ et $y \times y = y^2$.
Or ces deux nombres sont premiers entre eux.
Par conséquent $x$ et $y$ le sont également.

Partie C : lien avec le calcul matriciel

Soit $x$ et $y$ deux entiers relatifs. On considère la matrice $A = \begin{pmatrix}3&8\\1&3\end{pmatrix}$. On définit les entiers relatifs $x'$ et $y'$ par l'égalité : $\begin{pmatrix}x'\\y'\end{pmatrix} = A\begin{pmatrix}x\\y\end{pmatrix}$.

1. Exprimer $x'$ et $y'$ en fonction de $x$ et de $y$.
$\quad$
$\begin{pmatrix} x’ \\y’ \end{pmatrix} = A \begin{pmatrix} x \\y \end{pmatrix} = \begin{pmatrix} 3x + 8y \\x+ 3y \end{pmatrix}$
Donc $x’= 3x + 8y$ et $y’ = x + 3y$.

2. Déterminer la matrice $A^{-1}$, puis exprimer $x$ et $y$ en fonction de $x'$ et $y'$.
$A^{-1} = \dfrac{1}{9 – 8} \begin{pmatrix} 3 &-8 \\-1& 3\end{pmatrix} = \begin{pmatrix} 3 &-8 \\-1& 3\end{pmatrix}$.
$\quad$
On a ainsi $\begin{pmatrix} x \\y \end{pmatrix} = A^{-1} \begin{pmatrix} x’ \\y’ \end{pmatrix} = \begin{pmatrix} 3x’ – 8y’ \\-x’+ 3y’ \end{pmatrix}$
Donc $x= 3x’ – 8y’$ et $y = -x’ + 3y$.
3. Démontrer que $(x~;~y)$ est solution de (E) si et seulement si $(x'~;~y')$ est solution de (E).
Supposons que $(x;y)$ soit solution de $(E)$ alors :
$$\begin{array}{rl} x’^2 – 8y’^2 &= (3x+8y)^2 – 8(x+3y)^2\\ &= 9x^2 +48xy + 64y^2 – 8x^2 -48xy -72y^2\\ &= x^2 – 8y^2\\ & = 1
\end{array}$$
Ainsi $(x';y’)$ est également solution de $(E)$.
$\quad$
Réciproquement, supposons que $(x';y’)$ soit solution de $(E)$ alors :
$$\begin{array}{rl} x^2-8y^2 & = (3x’-8y’)^2 – 8(-x’+3y’)^2\\ & = 9x’^2 – 48x’y’ + 64y’^2 – 8x’^2 + 48x’y’ – 72y’^2\\ &= x’^2 – 8y’^2\\ &= 1
\end{array}$$
Ainsi $(x;y)$ est également solution de $(E)$.

4. On considère les suites $\left(x_n\right)$ et $\left(y_n\right)$ définies par $x_0 = 3$, $y_0 = 1$ et, pour tout entier naturel $n$, $\begin{pmatrix}x_{n+1}\\y_{n+1}\end{pmatrix} = A\begin{pmatrix}x_n\\y_n\end{pmatrix}$. On admet que, ainsi définis, les nombres $x_n$ et $y_n$ sont des entiers naturels pour toute valeur de l'entier $n$. Démontrer par récurrence que, pour tout entier naturel $n$, le couple $\left(x_n~;~y_n\right)$ est solution de (E).
Initialisation :
si $n=0$ alors $x_0=3$ et $y_0 = 1$
D’après la question B.1 le couple $(3;1)$ est solution de l’équation $(E)$.
Ainsi la propriété est vraie au rang $0$.
$\quad$
Hérédité :
Supposons la propriété vraie au rang $n$: $(x_n;y_n)$ est solution de $(E)$.
Alors d’après la question C.3 le couple $(x';y’)$ défini par $\begin{pmatrix} x’ \\y’ \end{pmatrix} = A \begin{pmatrix} x \\y \end{pmatrix}$ est également solution de $(E)$.
Donc $(x_{n+1};y_{n+1})$ est solution de $(E)$.
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion :
La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, le couple $(x_n;y_n)$ est solution de $(E)$.

Partie D : retour au problème initial

$N = 1 + 2 + \ldots + n$ est un nombre triangulaire supérieur à $2~015$ et également le carré d’un entier alors il vérifie $N \ge 2~015$ et $(2n +1)^2 – 8p^2 = 1$.
Si on prend $n \geq 2~015$ alors la condition $N \ge  2015$ est évidemment vérifiée.
Par conséquent $2n+1 \ge 4031$.
On utilise la suite de couple $(x_n;y_n)$ définie dans la partie précédente. On cherche un couple tel que $x_n \geq 4031$.

On obtient les couples suivants :

$(17;6)$
$(99;35)$
$(577;204)$
$(3~363;1~189)$
$(19~601;6~930)$

Ainsi $2n + 1 = 19~601$ soit $n= 9~800$.

On a alors $N = \dfrac{n(n+1)}{2} = 48~0824~900$ est un nombre triangulaire. De plus $N$ est le carré de $6~930$.
Ce n’est, cependant, pas le plus petit nombre cherché.