Baccalauréat S Amérique du Sud 24 novembre 2015

 

 

Exercice 1 5 points

Commun à tous les candidats

Partie A

Dans le plan muni d'un repère orthonormé $(,O;\vec{i},\vec{j} \,)$ on désigne par $\mathcal{C}_u$ la courbe représentative de la fonction $u$ définie sur l'intervalle $]0;+ \infty[$ par : $$u(x) = a + \dfrac{b}{x} + \dfrac{c}{x^2}$$ où $a, b$ et $c$ sont des réels fixés. On a tracé sur le graphique ci-dessous la courbe $\mathcal{C}_u$ et la droite $\mathcal{D}$ d'équation $y = 1$.

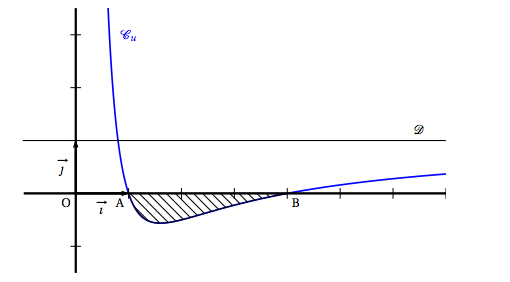
On précise que la courbe $\mathcal{C}_u$ passe par les points A(1;0) et B(4;0) et que l'axe des ordonnées et la droite $\mathcal{D}$ sont asymptotes à la courbe $\mathcal{C}_u$.

1. Donner les valeurs de $u(1)$ et $u(4)$.
2. Donner $\displaystyle\lim_{x \to + \infty} u(x)$. En déduire la valeur de $a$.
3. En déduire que, pour tout réel $x$ strictement positif, $u(x) = \dfrac{x^2 - 5x + 4}{x^2}$.

 

Partie B

Soit $f$ la fonction définie sur l'intervalle $]0;+ \infty[$ par : $$f(x) = x - 5\ln x - \dfrac{4}{x}.$$

1. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $0$. On pourra utiliser sans démonstration le fait que $\displaystyle\lim_{x \to 0} x \ln x = 0$.
2. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $+ \infty$.
3. Démontrer que, pour tout réel $x$ strictement positif, $f'(x) = u(x)$. En déduire le tableau de variation de la fonction $f$ en précisant les limites et les valeurs particulières.

 

Partie C

 

1. Déterminer l'aire $\mathcal{A}$, exprimée en unité d'aire, du domaine hachuré sur le graphique de la \textbf{partie A}.
2. Pour tout réel $\lambda$ supérieur ou égal à 4, on note $\mathcal{A}_{\lambda}$ l'aire, exprimée en unité d'aire, du domaine formé par les points $M$ de coordonnées $(x;y)$ telles que $$4 \leqslant x \leqslant \lambda\quad \text{et}\quad 0 \leqslant y \leqslant u(x).$$ Existe-t-il une valeur de $\lambda$ pour laquelle $\mathcal{A}_{\lambda} = \mathcal{A}$ ? Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise en compte dans l'évaluation.

 

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Partie A

Dans le plan muni d'un repère orthonormé $(,O;\vec{i},\vec{j} \,)$ on désigne par $\mathcal{C}_u$ la courbe représentative de la fonction $u$ définie sur l'intervalle $]0;+ \infty[$ par : $$u(x) = a + \dfrac{b}{x} + \dfrac{c}{x^2}$$ où $a, b$ et $c$ sont des réels fixés. On a tracé sur le graphique ci-dessous la courbe $\mathcal{C}_u$ et la droite $\mathcal{D}$ d'équation $y = 1$.

On précise que la courbe $\mathcal{C}_u$ passe par les points A(1;0) et B(4;0) et que l'axe des ordonnées et la droite $\mathcal{D}$ sont asymptotes à la courbe $\mathcal{C}_u$.

1. Donner les valeurs de $u(1)$ et $u(4)$.
La courbe $\mathscr{C}_u$ passe par $A(1;0)$ par conséquent $u(1)=0$.
Elle passe également pas $B(4;0)$ donc $u(4)=0$.
$\quad$
2. Donner $\displaystyle\lim_{x \to + \infty} u(x)$. En déduire la valeur de $a$.
$\lim\limits_{x\to +\infty} \dfrac{1}{x}=0$ et $\lim\limits_{x\to +\infty} \dfrac{1}{x^2}=0$.
Donc $\lim\limits_{x\to +\infty} u(x)=a$.
La droite d’équation $y=1$ étant asymptote à la courbe $\mathscr{C}_u$ cela signifie donc que $a=1$.
$\quad$
3. En déduire que, pour tout réel $x$ strictement positif, $u(x) = \dfrac{x^2 - 5x + 4}{x^2}$.
Ainsi $u(x)=1+\dfrac{b}{x}+\dfrac{c}{x^2}$.
Puisque $u(1)=0$ on obtient $1+b+c=0$ soit $b+c=-1 \quad (1)$.
Puisque $u(4)=0$ on obtient $1+\dfrac{b}{4}+\dfrac{c}{16}=0$ soit $16+4b+c=0$ ou encore $4b+c=-16 \quad (2)$.
On fait $(2)-(1)$ : $3b=-15$ soit $b=-5$
Ainsi $-5+c=-1$ soit $c=4$.
On vérifie dans l’équation $2$ $4\times (-5)+4=-20+4=-16$
$\quad$
Par conséquent $u(x)=1-\dfrac{5}{x}+\dfrac{4}{x^2} = \dfrac{x^2-5x+4}{x^2}$.
$\quad$

 

Partie B

Soit $f$ la fonction définie sur l'intervalle $]0;+ \infty[$ par : $$f(x) = x - 5\ln x - \dfrac{4}{x}.$$

1. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $0$. On pourra utiliser sans démonstration le fait que $\displaystyle\lim_{x \to 0} x \ln x = 0$.
$f(x)=\dfrac{x^2-5x\ln x-4}{x}$.
$\lim\limits_{x \to 0^+} x\ln x=0$ donc $\lim\limits_{x \to 0^+}x^2-5x\ln x-4 = -4$
Or $\lim\limits_{x \to 0^+} x=0^+$
Par conséquent $\lim\limits_{x \to 0^+} f(x)=-\infty$.
$\quad$
2. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $+ \infty$.
$f(x)=x\left(1-\dfrac{\ln x}{x}-\dfrac{4}{x^2}\right)$.
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0$ et $\lim\limits_{x \to +\infty} \dfrac{1}{x^2}=0$.
Donc $\lim\limits_{x \to +\infty} \left(1-\dfrac{\ln x}{x}-\dfrac{4}{x^2}\right) =1$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$.
$\quad$
3. Démontrer que, pour tout réel $x$ strictement positif, $f'(x) = u(x)$. En déduire le tableau de variation de la fonction $f$ en précisant les limites et les valeurs particulières.
La fonction $f$ est dérivable sur $]0;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
$f'(x)=1-5\times \dfrac{1}{x}+\dfrac{4}{x^2} = u(x)$.
Le signe de $u(x)$ ne dépend que de celui de $x^2-5x+4=(x-1)(x-4)$
On obtient ainsi le tableau de variations suivant :

 

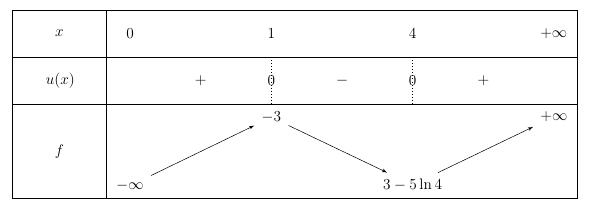
Partie C

 

1. Déterminer l'aire $\mathcal{A}$, exprimée en unité d'aire, du domaine hachuré sur le graphique de la \textbf{partie A}.
L’aire hachurée correspond à l’aire du domaine situé entre l’axe des abscisses, la courbe $\mathscr{C}_u$ et les droites d’équation $x=0$ et $x=4$.
La fonction $-u$ est continue et positive sur $[1;4]$.
Ainsi :
$\begin{align*} \mathscr{A}&=\int_1^4-u(x)\mathrm{d}x\phantom{\dfrac{1}{4}} \\\\ &=-\left(f(4)-f(1)\right) \\\\ &=-(3-5\ln 4 +3) \\\\ &=5\ln 4-6 \end{align*}$
$\quad$
2. Pour tout réel $\lambda$ supérieur ou égal à 4, on note $\mathcal{A}_{\lambda}$ l'aire, exprimée en unité d'aire, du domaine formé par les points $M$ de coordonnées $(x;y)$ telles que $$4 \leqslant x \leqslant \lambda\quad \text{et}\quad 0 \leqslant y \leqslant u(x).$$ Existe-t-il une valeur de $\lambda$ pour laquelle $\mathcal{A}_{\lambda} = \mathcal{A}$ ? Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise en compte dans l'évaluation.
L’aire $\mathscr{A}_{\lambda}$ correspond à l’aire du domaine situé entre la courbe $\mathscr{C}_u$, l’axe des abscisses et les droites d’équation $x=4$ et $x=\lambda$.
La fonction $u$ est continue et positive sur $[4;\lambda]$.
Ainsi :
$\begin{align*} \mathscr{A}_{\lambda}&=\int_4^{\lambda}u(x)\mathrm{d}x\phantom{\dfrac{1}{4}} \\\\ &=f(\lambda)-f(4) \\\\ &=f(\lambda)-\left(3-5\ln 4\right) \\\\ &=f(\lambda)-\dfrac{4}{\lambda}-3+5\ln 4 \end{align*}$
On veut donc résoudre l’équation $f(\lambda)-3+5\ln 4=5\ln 4 -6$
soit $f(\lambda)=-3$.
La fonction $f$ est continue (car dérivable) et strictement croissante sur $[4;+\infty[$.
De plus $f(4)=3-5\ln 4 <-3$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$
Par conséquent $-3\in [f(4);+\infty[$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l’équation $f(\lambda)=-3$ possède une unique solution.
$\quad$
Il existe donc une valeur de $\lambda$ telle que $\mathscr{A}=\mathscr{A}_{\lambda}$
$\quad$

 

Exercice 2 4 points

Commun à tous les candidats

 

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse.

Il est attribué un point par réponse exacte correctement justifiée. L'absence de réponse n'est pas pénalisée. Une réponse non justifiée n'est pas prise en compte.

L'espace est muni d'un repère orthonormé $(,O;\vec{i},\vec{j},\vec{k}\,)$. Les points A, B, C sont définis par leurs coordonnées : $$\text{A}(3;-1;4),\quad \text{B}(-1;2;-3),\quad \text{C}(4;-1;2).$$ Le plan $\mathcal{P}$ a pour équation cartésienne : $2x - 3y + 2z - 7 = 0$. La droite $\Delta$ a pour représentation paramétrique $\left\{\begin{array}{l c l} x &=& - 1 + 4t\\ y &=&\phantom{-} 4 - t\\ z &=& - 8 + 2t \end{array}\right., \:t \in \mathbb R$.

1. Affirmation 1 : Les droites $\Delta$ et (AC) sont orthogonales.
2. Affirmation 2 : Les points A, B et C déterminent un plan et ce plan a pour équation cartésienne $2x + 5y + z - 5 = 0$.
3. Affirmation 3 : Tous les points dont les coordonnées $(x;y;z)$ sont données par $\left\{\begin{array}{l c l} x &=& 1 + \phantom{2}s - 2s'\\ y &=& 1 - 2s + \phantom{2}s'\\ z &=& 1- 4s + 2s' \end{array}\right., \: s \in \mathbb R,\: s' \in \mathbb R$ appartiennent au plan $\mathcal{P}$.
4. Affirmation 4 : Il existe un plan parallèle au plan $\mathcal{P}$ qui contient la droite $\Delta$.

 

Correction de l'exercice 2 4 points

Commun à tous les candidats

 

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse.

Il est attribué un point par réponse exacte correctement justifiée. L'absence de réponse n'est pas pénalisée. Une réponse non justifiée n'est pas prise en compte.

L'espace est muni d'un repère orthonormé $(,O;\vec{i},\vec{j},\vec{k}\,)$. Les points A, B, C sont définis par leurs coordonnées : $$\text{A}(3;-1;4),\quad \text{B}(-1;2;-3),\quad \text{C}(4;-1;2).$$ Le plan $\mathcal{P}$ a pour équation cartésienne : $2x - 3y + 2z - 7 = 0$. La droite $\Delta$ a pour représentation paramétrique $\left\{\begin{array}{l c l} x &=& - 1 + 4t\\ y &=&\phantom{-} 4 - t\\ z &=& - 8 + 2t \end{array}\right., \:t \in \mathbb R$.

1. Affirmation 1 : Les droites $\Delta$ et (AC) sont orthogonales.
On a $\overrightarrow{AC}(1;0;-2)$.
Un vecteur directeur de $\Delta$ est $\vec{u}(4;-1;2)$.
Ainsi $\overrightarrow{AC}.\vec{u}=4+0-4=0$.
Les droites $\Delta$ et $(AC)$ sont donc orthogonales.
L’affirmation est vraie.
$\quad$
2. Affirmation 2 : Les points A, B et C déterminent un plan et ce plan a pour équation cartésienne $2x + 5y + z - 5 = 0$.
$\overrightarrow{AB}(-4;3;-7)$ et $\overrightarrow{AC}(1;0;-2)$
$\dfrac{1}{-4} \neq \dfrac{0}{3}$. Ces deux vecteurs ne sont donc pas colinéaires et les points $A$, $B$ et $C$ définissent un plan.
Regardons si les coordonnées des points $A, B$ et $C$ vérifient l’équation $2x+5y+z-5=0$.
$2\times 3+5\times (-1)+4-5 = 6-5+4-5=0 \checkmark$
$2\times (-1)+5\times 2-3-5=-2+10-3-5=0 \checkmark$
$2\times 4+5\times (-1)+2-5=8-5+2-5=0 \checkmark$
$2x+5y+z-5=0$ est donc une équation cartésienne du plan $(ABC)$.
L’affirmation est vraie.
$\quad$
3. Affirmation 3 : Tous les points dont les coordonnées $(x;y;z)$ sont données par $\left\{\begin{array}{l c l} x &=& 1 + \phantom{2}s - 2s'\\ y &=& 1 - 2s + \phantom{2}s'\\ z &=& 1- 4s + 2s' \end{array}\right., \: s \in \mathbb R,\: s' \in \mathbb R$ appartiennent au plan $\mathcal{P}$.
Regardons si les coordonnées données vérifient l’équation du plan $P$.
$2(1+s-2s’)-3(1-2s+s’)+2(1-4s+2s’)-7$ $=2+2s-4s’-3+6s-3s’+2-8s+4s’-7$ $= -6-3s’$.
Or $-6-3s’$ n’est pas toujours égal à $0$.
L’affirmation est fausse.
$\quad$
4. Affirmation 4 : Il existe un plan parallèle au plan $\mathcal{P}$ qui contient la droite $\Delta$.
Un vecteur normal à $P$ est $\vec{n}(2;-3;2)$.
Un vecteur directeur de $\Delta$ est $\vec{u}(4;-1;2)$.
$\vec{n}.\vec{u}=8+3+4=15 \neq 0$
La droite $\Delta$ ne peut donc pas appartenir à un plan parallèle à $P$.
L’affirmation est fausse.
$\quad$

 

Exercice 3 5 points

Probabilités

Les trois parties A, B et C peuvent être traitées de façon indépendante

Partie A

Le chikungunya est une maladie virale transmise d'un être humain à l'autre par les piqûres de moustiques femelles infectées.
Un test a été mis au point pour le dépistage de ce virus. Le laboratoire fabriquant ce test fournit les caractéristiques suivantes :

• la probabilité qu'une personne atteinte par le virus ait un test positif est de $0,98$ ;
• la probabilité qu'une personne non atteinte par le virus ait un test positif est de $0,01$.

On procède à un test de dépistage systématique dans une population «cible ». Un individu est choisi au hasard dans cette population. On appelle :

• $M$ l'évènement: «L'individu choisi est atteint du chikungunya »
• $T$ l'évènement: «Le test de l'individu choisi est positif »

On notera $\overline{M}$ (respectivement $\overline{T}$) l'évènement contraire de l'évènement $M$ (respectivement $T$). On note $p\: (0 \leqslant p \leqslant 1$) la proportion de personnes atteintes par la maladie dans la population cible.

1. 1. Recopier et compléter l'arbre de probabilité ci-dessous.
      
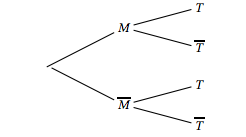
   2. Exprimer $P(M \cap T),\: P\left(\overline{M} \cap T\right)$ puis $P(T)$ en fonction de $p$.
2. 1. Démontrer que la probabilité de $M$ sachant $T$ est donnée par la fonction $f$ définie sur [0 ; 1] par : $$f(p) = \dfrac{98p}{97p+1}.$$
   2. Étudier les variations de la fonction $f$.
3. On considère que le test est fiable lorsque la probabilité qu'une personne ayant un test positif soit réellement atteinte du chikungunya est supérieure à $0,95$. En utilisant les résultats de la question \textbf{2.}, à partir de quelle proportion $p$ de malades dans la population le test est-il fiable ?

 

Partie B

En juillet 2014, l'institut de veille sanitaire d'une île, en s'appuyant sur les données remontées par les médecins, publie que 15 % de la population est atteinte par le virus. Comme certaines personnes ne consultent pas forcément leur médecin, on pense que la proportion est en réalité plus importante. Pour s'en assurer, on se propose d'étudier un échantillon de 1000 personnes choisies au hasard dans cette île. La population est suffisamment importante pour considérer qu'un tel échantillon résulte de tirages avec remise. On désigne par $X$ la variable aléatoire qui, à tout échantillon de 1000 personnes choisies au hasard, fait correspondre le nombre de personnes atteintes par le virus et par $F$ la variable aléatoire donnant la fréquence associée.

1. 1. Sous l'hypothèse $p = 0,15$, déterminer la loi de $X$.
   2. Dans un échantillon de 1000 personnes choisies au hasard dans l'île, on dénombre $197$ personnes atteintes par le virus. Quelle conclusion peut-on tirer de cette observation à propos du chiffre de 15 % publié par l'institut de veille sanitaire ? Justifier. (On pourra s'aider du calcul d'un intervalle de fluctuation au seuil de 95 %.)
2. On considère désormais que la valeur de $p$ est inconnue. En utilisant l'échantillon de la question 1. b. , proposer un intervalle de confiance de la valeur de $p$, au niveau de confiance de 95 %.

 

Partie C

Le temps d'incubation, exprimé en heures, du virus peut être modélisé par une variable aléatoire $T$ suivant une loi normale d'écart type $\sigma = 10$. On souhaite déterminer sa moyenne $\mu$. La représentation graphique de la fonction densité de probabilité de $T$ est donnée en annexe.

1. 1. Conjecturer, à l'aide du graphique, une valeur approchée de $\mu$.
   2. On donne $p(T < 110) = 0,18$. Hachurer sur le graphique un domaine dont l'aire correspond à la probabilité donnée.
2. On note $T'$ la variable aléatoire égale à $\dfrac{T - \mu}{10}$.
   1. Quelle loi la variable aléatoire $T'$ suit-elle ?
   2. Déterminer une valeur approchée à l'unité près de la moyenne $\mu$ de la variable aléatoire $T$ et vérifier la conjecture de la question 1.

 

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Les trois parties A, B et C peuvent être traitées de façon indépendante

Partie A

Le chikungunya est une maladie virale transmise d'un être humain à l'autre par les piqûres de moustiques femelles infectées.
Un test a été mis au point pour le dépistage de ce virus. Le laboratoire fabriquant ce test fournit les caractéristiques suivantes :

• la probabilité qu'une personne atteinte par le virus ait un test positif est de $0,98$ ;
• la probabilité qu'une personne non atteinte par le virus ait un test positif est de $0,01$.

On procède à un test de dépistage systématique dans une population «cible ». Un individu est choisi au hasard dans cette population. On appelle :

• $M$ l'évènement: «L'individu choisi est atteint du chikungunya »
• $T$ l'évènement: «Le test de l'individu choisi est positif »

On notera $\overline{M}$ (respectivement $\overline{T}$) l'évènement contraire de l'évènement $M$ (respectivement $T$). On note $p\: (0 \leqslant p \leqslant 1$) la proportion de personnes atteintes par la maladie dans la population cible.

1. 1. Recopier et compléter l'arbre de probabilité ci-dessous.
   
   
   2. Exprimer $P(M \cap T),\: P\left(\overline{M} \cap T\right)$ puis $P(T)$ en fonction de $p$.
   $P(M\cap T) = 0,98p$ $\quad$ $P\left(\overline{M} \cap T\right) = 0,01(1-p)$
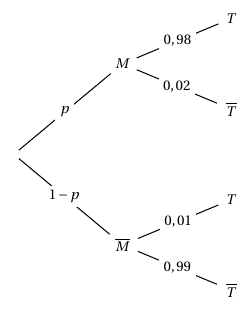
   D’après la formule des probabilités totales on a :
   $\begin{align*} P(T) &= P(M \cap T) + P\left(\overline{M} \cap T\right) \\\\ &= 0,98p + 0,01(1-p) \\\\ &=0,98p +0,01-0,01p\\\\ &=0,97p+0,01 \end{align*}$
2. 1. Démontrer que la probabilité de $M$ sachant $T$ est donnée par la fonction $f$ définie sur [0 ; 1] par : $$f(p) = \dfrac{98p}{97p+1}.$$
   On veut calculer
   $P_T(M)=\dfrac{P(M\cap T)}{P(T)}$ $= \dfrac{0,98p}{0,97p+0,01} = \dfrac{98p}{97p+1}$
   $\quad$
   
   2. Étudier les variations de la fonction $f$.
   La fonction $f$ est dérivable sur $[0;1]$ en tant que quotient de fonctions dérivables dont le dénominateur ne s’annule pas sur $[0;1]$
   $f'(p)=\dfrac{98(97p+1)-97\times 98p}{(97p+1)^2} = \dfrac{98}{(97p+1)^2} >0$.
   La fonction $f$ est donc strictement croissante sur $[0;1]$.
3. On considère que le test est fiable lorsque la probabilité qu'une personne ayant un test positif soit réellement atteinte du chikungunya est supérieure à $0,95$. En utilisant les résultats de la question \textbf{2.}, à partir de quelle proportion $p$ de malades dans la population le test est-il fiable ?
On veut résoudre l’inéquation :
$\begin{align*} f(p)> 0,95 &\Leftrightarrow \dfrac{98p}{97p+1} > 0,95 \\\\ &\Leftrightarrow 98p > 0,95(97p+1) \\\\ &\Leftrightarrow 98p>92,15p+0,95 \\\\ &\Leftrightarrow 5,85p>0,95 \\\\ &\Leftrightarrow p>\dfrac{0,95}{5,85} \\\\ &\Leftrightarrow p>\dfrac{19}{117} \end{align*}$

 

Partie B

En juillet 2014, l'institut de veille sanitaire d'une île, en s'appuyant sur les données remontées par les médecins, publie que 15 % de la population est atteinte par le virus. Comme certaines personnes ne consultent pas forcément leur médecin, on pense que la proportion est en réalité plus importante. Pour s'en assurer, on se propose d'étudier un échantillon de 1000 personnes choisies au hasard dans cette île. La population est suffisamment importante pour considérer qu'un tel échantillon résulte de tirages avec remise. On désigne par $X$ la variable aléatoire qui, à tout échantillon de 1000 personnes choisies au hasard, fait correspondre le nombre de personnes atteintes par le virus et par $F$ la variable aléatoire donnant la fréquence associée.

1. 1. Sous l'hypothèse $p = 0,15$, déterminer la loi de $X$.
   Les $1~000$ tirages sont indépendants, aléatoires avec remises et présentent chacun deux issues : $M$ et $\overline{M}$.
   De plus $P(M)=0,15$.
   $X$ suit donc la loi binomiale de paramètres $n=1~000$ et $p=0,15$.
   
   2. Dans un échantillon de 1000 personnes choisies au hasard dans l'île, on dénombre $197$ personnes atteintes par le virus. Quelle conclusion peut-on tirer de cette observation à propos du chiffre de 15 % publié par l'institut de veille sanitaire ? Justifier. (On pourra s'aider du calcul d'un intervalle de fluctuation au seuil de 95 %.)
   $n=1~000$ et $p=0,15$
   $n=1~000 \ge 30 \checkmark$ $\quad$ $np=150 \ge 5 \checkmark$ $\quad$ $n(1-p)=850 \ge 5 \checkmark$.
   Un intervalle de fluctuation asymptotique au seuil de $95\%$ est alors :
   $\begin{align*} I_{1~000} &= \left[0,15-1,96\sqrt{\dfrac{0,15 \times 0,85}{1~000}};0,15+ 1,96\sqrt{\dfrac{0,15 \times 0,85}{1~000}}\right] \\\\ &\approx [0,127;0,173] \end{align*}$
   La fréquence observée est $f=\dfrac{197}{1~000} = 0,197 \notin I_{1~000}$
   On peut donc remettre en cause le chiffre publié par l’institut de veille sanitaire.
   $\quad$
2. On considère désormais que la valeur de $p$ est inconnue. En utilisant l'échantillon de la question 1. b. , proposer un intervalle de confiance de la valeur de $p$, au niveau de confiance de 95 %.
$n=1~000 \ge 30 \checkmark$ $\quad$ $nf=197 \ge 5 \checkmark$ $\quad$ $n(1-f)=803 \ge 5 \checkmark$.
Un intervalle de confiance au seuil de confiance de $95\%$ est :
$\begin{align*} J_{1~000}&=\left[0,197-\dfrac{1}{\sqrt{1~000}};0,197+\dfrac{1}{\sqrt{1~000}}\right] \\\\ &\approx [0,165;0,229] \end{align*}$

 

Partie C

Le temps d'incubation, exprimé en heures, du virus peut être modélisé par une variable aléatoire $T$ suivant une loi normale d'écart type $\sigma = 10$. On souhaite déterminer sa moyenne $\mu$. La représentation graphique de la fonction densité de probabilité de $T$ est donnée en annexe.

1. 1. Conjecturer, à l'aide du graphique, une valeur approchée de $\mu$.
   D’après le graphique, on peut conjecturer que $\mu \approx 120$.
   
   2. On donne $p(T < 110) = 0,18$. Hachurer sur le graphique un domaine dont l'aire correspond à la probabilité donnée.
   
2. On note $T'$ la variable aléatoire égale à $\dfrac{T - \mu}{10}$.
   1. Quelle loi la variable aléatoire $T'$ suit-elle ?
   $T’$ suit la loi normale centrée réduite.
   $\quad$
   
   2. Déterminer une valeur approchée à l'unité près de la moyenne $\mu$ de la variable aléatoire $T$ et vérifier la conjecture de la question 1.
   $\begin{align*} p(T<110)=0,18 &\Leftrightarrow p(T-\mu<110-\mu)=0,18 \\\\ &\Leftrightarrow p\left(\dfrac{T-\mu}{10}<\dfrac{110-\mu}{10}\right) = 0,18 \\\\ &\Leftrightarrow p\left(T'<\dfrac{110-\mu}{10}\right) = 0,18 \end{align*}$
   En utilisant la calculatrice, on trouve que $\dfrac{110-\mu}{10}\approx -0,915$ soit $\mu \approx 119$.
   Cette valeur est très proche de celle conjecturée à la question 1. $\quad$

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Dans un pays de population constante égale à 120 millions, les habitants vivent soit en zone rurale, soit en ville. Les mouvements de population peuvent être modélisés de la façon suivante :

• en 2010, la population compte $90$ millions de ruraux et $30$ millions de citadins ;
• chaque année, 10 % des ruraux émigrent à la ville ;
• chaque année, 5 % des citadins émigrent en zone rurale.

Pour tout entier naturel $n$, on note :

• $u_n$ la population en zone rurale, en l'année $2010 + n$, exprimée en millions d'habitants ;
• $v_n$ la population en ville, en l'année $2010 + n$, exprimée en millions d'habitants.

On a donc $u_0 = 90$ et $v_0 = 30$.

Partie A

 

1. Traduire le fait que la population totale est constante par une relation liant $u_n$ et $v_n$.
2. On utilise un tableur pour visualiser l'évolution des suites $\left(u_n\right)$ et $\left(v_n\right)$. Quelles formules peut-on saisir dans les cellules B3 et C3 qui, recopiées vers le bas, permettent d'obtenir la feuille de calcul ci-dessous : $$\begin{array} {|c|c|c|c|}\hline &A &B&C\\ \hline 1&n &\text{ Population en zone rurale }&\text{ Population en ville }\\ \hline 2&0 &90 &30\\ \hline 3&1 &82,5 &37,5\\ \hline 4&2 &76,125 &43,875\\ \hline 5&3 &70,706 &49,294\\ \hline 6&4 &66,100 &53,900\\ \hline 7&5 &62,185 &57.815\\ \hline 8&6 &58,857 &61,143\\ \hline 9&7 &56,029 &63,971\\ \hline 10&8&53,625 &66,375\\ \hline 11&9&51,581 &68,419\\ \hline 12&10&49,844 &70,156\\ \hline 13&11&48,367 &71,633\\ \hline 14&12&47,112 &72,888\\ \hline 15&13&46,045 &73,955\\ \hline 16&14&45,138 &74,862\\ \hline 17&15&44,368 &75,632\\ \hline 18&16&43,713 &76,287\\ \hline 19&17&43,156 &76,844\\ \hline 20&18&42,682 &77,318\\ \hline 21&19&42,280 &77,720\\ \hline 22&20&41,938 &78,062\\ \hline \ldots&\ldots&\ldots&\ldots\\\hline 59&57 &40,005 &79,995\\ \hline 60&58 &40,004 &79,996\\ \hline 61&59 &40,003 &79,997\\ \hline 62&60 &40,003 &79,997\\ \hline 63&61 &40,002 &79,998\\ \hline \end{array}$$
3. Quelles conjectures peut-on faire concernant l'évolution à long terme de cette population ?

 

Partie B

On admet dans cette partie que, pour tout entier naturel $n,\quad u_{n+1} = 0,85u_n + 6$.

1. 1. Démontrer par récurrence que la suite $\left(u_n\right)$ est décroissante.
   2. On admet que $u_n$ est positif pour tout entier naturel $n$. Que peut-on en déduire quant à la suite $\left(u_n\right)$ ?
2. On considère la suite $\left(w_n\right)$, définie par : $w_n = u_n - 40$, pour tout $n \geqslant 0$.
   1. Démontrer que $\left(w_n\right)$ est une suite géométrique de raison $0,85$.
   2. En déduire l'expression de $w_n$ puis de $u_n$ en fonction de $n$.
   3. Déterminer l'expression de $v_n$ en fonction de $n$.
3. Valider ou invalider les conjectures effectuées à la question \textbf{3.} de la \textbf{partie A}.
4. On considère l'algorithme suivant : $$\begin{array}{|c|c|}\hline \text{Entrée :} & n \text{ et } u \text{sont des nombres }\\\hline \text{Initialisation :}&n \text{ prend la valeur } 0\\ \hline &u \text{ prend la valeur } 90\\ \text{Traitement :} &\text{Tant que } u \geqslant 120 - u \text{ faire }\\\hline &\hspace{0.75cm}n \text{ prend la valeur }n + 1\\ &\hspace{0.75cm}u \text{ prend la valeur } 0,85 \times u + 6\\ &\text{ Fin Tant que }\\ \text{ Sortie : } &\text{Afficher } n \\ \hline \end{array}$$
   1. Que fait cet algorithme ?
   2. Quelle valeur affiche-t-il ?

 

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Dans un pays de population constante égale à 120 millions, les habitants vivent soit en zone rurale, soit en ville. Les mouvements de population peuvent être modélisés de la façon suivante :

• en 2010, la population compte $90$ millions de ruraux et $30$ millions de citadins ;
• chaque année, 10 % des ruraux émigrent à la ville ;
• chaque année, 5 % des citadins émigrent en zone rurale.

Pour tout entier naturel $n$, on note :

• $u_n$ la population en zone rurale, en l'année $2010 + n$, exprimée en millions d'habitants ;
• $v_n$ la population en ville, en l'année $2010 + n$, exprimée en millions d'habitants.

On a donc $u_0 = 90$ et $v_0 = 30$.

Partie A

 

1. Traduire le fait que la population totale est constante par une relation liant $u_n$ et $v_n$.
On a $u_n+v_n=120$ pour tout entier naturel $n$.

2. On utilise un tableur pour visualiser l'évolution des suites $\left(u_n\right)$ et $\left(v_n\right)$. Quelles formules peut-on saisir dans les cellules B3 et C3 qui, recopiées vers le bas, permettent d'obtenir la feuille de calcul ci-dessous : $$\begin{array} {|c|c|c|c|}\hline &A &B&C\\ \hline 1&n &\text{ Population en zone rurale }&\text{ Population en ville }\\ \hline 2&0 &90 &30\\ \hline 3&1 &82,5 &37,5\\ \hline 4&2 &76,125 &43,875\\ \hline 5&3 &70,706 &49,294\\ \hline 6&4 &66,100 &53,900\\ \hline 7&5 &62,185 &57.815\\ \hline 8&6 &58,857 &61,143\\ \hline 9&7 &56,029 &63,971\\ \hline 10&8&53,625 &66,375\\ \hline 11&9&51,581 &68,419\\ \hline 12&10&49,844 &70,156\\ \hline 13&11&48,367 &71,633\\ \hline 14&12&47,112 &72,888\\ \hline 15&13&46,045 &73,955\\ \hline 16&14&45,138 &74,862\\ \hline 17&15&44,368 &75,632\\ \hline 18&16&43,713 &76,287\\ \hline 19&17&43,156 &76,844\\ \hline 20&18&42,682 &77,318\\ \hline 21&19&42,280 &77,720\\ \hline 22&20&41,938 &78,062\\ \hline \ldots&\ldots&\ldots&\ldots\\\hline 59&57 &40,005 &79,995\\ \hline 60&58 &40,004 &79,996\\ \hline 61&59 &40,003 &79,997\\ \hline 62&60 &40,003 &79,997\\ \hline 63&61 &40,002 &79,998\\ \hline \end{array}$$
En $B3$ on peut saisir : $=B2*0,9+C2*0,05$ et en $C3$ : $=B2*0,1+C2*0,95$
$\quad$
3. Quelles conjectures peut-on faire concernant l'évolution à long terme de cette population ?
On peut conjecturer que la suite $\left(u_n\right)$ est décroissante, la suite $\left(v_n\right)$ est croissante et que sur le long terme, il y aura $40$ millions de ruraux et $80$ millions de citadins.
$\quad$

 

Partie B

On admet dans cette partie que, pour tout entier naturel $n,\quad u_{n+1} = 0,85u_n + 6$.

1. 1. Démontrer par récurrence que la suite $\left(u_n\right)$ est décroissante.
   Initialisation : Si $n=0$, $u_0=90$ et $u_1=82,5$
   On a bien $u_1<u_0$. La suite est décroissante.
   La propriété est vraie au rang $0$.
   $\quad$
   Hérédité : Supposons la propriété vraie au rang $n$ : $u_{n+1} \le u_n$ soit $u_{n+1}-u_n \le 0$
   $\begin{align*} u_{n+2}-u_{n+1} &= 0,85u_{n+1}+6-\left(0,85u_n+6\right) \\\\ &=0,85u_{n+1}-0,85u_n \\\\ &=0,85\left(u_{n+1}-u_n\right)\\\\ &\le 0 \end{align*}$
   Par conséquent la propriété est vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Par conséquent, pour tout entier naturel $u_{n+1} \le u_n$ et la suite $\left(u_n\right)$ est décroissante.
   $\quad$
   
   2. On admet que $u_n$ est positif pour tout entier naturel $n$. Que peut-on en déduire quant à la suite $\left(u_n\right)$ ?
   La suite $\left(u_n\right)$ est décroissante et minorée par $0$. Elle est donc convergente.
   $\quad$
2. On considère la suite $\left(w_n\right)$, définie par : $w_n = u_n - 40$, pour tout $n \geqslant 0$.
   1. Démontrer que $\left(w_n\right)$ est une suite géométrique de raison $0,85$.
   $\begin{align*} w_{n+1} &=u_{n+1}-40 \\\\ &=0,85u_n+6-40 \\\\ &=0,85u_n-34\\\\ &=0,85u_n-0,85\times 40\\\\ &=0,85\left(u_n-40\right) \\\\ &=0,85w_n \end{align*}$
   La suite $\left(w_n\right)$ est donc géométrique de raison $0,85$ et de premier terme $w_0=u_0-40=50$.
   $\quad$
   
   2. En déduire l'expression de $w_n$ puis de $u_n$ en fonction de $n$.
   On a donc $w_n=50\times 0,85^n$.
   Or $u_n=w_n+40$ donc $u_n = 40+50\times 0,85^n$.
   $\quad$
   
   3. Déterminer l'expression de $v_n$ en fonction de $n$.
   Puisque $u_n+v_n=120$ on a alors $v_n=120-u_n = 80-50\times 0,85^n$.
   $\quad$
   La suite $\left(u_n\right)$ est bien décroissante et la suite $\left(v_n\right)$, du fait que la population est constante, est croissante.
   $0<0,85<1$ donc $\lim\limits_{n \to +\infty} 0,85^n=0$ donc $\lim\limits_{n \to +\infty} u_n=40$ et $\lim\limits_{n \to +\infty} v_n=80$.
   Les conjectures faites à la partie A sont donc validées.
3. Valider ou invalider les conjectures effectuées à la question \textbf{3.} de la \textbf{partie A}.
4. On considère l'algorithme suivant : $$\begin{array}{|c|c|}\hline \text{Entrée :} & n \text{ et } u \text{sont des nombres }\\\hline \text{Initialisation :}&n \text{ prend la valeur } 0\\ \hline &u \text{ prend la valeur } 90\\ \text{Traitement :} &\text{Tant que } u \geqslant 120 - u \text{ faire }\\\hline &\hspace{0.75cm}n \text{ prend la valeur }n + 1\\ &\hspace{0.75cm}u \text{ prend la valeur } 0,85 \times u + 6\\ &\text{ Fin Tant que }\\ \text{ Sortie : } &\text{Afficher } n \\ \hline \end{array}$$
   1. Que fait cet algorithme ?
   La boucle s’arrête quand $u \le 120-u$ soit $u<v$.
   Cet algorithme détermine donc le nombre d’années nécessaires pour que la population rurale soit inférieure à la population citadine
   
   2. Quelle valeur affiche-t-il ?
   D’après la feuille de calcul, l’algorithme affiche $6$

 

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Dans un pays de population constante égale à 120 millions, les habitants vivent soit en zone rurale, soit en ville. Les mouvements de population peuvent être modélisés de la façon suivante :

• en 2010, la population compte $90$ millions de ruraux et $30$ millions de citadins ;
• chaque année, 10 % des ruraux émigrent à la ville;
• chaque année, 5 % des citadins émigrent en zone rurale.

Pour tout entier naturel $n$, on note :

• $R_n$ l'effectif de la population rurale, exprimé en millions d'habitants, en l'année $2010 + n$,
• $C_n$ l'effectif de la population citadine, exprimé en millions d'habitants, en l'année $2010+n$.

On a donc $R_0 = 90$ et $C_0 = 30$.

1. On considère les matrices $M = \begin{pmatrix}0,9& 0,05\\0,1& 0,95\end{pmatrix}$ et, pour tout entier naturel $n,$ $U_n = \begin{pmatrix}R_n\\C_n \end{pmatrix}$.
   1. Démontrer que, pour tout entier naturel $n,\: U_{n+1} = MU_n$.
   2. Calculer $U_1$. En déduire le nombre de ruraux et le nombre de citadins en 2011.
2. Pour tout entier naturel $n$ non nul, exprimer $U_n$ en fonction de $M^n$ et de $U_0$.
3. Soit la matrice $P = \begin{pmatrix}1&1\\2&- 1 \end{pmatrix}$. Montrer que la matrice  $\begin{pmatrix}\dfrac{1}{3}&\dfrac{1}{3}\\\dfrac{2}{3}&-\dfrac{1}{3}\end{pmatrix}$ est la matrice inverse de $P$ et on la notera $P^{-1}$.
4. 1. On pose $\Delta = P^{-1}MP$. Calculer $\Delta$ à l'aide de la calculatrice.
   2. Démontrer que : $M = P\Delta P^{-1}$.
   3. Démontrer par récurrence que, pour tout entier naturel $n$ non nul: $$M^n = P\Delta^nP^{-1}.$$
5. 1. On admet que le calcul matriciel précédent donne : $$M^n = \begin{pmatrix}\dfrac{1}{3} + \dfrac{2}{3} \times 0,85^n&\dfrac{1}{3} - \dfrac{1}{3} \times 0,85^n\\\dfrac{2}{3} - \dfrac{2}{3} \times 0,85^n&\dfrac{2}{3} + \dfrac{1}{3} \times 0,85^n\end{pmatrix}.$$ En déduire que, pour tout entier naturel $n$, $R_n = 50 \times 0,85^n + 40$ et déterminer l'expression de $C_n$ en fonction de $n$.
   2. Déterminer la limite de $R_n$ et de $C_n$ lorsque $n$ tend vers $+ \infty$. Que peut-on en conclure pour la population étudiée ?
6. 1. On admet que $\left(R_n\right)$ est décroissante et que $\left(C_n\right)$ est croissante. Compléter l'algorithme donné en annexe afin qu'il affiche le nombre d'années au bout duquel la population urbaine dépassera la population rurale.
   2. En résolvant l'inéquation d'inconnue $n, 50 \times 0,85^n + 40 < 80 - 50 \times 0,85^n$, retrouver la valeur affichée par l'algorithme.

 

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Dans un pays de population constante égale à 120 millions, les habitants vivent soit en zone rurale, soit en ville. Les mouvements de population peuvent être modélisés de la façon suivante :

• en 2010, la population compte $90$ millions de ruraux et $30$ millions de citadins ;
• chaque année, 10 % des ruraux émigrent à la ville;
• chaque année, 5 % des citadins émigrent en zone rurale.

Pour tout entier naturel $n$, on note :

• $R_n$ l'effectif de la population rurale, exprimé en millions d'habitants, en l'année $2010 + n$,
• $C_n$ l'effectif de la population citadine, exprimé en millions d'habitants, en l'année $2010+n$.

On a donc $R_0 = 90$ et $C_0 = 30$.

1. On considère les matrices $M = \begin{pmatrix}0,9& 0,05\\0,1& 0,95\end{pmatrix}$ et, pour tout entier naturel $n,$ $U_n = \begin{pmatrix}R_n\\C_n \end{pmatrix}$.
   1. Démontrer que, pour tout entier naturel $n,\: U_{n+1} = MU_n$.
   Chaque année $90\%$ des ruraux restent à la campagne et $95\%$ des citadins restent à la ville.
   Ainsi, pour tout entier naturel $n$, on a $R_{n+1}=0,9R_n+0,05C_n$ et $C_{n+1}=0,10R_n+0,95C_n$.
   $MU_{n}=\begin{pmatrix} 0,9R_n+0,05C_n\\\\0,1R_n+0,95C_n\end{pmatrix}=U_{n+1}$
   $\quad$
   
   2. Calculer $U_1$. En déduire le nombre de ruraux et le nombre de citadins en 2011.
   $U_1=\begin{pmatrix} 0,9\times 90+0,05\times 30\\\\0,1 \times 90 + 0,95 \times 30\end{pmatrix} = \begin{pmatrix} 82,5\\\\37,5\end{pmatrix}$
   $\quad$
   En 2011, il y avait donc $82,5$ millions de ruraux et $37,5$ millions de citadins.
   $\quad$
2. Pour tout entier naturel $n$ non nul, exprimer $U_n$ en fonction de $M^n$ et de $U_0$.
Puisque $U_{n+1}=MU_n$ alors on a $U_n=M^nU_0$.
$\quad$
3. Soit la matrice $P = \begin{pmatrix}1&1\\2&- 1 \end{pmatrix}$. Montrer que la matrice $\begin{pmatrix}\dfrac{1}{3}&\dfrac{1}{3}\\\dfrac{2}{3}&-\dfrac{1}{3}\end{pmatrix}$ est la matrice inverse de $P$ et on la notera $P^{-1}$.
$\begin{pmatrix}1&1\\2&-1\end{pmatrix} \times \begin{pmatrix}\dfrac{1}{3}&\dfrac{1}{3}\\\\\dfrac{2}{3}&-\dfrac{1}{3}\end{pmatrix} = \begin{pmatrix}\dfrac{1}{3}+\dfrac{2}{3}&\dfrac{1}{3}-\dfrac{1}{3}\\\\\dfrac{2}{3}-\dfrac{2}{3}&\dfrac{2}{3}-\dfrac{1}{3}\end{pmatrix} = I_2$
où $I_2$ est la matrice identité d’ordre $2$
La matrice $P$ est donc inversible et son inverse est la matrice $\begin{pmatrix}\dfrac{1}{3}&\dfrac{1}{3}\\\\\dfrac{2}{3}&-\dfrac{1}{3}\end{pmatrix}$.
$\quad$
4. 1. On pose $\Delta = P^{-1}MP$. Calculer $\Delta$ à l'aide de la calculatrice.
   A l’aide de la calculatrice, on trouve $\Delta = \begin{pmatrix}1&0&\\0&0,85\end{pmatrix}$.
   $\quad$
   
   2. Démontrer que : $M = P\Delta P^{-1}$.
   $\Delta=P^{-1}MP \Leftrightarrow P\Delta=MP \Leftrightarrow P\Delta P^{-1}=M$
   $\quad$
   
   3. Démontrer par récurrence que, pour tout entier naturel $n$ non nul: $$M^n = P\Delta^nP^{-1}.$$
   Initialisation : Si $n=1$, d’après la question précédente, $M=P\Delta P^{-1}$.
   La propriété est vraie au rang $1$.
   $\quad$
   Hérédité : On suppose la propriété vraie au rang $n$ : $M^n=P\Delta^n P^{-1}$.
   $M^{n+1}=M^nM=P \Delta^n P^{-1}P\Delta P^{-1} = P\Delta^n \Delta P^{-1} = P\Delta^{n+1} P^{-1}$
   La propriété est donc vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$ non nul, on a $M^n=P\Delta^n P^{-1}$.
5. 1. On admet que le calcul matriciel précédent donne : $$M^n = \begin{pmatrix}\dfrac{1}{3} + \dfrac{2}{3} \times 0,85^n&\dfrac{1}{3} - \dfrac{1}{3} \times 0,85^n\\\dfrac{2}{3} - \dfrac{2}{3} \times 0,85^n&\dfrac{2}{3} + \dfrac{1}{3} \times 0,85^n\end{pmatrix}.$$ En déduire que, pour tout entier naturel $n$, $R_n = 50 \times 0,85^n + 40$ et déterminer l'expression de $C_n$ en fonction de $n$.
   On a $U_n=M^nU_0$ donc $U_n=\begin{pmatrix} 30+60\times 0,85^n+10-10\times 0,85^n\\\\60-60\times 0,85^n+20+10\times 0,85^n\end{pmatrix} = \begin{pmatrix} 40+50\times 0,85^n\\80-50\times 0,85^n\end{pmatrix}$
   On a donc $R_n=50\times 0,85^n+40$ et $C_n=80-50\times 0,85^n$.
   $\quad$
   
   2. Déterminer la limite de $R_n$ et de $C_n$ lorsque $n$ tend vers $+ \infty$. Que peut-on en conclure pour la population étudiée ?
   $0<0,85<1$ donc $\lim\limits_{n \to +\infty} 0,85^n=0$ donc $\lim\limits_{n \to +\infty} R_n=50$ et $\lim\limits_{n \to +\infty} C_n=80$.
   $\quad$
6. 1. On admet que $\left(R_n\right)$ est décroissante et que $\left(C_n\right)$ est croissante. Compléter l'algorithme donné en annexe afin qu'il affiche le nombre d'années au bout duquel la population urbaine dépassera la population rurale.
   Entrée :
   $\quad$ $n, R$ et $C$ sont des nombres
   Initialisation :
   $\quad$ $n$ prend la valeur $0$
   $\quad$ $R$ prend la valeur $90$
   $\quad$ $C$ prend la valeur $30$
   Traitement :
   $\quad$ Tant que $R\ge C$ faire
   $\qquad$ $n$ prend la valeur $n+1$
   $\qquad$ $R$ prend la valeur $50\times 0,85^n+40$
   $\qquad$ $C$ prend la valeur $120-R$
   $\quad$ Fin Tant que
   Sortie :
   $\quad$ Afficher $n$
   $\quad$
   
   2. En résolvant l'inéquation d'inconnue $n, 50 \times 0,85^n + 40 < 80 - 50 \times 0,85^n$, retrouver la valeur affichée par l'algorithme.
   $\begin{align*} 50\times 0,85^n+40<80-50\times 0,85^n &\Leftrightarrow 100\times 0,85^n<40 \\\\ &\Leftrightarrow 0,85^n < 0,4 \\\\ &\Leftrightarrow n \ln 0,85 < \ln 0,4 \\\\ &\Leftrightarrow n > \dfrac{\ln 0,4}{\ln 0,85}\\\\ & \Leftrightarrow n>6 \end{align*}$
   L’algorithme affichera donc $6$.