Baccalauréat S Polynésie 14 juin 2017
Exercice 1 6 points
La société Fibration fournit des abonnements Internet et des abonnements de téléphone mobile. Un client de la société Fibration souscrit soit un abonnement Internet, soit un abonnement de téléphone mobile, il ne cumule pas les deux. En cas de difficulté, la société Fibration propose à ses clients une ligne d'assistance téléphonique : le client doit d'abord signaler s'il est client Internet ou s'il est client mobile puis son appel est mis en attente de réponse par un opérateur.
Les parties A, B et C sont indépendantes.Si nécessaire, les résultats seront arrondis à $10^{-3}$.
Partie A - Durée d'attente
- Dans cette question, on s'intéresse à la durée d'attente d'un client Internet lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. Une étude permet de modéliser cette durée d'attente en minutes par la variable aléatoire $D_1$ qui suit la loi exponentielle de paramètre $0,6$.
- Quelle est la durée d'attente moyenne que peut espérer un client Internet qui appelle cette ligne d'assistance ?
- Calculer la probabilité que la durée d'attente d'un client Internet choisi au hasard soit inférieure à $5$ minutes.
- Dans cette question, on s'intéresse à la durée d'attente d'un client mobile lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. On modélise cette durée d'attente en minutes par la variable aléatoire $D_2$ qui suit une loi exponentielle de paramètre $\lambda$,\: $\lambda$ étant un réel strictement positif.
- Sachant que $P\left(D_2 \leqslant 4\right) = 0,798$, déterminer la valeur de $\lambda$.
- En prenant $\lambda = 0,4$, peut-on considérer que moins de 10 % des clients mobile choisis au hasard attendent plus de 5 minutes avant de joindre un opérateur ?
Partie B - Obtention d'un opérateur
Si la durée d'attente avant l'obtention d'un opérateur dépasse 5 minutes, l'appel prend automatiquement fin. Sinon, l'appelant obtient un opérateur. On çhoisit au hasard un client qui appelle la ligne d'assistance. On admet que la probabilité que l'appel émane d'un client Internet est $0,7$. De plus, d'après la partie A, on prend les données suivantes : Si l'appel provient d'un client Internet alors la probabilité d'obtenir un opérateur est égale à $0,95$. Si l'appel provient d'un client mobile alors la probabilité d'obtenir un opérateur est égale à $0,87$.
- Déterminer la probabilité que le client joigne un opérateur.
- Un client se plaint que son appel a pris fin après $5$ minutes d'attente sans avoir obtenu d'opérateur. Est-il plus probable que ce soit un client Internet ou un client mobile ?
Partie C - Enquête de satisfaction
La société annonce un taux de satisfaction de 85 % pour ses clients ayant appelé et obtenu un opérateur. Une association de consommateurs souhaite vérifier ce taux et interroge 1303 personnes. Parmi celles-ci, 1150 se disent satisfaites. Que pensez-vous du taux de satisfaction annoncé par la société ?
Correction de l'exercice 1 (6 points)
La société Fibration fournit des abonnements Internet et des abonnements de téléphone mobile. Un client de la société Fibration souscrit soit un abonnement Internet, soit un abonnement de téléphone mobile, il ne cumule pas les deux. En cas de difficulté, la société Fibration propose à ses clients une ligne d'assistance téléphonique : le client doit d'abord signaler s'il est client Internet ou s'il est client mobile puis son appel est mis en attente de réponse par un opérateur.
Les parties A, B et C sont indépendantes.Si nécessaire, les résultats seront arrondis à $10^{-3}$.
Partie A - Durée d'attente
- Dans cette question, on s'intéresse à la durée d'attente d'un client Internet lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. Une étude permet de modéliser cette durée d'attente en minutes par la variable aléatoire $D_1$ qui suit la loi exponentielle de paramètre $0,6$.
- Quelle est la durée d'attente moyenne que peut espérer un client Internet qui appelle cette ligne d'assistance ? La variable aléatoire $D_1$ suit la loi exponentielle de paramètre $0,6$.
- Calculer la probabilité que la durée d'attente d'un client Internet choisi au hasard soit inférieure à $5$ minutes. On veut calculer :
Par conséquent $E\left(D_1\right)=\dfrac{1}{0,6}\approx 1,667$
Le temps d’attente moyen est d’environ $1,667$ minutes soit environ $1$minute $40,02$ secondes.
$\quad$
$$\begin{array}{rl} P\left(D_1\leqslant 5\right)&=1-\text{e}^{-0,6\times 5} \\
&=1-\text{e}^{-3}\\
&\approx 0,950
\end{array}$$
La probabilité que la durée d’attente d’un client Internet choisi au hasard soit inférieure à $5$ minutes est environ $0,950$.
$\quad$ - Dans cette question, on s'intéresse à la durée d'attente d'un client mobile lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. On modélise cette durée d'attente en minutes par la variable aléatoire $D_2$ qui suit une loi exponentielle de paramètre $\lambda$,\: $\lambda$ étant un réel strictement positif.
- Sachant que $P\left(D_2 \leqslant 4\right) = 0,798$, déterminer la valeur de $\lambda$. La variable aléatoire $D_2$ suit une loi exponentielle de paramètre $\lambda$.
- En prenant $\lambda = 0,4$, peut-on considérer que moins de 10 % des clients mobile choisis au hasard attendent plus de 5 minutes avant de joindre un opérateur ? $P\left(D_2\geqslant 5\right)=\text{e}^{-0,4\times 5} \approx 0,135 > 0,1$.
$\begin{align*} P\left(D_2\leqslant 4\right)=0,798 &\iff 1-\text{e}^{-4\lambda}=0,798 \\
&\iff -\text{e}^{-4\lambda}=0,798-1\\
&\iff \text{e}^{-4\lambda}=0,202 \\
&\iff -4\lambda = \ln (0,202) \\
&\iff \lambda =\dfrac{\ln(0,202)}{-4}
\end{align*}$
$\quad$
On peut donc pas considérer que moins de $10\%$ des clients mobile choisis au hasard attendent plus de $5$ minutes avant de joindre un opérateur.
$\quad$
Partie B - Obtention d'un opérateur
Si la durée d'attente avant l'obtention d'un opérateur dépasse 5 minutes, l'appel prend automatiquement fin. Sinon, l'appelant obtient un opérateur. On çhoisit au hasard un client qui appelle la ligne d'assistance. On admet que la probabilité que l'appel émane d'un client Internet est $0,7$. De plus, d'après la partie A, on prend les données suivantes : Si l'appel provient d'un client Internet alors la probabilité d'obtenir un opérateur est égale à $0,95$. Si l'appel provient d'un client mobile alors la probabilité d'obtenir un opérateur est égale à $0,87$.
- Déterminer la probabilité que le client joigne un opérateur. On appelle :
- Un client se plaint que son appel a pris fin après $5$ minutes d'attente sans avoir obtenu d'opérateur. Est-il plus probable que ce soit un client Internet ou un client mobile ? On a : $p\left(\overline{A}\right)=1-0,926=0,074$
– $I$ l’événement “L’appel provient d’un client Internet”;
– $M$ l’événement “l’appel provient d’un client mobile”;
– $A$ le client a joint un opérateur de l’assistance téléphonique.
On obtient ainsi l’arbre pondéré suivant :
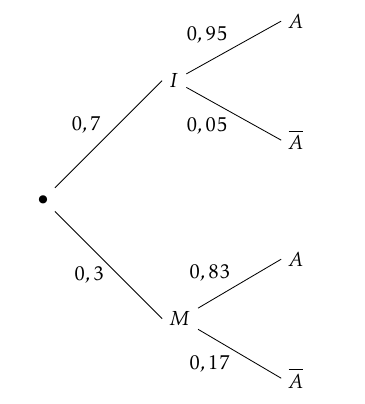
D’après la formule des probabilités totale, on a :
$\begin{align*} p(A)&=p(I\cap A)+p(M\cap A) \\
&=0,7\times 0,95+0,3\times 0,87 \\
&=0,926
\end{align*}$
La probabilité que le client joigne un opérateur est $0,926$.
$\begin{align*} p_{\overline{A}}(M)&=\dfrac{p\left(\overline{A}\cap M\right)} {p\left(\overline{A}\right)} \\
&=\dfrac{0,3\times 0,13}{0,074}\\
&\approx 0,527
\end{align*}$
et
$\begin{align*} p_{\overline{A}}(I)&=\dfrac{p\left(\overline{A}\cap I\right)} {p\left(\overline{A}\right)} \\
&=\dfrac{0,7\times 0,05}{0,074}\\
&\approx 0,473
\end{align*}$
On constate donc que $p_{\overline{A}}(M) > p_{\overline{A}}(I)$.
Il est donc plus probable que ce soit un client mobile.
$\quad$
Partie C - Enquête de satisfaction
On a $n=1~303 \geqslant 30$ et $p=0,85$ donc $np=1~107,55\geqslant 5$ et $n(1-p)=195,45\geqslant 5$
Un intervalle de fluctuation asymptotique au niveau de confiance de $95\%$ est :
$\begin{align*} I_{1~303}&=\left[0,85-1,96\sqrt{\dfrac{0,85\times 0,15}{1~303}};0,85+1,96\sqrt{\dfrac{0,85\times 0,15}{1~303}}\right] \\
&\approx [0,830;0,869]
\end{align*}$
La fréquence observée est $f=\dfrac{1~150}{1~303} \notin I_{1~303}$.
Cela remet en cause l’annonce de la société au risque de $5\%$.
Le taux de satisfaction de l’échantillon est cependant supérieur à celui annoncé par la société.
$\quad$
Exercice 2 5 points
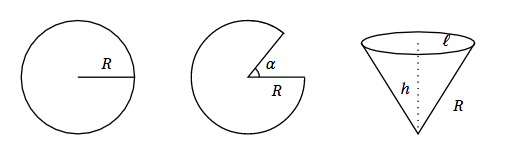
Dans un disque en carton de rayon $R$ , on découpe un secteur angulaire correspondant à un angle de mesure $\alpha$ radians. On superpose les bords afin de créer un cône de révolution. On souhaite choisir l'angle $\alpha$ pour obtenir un cône de volume maximal.
On appelle $\ell$ le rayon de la base circulaire de ce cône et $h$ sa hauteur. On rappelle que :
- le volume d'un cône de révolution de base un disque d'aire $\mathscr{A}$ et de hauteur $h$ est $\dfrac{1}{3}\mathscr{A}h$.
- la longueur d'un arc de cercle de rayon $r$ et d'angle $\theta$, exprimé en radians, est $r\theta$.
- On choisit $R = 20$ cm.
- Montrer que le volume du cône, en fonction de sa hauteur $h$, est $V(h) = \dfrac{1}{3}\pi\left(400-h^2\right)h$.
- Justifier qu'il existe une valeur de $h$ qui rend le volume du cône maximum. Donner cette valeur.
- Comment découper le disque en carton pour avoir un volume maximum ? Donner un arrondi de $\alpha$ au degré près.
- L'angle $\alpha$ dépend-il du rayon $R$ du disque en carton ?
Correction de l'exercice 2 (5 points)
Dans un disque en carton de rayon $R$ , on découpe un secteur angulaire correspondant à un angle de mesure $\alpha$ radians. On superpose les bords afin de créer un cône de révolution. On souhaite choisir l'angle $\alpha$ pour obtenir un cône de volume maximal.
On appelle $\ell$ le rayon de la base circulaire de ce cône et $h$ sa hauteur. On rappelle que :
- le volume d'un cône de révolution de base un disque d'aire $\mathscr{A}$ et de hauteur $h$ est $\dfrac{1}{3}\mathscr{A}h$.
- la longueur d'un arc de cercle de rayon $r$ et d'angle $\theta$, exprimé en radians, est $r\theta$.
- On choisit $R = 20$ cm.
- Montrer que le volume du cône, en fonction de sa hauteur $h$, est $V(h) = \dfrac{1}{3}\pi\left(400-h^2\right)h$.
- Justifier qu'il existe une valeur de $h$ qui rend le volume du cône maximum. Donner cette valeur.
- Comment découper le disque en carton pour avoir un volume maximum ? Donner un arrondi de $\alpha$ au degré près.
- L'angle $\alpha$ dépend-il du rayon $R$ du disque en carton ?
Exercice 3 4 points
Les interactions électriques conduisent à modéliser la molécule de méthane CH$_4$ de la façon suivante :
- Les noyaux d'atomes d'hydrogène occupent les positions des quatre sommets d'un tétraèdre régulier.
- Le noyau de carbone au centre de la molécule est à égale distance des quatre atomes d'hydrogène.
L'objectif est de déterminer une mesure de l'angle entre deux liaisons carbone--hydrogène. Un tétraèdre régulier est un polyèdre dont les quatre faces sont des triangles équilatéraux.
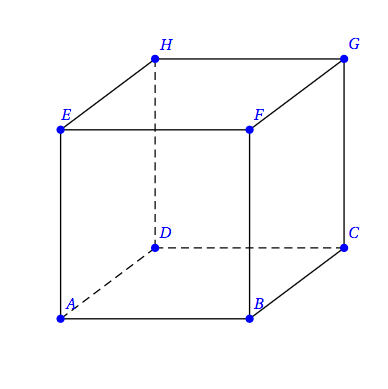
- Justifier qu'on peut inscrire ce tétraèdre dans un cube ABCDEFGH en positionnant deux atomes d'hydrogène sur les sommets A et C du cube et les deux autres atomes d'hydrogène sur deux autres sommets du cube. Représenter la molécule dans le cube donné en annexe page Annexe .
- Démontrer que l'atome de carbone est au centre $\Omega$ du cube.
- Déterminer l'arrondi au dixième de degré de la mesure de l'angle que forment entre elles les liaisons carbone-hydrogène, c'est-à-dire l'angle $\widehat{A\Omega C}$.
Dans la suite de l'exercice, on pourra travailler dans le repère $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.
Annexe ( A rendre avec la copie )
Correction de l'exercice 3 (4 points)
Les interactions électriques conduisent à modéliser la molécule de méthane CH$_4$ de la façon suivante :
- Les noyaux d'atomes d'hydrogène occupent les positions des quatre sommets d'un tétraèdre régulier.
- Le noyau de carbone au centre de la molécule est à égale distance des quatre atomes d'hydrogène.
L'objectif est de déterminer une mesure de l'angle entre deux liaisons carbone--hydrogène. Un tétraèdre régulier est un polyèdre dont les quatre faces sont des triangles équilatéraux.
- Justifier qu'on peut inscrire ce tétraèdre dans un cube ABCDEFGH en positionnant deux atomes d'hydrogène sur les sommets A et C du cube et les deux autres atomes d'hydrogène sur deux autres sommets du cube. Représenter la molécule dans le cube donné en annexe page Annexe .
- Démontrer que l'atome de carbone est au centre $\Omega$ du cube.
- Déterminer l'arrondi au dixième de degré de la mesure de l'angle que forment entre elles les liaisons carbone-hydrogène, c'est-à-dire l'angle $\widehat{A\Omega C}$.
Dans la suite de l'exercice, on pourra travailler dans le repère $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.
Annexe ( A rendre avec la copie )

Exercice 4 5 points
On s'intéresse à la chute d'une goutte d'eau qui se détache d'un nuage sans vitesse initiale. Un modèle très simplifié permet d'établir que la vitesse instantanée verticale, exprimée en m.s$^{-1}$, de chute de la goutte en fonction de la durée de chute $t$ est donnée par la fonction $v$ définie ainsi :
Pour tout réel positif ou nul $t$, $v(t) = 9,81\dfrac{m}{k}\left(1-\mathrm{e}^{-\frac{k}{m}t}\right)$ ; la constante $m$ est la masse de la goutte en milligramme et la constante $k$ est un coefficient strictement positif lié au frottement de l'air.
On rappelle que la vitesse instantanée est la dérivée de la position. Les partiesA et B sont indépendantes.
Partie A - Cas général
- Déterminer les variations de la vitesse de la goutte d'eau.
- La goutte ralentit -elle au cours de sa chute ?
- Montrer que $\lim\limits_{t\rightarrow +\infty}v(t)=9,81\dfrac{m}{k}$. Cette limite s'appelle vitesse limite de la goutte.
- Un scientifique affirme qu'au bout d'une durée de chute égale à $\dfrac{5m}{k}$, la vitesse de la goutte dépasse 99 % de sa vitesse limite. Cette affirmation est-elle correcte ?
Partie B
Dans cette partie, on prend $m = 6$ et $k = 3,9$. À un instant donné, la vitesse instantanée de cette goutte est 15 m.s$^{-l}.$
- Depuis combien de temps la goutte s'est-elle détachée de son nuage ? Arrondir la réponse au dixième de seconde.
- En déduire la vitesse moyenne de cette goutte entre le moment où elle s'est détachée du nuage et l'instant où on a mesuré sa vitesse. Arrondir la réponse au dixième de m.s$^{-1}$.
Correction de l'exercice 4 5 points
On s'intéresse à la chute d'une goutte d'eau qui se détache d'un nuage sans vitesse initiale. Un modèle très simplifié permet d'établir que la vitesse instantanée verticale, exprimée en m.s$^{-1}$, de chute de la goutte en fonction de la durée de chute $t$ est donnée par la fonction $v$ définie ainsi :
Pour tout réel positif ou nul $t$, $v(t) = 9,81\dfrac{m}{k}\left(1-\mathrm{e}^{-\frac{k}{m}t}\right)$ ; la constante $m$ est la masse de la goutte en milligramme et la constante $k$ est un coefficient strictement positif lié au frottement de l'air.
On rappelle que la vitesse instantanée est la dérivée de la position. Les partiesA et B sont indépendantes.
Partie A - Cas général
- Déterminer les variations de la vitesse de la goutte d'eau.
- La goutte ralentit -elle au cours de sa chute ?
- Montrer que $\lim\limits_{t\rightarrow +\infty}v(t)=9,81\dfrac{m}{k}$. Cette limite s'appelle vitesse limite de la goutte.
- Un scientifique affirme qu'au bout d'une durée de chute égale à $\dfrac{5m}{k}$, la vitesse de la goutte dépasse 99 % de sa vitesse limite. Cette affirmation est-elle correcte ?
Partie B
Dans cette partie, on prend $m = 6$ et $k = 3,9$. À un instant donné, la vitesse instantanée de cette goutte est 15 m.s$^{-l}.$
- Depuis combien de temps la goutte s'est-elle détachée de son nuage ? Arrondir la réponse au dixième de seconde.
- En déduire la vitesse moyenne de cette goutte entre le moment où elle s'est détachée du nuage et l'instant où on a mesuré sa vitesse. Arrondir la réponse au dixième de m.s$^{-1}$.
Spécialité 5 points
Une personne a mis au point le procédé de cryptage suivant :
- À chaque lettre de l'alphabet, on associe un entier $n$ comme indiqué ci-dessous : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline A &B &C &D &E &F &G &H &I &J&K &L &M\\\hline 0 &1 &2&3&4&5&6&7&8&9&10&11&12\\\hline\hline N &O &P&Q&R&S&T&U&V&W&X&Y&Z\\\hline 13&14 &15&16&17&18&19&20&21&22&23&24&25\\\hline \end{array}$$
- On choisit deux entiers $a$ et $b$ compris entre $0$ et $25$.
- Tout nombre entier $n$ compris entre 0 et 25 est codé par le reste de la division euclidienne de $an+ b$ par 26.
Le tableau suivant donne les fréquences $f$ en pourcentage des lettres utilisées dans un texte écrit en français. $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline Lettre&A &B &C &D &E &F &G &H &I &J&K &L &M\\\hline Fréquence&9,42&1,02&2,64&3,38&15,87&0,94&1,04&0,77&8?41&0,89&0,00&5,33&3,23\\\hline\hline Lettre&N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\\hline Fréquence&7,14&5,13&2,86&1,06&6,46&7,90&7,26&6,24&2,15&0,00&0,30&0,24&0,32\\\hline \end{array}$$
Partie A
Un texte écrit en français et suffisamment long a été codé selon ce procédé. L'analyse fréquentielle du texte codé a montré qu'il contient 15,9 % de O et 9,4 % de E. On souhaite déterminer les nombres $a$ et $b$ qui ont permis le codage.
- Quelles lettres ont été codées par les lettres O et E ?
- Montrer que les entiers $a$ et $b$ sont solutions du système \[\begin{cases}4a + b\equiv 14 [26] \\b \equiv 4 [26]. \end{cases}\]
- Déterminer tous les couples d'entiers $(a , b)$ ayant pu permettre le codage de ce texte.
Partie B
- On choisit $a = 22$ et $b = 4$.
- Coder les lettres K et X.
- Ce codage est-il envisageable ?
- On choisit $a = 9$ et $b = 4$.
- Montrer que pour tous entiers naturels $n$ et $m$, on a : \[m \equiv 9 n + 4 [26]\iff n\equiv 3 m + 14 [26] \]
- Décoder le mot AQ.
Correction de l'exercice de Spécialité 5 points
Une personne a mis au point le procédé de cryptage suivant :
- À chaque lettre de l'alphabet, on associe un entier $n$ comme indiqué ci-dessous : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline A &B &C &D &E &F &G &H &I &J&K &L &M\\\hline 0 &1 &2&3&4&5&6&7&8&9&10&11&12\\\hline\hline N &O &P&Q&R&S&T&U&V&W&X&Y&Z\\\hline 13&14 &15&16&17&18&19&20&21&22&23&24&25\\\hline \end{array}$$
- On choisit deux entiers $a$ et $b$ compris entre $0$ et $25$.
- Tout nombre entier $n$ compris entre 0 et 25 est codé par le reste de la division euclidienne de $an+ b$ par 26.
Le tableau suivant donne les fréquences $f$ en pourcentage des lettres utilisées dans un texte écrit en français. $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline Lettre&A &B &C &D &E &F &G &H &I &J&K &L &M\\\hline Fréquence&9,42&1,02&2,64&3,38&15,87&0,94&1,04&0,77&8?41&0,89&0,00&5,33&3,23\\\hline\hline Lettre&N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\\hline Fréquence&7,14&5,13&2,86&1,06&6,46&7,90&7,26&6,24&2,15&0,00&0,30&0,24&0,32\\\hline \end{array}$$
Partie A
Un texte écrit en français et suffisamment long a été codé selon ce procédé. L'analyse fréquentielle du texte codé a montré qu'il contient 15,9 % de O et 9,4 % de E. On souhaite déterminer les nombres $a$ et $b$ qui ont permis le codage.
- Quelles lettres ont été codées par les lettres O et E ?
- Montrer que les entiers $a$ et $b$ sont solutions du système \[\begin{cases}4a + b\equiv 14 [26] \\b \equiv 4 [26]. \end{cases}\]
- Déterminer tous les couples d'entiers $(a , b)$ ayant pu permettre le codage de ce texte.
Partie B
- On choisit $a = 22$ et $b = 4$.
- Coder les lettres K et X.
- Ce codage est-il envisageable ?
- On choisit $a = 9$ et $b = 4$.
- Montrer que pour tous entiers naturels $n$ et $m$, on a : \[m \equiv 9 n + 4 [26]\iff n\equiv 3 m + 14 [26] \]
- Décoder le mot AQ.
- Vues: 32908
