Baccalauréat S Amérique du Sud 21 novembre 2017
Exercice 1 6 points
La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d'eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins $80$ avec $1$ litre de pâte liquide au chocolat. 
Partie A : modélisation par une fonction
Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = \dfrac{x^2 - 2x - 2 - 3\ln x}{x}.\] La représentation graphique de la fonction $f$ est donnée ci-dessous. 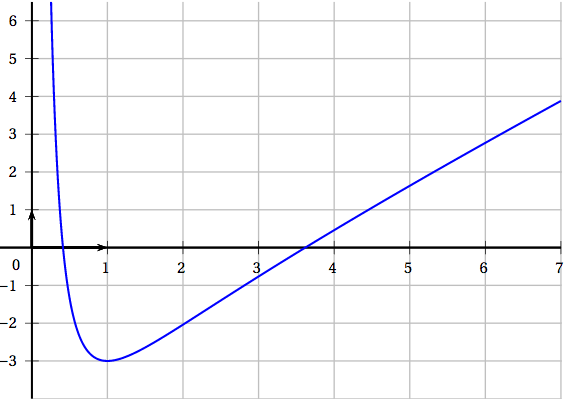
Le repère est orthogonal d'unité $2$ cm en abscisses et $1$ cm en ordonnées.
- Soit $\varphi$ la fonction définie sur $]0~;~+ \infty[$ par : \[\varphi(x) = x^2 - 1 + 3\ln x.\]
- Calculer $\varphi(1)$ et la limite de $\varphi$ en $0$.
- Étudier les variations de $\varphi$ sur $]0~;~+ \infty[$. En déduire le signe de $\varphi(x)$ selon les valeurs de $x$.
-
- Calculer les limites de $f$ aux bornes de son ensemble de définition.
- Montrer que sur $]0~;~+ \infty[$ : $f'(x) = \dfrac{\varphi(x)}{x^2}$. En déduire le tableau de variation de $f$.
- Prouver que l'équation $f(x) = 0$ admet une unique solution $\alpha$ sur $]0~;~1]$. Déterminer à la calculatrice une valeur approchée de $\alpha$ à $10^{-2}$ près. On admettra que l'équation $f(x) = 0$ a également une unique solution $\beta$ sur $[1~;~+ \infty[$ avec $\beta \approx 3,61$ à $10^{-2}$ près.
- Soit $F$ la fonction définie sur $]0~;~+ \infty[$ par : \[F(x) = \dfrac{1}{2}x^2 - 2x - 2\ln x - \dfrac{3}{2}(\ln x)^2.\] Montrer que $F$ est une primitive de $f$ sur $]0~;~+ \infty[$.
Partie B : résolution du problème
Dans cette partie, les calculs seront effectués avec les valeurs approchées à $10^{-2}$ près de $\alpha$ et $\beta$ de la partie .
Pour obtenir la forme de la goutte, on considère la courbe représentative $C$ de la fonction $f$ restreinte à l'intervalle $[\alpha~;~\beta]$ ainsi que son symétrique $C'$ par rapport à l'axe des abscisses. Les deux courbes $C$ et $C'$ délimitent la face supérieure du palet. Pour des raisons esthétiques, le chocolatier aimerait que ses palets aient une épaisseur de $0,5$ cm. Dans ces conditions, la contrainte de rentabilité serait-elle respectée ?
Correction de l'exercice 1 (5 points)
La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d'eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins $80$ avec $1$ litre de pâte liquide au chocolat. 
Partie A : modélisation par une fonction
Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = \dfrac{x^2 - 2x - 2 - 3\ln x}{x}.\] La représentation graphique de la fonction $f$ est donnée ci-dessous. 
Le repère est orthogonal d'unité $2$ cm en abscisses et $1$ cm en ordonnées.
- Soit $\varphi$ la fonction définie sur $]0~;~+ \infty[$ par : \[\varphi(x) = x^2 - 1 + 3\ln x.\]
- Calculer $\varphi(1)$ et la limite de $\varphi$ en $0$. $\varphi(1)=1^2-1+3\ln(1)=0$
- Étudier les variations de $\varphi$ sur $]0~;~+ \infty[$. En déduire le signe de $\varphi(x)$ selon les valeurs de $x$. La fonction $\varphi$ est dérivable sur $]0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
$\lim\limits_{x \to 0^+}x^2-1=-1$ et $\lim\limits_{x \to 0^+} \ln(x)=-\infty$
Donc $\lim\limits_{x \to 0^+}\varphi(x)=-\infty$
$\quad$
$\varphi'(x)=2x+\dfrac{3}{x} >0$ sur $]0;+\infty[$.
La fonction $\varphi$ est donc strictement croissante sur $]0;+\infty[$.
$\quad$
Puisque $\varphi(1)=0$ cela signifie donc que :
– $\varphi(x)<0$ sur l’intervalle $]0;1[$
– $\varphi(1)=0$
– $\varphi(x)>0$ sur l’intervalle $]1;+\infty[$
$\quad$ -
- Calculer les limites de $f$ aux bornes de son ensemble de définition. $f(x)=\dfrac{x^2-2x-2-3\ln(x)}{x}$
- Montrer que sur $]0~;~+ \infty[$ : $f'(x) = \dfrac{\varphi(x)}{x^2}$. En déduire le tableau de variation de $f$. La fonction $f$ est dérivable sur l’intervalle $]0;+\infty[$ en tant que somme et quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
- Signe de la dérivée :

- Tableau de variations :
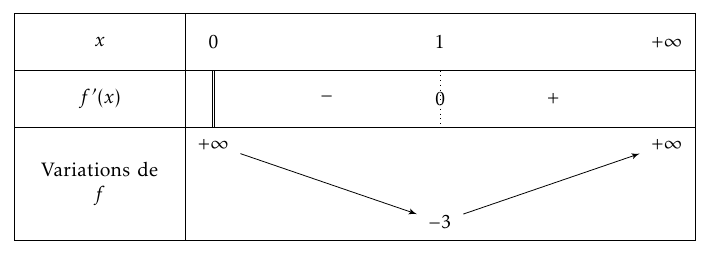
- Prouver que l'équation $f(x) = 0$ admet une unique solution $\alpha$ sur $]0~;~1]$. Déterminer à la calculatrice une valeur approchée de $\alpha$ à $10^{-2}$ près. On admettra que l'équation $f(x) = 0$ a également une unique solution $\beta$ sur $[1~;~+ \infty[$ avec $\beta \approx 3,61$ à $10^{-2}$ près. La fonction $f$ est continue (car dérivable) et strictement décroissante sur l’intervalle $]0;1]$.
- Soit $F$ la fonction définie sur $]0~;~+ \infty[$ par : \[F(x) = \dfrac{1}{2}x^2 - 2x - 2\ln x - \dfrac{3}{2}(\ln x)^2.\] Montrer que $F$ est une primitive de $f$ sur $]0~;~+ \infty[$. $F$ est dérivable sur l’intervalle $]0;+\infty[$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
$\lim\limits_{x \to 0^+}x^2-2x-2=-2$ et $\lim\limits_{x \to 0^+} -3\ln(x)=+\infty$
Donc $\lim\limits_{x \to 0^+} x^2-2x-2-3\ln(x)=+\infty$
$\lim\limits_{x \to 0^+} \dfrac{1}{x}=+\infty$
Par conséquent $\lim\limits_{x \to 0^+} f(x)=+\infty$
$\quad$
$f(x)=x-2-\dfrac{2}{x}-3\dfrac{\ln(x)}{x}$
$\lim\limits_{x \to +\infty}x-2=+\infty$, $\lim\limits_{x \to +\infty} \dfrac{2}{x}=0$ et $\lim\limits_{x \to +\infty} \dfrac{\ln(x)}{x}=0$
Donc $\lim\limits_{x \to +\infty} f(x)=+\infty$
$\quad$
$\begin{align*} f'(x)&=\dfrac{\left(2x-2-\dfrac{3}{x}\right)x-\left(x^2-2x-2-3\ln(x)\right)}{x^2} \\
&=\dfrac{2x^2-2x-3-x^2+2x+2+3\ln(x)}{x^2}\\
&=\dfrac{x^2-1+3\ln(x)}{x^2}\\
&=\dfrac{\varphi(x)}{x^2}
\end{align*}$
$\quad$
$\lim\limits_{x \to 0^+} f(x)=+\infty$ et $f(1)=-3$
Donc $0\in[-3;+\infty[$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=0$ possède une unique solution $\alpha$ sur l’intervalle $]0;1]$.
À l’aide de la calculatrice on trouve $\alpha\approx 0,41$
$\quad$
$\begin{align*} F'(x)&=\dfrac{1}{2}\times 2x-2-\dfrac{2}{x}-\dfrac{3}{2}\times 2\times \dfrac{1}{x}\times \ln(x) \\
&=x-2-\dfrac{2}{x}-\dfrac{3\ln(x)}{x} \\
&=\dfrac{x^2-2x-2-3\ln(x)}{x}\\
&=f(x)
\end{align*}$
La fonction $F$ est donc une primitive de la fonction $f$ sur l’intervalle $]0;1[$.
$\quad$
Partie B : résolution du problème
Dans cette partie, les calculs seront effectués avec les valeurs approchées à $10^{-2}$ près de $\alpha$ et $\beta$ de la partie .
La fonction $-f$ est positive sur l’intervalle $[\alpha;\beta]$.
Calculons l’aire $I$ du domaine compris entre la courbe $C’$, l’axe des abscisses et les droites d’équation $x=\alpha$ et $x=\beta$.
$\begin{align*} I&=\displaystyle \int_{\alpha}^{\beta} -f(x)\;dx \\
&=-\left(F(\beta)-F(\alpha)\right) \\
&\approx 5,598
\end{align*}$
L’aire $\mathscr{A}$ de la face supérieure est donc $2I\approx 11,196$ u.a.
Or $1$u.a. = 2 cm$^2$
Donc $\mathscr{A}\approx 22,392$ cm$^2$.
Le volume du palet est $V=\mathscr{A} \times 0,5\approx 11,196$ cm$^2$.
Par conséquent $80$ palets ont un volume de $80V\approx 895,68$ cm$^3$ (qui est bien inférieur à $1$ litre $=1~000$ cm$^3$) .
La contrainte de rentabilité est donc respectée.
$\quad$
Exercice 2 (4 points)
On considère un cube ABCDEFGH.
-
- Simplifier le vecteur $\vec{\text{AC}} + \vec{\text{AE}}$.
- En déduire que $\vec{\text{AG}}~\cdot~\vec{\text{BD}} = 0$.
- On admet que $\vec{\text{AG}}~\cdot~\vec{\text{BE}} = 0$. Démontrer que la droite (AG) est orthogonale au plan (BDE).
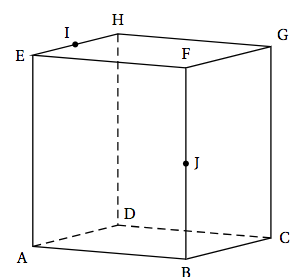
- L'espace est muni du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Démontrer qu'une équation cartésienne du plan (BDE) est $x + y + z - 1 = 0$.
- Déterminer les coordonnées du point d'intersection K de la droite (AG) et du plan (BDE).
- On admet que l'aire, en unité d'aire, du triangle BDE est égale à $\dfrac{\sqrt{3}}{2}$. Calculer le volume de la pyramide BDEG.
Correction de l'exercice 2 (4 points)
On considère un cube ABCDEFGH.
-
- Simplifier le vecteur $\vec{\text{AC}} + \vec{\text{AE}}$. $\vec{AC}+\vec{AE}=\vec{AC}+\vec{CG}=\vec{AG}$ d’après la relation de Chasles.
- En déduire que $\vec{\text{AG}}~\cdot~\vec{\text{BD}} = 0$. $\begin{align*} \vec{AG}.\vec{BD}&=\left(\vec{AC}+\vec{AE}\right).\vec{BD} \\
- On admet que $\vec{\text{AG}}~\cdot~\vec{\text{BE}} = 0$. Démontrer que la droite (AG) est orthogonale au plan (BDE). Le vecteur $\vec{AG}$ est othogonal à deux vecteurs non colinéaires du plan $(BDE)$. Il est donc orthogonal à ce plan.
$\quad$
&=\vec{AC}.\vec{BD}+\vec{AE}.\vec{BD} \\
&=0+0\\
&=0
\end{align*}$
$\vec{AC}.\vec{BD}=0$ car $[AC]$ et $[BD]$ sont les diagonales du carré $BCD$ (donc perpendiculaires entre-elles).
$\vec{AE}.\vec{BD}=0$ car $(AE)$ est orthogonale au plan $BCD$
$\quad$
Par conséquent la droite $(AG)$ est orthogonale au plan $(BDE)$.
- L'espace est muni du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Démontrer qu'une équation cartésienne du plan (BDE) est $x + y + z - 1 = 0$. Dans le repère $\left(A;\vec{AB},\vec{AD},\vec{AE}\right)$ on a $A(0;0;0)$ et $G(1;1;1)$.
- Déterminer les coordonnées du point d'intersection K de la droite (AG) et du plan (BDE). Une représentation paramétrique de la droite $(AG)$ est $\begin{cases} x=k\\y=k\\z=k\end{cases}$ $\quad k\in \mathbb{R}$.
- On admet que l'aire, en unité d'aire, du triangle BDE est égale à $\dfrac{\sqrt{3}}{2}$. Calculer le volume de la pyramide BDEG. On a $KG=\sqrt{\left(1-\dfrac{1}{3}\right)^2+\left(1-\dfrac{1}{3}\right)^2+\left(1-\dfrac{1}{3}\right)^2}=\sqrt{\dfrac{12}{9}}=\dfrac{2\sqrt{3}}{3}$.
Par conséquent $\vec{AG}(1;1;1)$.
Une équation cartésienne du plan $(BDE)$ est donc de la forme $x+y+z+d=0$.
Le point $B(1;0;0)$ appartient à ce plan donc $1+0+0+d=0 \iff d=-1$.
Une équation cartésienne du plan $(BDE)$ est donc $x+y+z+z-1=0$.
$\quad$
Le point $K$ appartient à la fois à la droite $(AG)$ et au plan $(BDE)$.
Ses coordonnées sont donc solution du système :
$\begin{align*} \begin{cases} x=k\\y=k\\z=k\\x+y+z-1=0\end{cases} & \iff \begin{cases} x=k\\y=k\\z=k\\3k-1=0\end{cases} \\
&\iff \begin{cases} x=k\\y=k\\z=k\\k=\dfrac{1}{3}\end{cases}\\
&\iff \begin{cases} x=\dfrac{1}{3}\\y=\dfrac{1}{3}\\z=\dfrac{1}{3}\\k=\dfrac{1}{3}\end{cases}
\end{align*}$.
Donc $K\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3}\right)$.
$\quad$
Le volume de la pyramide $BDEG$ est :
$\begin{align*} V&=\dfrac{\text{aire}_{BDE}\times KG}{3}\\
&=\dfrac{\dfrac{\sqrt{3}}{2}\times \dfrac{2\sqrt{3}}{3}}{3} \\
&=\dfrac{1}{3}
\end{align*}$
$\quad$
Exercice 3 (3 points)
Partie A
Un organisme de contrôle sanitaire s'intéresse au nombre de bactéries d'un certain type contenues dans la crème fraîche. Pour cela, il effectue des analyses portant sur 10000 prélèvements de 1 ml de crème fraîche dans l'ensemble de la production française. Les résultats sont donnés dans le tableau et représentés dans l'histogramme ci-dessous : $$ \begin{array} {|c|c|c|c|c|c|c|}\hline \small \text{Nombre de bactéries (en milliers)}&[100~;~120[&[120~;~130[ &[130~;~140[&[140~;~150[ &[150~;~160[ &[160~;~180[\\ \hline \small \text{Nombre de prélèvements }& 1597 & 1284 & 2255 & 1808 & 1345 & 1711 \\ \hline \end{array} $$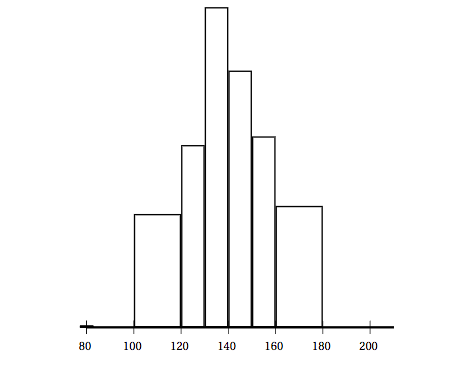
À l'aide de la calculatrice, donner une estimation de la moyenne et de l'écart-type du nombre de bactéries par prélèvement.
Partie B
L'organisme décide alors de modéliser le nombre de bactéries étudiées (en milliers par ml) présentes dans la crème fraîche par une variable aléatoire $X$ suivant la loi normale de paramètres $\mu = 140$ et $\sigma = 19$.
-
- Ce choix de modélisation est-il pertinent? Argumenter.
- On note $p = P(X \geqslant 160)$. Déterminer la valeur arrondie de $p$ à $10^{-3}$.
- Lors de l'inspection d'une laiterie, l'organisme de contrôle sanitaire analyse un échantillon de $50$ prélèvements de $1$ ml de crème fraîche dans la production de cette laiterie ; $13$ prélèvements contiennent plus de $160$ milliers de bactéries.
- L'organisme déclare qu'il y a une anomalie dans la production et qu'il peut l'affirmer en ayant une probabilité de 0,05 de se tromper. Justifier sa déclaration.
- Aurait-il pu l'affirmer avec une probabilité de $0,01$ de se tromper ?
Correction de l'exercice 3 (3 points)
Partie A
Un organisme de contrôle sanitaire s'intéresse au nombre de bactéries d'un certain type contenues dans la crème fraîche. Pour cela, il effectue des analyses portant sur 10000 prélèvements de 1 ml de crème fraîche dans l'ensemble de la production française. Les résultats sont donnés dans le tableau et représentés dans l'histogramme ci-dessous : $$ \begin{array} {|c|c|c|c|c|c|c|}\hline \small \text{Nombre de bactéries (en milliers)}&[100~;~120[&[120~;~130[ &[130~;~140[&[140~;~150[ &[150~;~160[ &[160~;~180[\\ \hline \small \text{Nombre de prélèvements }& 1597 & 1284 & 2255 & 1808 & 1345 & 1711 \\ \hline \end{array} $$
On va utiliser le centre de chacune des classes et utiliser le tableau suivant pour calculer, à l’aide de la calculatrice, les valeurs demandées.
$\begin{array}{|l|c|c|c|c|c|c|}
\hline
\text{Centre}&110&125&135&145&155&170\\
\hline
\text{Effectif}&1~597&1~284&2~255&1~808&1~345&1~711\\
\hline
\end{array}$
Une estimation de la moyenne est $\overline{x}=140,21$ et une estimation de l’écart-type est $\sigma\approx 19,16$.
$\quad$
Partie B
L'organisme décide alors de modéliser le nombre de bactéries étudiées (en milliers par ml) présentes dans la crème fraîche par une variable aléatoire $X$ suivant la loi normale de paramètres $\mu = 140$ et $\sigma = 19$.
-
- Ce choix de modélisation est-il pertinent? Argumenter. Le nombre de bactéries présentes dépend de plusieurs facteurs : températures, hygiène, soucis sur la chaîne de production, … Une loi normale est donc bien appropriée pour modéliser la situation étudiée.
- On note $p = P(X \geqslant 160)$. Déterminer la valeur arrondie de $p$ à $10^{-3}$. $p=P(X\geqslant 160)=0,5-P(140 \leqslant X \leqslant160) \approx 0,146$
À la partie A, nous avons obtenu des estimations de moyenne et d’écart-type très proche des valeurs proposées.
Le choix de modélisation proposé est donc pertinent.
$\quad$
$\quad$ ou de façon plus directe :2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$ - Lors de l'inspection d'une laiterie, l'organisme de contrôle sanitaire analyse un échantillon de $50$ prélèvements de $1$ ml de crème fraîche dans la production de cette laiterie ; $13$ prélèvements contiennent plus de $160$ milliers de bactéries.
- L'organisme déclare qu'il y a une anomalie dans la production et qu'il peut l'affirmer en ayant une probabilité de 0,05 de se tromper. Justifier sa déclaration. On a $n=50 \geq 30$ et $p=0,146$ donc $np=7,3\geq 5$ et $n(1-p)=42,7\geq 5$
- Aurait-il pu l'affirmer avec une probabilité de $0,01$ de se tromper ? Un intervalle de fluctuation asymptotique au seuil de $99\%$ est
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est
$\begin{align*} I_{50}&=\left[0,146-1,96\sqrt{\dfrac{0,146\times 0,854}{50}};0,146+1,96\sqrt{\dfrac{0,146\times 0,854}{50}}\right] \\
&\approx [0,048;0,244]
\end{align*}$
La fréquence observée est $f=\dfrac{13}{50}=0,26\notin I_{50}$
On peut donc affirmer au risque de $5\%$ qu’il y a une anomalie dans la production.
$\quad$
$\begin{align*} J_{50}&=\left[0,146-2,58\sqrt{\dfrac{0,146\times 0,854}{50}};0,146+2,58\sqrt{\dfrac{0,146\times 0,854}{50}}\right] \\
&\approx [0,017;0,275]
\end{align*}$
La fréquence observée $f$ appartient alors à l’intervalle $J_{50}$.
Au risque de $1\%$, on ne peut donc pas affirmer qu’il y a une anomalie dans la production.
$\quad$
Exercice 4 3 points
Dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$, on considère les points A et B d'affixes respectives $z_{\text{A}} = 2\text{e}^{\text{i}\frac{\pi}{4}}$ et $z_{\text{B}} = 2\text{e}^{\text{i}\frac{3\pi}{4}}$ 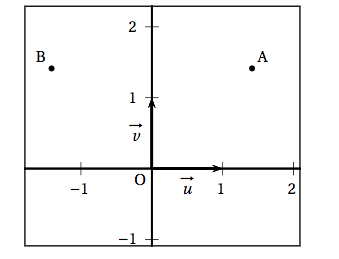
- Montrer que OAB est un triangle rectangle isocèle.
- On considère l'équation \[(E) \::\: z^2 - \sqrt{6}\,z + 2 = 0.\] Montrer qu'une des solutions de $(E)$ est l'affixe d'un point situé sur le cercle circonscrit au triangle OAB.
Correction de l'exercice 4 3 points
Dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$, on considère les points A et B d'affixes respectives $z_{\text{A}} = 2\text{e}^{\text{i}\frac{\pi}{4}}$ et $z_{\text{B}} = 2\text{e}^{\text{i}\frac{3\pi}{4}}$ 
- Montrer que OAB est un triangle rectangle isocèle. $\dfrac{z_B-z_O}{z_A-z_O}=\dfrac{2\text{e}^{\text{i} \pi/4}}{2\text{e}^{3\text{i} \pi/4}}=\text{e}^{\text{i} \pi/2}$.
- On considère l'équation \[(E) \::\: z^2 - \sqrt{6}\,z + 2 = 0.\] Montrer qu'une des solutions de $(E)$ est l'affixe d'un point situé sur le cercle circonscrit au triangle OAB. Le centre $I$ du cercle circonscrit au triangle $OAB$ est le milieu de l’hypoténuse $[AB]$.
Par conséquent $\left(\vec{OA};\vec{OB}\right)=$arg$\left(\dfrac{z_B-z_O}{z_A-z_O}\right)=\dfrac{\pi}{2}+2k\pi$ avec $k\in \mathbb{Z}$.
De plus $\left|\dfrac{z_B-z_O}{z_A-z_O}\right|=1$.
Le triangle $OAB$ est donc rectangle isocèle en $O$.
$\quad$
Par conséquent
$\begin{align*}z_I&=\dfrac{z_A+z_B}{2}\\
&=\dfrac{2\left(\cos \dfrac{\pi}{4}+\text{i} \sin \dfrac{\pi}{4}\right)+2\left(\cos \dfrac{3\pi}{4}+\text{i} \sin \dfrac{3\pi}{4}\right)}{2}\\
&=\dfrac{\sqrt{2}}{2}+\text{i} \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}+\text{i} \dfrac{\sqrt{2}}{2}\\
&=\text{i}\sqrt{2}
\end{align*}$
$OA=\left|z_A\right|=2$.
On applique le théorème de Pythagore dans le triangle $OAB$ : $AB^2=OA^2+OB^2=8$.
Donc $AB=2\sqrt{2}$.
Le rayon du cercle circonscrit au cercle $OAB$ est donc $R=\dfrac{AB}{2}=\sqrt{2}$.
On considère l’équation $(E)~~ :~~ z^2-\sqrt{6}z+2=0$
$\Delta=6-8=-2<0$
Il y a donc deux solutions complexes :
$z_1=\dfrac{\sqrt{6}-\text{i}\sqrt{2}}{2}$ et $z_2=\overline{z_1}=\dfrac{\sqrt{6}+\text{i}\sqrt{2}}{2}$
$\begin{align*} \left|z_2-z_I\right|&=\left|\dfrac{\sqrt{6}+\text{i}\sqrt{2}}{2}-\text{i}\sqrt{2}\right| \\
&=\left|\dfrac{\sqrt{6}-\text{i}\sqrt{2}}{2}\right|\\
&=\sqrt{\dfrac{6+2}{4}}\\
&=\sqrt{2}\\
&=R
\end{align*}$
Ainsi le point d’affixe $z_2$ appartient au cercle circonscrit au triangle $OAB$.
$\quad$
Exercice 5 (5 points)
Un biologiste souhaite étudier l'évolution de la population d'une espèce animale dans une réserve. Cette population est estimée à 12000 individus en 2016. Les contraintes du milieu naturel font que la population ne peut pas dépasser les 60000 individus.
Partie A : un premier modèle
Dans une première approche, le biologiste estime que la population croît de 5 % par an. L'évolution annuelle de la population est ainsi modélisée par une suite $\left(v_n\right)$ où $v_n$ représente le nombre d'individus, exprimé en milliers, en $2016 + n$. On a donc $v_0 = 12$.
- Déterminer la nature de la suite $\left(v_n\right)$ et donner l'expression de $v_n$ en fonction de $n$.
- Ce modèle répond-il aux contraintes du milieu naturel ?
Partie B : un second modèle
Le biologiste modélise ensuite l'évolution annuelle de la population par une suite $\left(u_n\right)$ définie par $u_0 = 12$ et, pour tout entier naturel $n$, $u_{n+1} = - \dfrac{1,1}{605} u_n^2 + 1,1 u_n$.
- On considère la fonction $g$ définie sur $\mathbb{R}$ par \[g(x) = - \dfrac{1,1}{605}x^2 + 1,1 x.\]
- Justifier que $g$ est croissante sur [0~;~60].
- Résoudre dans $\mathbb{R}$ l'équation $g(x) = x$.
- On remarquera que $u_{n+1} = g\left(u_n\right)$.
- Calculer la valeur arrondie à $10^{-3}$ de $u_1$. Interpréter.
- Démontrer par récurrence que, pour tout entier naturel $n$, $0 \leqslant u_n \leqslant 55$.
- Démontrer que la suite $\left(u_n\right)$ est croissante.
- En déduire la convergence de la suite $\left(u_n\right)$.
- On admet que la limite $\ell$ de la suite $\left(u_n\right)$ vérifie $g(\ell) = \ell$. En déduire sa valeur et l'interpréter dans le contexte de l'exercice.
- Le biologiste souhaite déterminer le nombre d'années au bout duquel la population dépassera les 50000 individus avec ce second modèle. Il utilise l'algorithme suivant. $$ \begin{array}{ |l|l|}\hline \text{Variables } & n \text{ un entier naturel}\\ &u \text{ un nombre réel}\\ \hline \text{Traitement} &n \text{ prend la valeur }0 \\ & u \text{ prend la valeur } 12\\ &\text{Tant Que} \cdots\\ &\hspace{1.5cm} u \text{ prend la valeur } \cdots\\ &\hspace{1.5cm} n \text{ prend la valeur } \cdots\\ &\text{Fin Tant Que}\\ \hline \text{ Sortie } &\text{Afficher} \cdots\\ \hline \end{array} $$ Recopier et compléter cet algorithme afin qu'il affiche en sortie le plus petit entier $r$ tel que $u_r \geqslant 50$.
Exercice 5 (5 points)
Un biologiste souhaite étudier l'évolution de la population d'une espèce animale dans une réserve. Cette population est estimée à 12000 individus en 2016. Les contraintes du milieu naturel font que la population ne peut pas dépasser les 60000 individus.
Partie A : un premier modèle
Dans une première approche, le biologiste estime que la population croît de 5 % par an. L'évolution annuelle de la population est ainsi modélisée par une suite $\left(v_n\right)$ où $v_n$ représente le nombre d'individus, exprimé en milliers, en $2016 + n$. On a donc $v_0 = 12$.
- Déterminer la nature de la suite $\left(v_n\right)$ et donner l'expression de $v_n$ en fonction de $n$. Chaque année la population est multipliée par $1,05$.
- Ce modèle répond-il aux contraintes du milieu naturel ? $1,05>1$ donc $\lim\limits_{n\to +\infty} 1,05^n=+\infty$ et $\lim\limits_{n\to +\infty} v_n=+\infty$
La suite $\left(v_n\right)$ est donc géométrique de raison $1,05$ et de premier terme $v_0=12$.
Ainsi, pour tout entier naturel $n$, on a $v_n=12\times 1,05^n$.
$\quad$
Ce modèle ne répond donc pas aux contraintes du milieu naturel.
$\quad$
Partie B : un second modèle
Le biologiste modélise ensuite l'évolution annuelle de la population par une suite $\left(u_n\right)$ définie par $u_0 = 12$ et, pour tout entier naturel $n$, $u_{n+1} = - \dfrac{1,1}{605} u_n^2 + 1,1 u_n$.
- On considère la fonction $g$ définie sur $\mathbb{R}$ par \[g(x) = - \dfrac{1,1}{605}x^2 + 1,1 x.\]
- Justifier que $g$ est croissante sur [0~;~60]. La fonction $g$ est dérivable sur l’intervalle $[0;60]$ en tant que fonction polynôme.
- Résoudre dans $\mathbb{R}$ l'équation $g(x) = x$.
$g'(x)=-\dfrac{-2,2}{605}x+1,1$
Donc
$\begin{align*} g'(x)>0 &\iff -\dfrac{-2,2}{605}x+1,1>0 \\
&\iff -\dfrac{2,2}{605}x > -1,1 \\
&\iff x<302,5
\end{align*}$
La fonction $g$ est donc croissante sur l’intervalle $[0;60]$.
$\begin{align*} g(x)=x &\iff -\dfrac{1,1}{605}x^2+1,1x=x \\
&\iff -\dfrac{1,1}{605}x^2+0,1x=0 \\
&\iff x\left(-\dfrac{1,1}{605}x+0,1\right)=0 \\
&\iff x=0 \text{ ou } -\dfrac{1,1}{605}x+0,1=0\\
&\iff x=0 \text{ ou } x= 55
\end{align*}$
L’équation $g(x)=x$ possède donc deux solutions dans $\mathbb{R}$ qui sont $0$ et $55$.
$\quad$ - On remarquera que $u_{n+1} = g\left(u_n\right)$.
- Calculer la valeur arrondie à $10^{-3}$ de $u_1$. Interpréter. $u_1=g(12)\approx 12,938$.
- Démontrer par récurrence que, pour tout entier naturel $n$, $0 \leqslant u_n \leqslant 55$. Initialisation : Si $n=0$ alors $u_0=12$ donc $0 \leq u_0 \leq 55$.
- Démontrer que la suite $\left(u_n\right)$ est croissante. Initialisation : Si $n=0$ alors $u_0=12$ donc $0 \leq u_0 \leq 55$.
- En déduire la convergence de la suite $\left(u_n\right)$. La suite $\left(u_n\right)$ est croissante et majorée par $55$: elle est donc convergente.
- On admet que la limite $\ell$ de la suite $\left(u_n\right)$ vérifie $g(\ell) = \ell$. En déduire sa valeur et l'interpréter dans le contexte de l'exercice. D’après la question B.1.b. les solutions de l’équation $g(\ell)=\ell$ sont $0$ et $55$.
Cela signifie donc qu’en 2017 la population de l’espèce sera environ de $12~938$ individus.
$\quad$
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $0 \leq u_n \leq 55$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $0 \leq u_{n+1} \leq 55$.
La fonction $g$ est croissante sur l’intervalle $[0;60]$
Puisque $u_{n+1}=g\left(u_n\right)$
Cela signifie que $g(0) \leq u_{n+1} \leq g(55) \iff 0 \leq u_{n+1} \leq 55$.
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $0 \leq u_n \leq 55$
$\quad$
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $0 \leq u_n \leq 55$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $0 \leq u_{n+1} \leq 55$.
La fonction $g$ est croissante sur l’intervalle $[0;60]$
Puisque $u_{n+1}=g\left(u_n\right)$
Cela signifie que $g(0) \leq u_{n+1} \leq g(55) \iff 0 \leq u_{n+1} \leq 55$.
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $0 \leq u_n \leq 55$
$\quad$
$\quad$
La suite $\left(u_n\right)$ est croissante et $u_0=12$ donc $\ell=55$.
Par conséquent $\lim\limits_{n \to +\infty}u_n=55$.
Cela signifie que la population étudiée, au bout d’un grand nombre d’années, sera de $55~000$ individus.
Les contraintes du milieu naturel sont donc respectées.
$\quad$ - Le biologiste souhaite déterminer le nombre d'années au bout duquel la population dépassera les 50000 individus avec ce second modèle. Il utilise l'algorithme suivant. $$ \begin{array}{ |l|l|}\hline \text{Variables } & n \text{ un entier naturel}\\ &u \text{ un nombre réel}\\ \hline \text{Traitement} &n \text{ prend la valeur }0 \\ & u \text{ prend la valeur } 12\\ &\text{Tant Que} \cdots\\ &\hspace{1.5cm} u \text{ prend la valeur } \cdots\\ &\hspace{1.5cm} n \text{ prend la valeur } \cdots\\ &\text{Fin Tant Que}\\ \hline \text{ Sortie } &\text{Afficher} \cdots\\ \hline \end{array} $$ Recopier et compléter cet algorithme afin qu'il affiche en sortie le plus petit entier $r$ tel que $u_r \geqslant 50$. Variables :
$\quad$ $n$ un entier naturel
$\quad$ $u$ un nombre réel
Traitement :
$\quad$ $n$ prend la valeur $0$
$\quad$ $u$ prend la valeur $12$
$\quad$ Tant Que $u< 50$
$\qquad$ $u$ prend la valeur $-\dfrac{1,1}{605}u^2+1,1u$
$\qquad$ $n$ prend la valeur $n+1$
$\quad$ Fin Tant Que
Sortie :
$\quad$ Afficher $n$
$\quad$
Spécialité 5 points
Dans un jeu vidéo en ligne, les joueurs peuvent décider de rejoindre l'équipe A (statut noté A) ou l'équipe B (statut noté B) ou bien de n'en rejoindre aucune et rester ainsi solitaire (statut noté S). Chaque jour, chaque joueur peut changer de statut mais ne peut pas se retirer du jeu. Les données recueillies sur les premières semaines après le lancement du jeu ont permis de dégager les tendances suivantes :
- un joueur de l'équipe A y reste le jour suivant avec une probabilité de $0,6$ ; il devient joueur solitaire avec une probabilité de $0,25$. Sinon, il rejoint l'équipe B ;
- un joueur de l'équipe B y reste le jour suivant avec une probabilité de $0,6$ ; sinon, il devient joueur solitaire avec une probabilité identique à celle de rejoindre l'équipe A ;
- un joueur solitaire garde ce statut le jour suivant avec une probabilité de $\dfrac{1}{7}$ ; il rejoint l'équipe B avec une probabilité 3 fois plus élevée que celle de rejoindre l'équipe A.
Au début du jeu, à la clôture des inscriptions, tous les joueurs sont solitaires. On note $U_n = \begin{pmatrix}a_n& b_n& s_n\end{pmatrix}$ l'état probabiliste des statuts d'un joueur au bout de $n$ jours. Ainsi $a_n$ est la probabilité d'être dans l'équipe A, $b_n$ celle d'être dans l'équipe B et $s_n$ celle d'être un joueur solitaire, après $n$ jours de jeu. On a donc : $a_0 = 0$, $b_0 = 0$ et $s_0 = 1$.
- On note $p$ la probabilité qu'un joueur solitaire un jour donné passe dans l'équipe A le jour suivant. Justifier que $p = \dfrac{3}{14}$.
-
- Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.
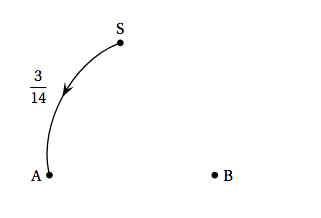
- On admet que la matrice de transition est $T = \begin{pmatrix} \frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\ \frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix}$. Pour tout entier naturel $n$, on a donc $U_{n+1} = U_n T$. Montrer alors que, pour tout entier naturel $n$, on a $U_n = U_0T^n$.
- Déterminer l'état probabiliste au bout d'une semaine, en arrondissant au millième.
- Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.
- On pose $V = \begin{pmatrix}300 &405 &182\end{pmatrix}$.
- Donner, sans détailler les calculs, le produit matriciel $VT$. Que constate-t-on ?
- En déduire un état probabiliste qui reste stable d'un jour sur l'autre.
- On donne l'algorithme suivant, où la commande « $U[i]$ » renvoie le coefficient de la $i$-ème colonne d'une matrice ligne $U$. $$ \begin{array}{ |l|l|}\hline \text{Variables } & k \text{un entier naturel}\\ & U \text{ une matrice de taille } 1 \times 3 \\ & T \text{ une matrice carrée d'ordre } 3\\ \hline \text{Traitement } & U \text{ prend la valeur }\begin{pmatrix}0 &0 &1\end{pmatrix} \\ & T \text{ prend la valeur }\begin{pmatrix}\frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\\frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix} \\ &\text{ Pour } k \text{allant de 1 à 7}\\ &\hspace{1cm} U \text{ prend la valeur } UT \\ &\text{Fin Pour}\\ \hline \text{ Sortie }&\text{Afficher }U[1] \\ \hline \end{array} $$
- Quelle est la valeur numérique arrondie au millième de la sortie de cet algorithme ? L'interpréter dans le contexte de l'exercice.
- Recopier et modifier cet algorithme pour qu'il affiche la fréquence de joueurs solitaires au bout de $13$ jours.
Correction de l'exercice de Spécialité 5 points
Dans un jeu vidéo en ligne, les joueurs peuvent décider de rejoindre l'équipe A (statut noté A) ou l'équipe B (statut noté B) ou bien de n'en rejoindre aucune et rester ainsi solitaire (statut noté S). Chaque jour, chaque joueur peut changer de statut mais ne peut pas se retirer du jeu. Les données recueillies sur les premières semaines après le lancement du jeu ont permis de dégager les tendances suivantes :
- un joueur de l'équipe A y reste le jour suivant avec une probabilité de $0,6$ ; il devient joueur solitaire avec une probabilité de $0,25$. Sinon, il rejoint l'équipe B ;
- un joueur de l'équipe B y reste le jour suivant avec une probabilité de $0,6$ ; sinon, il devient joueur solitaire avec une probabilité identique à celle de rejoindre l'équipe A ;
- un joueur solitaire garde ce statut le jour suivant avec une probabilité de $\dfrac{1}{7}$ ; il rejoint l'équipe B avec une probabilité 3 fois plus élevée que celle de rejoindre l'équipe A.
Au début du jeu, à la clôture des inscriptions, tous les joueurs sont solitaires. On note $U_n = \begin{pmatrix}a_n& b_n& s_n\end{pmatrix}$ l'état probabiliste des statuts d'un joueur au bout de $n$ jours. Ainsi $a_n$ est la probabilité d'être dans l'équipe A, $b_n$ celle d'être dans l'équipe B et $s_n$ celle d'être un joueur solitaire, après $n$ jours de jeu. On a donc : $a_0 = 0$, $b_0 = 0$ et $s_0 = 1$.
- On note $p$ la probabilité qu'un joueur solitaire un jour donné passe dans l'équipe A le jour suivant. Justifier que $p = \dfrac{3}{14}$. Un joueur solitaire garde ce statut le jour suivant avec une probabilité de $\dfrac{1}{7}$;il rejoint l’équipe B avec une probabilité $3$ fois plus élevée que celle de rejoindre l’équipe A.
-
- Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.

- On admet que la matrice de transition est $T = \begin{pmatrix} \frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\ \frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix}$. Pour tout entier naturel $n$, on a donc $U_{n+1} = U_n T$. Montrer alors que, pour tout entier naturel $n$, on a $U_n = U_0T^n$. Montrons par récurrence cette propriété.
- Déterminer l'état probabiliste au bout d'une semaine, en arrondissant au millième. On a $U_1=U_0T=\begin{pmatrix} \dfrac{3}{14}&\dfrac{9}{14}&\dfrac{1}{7}\end{pmatrix}$
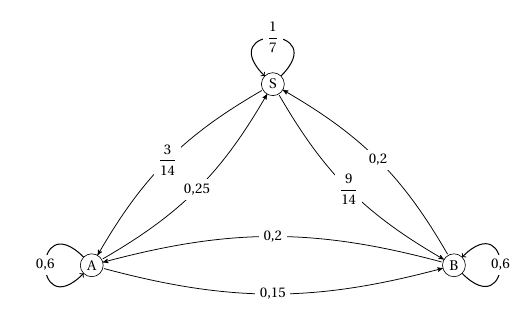
Initialisation : Si $n=0$ on a $U_0=U_0=U_0T^0$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $U_n=U_0T^n$
Montrons que la propriété est vraie au rang suivant, c’est-à-dire que $U_{n+1}=U_0T^{n+1}$
$\begin{align*} U_{n+1}&=U_nT\\
&=U_0TT^n\\
&=U_0T^{n+1}
\end{align*}$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a : $U_n=U_0T^n$.
$\quad$
Au bout d’une semaine on a : $a_1 \approx 0,214$, $b_1\approx 0,643$ et $s_1\approx 0,143$.
$\quad$ - Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.
- On pose $V = \begin{pmatrix}300 &405 &182\end{pmatrix}$.
- Donner, sans détailler les calculs, le produit matriciel $VT$. Que constate-t-on ? On a $VT=\begin{pmatrix}300&405&182\end{pmatrix}=V$
- En déduire un état probabiliste qui reste stable d'un jour sur l'autre. L’état $V$ est donc stable d’un jour sur l’autre.
$\quad$
- On donne l'algorithme suivant, où la commande « $U[i]$ » renvoie le coefficient de la $i$-ème colonne d'une matrice ligne $U$. $$ \begin{array}{ |l|l|}\hline \text{Variables } & k \text{un entier naturel}\\ & U \text{ une matrice de taille } 1 \times 3 \\ & T \text{ une matrice carrée d'ordre } 3\\ \hline \text{Traitement } & U \text{ prend la valeur }\begin{pmatrix}0 &0 &1\end{pmatrix} \\ & T \text{ prend la valeur }\begin{pmatrix}\frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\\frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix} \\ &\text{ Pour } k \text{allant de 1 à 7}\\ &\hspace{1cm} U \text{ prend la valeur } UT \\ &\text{Fin Pour}\\ \hline \text{ Sortie }&\text{Afficher }U[1] \\ \hline \end{array} $$
- Quelle est la valeur numérique arrondie au millième de la sortie de cet algorithme ? L'interpréter dans le contexte de l'exercice. L’algorithme affiche donc $a_7 \approx 0,338$.
- Recopier et modifier cet algorithme pour qu'il affiche la fréquence de joueurs solitaires au bout de $13$ jours. On peut utilise l’algorithme suivant :
Au bout de $7$ jours, environ $33,8\%$ des joueurs sont dans l’équipe A.
$\quad$
Variables :
$\quad$ $k$ un entier naturel
$\quad$ $U$ une matrice de taille $1\times 3$
$\quad$ $T$ une matrice carrée d’ordre $3$
Traitement :
$\quad$ $U$ prend la valeur $\begin{pmatrix}0&0&1\end{pmatrix}$
$\quad$ $T$ prend la valeur $\begin{pmatrix} \dfrac{3}{5}&\dfrac{3}{20}&\dfrac{1}{4}\\
\dfrac{1}{5}&\dfrac{3}{5}&\dfrac{1}{5}\\
\dfrac{3}{14}&\dfrac{9}{14}&\dfrac{1}{7}\end{pmatrix}$
$\quad$ Pour $k$ allant de $1$ à $13$
$\qquad$ $U$ prend la valeur $UT$
$\quad$ Fin Pour
Sortie :
$\quad$ Afficher $U[3]$.
$\quad$
Cela signifie donc que :
$\begin{align*} \dfrac{1}{7}+3p+p=1 &\iff 4p=\dfrac{6}{7} \\
&\iff p=\dfrac{3}{14}
\end{align*}$
$\quad$
- Vues: 76689
