Baccalauréat S Métropole - La Réunion 12 septembre 2017
Exercice 1 6 points
Partie A
On considère la suite $\left(u_n\right)$ définie pour tout entier naturel $n$ par : \[u_n = \displaystyle\int_0^n \text{e}^{ - x^2}\:\text{d}x.\] On ne cherchera pas à calculer $u_n$ en fonction de $n$.
-
- Montrer que la suite $\left(u_n\right)$ est croissante.
- Démontrer que pour tout réel $x \geqslant 0$, on a : $- x^2 \leqslant - 2x + 1$, puis : $\text{e}^{- x^2} \leqslant \text{e}^{-2x+1}$. En déduire que pour tout entier naturel $n$, on a : $u_n < \dfrac{\text{e}}{2}$.
- Démontrer que la suite $\left(u_n\right)$ est convergente. On ne cherchera pas à calculer sa limite.
- Dans cette question, on se propose d'obtenir une valeur approchée de $u_2$. Dans le repère orthonormé $\left(\text{O}~;~\vec{\imath},~ \vec{\jmath}\right)$ ci-dessous, on a tracé la courbe $\mathcal{C}_f$ représentative de la fonction $f$ définie sur l'intervalle [0~;~2] par $f(x) = \text{e}^{- x^2}$, et le rectangle OABC où A$(2~;~0)$, B$(2~;~1)$ et C$(0~;~1)$. On a hachuré le domaine $\mathcal{D}$ compris entre la courbe $\mathcal{C}_f$, l'axe des abscisses, l'axe des ordonnées et la droite d'équation $x = 2$.
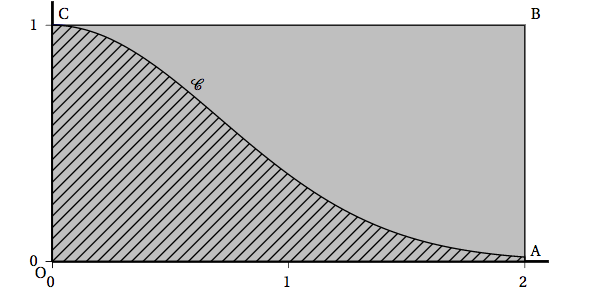
On considère l'expérience aléatoire consistant à choisir un point $M$ au hasard à l'intérieur du rectangle OABC. On admet que la probabilité $p$ que ce point appartienne au domaine est : $p = \dfrac{\text{aire de } \mathcal{D}}{\text{aire de OABC}}$.- Justifier que $u_2 = 2p$.
- On considère l'algorithme suivant: $$ \begin{array}{|c|l|}\hline L1 & \text{Variables} : N,\: C \text{ nombres entiers} ; X,\: Y,\: F \text{ nombres réels}\\ L2 & \text{Entrée} : \text{ Saisir } N \\ L3 &\text{Initialisation} : C \text{ prend la valeur } 0 \\ L4 &\text{Traitement} : \\ L5 & \text{Pour } k \text{ variant de 1 à } N \\ L6 &\quad X \text{ prend la valeur d'un nombre aléatoire entre 0 et 2 } \\ L7 &\quad Y \text{ prend la valeur d'un nombre aléatoire entre 0 et 1 }\\ L8 &\quad \text{ Si } Y \leqslant \text{e}^{- x^2} \text{ alors }\\ L9 &\quad \quad \quad C \text{ prend la valeur } C+ 1 \\ L10 &\quad \text{ Fin si } \\ L11 & \text{Fin pour }\\ L12 & \text{Afficher }C \\ L13 & F \text{ prend la valeur } C/N \\ L14 & \text{Afficher } F \\ \hline \end{array} $$
- Que permet de tester la condition de la ligne L8 concernant la position du point $M(X~;~ Y)$ ?
- Interpréter la valeur $F$ affichée par cet algorithme.
- Que peut-on conjecturer sur la valeur de $F$ lorsque $N$ devient très grand ?
- En faisant fonctionner cet algorithme pour $N = 10^6$, on obtient $C = 441\;138$. On admet dans ce cas que la valeur $F$ affichée par l'algorithme est une valeur approchée de la probabilité $p$ à $10^{-3}$ près. En déduire une valeur approchée de $u_2$ à $10^{-2}$ près.
Partie B
Une entreprise spécialisée est chargée par l'office de tourisme d'une station de ski de la conception d'un panneau publicitaire ayant la forme d'une piste de ski. Afin de donner des informations sur la station, une zone rectangulaire est insérée sur le panneau comme indiqué sur la figure ci-dessous. 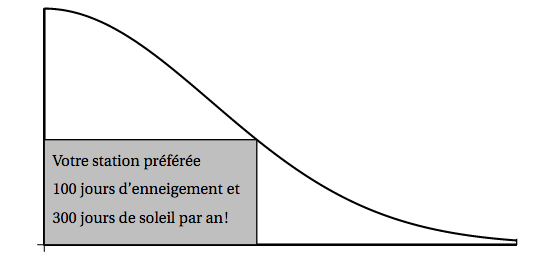
Le panneau, modélisé par le domaine $\mathcal{D}$ défini dans la partie A, est découpé dans une plaque rectangulaire de 2 mètres sur 1 mètre. Il est représenté ci-dessous dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j}\right)$ ; l'unité choisie est le mètre.
Pour $x$ nombre réel appartenant à l'intervalle $[0~;~2]$, on note :
- $M$ le point de la courbe $\mathcal{C}_f$ de coordonnées $\left(x~;~\text{e}^{-x^2}\right)$,
- $N$ le point de coordonnées $(x~;~0)$,
- $P$ le point de coordonnées $\left(0~;~\text{e}^{-x^2}\right)$,
- $A(x)$ l'aire du rectangle O$NMP$.
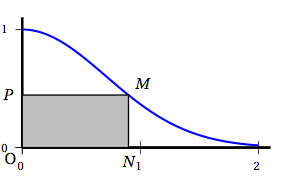
- Justifier que pour tout nombre réel $x$ de l'intervalle [0~;~2], on a: $A(x) = x\text{e}^{- x^2}$.
- Déterminer la position du point $M$ sur la courbe $\mathcal{C}_f$ pour laquelle l'aire du rectangle O$NMP$ est maximale.
- Le rectangle O$NMP$ d'aire maximale obtenu à la question 2. doit être peint en bleu, et le reste du panneau en blanc. Déterminer, en m$^2$ et à $10^{-2}$ près, la mesure de la surface à peindre en bleu et celle de la surface à peindre en blanc.
- Vues: 44505
