Baccalauréat S Métropole - La Réunion 12 septembre 2017 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Probabilités

Tous les résultats demandés seront arrondis au millième.

1. Une étude effectuée sur une population d'hommes âgés de 35 à 40 ans a montré que le taux de cholestérol total dans le sang, exprimé en grammes par litre, peut être modélisé par une variable aléatoire $T$ qui suit une loi normale d'espérance $\mu = 1,84$ et d'écart type $\sigma = 0,4$.
   1. Déterminer selon cette modélisation la probabilité qu'un sujet tiré au hasard dans cette population ait un taux de cholestérol compris entre $1,04$g /L et $2,64$ g/L.
   On veut calculer $P(1,04 \leq p T \leq 2,64) = P(\mu-2\sigma \leq T \leq \mu +2\sigma) \approx 0,954$
   $\quad$
   

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

   2. Déterminer selon cette modélisation la probabilité qu'un sujet tiré au hasard dans cette population ait un taux de cholestérol supérieur à $1,2$ g/L.
   $P(T \geq 1,2)=0,5+P(1,2 \leq p T \leq p 1,84) \approx 0,945$
   

    

   2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

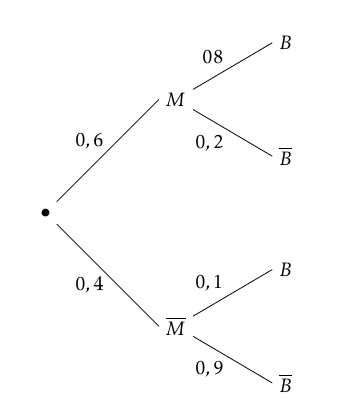
   $$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2. Afin de tester l'efficacité d'un médicament contre le cholestérol, des patients nécessitant d'être traités ont accepté de participer à un essai clinique organisé par un laboratoire. Dans cet essai, 60 % des patients ont pris le médicament pendant un mois, les autres ayant pris un placebo (comprimé neutre). On étudie la baisse du taux de cholestérol après l'expérimentation. On constate une baisse de ce taux chez 80 % des patients ayant pris le médicament. On ne constate aucune baisse pour 90 % des personnes ayant pris le placebo. On choisit au hasard un patient ayant participé à l'expérimentation et on note :
   • $M$ l'évènement « le patient a pris le médicament» ;
   • $B$ l'évènement « le taux de cholestérol a baissé chez le patient ».
   1. Traduire les données de l'énoncé à l'aide d'un arbre pondéré.
   
   2. Calculer la probabilité de l'évènement $B$.
   D’après la formule des probabilités totales on a :
   $\begin{align*} p(B)&=p(M\cap B)+p\left(\overline{M}\cap B\right) \\
   &=0,6\times 0,8+0,4\times 0,1 \\
   &=0,52
   \end{align*}$
   
   3. Calculer la probabilité qu'un patient ait pris le médicament sachant que son taux de cholestérol a baissé.
   On veut calculer :
   $\begin{align*} p_B(M)&=\dfrac{p(M\cap B)}{p(B)} \\
   &=\dfrac{0,6\times 0,8}{0,52} \\
   &=\dfrac{12}{13} \\
   &\approx 0,923
   \end{align*}$
3. Le laboratoire qui produit ce médicament annonce que 30 % des patients qui l'utilisent présentent des effets secondaires. Afin de tester cette hypothèse, un cardiologue sélectionne de manière aléatoire $100$ patients traités avec ce médicament.
   1. Déterminer l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de patients suivant ce traitement et présentant des effets secondaires.

   La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
   Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

   En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$

   
   L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

   $\begin{align*} I_{100}&\approx [0,210;0,390]
   \end{align*}$
   $\quad$
   
   2. L'étude réalisée auprès des $100$ patients a dénombré $37$  personnes présentant des effets secondaires. Que peut-on en conclure ?
   La fréquence observée est $f=0,37\in I_{100}$
   Au risque d’erreur de $5\%$, on ne peut pas rejeter l’annonce du laboratoire.
   
   3. Pour estimer la proportion d'utilisateurs de ce médicament présentant des effets secondaires, un organisme indépendant réalise une étude basée sur un intervalle de confiance au niveau de confiance 95 %. Cette étude aboutit à une fréquence observée de 37 % de patients présentant des effets secondaires, et à un intervalle de confiance qui ne contient pas la fréquence 30 %. Quel est l'effectif minimal de l'échantillon de cette étude ?
   Un intervalle de confiance est de la forme $\left[f-\dfrac{1}{\sqrt{n}};f+\dfrac{1}{\sqrt{n}}\right]$
   On sait que $0,37$ appartient à cet intervalle mais pas $0,30$.
   Par conséquent, on cherche le plus petit entier naturel $n$ tel que :
   $\begin{align*} 0,3 < 0,37-\dfrac{1}{\sqrt{n}}&\iff -0,07 < -\dfrac{1}{\sqrt{n}} \\
   &\iff \sqrt{n} > \dfrac{1}{0,07} \\
   &\iff n > \dfrac{1}{0,07^2} \\
   &\iff n \geq 205
   \end{align*}$