Baccalauréat S Centres étrangers 13 juin 2017 - Exercice 4

Page 7 sur 10: Exercice 4

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour tout entier $n \geqslant 4$, on considère $P_n$ un polygone régulier à $n$ côtés, de centre O et dont l'aire est égale à 1. On admet qu'un tel polygone est constitué de $n$ triangles superposables à un triangle OA$_n$B$_n$ donné, isocèle en O. On note $r_n = \text{OA}_n$ la distance entre le centre O et le sommet A$_n$ d'un tel polygone.

Partie A : étude du cas particulier $n = 6$

On a représenté ci-dessous un polygone $P_6$.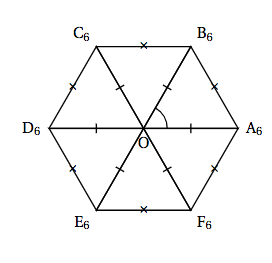

1. Justifier le fait que le triangle OA$_6$B$_6$ est équilatéral, et que son aire est égale à $\dfrac{1}{6}$.
2. Exprimer en fonction de $r_6$ la hauteur du triangle OA$_6$B$_6$ issue du sommet B$_6$.
3. En déduire que $r_6 = \sqrt{\dfrac{2}{3\sqrt{3}}}$.

 

Partie B : cas général avec $n \geqslant 4$

Dans cette partie, on considère le polygone $P_n$ avec $n \geqslant 4$, construit de telle sorte que le point A$_n$ soit situé sur l'axe réel, et ait pour affixe $r_n$. On note alors $r_n \mathrm{e}^{\text{i}\theta_n}$ l’affixe de B$_n$ où $\theta_n$ est un réel de l'intervalle $\left]0~;~\dfrac{\pi}{2}\right]$.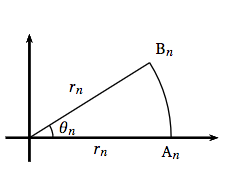

1. Exprimer en fonction de $r_n$ et $\theta_n$ la hauteur issue de B$_n$ dans le triangle OA$_n$B$_n$ puis établir que l'aire de ce triangle est égale à $\dfrac{r_n^2}{2} \sin \left(\theta_n \right)$.
2. On rappelle que l'aire du polygone $P_n$ est égale à 1. Donner, en fonction de $n$, une mesure de l'angle $\left(\vec{\text{OA}_n},~\vec{\text{OB}_n}\right)$, puis démontrer que : \[r_n = \sqrt{\dfrac{2}{n \sin \left(\dfrac{2\pi}{n}\right)}}.\]

 

Partie C : étude de la suite $\left(r_n\right)$

On considère la fonction $f$ définie pour tout réel $x$ de l'intervalle $]0~;~\pi[$ par \[f(x) = \dfrac{x}{\sin x}.\] Ainsi, le nombre $r_n$, défini dans la partie B pour $n \geqslant 4$, s'exprime à l'aide de la fonction $f$ par : \[r_n=\sqrt{\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n}\right)}.\] On admet que la fonction $f$ est strictement croissante sur l'intervalle $]0~;~\pi[$.

1. Montrer que la suite $\left(r_n\right)$ est décroissante. On pourra pour cela commencer par démontrer que pour tout $n \geqslant 4$, on a : $0 < \dfrac{2\pi}{n+1} < \dfrac{2\pi}{n} < \pi$.
2. En déduire que la suite $\left(r_n\right)$ converge. On ne demande pas de déterminer sa limite $L$, et on admet dans la suite de l'exercice que $L = \dfrac{1}{\sqrt{\pi}}$.
3. On considère l'algorithme suivant. $$\begin{array}{|l |l |}\hline \text{VARIABLES: } & n \text{ est un nombre entier }\\ \text{ TRAITEMENT : }& n \text{ prend la valeur 4 }\\ &\text{Tant que } \sqrt{\dfrac{2}{n \sin \left(\dfrac{2\pi}{n}\right)}}> 0,58 \text{ faire }\\ &\hspace{1cm} n \text{ prend la valeur }n + 1 \\ &\text{ Fin Tant que }\\ \text{SORTIE : } &\text{Afficher }n \\ \hline \end{array}$$ Quelle valeur numérique de $n$ va afficher en sortie cet algorithme ?