Baccalauréat STI2D - STL Polynésie 16 juin 2014 spécialité SPCL

Exercice 1 4 points

QCM nombres complexes et équations différentielles

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent aucun point.
  Indiquer sur la copie la réponse choisie Dans les questions 1. et 2., on considère le complexe $z = - 2\text{e}^{-2\text{i}\frac{\pi}{3}}$.

1. Le complexe $z^3$ est égal à :
   1. 8
   2. $-8$
   3. $8\text{i}$
   4. $- 8\text{i}$
2. Un argument de $z$ est
   1. $- \dfrac{2\pi}{3}$
   2. $\dfrac{2\pi}{3}$
   3. $- \dfrac{\pi}{3}$
   4. $\dfrac{\pi}{3}$
3. On considère l'équation différentielle $y' - 3y = 2$, où $y$ désigne une fonction dérivable sur l'ensemble des réels. Une solution $f$ de cette équation est la fonction de la variable $x$ vérifiant pour tout réel $x$ :
   1. $f(x) = 2\text{e}^{-3x}$
   2. $f(x) = \text{e}^{3x} + \dfrac{2}{3}$
   3. $f(x) = \text{e}^{\frac{2}{3}x}$
   4. $f(x) = \text{e}^{3x} - \dfrac{2}{3}$
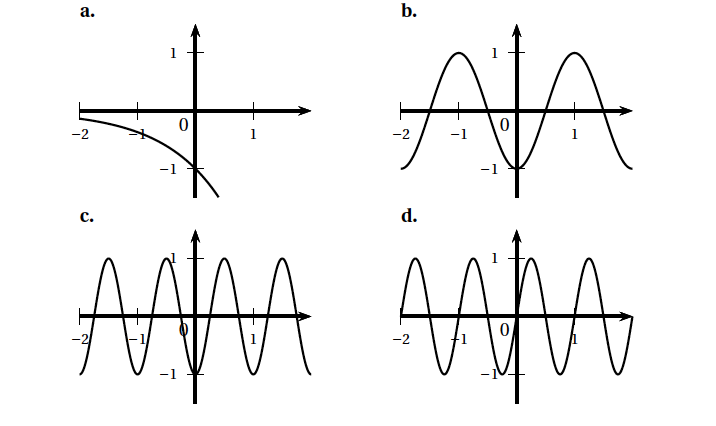
4. La solution $f$ de l'équation différentielle $y'' + 4\pi^2 y = 0$ qui vérifie $f(0) = - 1$ et $f'(0) = 0$ admet comme représentation graphique :
   

Correction de l'Exercice 1 4 points

QCM nombres complexes et équations différentielles

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent aucun point.
  Indiquer sur la copie la réponse choisie Dans les questions 1. et 2., on considère le complexe $z = - 2\text{e}^{-2\text{i}\frac{\pi}{3}}$.

1. Le complexe $z^3$ est égal à : $$\begin{array}{ll } \\ z^3 & =\left (- 2\text{e}^{ \text{i}\frac{\pi}{3}}\right )^3 \\ &=(-2)^3 \times \left (- 2\text{e}^{-2\text{i}\frac{\pi}{3}}\right )^3 \\& =-8 \times \text{e}^{-6\text{i}\frac{\pi}{3}} \\ & =-8 \times \text{e}^{ \text{i}2 \pi}\\ & =-8 \times \text{e}^{ \text{i}\times 0}\\ & =-8 \\ \end{array}$$
   1. FAUX
   2. VRAI :$-8$
   3. FAUX
   4. FAUX
2. Comme $\text{e}^{ \text{i} \pi}=-1$ alors la forme exponentielle de $z$ est : $z=- 2\text{e}^{-2\text{i}\frac{\pi}{3}}=2\text{e}^{-2\text{i}\frac{\pi}{3}}\times (-1) =2\text{e}^{-2\text{i}\frac{\pi}{3}}\times \text{e}^{ \text{i} \pi}=2\text{e}^{\text{i}\frac{\pi}{3}} $
   Un argument de $z$ est $\dfrac{\pi}{3}$
   1. FAUX
   2. FAUX
   3. FAUX
   4. VRAI :$\dfrac{\pi}{3}$
3. On considère l'équation différentielle $y' - 3y = 2$, où $y$ désigne une fonction dérivable sur l'ensemble des réels.
   L'équation différentielle $y'-3y=2$ se met sous la forme $y'=3y+2$. Elle est de la forme $y'=ay+b$ avec $a=3$ et $b=2$. Les solutions de cette équation sont les fonctions de la forme $x \mapsto k \text{e}^{3x} - \dfrac{2}{3} $, où k est une constante réelle. Donc en choisissant $k=1$, la fonction $f$ définie pour tout réel $x$ par $f(x) = \text{e}^{3x} - \dfrac{2}{3}$ est une solution de cette équation. Une solution $f$ de cette équation est la fonction de la variable $x$ vérifiant pour tout réel $x$ :
   1. FAUX
   2. FAUX
   3. FAUX
   4. VRAI :$f(x) = \text{e}^{3x} - \dfrac{2}{3}$
4. La solution $f$ de l'équation différentielle $y'' + 4\pi^2 y = 0$ qui vérifie $f(0) = - 1$ et $f'(0) = 0$ admet comme représentation graphique :
   • Les conditions initiales $f(0)=-1$ et $f'(0)=0$ permettent d'éliminer les courbes proposées en a. et d.
   • L'équation différentielle $y'' + 4\pi^2 y = 0$ est de la forme $y'' + \omega ^2 y = 0$ avec $\omega ^2= 4\pi^2$.
     En prenant $\omega =2\pi$, les solutions de cette équation sont les fonctions de la forme $x \mapsto A \cos\left (2\pi x\right )+ B\sin\left (2\pi x\right )$, où $A$ et $B$ sont deux une constantes réelles.
   • $f(0)=-1$ d'où $A \cos\left (0\right )+ B\sin\left (0\right )=-1$ donc $A=-1$.
     Soit $f: x \mapsto \cos\left (2\pi x\right )+ B\sin\left (2\pi x\right )$. Par conséquent, $f(1)= -\cos\left (2\pi \right )+ B\sin\left (2\pi \right )=-1+ B \times 0=-1$.
   La courbe c. est la seule qui puisse convenir.
   
   

Exercice 2 4 points

Suites

«  En 2009, les Français ont en moyenne produit $374$ kg de déchets ménagers par habitant. »  Source Ademe
Le maire d'une commune de 53700 habitants constata avec déception que ses administrés avaient produit 23000 tonnes de déchets en 2009, Il décida alors de mettre en place une nouvelle campagne de sensibilisation au recyclage des papiers, plastiques, verres et métaux.
Cela permit à la ville d'atteindre $400$ kg de déchets ménagers en moyenne par habitant en 2011 et d'espérer réduire ensuite cette production de 1,5 % par an pendant 5 ans.

1. Justifier la déception du maire en 2009.
2. On note $d_{0} = 400$. Pour tout nombre entier naturel non nul $n$, on note $d_{n}$ la quantité (en kg) de déchets ménagers produite par habitant de cette ville durant l'année $2011 + n$.
   1. Montrer que $d_{1} = 0, 985d_{0}$.
   2. Déterminer la nature de la suite $\left(d_{n}\right)$. Exprimer $d_{n}$ en fonction de $n$ puis calculer la limite de la suite $\left(d_{n}\right)$.
   3. Quelle devrait être, à ce rythme là , la production en kilogrammes de déchets ménagers par habitant dans cette ville en 2014 ?
3. On considère l'algorithme suivant : $$ \begin{array}{|l |l |}\hline & \text{ Les variables sont l'entier naturel } N \text{ et le réel } d. \\ \text{ Initialisation :}& \text{ Affecter à } N \text{ la valeur 0 }\\ &\text{ Affecter à } d \text{ la valeur 400 }\\ \text{ Traitement :}& \text{ Tant que }d > 374\\ & \text{ Affecter à } N \text{ la valeur } N + 1\\ & \text{ Affecter à } d \text{ la valeur } 0,985d\\ &\text{ Fin Tant que }\\ \text{ Sortie : }& \text{ Afficher } N \\\hline \end{array}$$ Donner la valeur affichée pour $N$ et interpréter ce résultat.

Exercice 2 4 points

Suites

«  En 2009, les Français ont en moyenne produit $374$ kg de déchets ménagers par habitant. »  Source Ademe
Le maire d'une commune de 53700 habitants constata avec déception que ses administrés avaient produit 23000 tonnes de déchets en 2009, Il décida alors de mettre en place une nouvelle campagne de sensibilisation au recyclage des papiers, plastiques, verres et métaux.
Cela permit à la ville d'atteindre $400$ kg de déchets ménagers en moyenne par habitant en 2011 et d'espérer réduire ensuite cette production de 1,5 % par an pendant 5 ans.

1. Justifier la déception du maire en 2009.

En 2009, la quantité moyenne (en kg) de déchets ménagers produite par habitant était : $\dfrac{23000 \times 1000}{53700} \approx 438 $
En 2009, les habitants de cette commune ont en moyenne produit 438 kg de déchets ménagers par habitant, d'où la déception du maire.
2. On note $d_{0} = 400$. Pour tout nombre entier naturel non nul $n$, on note $d_{n}$ la quantité (en kg) de déchets ménagers produite par habitant de cette ville durant l'année $2011 + n$.
   1. Montrer que $d_{1} = 0, 985d_{0}$.
   
   À partir de 2011, la quantité de déchets ménagers produite par habitant est réduite de 1,5 % par an pendant 5 ans d'où :
   $$d_1=400\times \left (1-\dfrac{1,5}{100}\right) =400\times 0 ,985=0,985 d_0$$
   Ainsi, $d_1=0,985 d_0$
   2. Déterminer la nature de la suite $\left(d_{n}\right)$. Exprimer $d_{n}$ en fonction de $n$ puis calculer la limite de la suite $\left(d_{n}\right)$.
   
   
   • Pour tout nombre entier naturel $n, d_{n+1}=0,985 d_n$ donc $\left (d_n\right )$ est une suite géométrique de raison 0,985.
   • $\left (d_n\right )$ est une suite géométrique de raison 0,985 et de premier terme $d_0=400$
     donc pour tout entier $n, d_n=q^n \times d_0= 400\times 0,985^n$.
   • $0 < 0,985 < 1 $ donc $\lim\limits_{n \to +\infty}~ 0,985^n=0$ d'où, $\lim\limits_{n \to +\infty}~ 400\times0,985^n=0$. Soit $\lim\limits_{n \to +\infty}~ d_n=0$
     donc la suite $\left (d_n\right )$ converge vers 0.
   3. Quelle devrait être, à ce rythme là , la production en kilogrammes de déchets ménagers par habitant dans cette ville en 2014 ?
   
   $$d_3=400\times 0,985^3 \approx 382$$
   Selon ce modèle, la production de déchets ménagers par habitant dans cette ville en 2014 est de 382 kg.


3. On considère l'algorithme suivant : $$ \begin{array}{|l |l |}\hline & \text{ Les variables sont l'entier naturel } N \text{ et le réel } d. \\ \text{ Initialisation :}& \text{ Affecter à } N \text{ la valeur 0 }\\ &\text{ Affecter à } d \text{ la valeur 400 }\\ \text{ Traitement :}& \text{ Tant que }d > 374\\ & \text{ Affecter à } N \text{ la valeur } N + 1\\ & \text{ Affecter à } d \text{ la valeur } 0,985d\\ &\text{ Fin Tant que }\\ \text{ Sortie : }& \text{ Afficher } N \\\hline \end{array}$$ Donner la valeur affichée pour $N$ et interpréter ce résultat.

$N$ est égal au plus petit entier $n$ solution de l'inéquation $400 \times 0,985^n \leq 374$ $$\begin{array}{lll} \\ 400 \times 0,985^n \leq 374 & \iff 0,985^n \leq \dfrac{374}{400} & \\ & \iff \ln\left (0,985^n\right ) \leq \ln\left (\dfrac{374}{400}\right ) & \text{ La fonction } \ln \text{ est strictement croissante sur } ]0~;~+ \infty[ \\ & \iff n \ln\left (0,985 \right ) \leq \ln\left (\dfrac{374}{400}\right ) & \text{ car } \ln\left (a^n\right )=n\ln a\\ & \iff n \geq \dfrac{\ln\left (\dfrac{374}{400}\right )}{\ln\left (0,985 \right ) } & \ln\left (0,985 \right ) < 0 \\ \end{array}$$ Comme $\dfrac{\ln\left (\dfrac{374}{400}\right )}{\ln\left (0,985 \right ) }\approx 4,4$ , le plus petit entier que $400 \times 0,985^n \leq 374$ est 5.
La valeur affichée est $N=5$. C'est en 2016 que la quantité de déchets ménagers produite par habitant de cette ville sera inférieure à 374 kg.

Exercice 3 5 points

Probabilités

Les trois parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis à $10^{-3}$ près.
Une entreprise produit en grande quantité des emballages alimentaires de forme cubique en polypropylène.
Elle utilise pour cela la technique du thermoformage, qui consiste à chauffer une plaque de plastique puis à la former à l'aide d'un moule.
Lors du refroidissement, la pièce rétrécit légèrement mais conserve la forme du moule.
L'objectif de cet exercice est d'analyser la qualité d'une production de boîtes cubiques.

A. Loi normale
Une boîte est jugée conforme lorsque la mesure de son arête, exprimée en millimètres, appartient à l'intervalle [16,7;17,3].
La mesure de l'arête d'une boîte est modélisée par une variable aléatoire $C$ qui suit la loi normale d'espérance $17$ et d'écart type $0,14$.

1. Calculer $P(16, 7 \leqslant C \leqslant 17,3)$.
2. Déterminer la probabilité qu'une boîte prélevée au hasard dans la production soit non conforme.

B. Loi binomiale
L'entreprise conditionne ces boîtes par lots de $200$. On prélève au hasard une boîte dans la production.
On note $p$ la probabilité de l'évènement : «  la boîte prélevée au hasard dans la production est non conforme » .
On prélève au hasard $200$ boîtes dans la production. La production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage aléatoire avec remise.
On considère la variable aléatoire $X$ qui, à un lot de $200$ boîtes., associe le nombre de boîtes non conformes qu'il contient.
On admet que $X$ suit une loi binomiale de paramètres $200$ et $p$, et, qu'en moyenne chaque lot de $200$ boîtes. en contient 6 non conformes.

1. Justifier que $p = 0,03$.
2. Calculer la probabilité qu'il y ait au moins deux boîtes non conformes dans ce lot de $200$ boîtes..

C. Intervalle de fluctuation
On rappelle que, pour une proportion $p$ connue dans une production, l'intervalle de fluctuation asymptotique à 95 % d'une fréquence calculée sur un échantillon de taille $n$ est :
$$I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}};p + 1,96\sqrt{\dfrac{p(1 - p)}{n}} \right]$$
Dans le cadre d'un fonctionnement correct du thermoformage, on admet que la proportion $p$ de boîtes non conformes dans la production est 3 %.

1. Déterminer les bornes de l'intervalle $I$ pour un échantillon de taille $200$.
2. On contrôle le bon fonctionnement du thermoformage en prélevant au hasard dans la production des échantillons de $200$ boîtes.
   Au cours de l'un de ces contrôles, un technicien a compté $10$ boîtes non conformes.
   Doit-il prendre la décision d'effectuer des réglages sur la thermoformeuse ? Justifier la réponse.

Exercice 3 5 points

Probabilités

Les trois parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis à $10^{-3}$ près.
Une entreprise produit en grande quantité des emballages alimentaires de forme cubique en polypropylène.
Elle utilise pour cela la technique du thermoformage, qui consiste à chauffer une plaque de plastique puis à la former à l'aide d'un moule.
Lors du refroidissement, la pièce rétrécit légèrement mais conserve la forme du moule.
L'objectif de cet exercice est d'analyser la qualité d'une production de boîtes cubiques.

A. Loi normale
Une boîte est jugée conforme lorsque la mesure de son arête, exprimée en millimètres, appartient à l'intervalle [16,7;17,3].
La mesure de l'arête d'une boîte est modélisée par une variable aléatoire $C$ qui suit la loi normale d'espérance $17$ et d'écart type $0,14$.

1. Calculer $P(16, 7 \leqslant C \leqslant 17,3)$.

2ND   DISTR   2 NORMALCDF( 16.7  , 17.3,17   ,0.14)EXE 

$Normalcdf(16.7,17.3,17,0.14) \approx 0,968$

$P(16, 7 \leqslant C \leqslant 17,3) \approx 0,968$.
La probabilité qu'une boîte prélevée au hasard dans la production soit conforme est égale à 0,968 à $10^{-3}$ près.
2. Déterminer la probabilité qu'une boîte prélevée au hasard dans la production soit non conforme.

$P( C\notin [16, 7 ; 17,3]) =1-P(16, 7 \leqslant C \leqslant 17,3)\approx 0,032 $
La probabilité qu'une boîte prélevée au hasard dans la production soit non conforme est égale à 0,032 à $10^{-3}$ près.

B. Loi binomiale
L'entreprise conditionne ces boîtes par lots de $200$. On prélève au hasard une boîte dans la production.
On note $p$ la probabilité de l'évènement : «  la boîte prélevée au hasard dans la production est non conforme » .

On prélève au hasard $200$ boîtes dans la production. La production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage aléatoire avec remise.
On considère la variable aléatoire $X$ qui, à un lot de $200$ boîtes., associe le nombre de boîtes non conformes qu'il contient.

On admet que $X$ suit une loi binomiale de paramètres $200$ et $p$, et, qu'en moyenne chaque lot de $200$ boîtes en contient 6 non conformes.

1. Justifier que $p = 0,03$.


En moyenne, chaque lot de 200 boîtes en contient 6 non conformes d'où $p=\dfrac{6}{200}=0,03$.
2. Calculer la probabilité qu'il y ait au moins deux boîtes non conformes dans ce lot de $200$ boîtes.

$X$ suit une loi binomiale de paramètres $n=200$ et $p=0,03$ $P(X\geq 2)=1-P(X\leq 1)\approx 0,984$
La probabilité qu'il y ait au moins deux boîtes non conformes dans ce lot de 200 boîtes est égale à 0,984 à $10^{-3}$ près.

C. Intervalle de fluctuation
On rappelle que, pour une proportion $p$ connue dans une production, l'intervalle de fluctuation asymptotique à 95 % d'une fréquence calculée sur un échantillon de taille $n$ est :
$$I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}};p + 1,96\sqrt{\dfrac{p(1 - p)}{n}} \right]$$
Dans le cadre d'un fonctionnement correct du thermoformage, on admet que la proportion $p$ de boîtes non conformes dans la production est 3 %.

1. Déterminer les bornes de l'intervalle $I$ pour un échantillon de taille $200$.

Comme $n=200, n \times p=200\times 0,03=6$ et $n \times(1-p)=200\times 0,97=194$, les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies. L'intervalle de fluctuation asymptotique au seuil 0,95 est : $$I = \left[0,03 - 1,96\sqrt{\dfrac{0,03\times 0,97}{200}}~;~0,03 + 1,96\sqrt{\dfrac{0,03\times 0,97}{200}} \right]$$
Soit avec des valeurs approchées à $10^{-3}$ près des bornes de l'intervalle, l'intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence de boîtes non conformes dans la production sur un échantillon de taille 200 est $I=[0,006;0,054]$.
2. On contrôle le bon fonctionnement du thermoformage en prélevant au hasard dans la production des échantillons de $200$ boîtes.
   Au cours de l'un de ces contrôles, un technicien a compté $10$ boîtes non conformes.
   Doit-il prendre la décision d'effectuer des réglages sur la thermoformeuse ? Justifier la réponse.

La fréquence observée de boîtes non conformes dans la production est $f=\dfrac{10}{200}=0,05$
La fréquence observée appartient à l'intervalle de fluctuation asymptotique au seuil de 95% le technicien n'effectue pas de réglages sur la thermoformeuse.

Exercice 4 7 points

Fonction logarithme

Soit $f$ la fonction définie sur $]0;+\infty[$ par : \[f(x) = 6 \ln x + ax + b\] où $a$ et $b$ sont des constantes réelles.
On appelle $\mathcal{C}_{f}$ la courbe représentative de la fonction $f$ dans un repère orthogonal $\left(\text{O},~\vec{i},\vec{j}\right)$.

• Le point A(1;1) appartient à $\mathcal{C}_{f}$.
• $\mathcal{C}_{f}$ admet une tangente horizontale en son point d'abscisse 2.

PARTIE A

Sur le graphique ci-dessous, on a tracé $\mathcal{C}_{f}$ (trait plein) ainsi que les courbes $\Gamma$ et $\Omega$. L'une de ces deux courbes est la représentation graphique de la fonction dérivée $f'$ de $f$ et l'autre représente une primitive $F$ de $f$.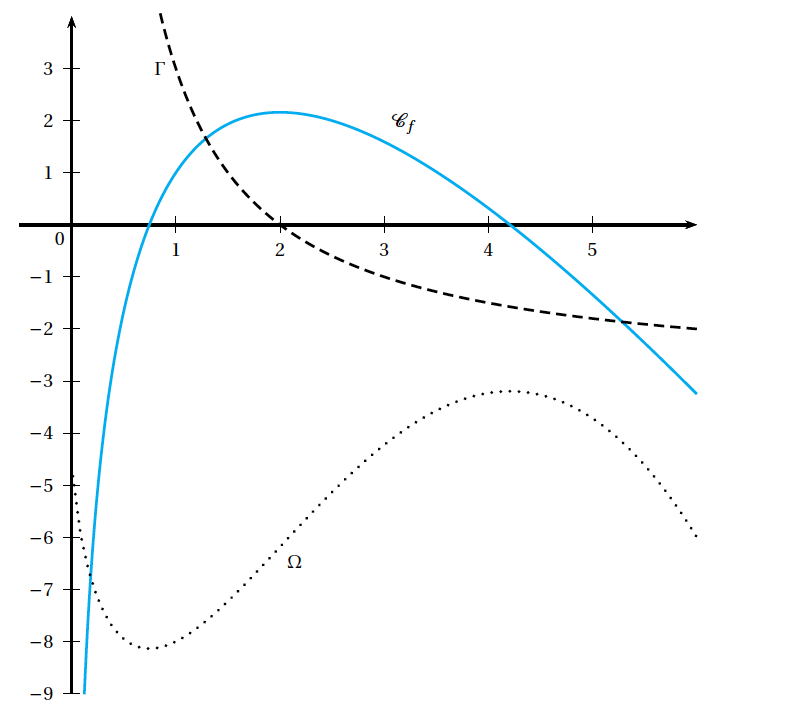

1. Indiquer laquelle des deux courbes est la représentation graphique de $F$.
2. Par lecture graphique, déterminer $f(1)$ et $f'(2)$.
3. Donner l'expression de $f'(x)$ en fonction de $x$ et de $a$.
4. l'aide des résultats précédents, montrer que pour tout $x$ de l'intervalle $]0; + \infty[$, \[f(x) = 6\ln x - 3x + 4.\]

PARTIE B

Dans cette partie, on pourra vérifier la cohérence des résultats obtenus avec la courbe $\mathcal{C}_{f}$ fournie dans la partie A.

1. Calculer la limite de la fonction $f$ lorsque $x$ tend vers $0$. Interpréter graphiquement cette limite.
2. Montrer que pour tout $x$ de l'intervalle $]0; + \infty[ , f'(x) = \dfrac{3}{x}(2 - x).$
3. Étudier le signe de $f'(x)$ puis donner les variations de la fonction $f$.
4. En déduire que la fonction $f$ admet un extremum dont on calculera la valeur exacte.

PARTIE C

Soit $H$ la fonction définie sur $]0; + \infty[$ par: \[H(x) = 6x\ln x - \dfrac{3}{2}x^2 - 2x.\]

1. Montrer que $H$ est une primitive de $f$ sur $]0; + \infty[$.
2. Calculer la valeur exacte de $I = \displaystyle\int_{1}^{\text{e}} f(x)\:\text{dx}.$
3. Donner une interprétation graphique du nombre $I$.
4. 1. l'aide du graphique, donner la valeur de $F(1)$.
   2. En déduire une expression de $F(x)$ pour tout $x$ dans l'intervalle $]0; + \infty[$.

Exercice 4 7 points

Fonction logarithme

Soit $f$ la fonction définie sur $]0;+\infty[$ par : \[f(x) = 6 \ln x + ax + b\] où $a$ et $b$ sont des constantes réelles.
On appelle $\mathcal{C}_{f}$ la courbe représentative de la fonction $f$ dans un repère orthogonal $\left(\text{O},~\vec{i},\vec{j}\right)$.

• Le point A(1;1) appartient à $\mathcal{C}_{f}$.


• $\mathcal{C}_{f}$ admet une tangente horizontale en son point d'abscisse 2.

PARTIE A

Sur le graphique ci-dessous, on a tracé $\mathcal{C}_{f}$ (trait plein) ainsi que les courbes $\Gamma$ et $\Omega$. L'une de ces deux courbes est la représentation graphique de la fonction dérivée $f'$ de $f$ et l'autre représente une primitive $F$ de $f$.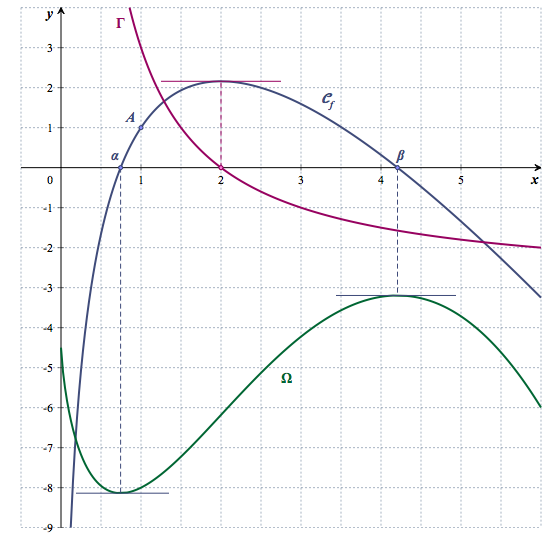

1. Indiquer laquelle des deux courbes est la représentation graphique de $F$.

Dire que $F$ est une primitive de la fonction $f$ signifie que pour tout réel $x$ strictement positif, $F′(x)=f(x)$. Par conséquent, les variations de la fonction $F$ se déduisent du signe de de la fonction $f$.

D'après les variations de la fonction $F, \Omega$ est la courbe représentative de la fonction $F$.
2. Par lecture graphique, déterminer $f(1)$ et $f'(2)$.

D'après les données de l'énoncé :
• Le point A$(1;1)$ appartient à $\mathcal{C}_{f}$ donc $f(1)=1$.
• $\mathcal{C}_{f}$ admet une tangente horizontale en son point d'abscisse 2 donc $f′(2)=0$.
3. Donner l'expression de $f'(x)$ en fonction de $x$ et de $a$.


$f'$ est la fonction définie sur $]0~;~+\infty[$ par $f'(x)=\dfrac{6}{x}+a.$
4. l'aide des résultats précédents, montrer que pour tout $x$ de l'intervalle $]0; + \infty[$, \[f(x) = 6\ln x - 3x + 4.\]



• Comme $f'(2)=0$ alors, $\dfrac{6}{2}+a=0$ soit $3+a=0$
• Comme $f(1)=1$ alors, $6 \ln 1 + a \times 1 + b=0$ soit $a+b=1$
Ainsi, $a$ et $b$ sont solutions du système :$$ \left\lbrace\begin{array}{ll} 3+a&=0\\ ~a+b &=1\\ \end{array} \right.\iff \left\lbrace\begin{array}{ll} a&=-3\\ ~ b &=4\\ \end{array} \right.$$
$f$ est la fonction définie sur $]0~;~ + \infty[$ par $f(x) = 6 \ln x -3x + 4.$

PARTIE B

Dans cette partie, on pourra vérifier la cohérence des résultats obtenus avec la courbe $\mathcal{C}_{f}$ fournie dans la partie A.

1. Calculer la limite de la fonction $f$ lorsque $x$ tend vers $0$. Interpréter graphiquement cette limite.

$\left.\begin{array}{l} \lim\limits_{x \to 0^+}~\ln x=-\infty\\ \lim\limits_{x \to 0^+}~-3x + 4=4\end{array}\right\}$ par somme on obtient : $\lim\limits_{x \to 0^+}f(x) = -\infty$
$\lim\limits_{x \to 0^+} f(x) = -\infty$ par conséquent, la courbe $\mathcal{C}_{f}$ admet pour asymptote l'axe des ordonnées.
2. Montrer que pour tout $x$ de l'intervalle $]0; + \infty[ , f'(x) = \dfrac{3}{x}(2 - x).$

Pour tout réel $x $ de l'intervalle $]0~;~ + \infty[$ , $f'(x)= \dfrac{6}{x}-3= \dfrac{3}{x} (2-x)$
$f'$ est la fonction définie sur $]0~;~ + \infty[$ par $f'(x)= \dfrac{3}{x} (2-x)$.
3. Étudier le signe de $f'(x)$ puis donner les variations de la fonction $f$.

Comme $x > 0$ alors, $f'(x)$ est du même signe que $2-x$.
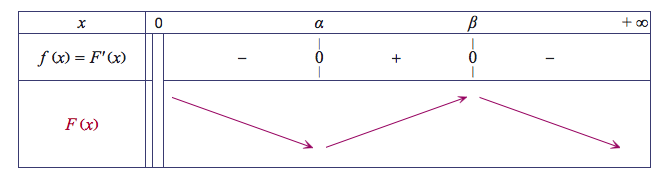
D'où le tableau établissant le signe de $f'(x)$ ainsi que les variations de la fonction $f$ :



4. En déduire que la fonction $f$ admet un extremum dont on calculera la valeur exacte.

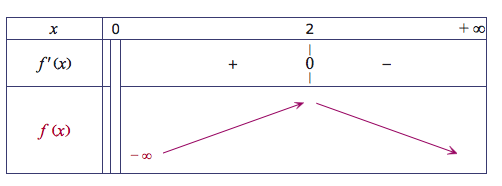
D'après les variations de la fonction $f$, la fonction $f$ admet un maximum pour $x=2$ et $f(2)=6\ln2-2$.
Le maximum de la fonction $f$ est égal à $6\ln2-2$.
 

PARTIE C

Soit $H$ la fonction définie sur $]0; + \infty[$ par: \[H(x) = 6x\ln x - \dfrac{3}{2}x^2 - 2x.\]

1. Montrer que $H$ est une primitive de $f$ sur $]0; + \infty[$.

Pour tout réel $x$ de l'intervalle $]0~;~ + \infty[$, $$ \begin{array}{ll} H'(x)& =6 \times \ln x +6x\times \dfrac{1}{x} -\dfrac{3}{2} \times 2x -2~\\ & =6 \ln x +6-3x-2\\ & =6 \ln x -3x+4\\ & =f(x) \end{array} $$
Pour tout réel $x$ strictement positif, $H′(x)=f(x)$. Par conséquent, la fonction $H$ définie sur$]0~;~ + \infty[$ par $H(x) = 6x\ln x - \dfrac{3}{2}x^2 - 2x$ est une primitive de la fonction $f$.
2. Calculer la valeur exacte de $I = \displaystyle\int_{1}^{\text{e}} f(x)\:\text{dx}.$

$$\begin{array}{ll} I&= \displaystyle\int_{1}^{\text{e}}f(x)\:\text{d}x\\ & = \left [ H(x)\right ]_{1}^{\text{e}} \\ & = H(\text{e})-H(1) \\ & = 6\text{e}\ln \text{e} - \dfrac{3}{2}\text{e}^2 - 2\text{e}-\left ( 6 \ln 1 - \dfrac{3}{2} - 2\right )\\ & = - \dfrac{3}{2}\text{e}^2 +4\text{e} + \dfrac{7}{2}\\ \end{array}$$
$$I = \displaystyle\int_{1}^{\text{e}}f(x)\:\text{d}x = - \dfrac{3}{2}\text{e}^2 +4\text{e} + \dfrac{7}{2} $$
3. Donner une interprétation graphique du nombre $I$.

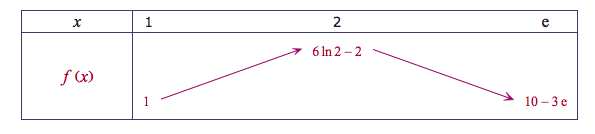
Les variations de la fonction $f$ sur l'intervalle $[1;\text{e}]$ sont :


Sur l'intervalle 1e la fonction $f$ est positive donc l'intégrale $I = \displaystyle\int_{1}^{\text{e}}f(x)\:\text{d}x = - \dfrac{3}{2}\text{e}^2 +4\text{e} + \dfrac{7}{2} $ est l'aire, exprimée en unités d'aire, du domaine compris entre la courbe $\mathcal{C}_{f}$, l'axe des abscisses et les droites d'équation $x=1$ et $x=\text{e}$.
4. 1. l'aide du graphique, donner la valeur de $F(1)$.
   
   
   La courbe $\Omega$ passe par le point de coordonnées $(1;-8 )$ donc $F(⁡1)=-8$
   2. En déduire une expression de $F(x)$ pour tout $x$ dans l'intervalle $]0; + \infty[$.
   
   $H$ et $F$ sont deux primitives de la fonction $f $donc pour tout réel $x$ strictement positif, $F(x)=H(x)+C$ où, $C$ est un nombre réel. Comme $F(1)=-8$ alors, $H(1)+C=-8\iff - \dfrac{3}{2}-2+C =-8\iff C =- \dfrac{9}{2}$
   $F$ est la fonction définie sur $]0~;~ + \infty[$ par $F(x)= 6x\ln x - \dfrac{3}{2}x^2 - 2x -\dfrac{9}{2}$