Baccalauréat Polynésie 11 septembre 2014 STI2D--STL spécialité SPCL
Exercice 1 4 points
On considère les nombres complexes $Z_{1}$ et $Z_{2}$ : \[Z_{1} = \dfrac{3\sqrt{2}}{1 + \text{i}}\quad \text{et}\quad Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}}.\]
- Ecrire les nombres $Z_{1}$ et $Z_{2}$ sous forme algébrique et trigonométrique.
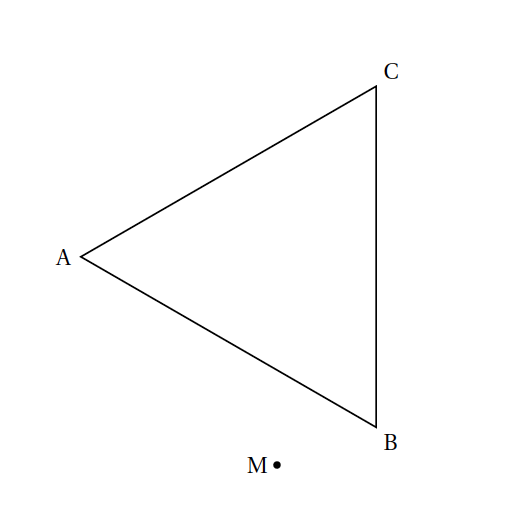
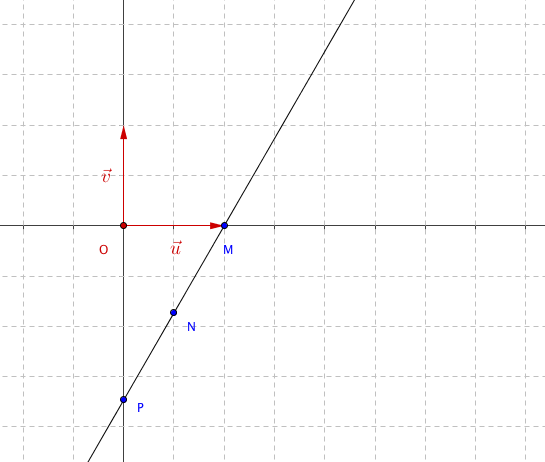
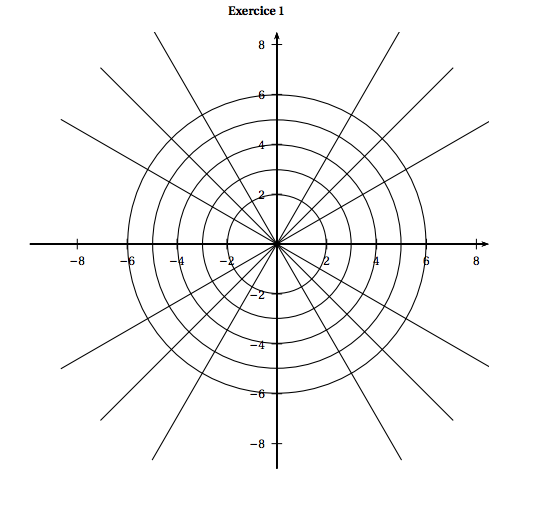
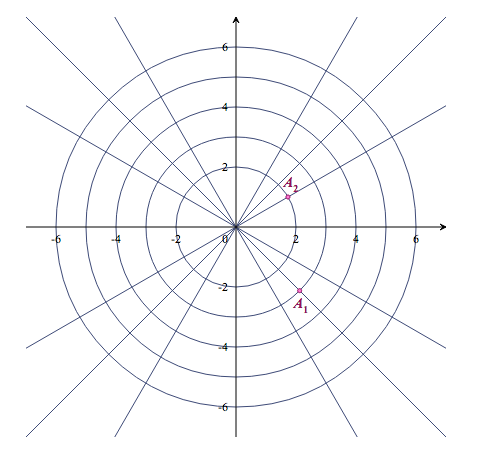
- Placer les points A$_{1}$ et A$_{2}$ d'affixes respectives $Z_{1}$ et $Z_{2}$ dans le repère donné en annexe.
- Calculer sous forme algébrique le produit $Z_{1} \times Z_{2}$ et donner sa forme trigonométrique.
- En déduire les valeurs exactes de $\cos \dfrac{\pi}{12}$ et $\sin \dfrac{\pi}{12}$.
Correction de l'exercice 1 (4 points)
On considère les nombres complexes $Z_{1}$ et $Z_{2}$ : \[Z_{1} = \dfrac{3\sqrt{2}}{1 + \text{i}}\quad \text{et}\quad Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}}.\]
- Ecrire les nombres $Z_{1}$ et $Z_{2}$ sous forme algébrique et trigonométrique.
- Forme algébrique de $Z_1$ $$\begin{array}{ll} Z_{1} &= \dfrac{3\sqrt{2}}{1 + \text{i}} \\ & = \dfrac{3\sqrt{2}(1 - \text{i})}{(1 + \text{i})(1 - \text{i})}\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{ 1^2+1^2 }\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }\\ \end{array}$$
- Forme trigonométrique de $Z_1$ Forme trigonométrique de $ Z_1= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }=\dfrac{3\sqrt{2}}{2} -\text{i} \dfrac{3\sqrt{2}}{2}$:
- Forme algébrique de $Z_2$ $$\begin{array}{ll} Z_{2} &= Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}} \\ & = \dfrac{4\text{i}(1 - \text{i}\sqrt{3})}{(1 + \text{i}\sqrt{3})(1 - \text{i}\sqrt{3})}\\ & = \dfrac{4\text{i} + 4 \sqrt{3}}{ 1^2+\sqrt 3^2 }\\ & = \dfrac{4 \sqrt{3} 4\text{i}}{4 }\\\end{array}$$
- Forme trigonométrique de $Z_2$ Forme trigonométrique de $Z_2=\sqrt{3} +\text{i}$:
$ Z_1= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }$.
Module : $|Z_1|=\sqrt{a^2+b^2}=\sqrt{\left(\dfrac{3\sqrt{2}}{2}\right)^2+\left(\dfrac{3\sqrt{2}}{2}\right)^2}=\sqrt{\dfrac{18}{4}+\dfrac{18}{4}}= \sqrt{9}=3$
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{\dfrac{3\sqrt{2}}{2}}{3}= \dfrac{\sqrt 2}{2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{\dfrac{-3\sqrt{2}}{2}}{3}= -\dfrac{\sqrt 2}{2} \end{array} \right.$$ Ainsi $\theta=-\dfrac{\pi}{4}$ convient; on a donc: $$Z_1=[3;-\dfrac{\pi}{4}] \text{ ou } Z_1=3\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$La forme exponentielle de $Z_{1}$ est $Z_1= 3e^{-i\frac{\pi}{4}}$
La forme trigonométrique de $Z_1$ est $Z_1=3\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$ Z_2= \sqrt{3} +\text{i}$.
Module : $|Z_2|=\sqrt{a^2+b^2}=\sqrt{\sqrt{3}^2+1^2}=\sqrt{4}=2$
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{\sqrt{3}}{2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{1}{2} \end{array} \right.$$ Ainsi $\theta= \dfrac{\pi}{6}$ convient; on a donc: $$Z_2=[2; \dfrac{\pi}{6}] \text{ ou } Z_2=2\left [\cos\left (\dfrac{\pi}{6}\right )+i\sin\left (\dfrac{\pi}{6}\right )\right ]$$La forme exponentielle de $Z_{2}$ est $Z_2= 2e^{i\frac{\pi}{6}}$
La forme trigonométrique de $Z_2$ est $Z_2=2\left [\cos\left (\dfrac{\pi}{6}\right )+i\sin\left (\dfrac{\pi}{6}\right )\right ]$ - Placer les points A$_{1}$ et A$_{2}$ d'affixes respectives $Z_{1}$ et $Z_{2}$ dans le repère donné en annexe.
- Calculer sous forme algébrique le produit $Z_{1} \times Z_{2}$ et donner sa forme trigonométrique.
- Forme algébrique de $Z_1\times Z_2$ $$\begin{array}{ll} Z_{1}\times Z_2 &= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }\times ( \sqrt{3} +\text{i}) \\ & = \dfrac{3\sqrt{6}}{2} +\text{i} \dfrac{3\sqrt{2}}{2}- \text{i} \dfrac{3\sqrt{6}}{2} +\dfrac{3\sqrt{2}}{2}\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{ 1^2+1^2 }\\ & = \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2}\\\end{array}$$
- Forme trigonométrique de $Z_1\times Z_2$ $$\begin{array}{ll} Z_{1}\times Z_2 &= 3e^{-i\frac{\pi}{4}} \times 2e^{i\frac{\pi}{6}} \\ & = 6 e^{i\left(-\frac{\pi}{4} + \frac{\pi}{6}\right)} \\ & = 6 e^{-i\frac{\pi}{12} } \\\\\end{array}$$
$ Z_1\times Z_2 = \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2}$.La forme trigonométrique de $ Z_1\times Z_2$ est $ Z_1\times Z_2 = 6 e^{-i\frac{\pi}{12} }$ - En déduire les valeurs exactes de $\cos \dfrac{\pi}{12}$ et $\sin \dfrac{\pi}{12}$. On identifie les formes algébrique et trigonométrique de $ Z_1\times Z_2$: $$ Z_1\times Z_2 = 6 e^{-i\frac{\pi}{12} }=6\left [\cos\left (\dfrac{-\pi}{12}\right )+i\sin\left (\dfrac{-\pi}{12}\right )\right ]$$ $$\begin{array}{ll } Z_1\times Z_2&= \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2} \\ &= 6\left [\cos\left (\dfrac{-\pi}{12}\right )+i\sin\left (\dfrac{-\pi}{12}\right )\right ] \end{array}$$ En identifiant les parties réelles et les parties imaginaires on obtient : $$\left\{ \begin{array}{l } Re(Z_1\times Z_2 )=6\cos(\dfrac{-\pi}{12})= 6\cos(\dfrac{\pi}{12})=\dfrac{3(\sqrt{6}+\sqrt{2})}{2} \\ Im(Z_1\times Z_2 )=6\sin(-\dfrac{\pi}{12})=-6\sin(\dfrac{\pi}{12})= \dfrac{3(\sqrt{2}-\sqrt{6})}{2} \end{array} \right.$$
Exercice 2 6 points
Une entreprise informatique a réalisé en 2013 un bénéfice de 22000 €. La direction de cette entreprise se fixe pour objectif une hausse annuelle de son bénéfice de 4,5$\,\%$. Pour tout entier naturel $n$, on note $b_{n}$ le bénéfice prévu pour l'année $2013 + n$, on a donc $b_{0} = 22000$.
Partie A
- Calculer les bénéfices $b_{1}$ et $b_{2}$ espérés pour 2014 et 2015.
- Montrer que $\left(b_{n}\right)$ est une suite géométrique dont on précisera les éléments caractéristiques.
- Exprimer alors $b_{n}$ en fonction de $n$.
Partie B
On considère l'algorithme ci-dessous :
$$\begin{array}{|l|}\hline N \text{ prend la valeur } 0\\ B \text{ prend la valeur }22000 \\ \text{ Tant que } B \leqslant 40000 \\ \hspace{0,5cm}N \text{ prend la valeur } N + 1\\ \hspace{0,5cm}B \text{ prend la valeur }1,045 * B\\ \text{ Fin Tant que } \\ A \text{ prend la valeur } N + 2013\\ \text{ Afficher } A\\ \hline \end{array}$$
- Expliquer à quoi correspondent les variables N et B.
- Exécuter cet algorithme et donner le dernier résultat affiché.
- Expliquer à quoi correspond cette valeur. La direction souhaite savoir à partir de quelle année le bénéfice de l'entreprise sera supérieur à 40000 €.
- Résoudre dans $\mathbb R$ l'inéquation suivante: \[22000 \times 1,045^x > 40000.\]
- Quel lien existe-t-il entre le résultat de la question 2. de la partie B et l'ensemble des solutions de l'inéquation précédente ?
Correction de l'exercice 2 (6 points)
Une entreprise informatique a réalisé en 2013 un bénéfice de 22000 €. La direction de cette entreprise se fixe pour objectif une hausse annuelle de son bénéfice de 4,5$\,\%$. Pour tout entier naturel $n$, on note $b_{n}$ le bénéfice prévu pour l'année $2013 + n$, on a donc $b_{0} = 22000$.
Partie A
- Calculer les bénéfices $b_{1}$ et $b_{2}$ espérés pour 2014 et 2015. $b_1=22000\times \left(1+\dfrac{4,5}{100}\right)=22990$ $b_2=22990\times \left(1+\dfrac{4,5}{100}\right)= 24024,55$
- Montrer que $\left(b_{n}\right)$ est une suite géométrique dont on précisera les éléments caractéristiques. $b_0=22000$ et, pour tout entier naturel $n, b_{n+1}=1,045\times b_n$
- Exprimer alors $b_{n}$ en fonction de $n$. $(b_n)$ est une suite géométrique de raison $1,045$ et de premier terme $22000$, $b-n=q^n\times b-0$
Partie B
On considère l'algorithme ci-dessous :$$\begin{array}{|l|}\hline N \text{ prend la valeur } 0\\ B \text{ prend la valeur }22000 \\ \text{ Tant que } B \leqslant 40000 \\ \hspace{0,5cm}N \text{ prend la valeur } N + 1\\ \hspace{0,5cm}B \text{ prend la valeur }1,045 * B\\ \text{ Fin Tant que } \\ A \text{ prend la valeur } N + 2013\\ \text{ Afficher } A\\ \hline \end{array}$$
- Expliquer à quoi correspondent les variables N et B.
- Exécuter cet algorithme et donner le dernier résultat affiché.
- Expliquer à quoi correspond cette valeur.
- Résoudre dans $\mathbb R$ l'inéquation suivante: \[22000 \times 1,045^x > 40000.\] Pour tout réel $x$, on a $$\begin{array}{ll} 22000 \times 1,045^x > 40000 &\iff 1,045^x > \dfrac{40000}{22 000}\\ &\iff e^{x \ln(1,045)} > \dfrac{20}{11}\\ &\iff \ln\left(e^{x \ln(1,045)} \right)> \ln\left(\dfrac{20}{11}\right)\\ &\iff x \ln(1,045) > \ln\left(\dfrac{20}{11}\right)\\ &\iff x > \dfrac{\ln\left(\dfrac{20}{11}\right)}{\ln(1,045)}\\ \end{array}$$
- Quel lien existe-t-il entre le résultat de la question 2. de la partie B et l'ensemble des solutions de l'inéquation précédente ?
Exercice 3 6 points
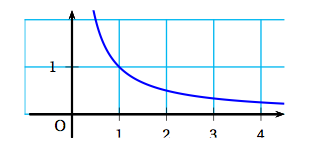
Lorsque l'on consomme de l'alcool, le taux d'alcool dans le sang varie en fonction du temps écoulé depuis l'absorption. Ce taux est appelé « alcoolémie » et est mesuré en grammes par litre (g/L). Après l'absorption de trois verres d'alcool, l'alcoolémie d'une personne donnée, en fonction du temps (exprimé en heures), est modélisée par la fonction définie sur $\mathbb R_{+}$ par : \[ f(t) = 2,5t\text{e}^{- t}.\]
Partie A
- Donner la valeur de l'alcoolémie de la personne considérée au bout de 2 heures.
- Montrer que pour tout réel $t$ de l'intervalle $[0~;~+ \infty[$, $f'(t) = 2,5(1 - t)\text{e}^{- t}$.
- Vérifier que la fonction $f$ est solution de l'équation différentielle : \[(E) :\qquad y' + y = 2,5\text{e}^{- t}.\]
- En remarquant que pour tout réel $t$ de l'intervalle $[0~;~+ \infty[$ on a $f(t) = \dfrac{2,5t}{\text{e}^{t}}$, déterminer $\displaystyle\lim_{t \to + \infty}f(t)$ et donner une interprétation géométrique de cette limite.
- Déterminer les variations de la fonction $f$ sur l'intervalle $[0~;~+ \infty[$.
- Quelle est l'alcoolémie la plus élevée pour la personne considérée ?
Partie B
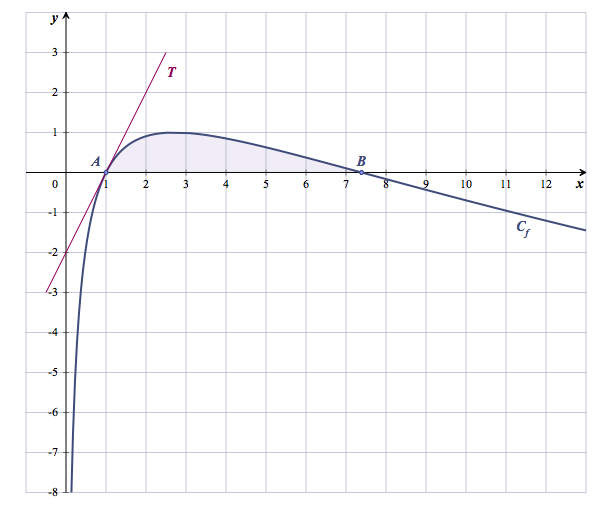
- Sur une feuille de papier millimétré, tracer la courbe représentative de la fonction $f$ sur l'intervalle $[0~;~+ \infty[$. On prendra 2 cm pour unité sur l'axe des abscisses et 10 cm pour unité sur l'axe des ordonnées.
- En France, la législation autorise pour un conducteur une alcoolémie maximale de 0,5 g/L. Sachant que la personne a absorbé trois verres d'alcool à 12 h, à partir de quelle heure pourra-t-elle reprendre la route pour effectuer sans s'arrêter un trajet d'une durée d'une heure ? On utilisera la représentation graphique de la fonction $f$.
Correction de l'exercice 3 (6 points)
Lorsque l'on consomme de l'alcool, le taux d'alcool dans le sang varie en fonction du temps écoulé depuis l'absorption. Ce taux est appelé « alcoolémie » et est mesuré en grammes par litre (g/L). Après l'absorption de trois verres d'alcool, l'alcoolémie d'une personne donnée, en fonction du temps (exprimé en heures), est modélisée par la fonction définie sur $\mathbb R_{+}$ par : \[ f(t) = 2,5t\text{e}^{- t}.\]
Partie A
- Donner la valeur de l'alcoolémie de la personne considérée au bout de 2 heures. $f(2)=2,5\times 2\times e{-2}\approx 0,68$
- Montrer que pour tout réel $t$ de l'intervalle $[0~;~+ \infty[$, $f'(t) = 2,5(1 - t)\text{e}^{- t}$.
- Vérifier que la fonction $f$ est solution de l'équation différentielle : \[(E) :\qquad y' + y = 2,5\text{e}^{- t}.\] $$\begin{array}{ll} f’(t)+f(t)&=2,5(1−t)\text{e}^{-t}+2,5t\text{e}^{-t}\\ &= 2,5 \text{e}^{- t} \end{array}$$
- En remarquant que pour tout réel $t$ de l'intervalle $[0~;~+ \infty[$ on a $f(t) = \dfrac{2,5t}{\text{e}^{t}}$, déterminer $\displaystyle\lim_{t \to + \infty}f(t)$ et donner une interprétation géométrique de cette limite. $\displaystyle\lim_{t \to + \infty}\dfrac{\text{e}^{t}}{t}=+\infty$, donc par inverse : $\displaystyle\lim_{t \to + \infty}\dfrac{t}{\text{e}^{t}}=0$, puis $\displaystyle\lim_{t \to + \infty}\dfrac{2,5t}{\text{e}^{t}}=0$
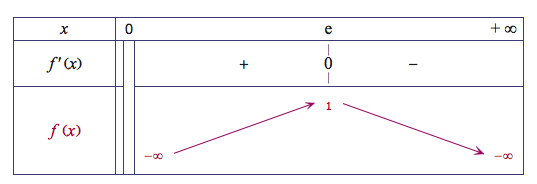
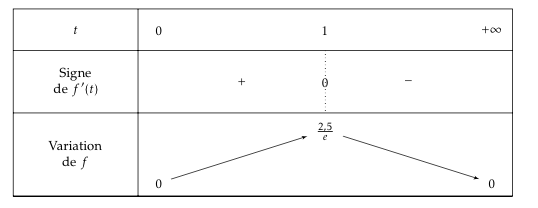
- Déterminer les variations de la fonction $f$ sur l'intervalle $[0~;~+ \infty[$. Le sens de variation de $f$ est donné par le signe de la dérivée $f’$; or $f’(t)=2,5(1-t)\text{e}^{-t}$
- Quelle est l'alcoolémie la plus élevée pour la personne considérée ? Le maximum de la fonction $f$ est atteint pour $t=1$ et, $$f(1)=2,5\times \text{e}^{-1}\approx 0,92$$
$f $ est dérivable comme produit de deux fonctions dérivables :
$f=uv$ d'où $f'=u' v+uv' $ avec pour tout réel $x$ :
$$\left\{ \begin{array}{l} u(t)~ =2,5t \\ v(t)~ =\text{e}^{- t} \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u’(t)~ =2,5 \\ v'(t)~ =-\text{e}^{- t} \end{array}\right.$$
Ainsi :
$$f’(t)=2,5 \times \text{e}^{- t} +2,5t \times \left( -\text{e}^{- t}\right)$$
Comme la fonction exponentielle est strictement positive sur $\mathbb{R}$ ; le signe de $f′(t)$ ne dépend que de celui de $1-t$. On obtient donc le tableau de variations suivant :
Partie B
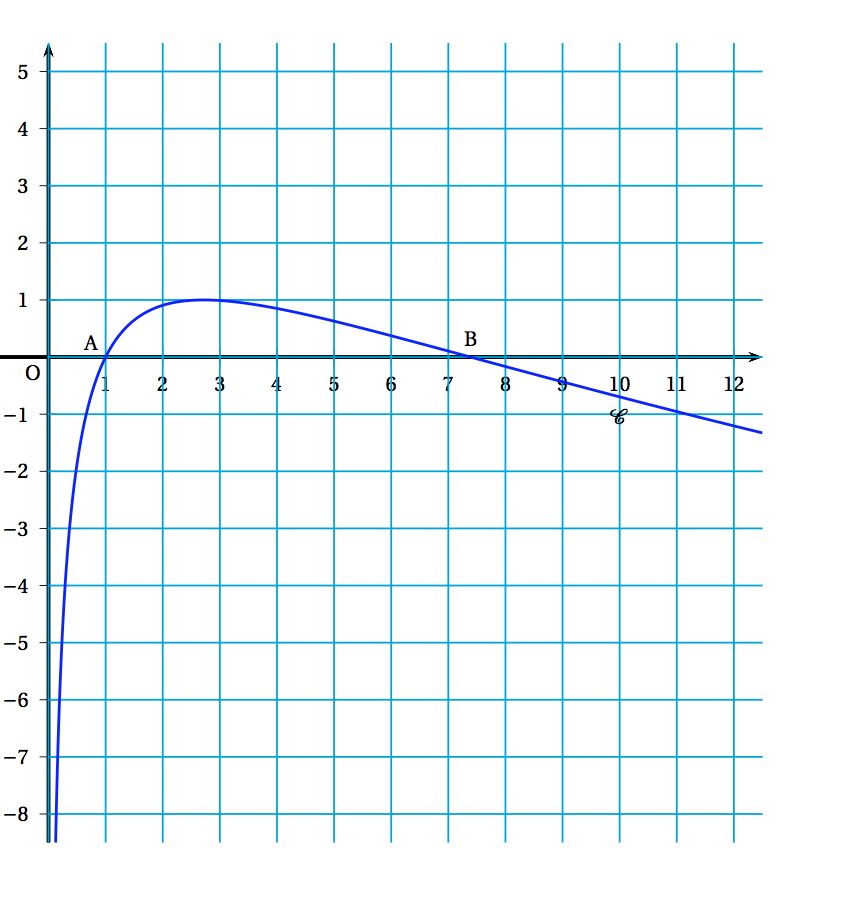
- Sur une feuille de papier millimétré, tracer la courbe représentative de la fonction $f$ sur l'intervalle $[0~;~+ \infty[$. On prendra 2 cm pour unité sur l'axe des abscisses et 10 cm pour unité sur l'axe des ordonnées.
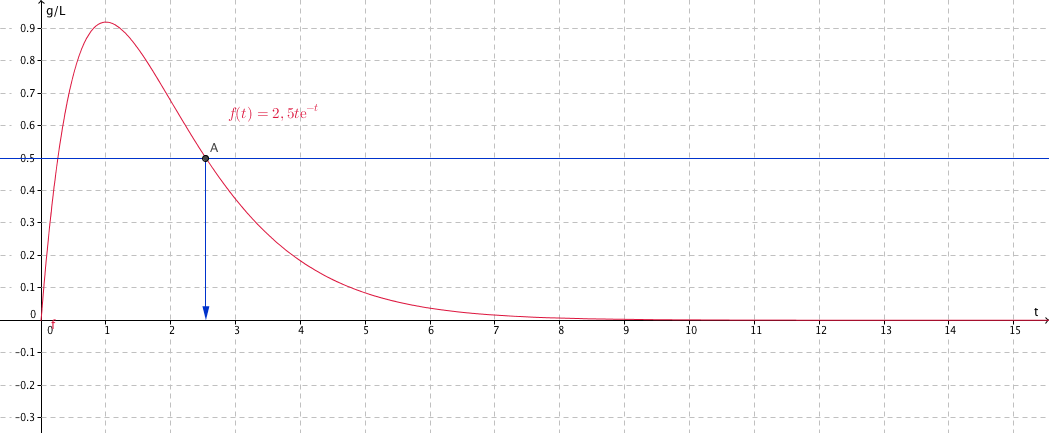
- En France, la législation autorise pour un conducteur une alcoolémie maximale de 0,5 g/L. Sachant que la personne a absorbé trois verres d'alcool à 12 h, à partir de quelle heure pourra-t-elle reprendre la route pour effectuer sans s'arrêter un trajet d'une durée d'une heure ? On utilisera la représentation graphique de la fonction $f$. Avec la précision permise par un graphique tracé à main levée, on constate que la courbe représentative de la fonction $f$ est en dessous de la droite d'équation $y=0,5$ sur un intervalle d'amplitude 1 pour $t>2,5$. Or $f(2,5)\approx 0,513$ et $f(2,55)\approx 0,498$
Exercice 4 4 points
Partie A Loi exponentielle et radioactivité
On modélise la durée de vie $T$ (exprimée en jours) d'un élément radioactif par une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$.
On rappelle que pour tout $t > 0,\: P(T \leqslant t) = \displaystyle\int_{0}^t \lambda\text{e}^{- \lambda x}\:\text{d}x$.
Le Thorium 227 a une demi-vie de 18 jours, ce qui signifie que : \[P(T \geqslant 18) = P(T \leqslant 18) = 0,5.\]
- Montrer que pour tout $t > 0,\: P(T \leqslant t) = 1 - \text{e}^{-\lambda t}$.
- Calculer la valeur du paramètre $\lambda$ pour le Thorium 227. On donnera le résultat arrondi à $10^{-4}$.
- On suppose que $\lambda = 0,04$. Donner alors la durée de vie moyenne d'un atome de Thorium 227.
Partie B Loi normale et usinage
Une entreprise fabrique en grande quantité des pièces tubulaires destinées à l'industrie aérospatiale. Le diamètre (exprimé en centimètres) d'une de ces pièces est modélisé par une variable aléatoire $X$ suivant la loi normale d'espérance $3,65$ et d'écart type $0,004$.
Les résultats seront donnés à $10^{-3}$ près .
- Une pièce est décrétée conforme lorsque son diamètre en centimètres est compris entre $3,645$ et $3,655$. Calculer la probabilité qu'une pièce tubulaire de la production soit décrétée conforme.
- Dans le cadre d'un fonctionnement correct de la chaîne de production, on admet que la proportion $p$ de pièces conformes est 79$\,\%$. On rappelle que l'intervalle de fluctuation asymptotique à 95$\,\%$ de la fréquence de pièces conformes sur un échantillon de taille $n$ est \[I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{n}}\right].\] On contrôle régulièrement la chaîne de production en prélevant des échantillons de $100$ pièces. Lors d'un contrôle, on trouve 25 pièces défectueuses. Le responsable qualité doit-il prendre la décision d'effectuer des réglages sur la chaîne de production ? Justifier la réponse.
Exercice 4 : 4 points
Partie A Loi exponentielle et radioactivité
On modélise la durée de vie $T$ (exprimée en jours) d'un élément radioactif par une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$.
On rappelle que pour tout $t > 0,\: P(T \leqslant t) = \displaystyle\int_{0}^t \lambda\text{e}^{- \lambda x}\:\text{d}x$.
Le Thorium 227 a une demi-vie de 18 jours, ce qui signifie que : \[P(T \geqslant 18) = P(T \leqslant 18) = 0,5.\]
- Montrer que pour tout $t > 0,\: P(T \leqslant t) = 1 - \text{e}^{-\lambda t}$. $$\begin{array}{ll} P(T \leqslant t)& = \displaystyle\int_{0}^t \lambda\text{e}^{- \lambda x}\:\text{d}x\\ &=\left[ -\text{e}^{- \lambda x}\right]_0^t\\ &= -\text{e}^{- \lambda t}-(-\text{e}^{0})\\ & 1 -\text{e}^{- \lambda t}\\ \end{array}$$
- Calculer la valeur du paramètre $\lambda$ pour le Thorium 227. On donnera le résultat arrondi à $10^{-4}$. $$\begin{array}{ll} 1 -\text{e}^{- 18\lambda } =0,5&\iff \text{e}^{- 18\lambda } =0,5 \\ &\iff \ln\left(\text{e}^{- 18\lambda } \right)=\ln (0,5)\\ &\iff - 18\lambda= \ln (0,5)\\ &\iff \lambda = -\dfrac{\ln (0,5)}{18}\approx 0,0385 \end{array}$$
- On suppose que $\lambda = 0,04$. Donner alors la durée de vie moyenne d'un atome de Thorium 227. L'espérance d'une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$ est égale à $\dfrac{1}{\lambda}$.
Partie B Loi normale et usinage
Une entreprise fabrique en grande quantité des pièces tubulaires destinées à l'industrie aérospatiale. Le diamètre (exprimé en centimètres) d'une de ces pièces est modélisé par une variable aléatoire $X$ suivant la loi normale d'espérance $3,65$ et d'écart type $0,004$.
Les résultats seront donnés à $10^{-3}$ près .
- Une pièce est décrétée conforme lorsque son diamètre en centimètres est compris entre $3,645$ et $3,655$. Calculer la probabilité qu'une pièce tubulaire de la production soit décrétée conforme.
- Dans le cadre d'un fonctionnement correct de la chaîne de production, on admet que la proportion $p$ de pièces conformes est 79$\,\%$. On rappelle que l'intervalle de fluctuation asymptotique à 95$\,\%$ de la fréquence de pièces conformes sur un échantillon de taille $n$ est \[I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{n}}\right].\] On contrôle régulièrement la chaîne de production en prélevant des échantillons de $100$ pièces. Lors d'un contrôle, on trouve 25 pièces défectueuses. Le responsable qualité doit-il prendre la décision d'effectuer des réglages sur la chaîne de production ? Justifier la réponse.
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
La fréquence observée de pièces conformes dans l'échantillon est $f=\dfrac{100-25}{100}≈0,75$
- Vues: 22074