Baccalauréat STI 2D/STL spécialité SPCL Nouvelle-Calédonie 27 novembre 2018
Exercice 1 5 points
Les trois parties de cet exercice peuvent être traitées de façon indépendante.
Les organismes vivants contiennent naturellement du carbone 14 (élément radioactif) provenant des rayons cosmiques, qui est constamment renouvelé et qui se maintient à la valeur de 15,3 unités. À leur mort, l'assimilation cesse et le carbone 14 présent se désintègre.
On note $f(t)$ la concentration en carbone 14 présent dans un organisme à l'instant $t$ après sa mort (t exprimé en milliers d'années).
Partie A
On admet que $f$ est une solution sur $[0~;~+\infty[$ de l'équation différentielle : \[ y' = - 0,124y \qquad (E).\]
- Résoudre l'équation différentielle $(E)$.
- Déterminer la solution $f$ de $(E)$ vérifiant la condition initiale $f(0) = 15,3$.
Partie B
On admet que la fonction $f$ est définie par $f(t) = 15,3\text{e}^{-0,124t}$ sur $[0~;~+\infty[$.
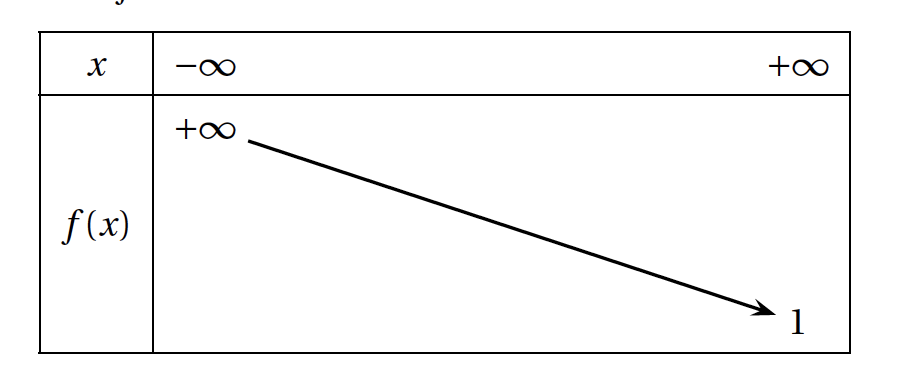
- Déterminer les variations de $f$ sur $[0~;~+\infty[$.
- Déterminer la limite de $f$ au voisinage de l'infini. Interpréter ce résultat dans le contexte de l'énoncé.
Partie C
On rappelle que la fonction $f$ donnée dans la partie B donne la concentration en carbone 14 dans un organisme après sa mort en fonction de $t$ (en milliers d'années).
- Des archéologues ont trouvé des fragments d'os présentant une concentration en carbone 14 égale à $7,27$ unités. Justifier que l'on peut estimer l'âge de ces fragments d'os à 6000 ans.
- Lorsque la concentration en carbone 14 d'un organisme devient inférieure à $0,3$ % de sa valeur initiale on ne peut pas dater raisonnablement à l'aide du carbone 14. Déterminer l'âge à partir duquel un organisme ne peut plus être daté au carbone 14.
Correction de l'exercice 1 (5 points)
Les trois parties de cet exercice peuvent être traitées de façon indépendante.
Les organismes vivants contiennent naturellement du carbone 14 (élément radioactif) provenant des rayons cosmiques, qui est constamment renouvelé et qui se maintient à la valeur de 15,3 unités. À leur mort, l'assimilation cesse et le carbone 14 présent se désintègre.
On note $f(t)$ la concentration en carbone 14 présent dans un organisme à l'instant $t$ après sa mort (t exprimé en milliers d'années).
Partie A
On admet que $f$ est une solution sur $[0~;~+\infty[$ de l'équation différentielle : \[ y' = - 0,124y \qquad (E).\]
- Résoudre l'équation différentielle $(E)$. L'équation différentielle $y'=-0,124 y$ est de la forme $y'=ay$ avec $a=-0,124$.
- Déterminer la solution $f$ de $(E)$ vérifiant la condition initiale $f(0) = 15,3$. $f(0)=15,3$ équivaut à $k\text{e}^0=15,3$ soit $k=15,3$
Les solutions de cette équation différentielle sont les fonctions $f$ définies sur $\mathbb{R}$ par $f(t)= k\text{e}^{-0,124 t}$, où $k$ est une constante réelle quelconque.
Par conséquent, les solutions sur $[0;+\infty[$ de l'équation différentielle (E) sont les fonctions définies pour tout réel $t$ positif par $f(t)= k\text{e}^{-0,124 t}$ où k est une constante réelle quelconque.
La solution de l'équation différentielle (E) vérifiant la condition initiale $f(0)=15,3$ est la fonction $f$ définie sur $[0;+\infty[$ par $f(t)= 15,3\text{e}^{-0,124 t}$
Partie B
On admet que la fonction $f$ est définie par $f(t) = 15,3\text{e}^{-0,124t}$ sur $[0~;~+\infty[$.
- Déterminer les variations de $f$ sur $[0~;~+\infty[$. La dérivée de la fonction $f$ est la fonction $f'$ définie sur $[0;+\infty[$ par :$f'(t)= 15,3\times (-0,124)e^{-0,124 t}= -1,8972e^{-0,124 t}$.
- Déterminer la limite de $f$ au voisinage de l'infini. Interpréter ce résultat dans le contexte de l'énoncé. $\left.\begin{array}{l} \lim\limits_{t \to +\infty}~(-0,124 t)=-\infty \\ \lim\limits_{X \to -\infty}~ \text{e} ^X=0 \end{array}\right\}\; \text{ par composée }\lim\limits_{t \to +\infty}~ \text{e} ^{-0,124t}=0 $ Ainsi $\lim\limits_{t \to +\infty}~15,3 \text{e} ^{-0,124t}=0$ , et donc $\lim\limits_{t \to +\infty}~f(t)=0$.
Comme pour tout réel $t$ on a $e^{-0,124 t}> 0$,par ailleurs $-0,124<0$ on en déduit que sur l'intervalle $[0;+\infty[$ $-1,8972e^{-0,124 t}<0$.
Sur l'intervalle $[0;+\infty[$, on a $f'(t)<0$ donc la fonction $f$ est strictement décroissante.
La concentration en carbone 14 présent dans un organisme sera proche de 0 à partir d'un certain nombre de milliers d'années après sa mort .
Partie C
On rappelle que la fonction $f$ donnée dans la partie B donne la concentration en carbone 14 dans un organisme après sa mort en fonction de $t$ (en milliers d'années).
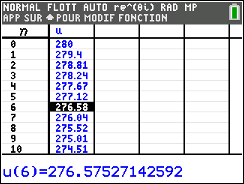
- Des archéologues ont trouvé des fragments d'os présentant une concentration en carbone 14 égale à $7,27$ unités. Justifier que l'on peut estimer l'âge de ces fragments d'os à 6000 ans. $$\begin{array}{rl} 15,3 \text{e} ^{-0,124t}=7,27&\iff \text{e} ^{-0,124t}=\dfrac{7,27}{15,3}\\ & \iff \ln\left ( \text{e} ^{-0,124t} \right )= \ln\left ( \dfrac{7,27}{15,3} \right )\\ & \iff -0,124t = \ln\left ( \dfrac{7,27}{15,3} \right )\\ &\iff t= \dfrac{\ln\left ( \dfrac{7,27}{15,3} \right )}{-0,124} \end{array}$$ $\dfrac{\ln\left ( \dfrac{7,27}{15,3} \right )}{-0,124}\approx 6$
- Lorsque la concentration en carbone 14 d'un organisme devient inférieure à $0,3$ % de sa valeur initiale on ne peut pas dater raisonnablement à l'aide du carbone 14. Déterminer l'âge à partir duquel un organisme ne peut plus être daté au carbone 14. $$\begin{array}{rl} 15,3 \text{e} ^{-0,124t} < 15,3\times 0,003&\iff \text{e} ^{-0,124t}< 0,003\\ & \iff \ln\left ( \text{e} ^{-0,124t} \right )< \ln\left ( 0,003 \right )\\ & \iff -0,124t < \ln\left ( 0,003 \right )\\ &\iff t> \dfrac{\ln\left (0,003 \right )}{-0,124} \end{array}$$ $\dfrac{\ln\left ( 0,003 \right )}{-0,124}\approx 46,8$
Ainsi, on peut estimer l'âge de ces fragments d'os à 6 000 ans.
Un organisme ne peut plus être daté au carbone 14 au bout 47 000 ans.
Exercice 2 5 points
Les trois parties de cet exercice peuvent être traitées de façon indépendante. Dans cet exercice, les résultats seront arrondis au millième.
La société Héliocel fabrique des cellules photovoltaïques destinées à être assemblées pour former des panneaux solaires qui seront ensuite installés sur le toit d'habitations pour produire de l'électricité.
Partie A
On estime que 5 % des cellules fabriquées par Héliocel présentent un défaut et sont donc inutilisables.
On prélève au hasard un lot de $80$ cellules dans la production pour vérification. Le nombre de cellules produites est suffisamment important pour que l'on assimile ce prélèvement à un tirage avec remise de $80$ cellules. On appelle $X$ la variable aléatoire qui, à chaque lot de $80$ cellules, associe le nombre de cellules inutilisables.
- La variable aléatoire $X$ suit une loi binomiale. Préciser ses paramètres.
- Quelle est la probabilité qu'un lot ne contienne aucune cellule inutilisable ?
- Un panneau solaire est constitué de $75$ cellules. Quelle est la probabilité d'avoir assez de cellules sans défaut dans un seul lot pour pouvoir fabriquer un panneau ?
Partie B
Après amélioration sur sa chaîne de fabrication, la société annonce une proportion de 3 % de cellules inutilisables. Afin de vérifier cette annonce, le responsable qualité prélève de manière aléatoire un échantillon de $180$ cellules et observe que $9$ cellules sont inutilisables. Cette observation remet-elle en cause l'annonce de la société ?
Partie C
Une famille décide d'installer 15 de ces panneaux solaires sur le toit de sa maison pour produire de l'électricité. La production électrique dépend de l'ensoleillement. On appelle $Y$ la variable aléatoire qui, à chaque journée, associe la production électrique (en kWh) fournie par ces 15 panneaux. On admet que la variable aléatoire $Y$ suit la loi normale d'espérance $\mu = 9$ et d'écart-type $\sigma = 3$.
- Quelle est la probabilité que la production journalière de l'installation de cette famille soit comprise entre $6$ kWh et $12$ kWh ?
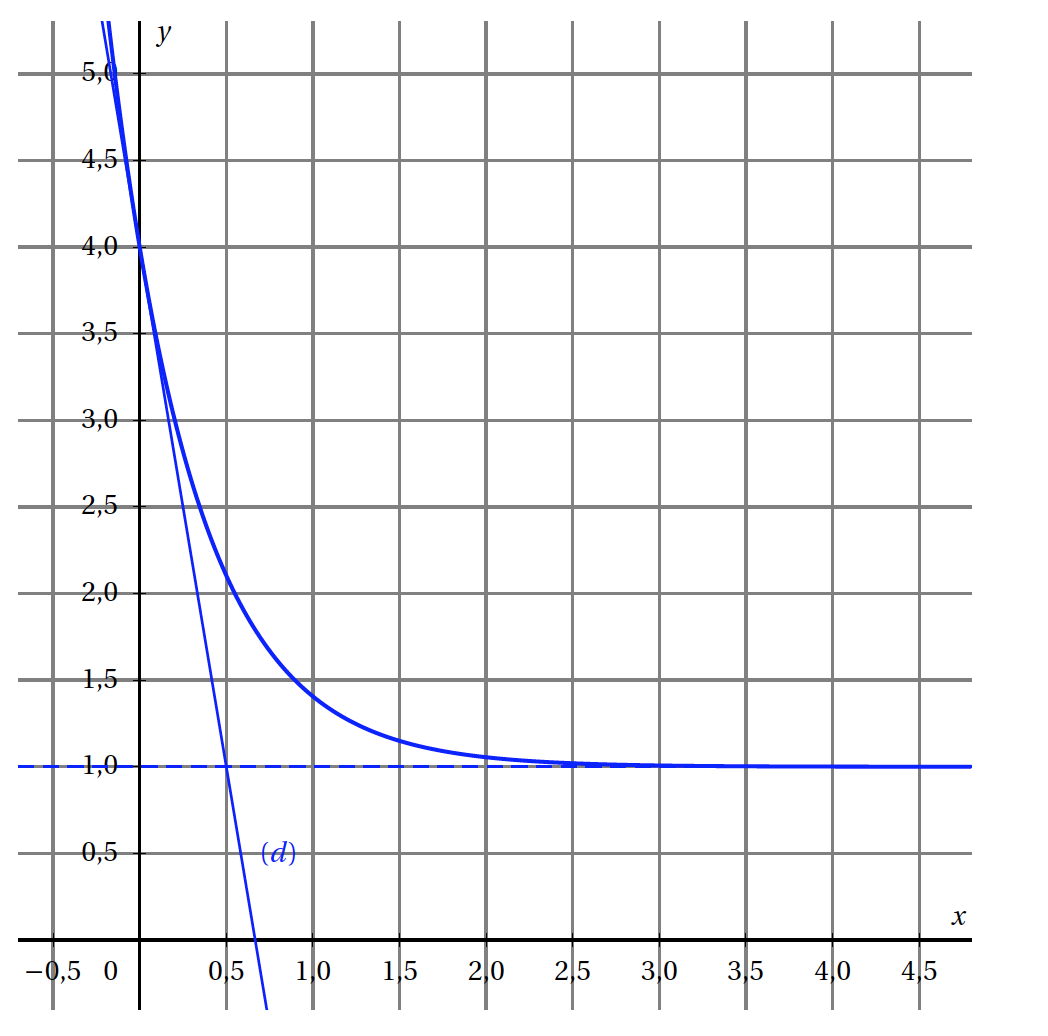
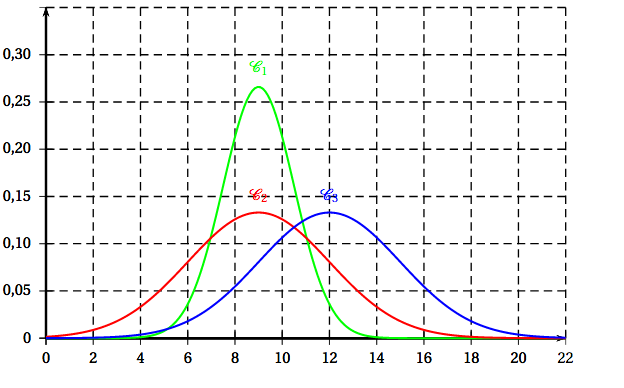
- Parmi les trois fonctions de densité de probabilité représentées ci-dessous, laquelle peut être celle de la loi de $Y$ ? Justifier.
- La consommation moyenne de cette famille est $13$ kWh/jour. Quelle est la probabilité que la production journalière de son installation soit supérieure à sa consommation moyenne quotidienne ?
Correction de l'exercice 2 (5 points)
Les trois parties de cet exercice peuvent être traitées de façon indépendante. Dans cet exercice, les résultats seront arrondis au millième.
La société Héliocel fabrique des cellules photovoltaïques destinées à être assemblées pour former des panneaux solaires qui seront ensuite installés sur le toit d'habitations pour produire de l'électricité.
Partie A
On estime que 5 % des cellules fabriquées par Héliocel présentent un défaut et sont donc inutilisables.
On prélève au hasard un lot de $80$ cellules dans la production pour vérification. Le nombre de cellules produites est suffisamment important pour que l'on assimile ce prélèvement à un tirage avec remise de $80$ cellules. On appelle $X$ la variable aléatoire qui, à chaque lot de $80$ cellules, associe le nombre de cellules inutilisables.
- La variable aléatoire $X$ suit une loi binomiale. Préciser ses paramètres. $X$ suit la loi binomiale de paramètres $n=80$ et $p=0,05$.
- Quelle est la probabilité qu'un lot ne contienne aucune cellule inutilisable ? $$P(X=0)=(1-0,05)^{80}\approx 0,017$$ Arrondie au millième près, la probabilité qu'un lot ne contienne aucune cellule inutilisable est 0,017.
- Un panneau solaire est constitué de $75$ cellules. Quelle est la probabilité d'avoir assez de cellules sans défaut dans un seul lot pour pouvoir fabriquer un panneau ? Dans un lot de 80 cellules, il y a au moins 75 cellules sans défaut si le nombre de cellules défectueuses est inférieur ou égal à 4. À la calculatrice, on obtient : $P(X\leq 4)\approx 0,629$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
Partie B
Après amélioration sur sa chaîne de fabrication, la société annonce une proportion de 3 % de cellules inutilisables. Afin de vérifier cette annonce, le responsable qualité prélève de manière aléatoire un échantillon de $180$ cellules et observe que $9$ cellules sont inutilisables. Cette observation remet-elle en cause l'annonce de la société ?
La fréquence observée des cellules inutilisables dans l'échantillon est $f=\dfrac{9}{180\times 75}=0,05$.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
$0,05\in [0,0050,055]$ donc l'hypothèse d'une proportion de 3 % de cellules inutilisables n'est pas remise en cause.
Partie C
Une famille décide d'installer 15 de ces panneaux solaires sur le toit de sa maison pour produire de l'électricité. La production électrique dépend de l'ensoleillement. On appelle $Y$ la variable aléatoire qui, à chaque journée, associe la production électrique (en kWh) fournie par ces 15 panneaux. On admet que la variable aléatoire $Y$ suit la loi normale d'espérance $\mu = 9$ et d'écart-type $\sigma = 3$.
- Quelle est la probabilité que la production journalière de l'installation de cette famille soit comprise entre $6$ kWh et $12$ kWh ? D'après le cours, si la variable aléatoire $Y$ suit la loi normale d'espérance $\mu$ et d'écart-type $\sigma$ alors $P(\mu-\sigma\leq Y\leq \mu+\sigma)\approx0,683$
- Parmi les trois fonctions de densité de probabilité représentées ci-dessous, laquelle peut être celle de la loi de $Y$ ? Justifier.
 Méthode 1 :
Méthode 1 : - La consommation moyenne de cette famille est $13$ kWh/jour. Quelle est la probabilité que la production journalière de son installation soit supérieure à sa consommation moyenne quotidienne ?
d'où $P(6\leq Y\leq 12)\approx 0,683$.
Ou un calcul direct donne :
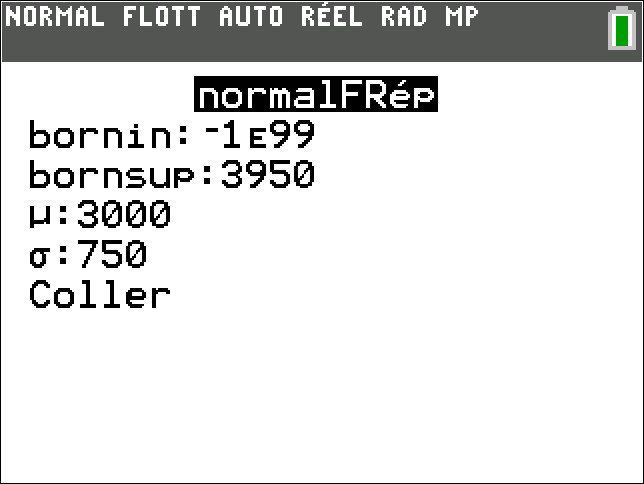
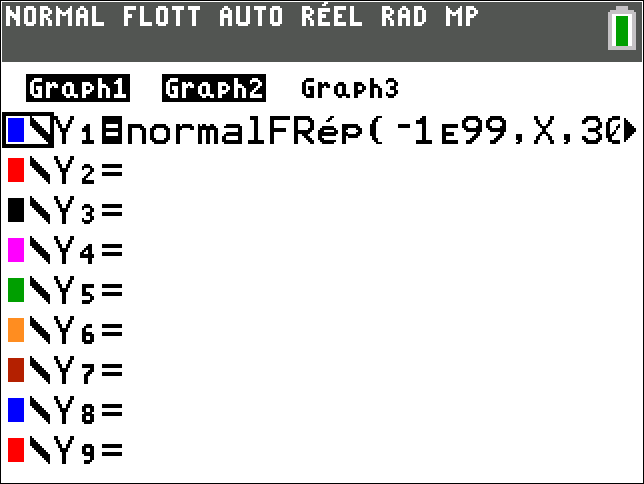
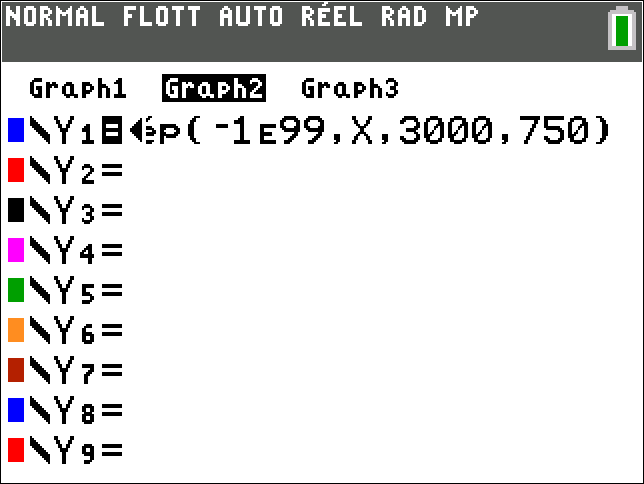
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Arrondie au millième près, la probabilité que la production journalière de l'installation de cette famille soit comprise entre 6 kWh et 12 kWh est 0,683.
Soit $f$ la fonction densité de probabilité de la variable aléatoire $Y$ qui suit la loi normale d'espérance $\mu=9$ et d'écart-type $\sigma=3$ à l'aide de la calculatrice, on trouve f$(9)\approx 0,133$ donc la courbe $C_2$ est la seule des trois courbes qui convient.
Méthode 2 :
La courbe représentative de la fonction de densité de probabilité de la variable aléatoire $Y$ qui suit la loi normale d'espérance $\mu=9$ et d'écart-type $\sigma=3$ admet pour axe de symétrie la droite d'équation $x=9$ donc la courbe $C_3$ ne convient pas.
L'aire du domaine compris entre la courbe représentative de la fonction de densité de probabilité de la variable aléatoire $Y$, l'axe des abscisses et les droites d'équation $x=6$ et $x=12$ est égale à 0,683. Donc la courbe $C_1$ ne convient pas.
La courbe $C_2$ est la courbe représentative de la fonction de densité de probabilité de la variable aléatoire $Y$.
2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
Exercice 3 : 4 points
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l'évaluation.
Une réponse non justifiée ne rapporte aucun point.
- Soit $f$ la fonction définie sur $]0~;~+\infty[$ par $f(x) = 3\ln x$. Le coefficient directeur de la tangente à la courbe représentative de $f$ au point d'abscisse 1 est 3.
- On considère le nombre complexe $z = \dfrac{5\sqrt{3}}{2} - \dfrac{5}{2}\text{i}$. L'écriture exponentielle du conjugué de $z$ est $\overline{z} = 5\text{e}^{\text{i}\frac{5\pi}{6}}$.
- La valeur moyenne de la fonction $x \longmapsto \sin \left(x -\dfrac{\pi}{2}\right)$ sur l'intervalle $[0~;~\pi]$ est égale à $0$.
- La fonction définie pour tout réel $x$ par $f(x) = 3 \cos 5x$ est solution de l'équation différentielle $y'' + 25y = 0$.
Correction de l'exercice 3 (4 points)
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l'évaluation.
Une réponse non justifiée ne rapporte aucun point.
- Soit $f$ la fonction définie sur $]0~;~+\infty[$ par $f(x) = 3\ln x$. Le coefficient directeur de la tangente à la courbe représentative de $f$ au point d'abscisse 1 est 3. Le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse 1 est égal au nombre dérivé $f'(1)$.
- On considère le nombre complexe $z = \dfrac{5\sqrt{3}}{2} - \dfrac{5}{2}\text{i}$. L'écriture exponentielle du conjugué de $z$ est $\overline{z} = 5\text{e}^{\text{i}\frac{5\pi}{6}}$. Le conjugué de $z$ est $\overline{z} =\dfrac{5\sqrt{3}}{2} + \dfrac{5}{2}\text{i}$
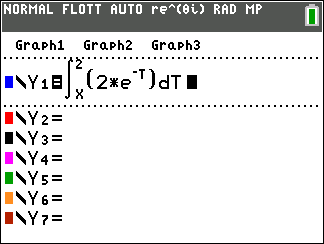
- La valeur moyenne de la fonction $x \longmapsto \sin \left(x -\dfrac{\pi}{2}\right)$ sur l'intervalle $[0~;~\pi]$ est égale à $0$. Tout d'abord, on remarque que $ \sin \left(x -\dfrac{\pi}{2}\right)=-\cos x$ La valeur moyenne de la fonction $x \longmapsto \sin \left(x -\dfrac{\pi}{2}\right)$ sur l'intervalle $[0~;~\pi]$ est : $$\begin{array}{rl} V_{\text{Moy}}&=\frac{1}{\pi -0} \displaystyle\int_0^{\pi} -\cos x \text{d} x\\ &=\left [ -\sin x \right ] _0^{\pi}\\ &= -\sin \pi-(-\sin 0)\\ &=0 \end{array}$$ La proposition 3 est vraie.
- La fonction définie pour tout réel $x$ par $f(x) = 3 \cos 5x$ est solution de l'équation différentielle $y'' + 25y = 0$. Les solutions de l'équation différentielle $y"+25y=0$ ( du type $y"+\omega ^2y=0$ où $\omega=5$) sont les fonctions définies sur $\mathbb R$ par $x\longmapsto A \cos (5x)+B\sin (5x)$ où $A$ et $B$ sont deux constantes réelles quelconques.
La dérivée de $f$ est la fonction définie sur l'intervalle $]0;+\infty[$ par $f'(x)=\dfrac{3}{x}$. D'où $f'(1)=3$.
La proposition 1 est vraie.
$$\begin{array}{cc} \text{ Module }& \text{ Argument} \\ \begin{array}{rl|rl} |\overline{z} |&=\sqrt{a^2+b^2} \\ & =\sqrt{ \left (\dfrac{5\sqrt{3}}{2}\right )^2+ \left ( \dfrac{5}{2} \right )^2}\\ &=\sqrt{25\times \frac{3}{4} +\frac{25}{4}}\\ &=5 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{\sqrt 3}{2} \\ ~\sin \theta=\frac{b}{r}~=\frac{1}{2} \end{array} \right.\\ &\text{ Donc } \theta = \frac{\pi}{6} \text{ convient } \end{array}$$ $$\overline{z}= \dfrac{5\sqrt{3}}{2} + \dfrac{5}{2}\text{i}= 5\left(\cos\left(\frac{\pi}{6} \right) +i\sin \left(\frac{\pi}{6} \right) \right) =5\text{e}^{\text{i}\frac{\pi}{6} }$$ La proposition 2 est fausse.
En choisissant $A=3$ et $B=0$, la fonction $f$ définie pour tout réel $x$ par $f(x)=3\cos (5x)$ est une solution de l'équation différentielle $y″+25y=0.$
La proposition 4 est vraie.
Exercice 4 : 6 points
- Une commune de 2 000 habitants au 1er janvier 2018 voit sa population augmenter de 5 % tous les ans. Pour tout entier naturel $n$, on note $h_n$ le nombre d'habitants de l'année $2018 + n$ : on a donc $h_0 = 2 000$.
La suite $\left(h_n\right)$ est une suite géométrique. Exprimer $h_n$ en fonction de $n$.
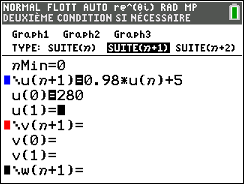
La municipalité de cette commune a conclu un marché avec un fournisseur d'accès internet qui engage ce dernier à fournir un débit total de 16000 Mbit/s au 1er janvier 2018 et à augmenter ce débit de 2,9 % par an. Pour tout entier naturel $n$, on note $d_n$ le débit total dont la commune dispose l'année $2018 + n$. On modélise ainsi le débit par la suite $\left(d_n\right)$. On a alors $d_n = 16000 \times 1,029^n$. - On s'intéresse maintenant au débit par habitant en supposant que celui-ci est réparti équitablement et que toute la population bénéficie d'une connexion internet individuelle. Pour tout entier naturel $n$ on note $u_n$ le débit par habitant pour l'année $2018 + n$ et on admet que $u_n = \dfrac{d_n}{h_n}$.
- Calculer $u_0$ et $u_1$.
- Montrer pour tout entier naturel $n$ on a $u_n = 8 \times 0,98^n$.
- En déduire la nature de la suite $\left(u_n\right)$ et ses caractéristiques.
- Déterminer la limite de la $\left(u_n\right)$. Interpréter ce résultat dans le contexte de l'énoncé.
- Le marché passé avec le fournisseur d'accès internet prévoit également que si le débit passe en dessous de 5 Mbit/s par habitant alors ce dernier doit changer la technologie utilisée pour la réalisation de son réseau.
- On admet que la suite $\left(u_n\right)$ est décroissante. Recopier et compléter l'algorithme ci-dessous afin qu'il permette de déterminer dans combien d'années le débit sera considéré comme insuffisant. $$ \begin{array}{|l|}\hline U\gets 8\\ N \gets 0\\ \text{Tant que }\:U \ldots\\ \hspace{0.8cm}U \gets \ldots\\ \hspace{0.8cm}N \gets N+1~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$
- En quelle année le fournisseur d'accès sera-t-il dans l'obligation de changer sa technologie?
Exercice 4 : 6 points
- Une commune de 2 000 habitants au 1er janvier 2018 voit sa population augmenter de 5 % tous les ans. Pour tout entier naturel $n$, on note $h_n$ le nombre d'habitants de l'année $2018 + n$ : on a donc $h_0 = 2 000$.
La suite $\left(h_n\right)$ est une suite géométrique. Exprimer $h_n$ en fonction de $n$.
La municipalité de cette commune a conclu un marché avec un fournisseur d'accès internet qui engage ce dernier à fournir un débit total de 16000 Mbit/s au 1er janvier 2018 et à augmenter ce débit de 2,9 % par an. Pour tout entier naturel $n$, on note $d_n$ le débit total dont la commune dispose l'année $2018 + n$. On modélise ainsi le débit par la suite $\left(d_n\right)$. On a alors $d_n = 16000 \times 1,029^n$. - On s'intéresse maintenant au débit par habitant en supposant que celui-ci est réparti équitablement et que toute la population bénéficie d'une connexion internet individuelle. Pour tout entier naturel $n$ on note $u_n$ le débit par habitant pour l'année $2018 + n$ et on admet que $u_n = \dfrac{d_n}{h_n}$.
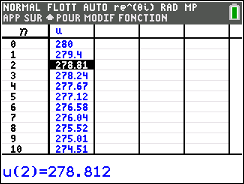
- Calculer $u_0$ et $u_1$. $u_0=\dfrac{d_0}{h_0}$ soit $u_0=\dfrac{16000}{2000}=8$ et $u_1=\dfrac{d_1}{h_1}$ soit $u_1=\dfrac{16000\times 1,029}{2000\times 1,05}\approx 7,84$
- Montrer pour tout entier naturel $n$ on a $u_n = 8 \times 0,98^n$. Pour tout entier naturel $n$ on a : $$\begin{array}{rl} u_n&=\dfrac{d_n}{h_n} \\ & =\dfrac{16000\times 1,029^n}{2000\times 1,05^n}\\ &=8 \times \dfrac{ 1,029^n}{ 1,05^n}\\ &=8 \times\left (\dfrac{ 1,029 }{ 1,05 }\right )^n\\ &=8 \times 0,98^n \\ \end{array}$$ Ainsi, pour tout entier naturel $n$ on a $u_n=8 \times 0,98^n$.
- En déduire la nature de la suite $\left(u_n\right)$ et ses caractéristiques. Pour tout entier naturel $n$ on a $u_n=8 \times 0,98^n$ donc $\left(u_n\right)$ est une suite géométrique de raison $q=0,98$ et de premier terme $u_0=8$.
- Déterminer la limite de la $\left(u_n\right)$. Interpréter ce résultat dans le contexte de l'énoncé. $0<0,98<1 $ donc $\lim\limits_{n \to +\infty} 0,98^n=0 $ d'où,$\lim\limits_{n \to +\infty} 8\times 0,98^n=0 $
Ainsi, $u_0=8$ et $u_1=7,84$.
$\lim\limits_{n \to +\infty} u_n=0 $ donc à partir d'un certain nombre d'années, le débit sera proche de 0 Mbit/s par habitant. - Le marché passé avec le fournisseur d'accès internet prévoit également que si le débit passe en dessous de 5 Mbit/s par habitant alors ce dernier doit changer la technologie utilisée pour la réalisation de son réseau.
- On admet que la suite $\left(u_n\right)$ est décroissante. Recopier et compléter l'algorithme ci-dessous afin qu'il permette de déterminer dans combien d'années le débit sera considéré comme insuffisant. $$ \begin{array}{|l|}\hline U\gets 8\\ N \gets 0\\ \text{Tant que }\:U \ldots\\ \hspace{0.8cm}U \gets \ldots\\ \hspace{0.8cm}N \gets N+1~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$ $$ \begin{array}{|l|}\hline U\gets 8\\ N \gets 0\\ \text{Tant que }\:U \geq 5\\ \hspace{0.8cm}U \gets 0,98\times U\\ \hspace{0.8cm}N \gets N+1~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$
- En quelle année le fournisseur d'accès sera-t-il dans l'obligation de changer sa technologie? Méthode 1 :
On exécute l'algorithme à la calculatrice, la valeur de la variable $N$ obtenue est $N=24$.
Méthode 2 :
On cherche le plus petit entier naturel $n$ solution de l'inéquation $8\times 0,98^n<5$ : $$\begin{array}{rll} u_n< 5 & \iff 8\times 0,98^n<5 &\\ & \iff 0,98^n <\frac{5}{8}&\\ &\iff \ln\left (0,98^n\right ) <\ln \left ( \frac{5}{8}\right )& \ln \text{est strictement croissante sur } ]0;+\infty[\\ &\iff n\ln\left (0,98 \right ) <\ln \left ( \frac{5}{8}\right )& \text{ car } \ln\left (a^n \right )=n\ln a\\ &\iff n> \dfrac{\ln \left ( \frac{5}{8}\right )}{\ln\left (0,98 \right )}&\text{ car } 0,98 <1 \text{ donc } \ln\left (0,98 \right ) <0\\ \end{array}$$ Grâce à une calculatrice, on obtient $\dfrac{\ln \left ( \frac{5}{8}\right )}{\ln\left (0,98 \right )}\approx 23,3$.
donc le plus petit entier naturel $n$ solution de l'inéquation $8\times0,98^n <5$ est $n=24$.
Selon ce modèle, c'est en 2042 que le fournisseur d'accès sera dans l'obligation de changer sa technologie.
- Vues: 18875

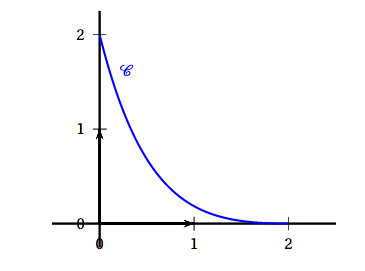
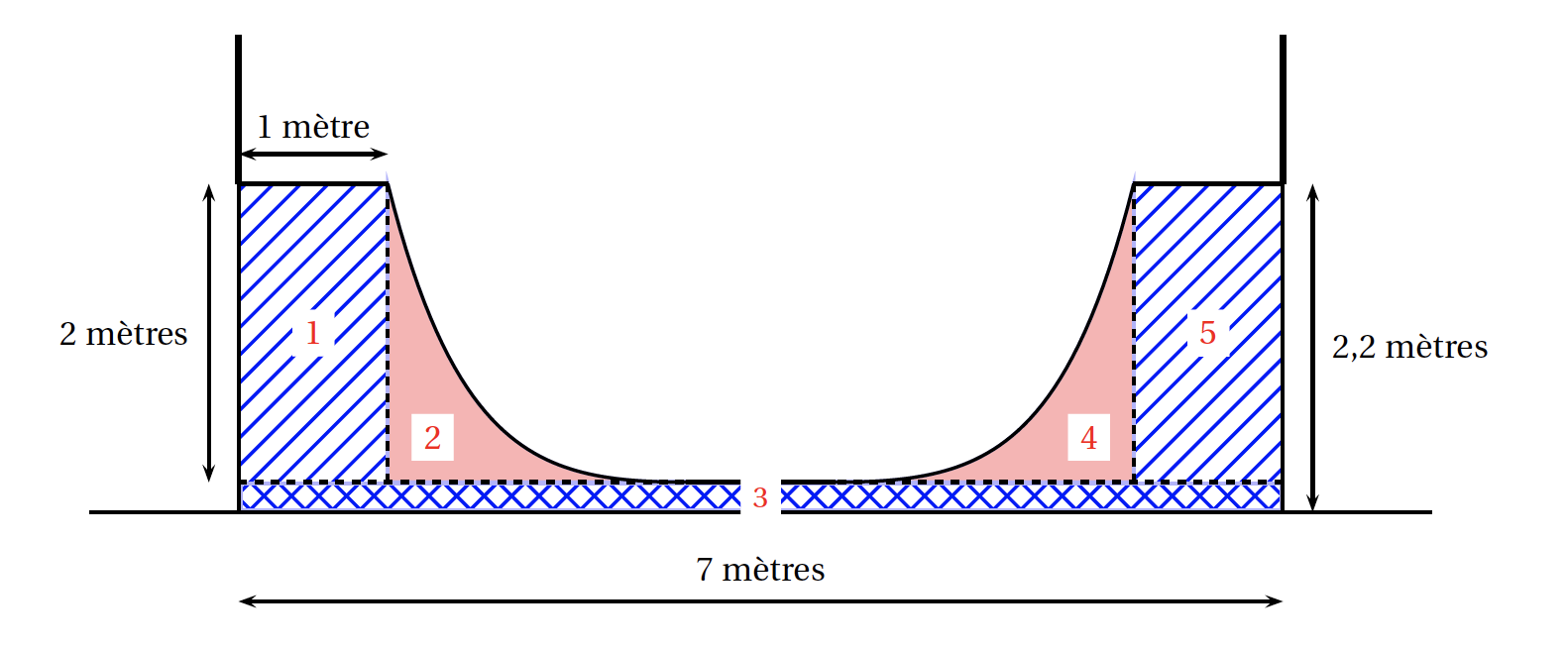
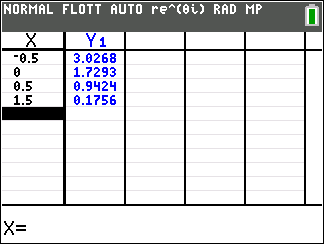
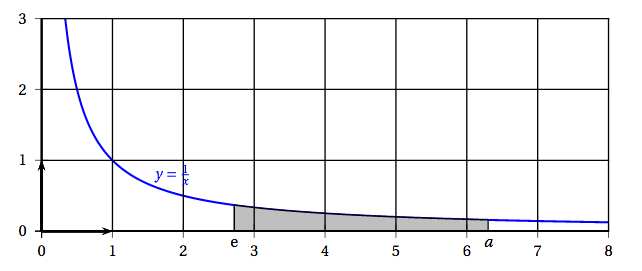 La surface grisée a une aire strictement comprise entre 1 et $1,5$ unité d'aire lorsque $a$ est égal à:
La surface grisée a une aire strictement comprise entre 1 et $1,5$ unité d'aire lorsque $a$ est égal à: