Baccalauréat STI2D Métropole - La Réunion - 18 juin 2019 - Correction Exercice 1

Page 2 sur 8: Correction Exercice 1

Correction de l'exercice 1 (4 points)

QCM Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes,une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante choisie.

1. Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
   On note $z_A$ l'affixe d'un point $A$ appartenant au cercle de centre $O$ et de rayon 4. La partie réelle de $z_A$ est positive et sa partie imaginaire est égale à 2.
   1. $4\text{e}^{-\text{i}\frac{\pi}{6}}$
   2. $-4\text{e}^{\text{i}\frac{\pi}{6}}$
   3. $4\text{e}^{\text{i}\frac{\pi}{6}}$
   4. $-4 \text{e}^{-\text{i}\frac{\pi}{6}}$
Une figure :

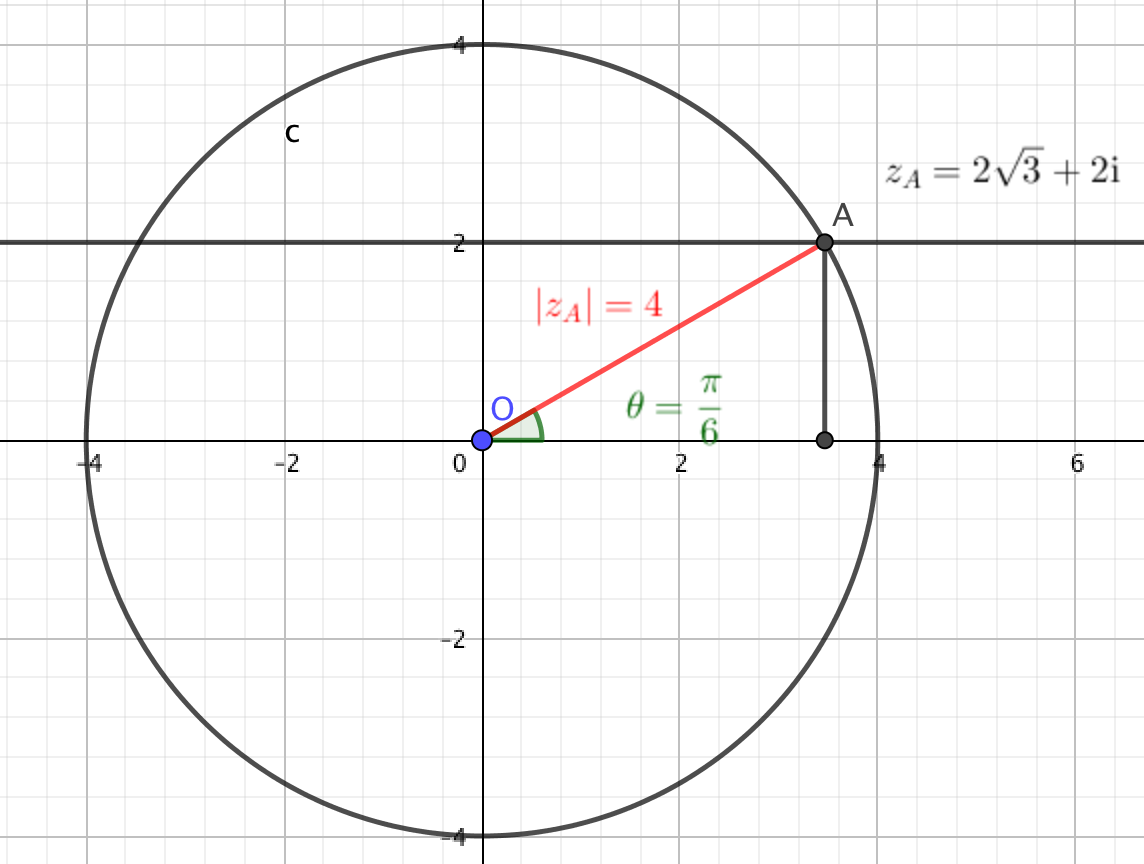
On a ainsi $z_A=2\sqrt 3 +2\text{i}$. $$\begin{array}{cc} \text{Module} & \text{Argument} \\ \begin{array}{rl|rl} |z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ \left (2\sqrt 3\right )^2+2^2}\\ &=\sqrt {16}\\ &= 4 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{2\sqrt 3}{4}=\frac{\sqrt 3}{2}\\ ~\sin \theta=\frac{b}{r}~= \frac{2}{4}= \frac{1}{2} \end{array} \right.\\ &\text{ Donc } \theta = \frac{\pi}{6} \text{ convient } \end{array}$$ $$z= 2 \sqrt 3+2\text{i}= 4\left(\cos\left(\frac{\pi}{6} \right) +i\sin \left(\frac{\pi}{6} \right) \right) =4\text{e}^{\text{i}\frac{\pi}{6}}$$
Bonne réponse : c
2. Le nombre -3 est solution de l'équation :
   1. $\ln (x)=-\ln(3)$
   2. $ \ln\left (\text{e}^x\right )=-3$
   3. $ \text{e}^{\ln(x)} =3$
   4. $\text{e}^x=3$
$ \ln\left (\text{e}^x\right )=-3 \iff x=-3$ car pour tout réel $x$ on a : $ \ln\left (\text{e}^x\right )=x$
Bonne réponse : b
3. On considère la fonction $g$ définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par $g(x) = \dfrac{\text{e}^x}{2x+1})$.
   La fonction $g$ est dérivable sur l'intervalle $\left ]-\frac{1}{2}~;~+ \infty\right [$ et sa fonction dérivée est définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par :
   1. $g'(x) =\dfrac{\text{e}^x}{2}$
   2. $g'(x) = \dfrac{\text{e}^x}{\left (2x+1\right )^2})$
   3. $g'(x) = \dfrac{(2x+3)\text{e}^x}{\left (2x+1\right )^2})$
   4. aucune des réponses précédentes

$g$ est dérivable comme quotient de deux fonctions dérivables dont le dénominateur ne s'annule pas sur $\left ]-\frac{1}{2}~;~+ \infty\right [$. $g=\dfrac{u}{v}$ d'où $g'=\dfrac{u'v-v'u}{v^2}$ avec pour tout réel $x$, dans $\left ]-\frac{1}{2}~;~+ \infty\right [$ : $\left\{ \begin{array}{l} u(x)~ = \text{e}^x\\ v(x)~ =2x+1 \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = \text{e}^x \\ v'(x)~ = 2\end{array}\right.$ $$ \begin{array}{cl} g'(x)&=\dfrac{\text{e}^x(2x+1)-2\text{e}^x }{\left (2x+1\right )^2}\\ & = \dfrac{\text{e}^x(2x+1-2) }{\left (2x+1\right )^2}\\ &= \dfrac{\text{e}^x(2x-1) }{\left (2x+1\right )^2}\\ \end{array} $$ Bonne réponse : d on obtient $g'(x) = \dfrac{(2x-1)\text{e}^x}{\left (2x+1\right )^2} $
4. On considère l'équation différentielle $y" + 4y = 0$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et deux fois dérivable sur $\mathbb R$.
   Une fonction $f$, solution de cette équation différentielle qui vérifie $f(0) = 1$ est définie sur $\mathbb R$ par :
   1. $f(x)=\text{e}^{2x} $
   2. $f(x)=\cos(2x)$
   3. $f(x)=\sin(2x)$
   4. $f(x)=\cos(4x)$
L'équation différentielle $y" + 4y = 0$ est du type $y"+\omega^2 y=0$ où $\omega =2$.
Les solutions de l'équation différentielle $y"+4y=0$ sont les fonctions définies sur $\mathbb R$ par $x\longmapsto A \cos⁡ (2⁢x)+B\sin⁡ (2x)$ où $A$ et $B$ sont deux constantes réelles quelconques.
$f(0) = 1\iff A \cos⁡ (0)+B\sin⁡ (0)=1\iff A =1$ En choisissant $A=1$ et $B=0$, la fonction $f$ définie pour tout réel $x$ par $f⁡(x)= \cos⁡ (2⁢x)$ est une solution de l'équation différentielle $y″+4y=0 $ qui vérifie $f(0) = 1$

Bonne réponse : b