Baccalauréat S Centres étrangers 13 juin 2019 - Exercice 4

Page 7 sur 10: Exercice 4

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

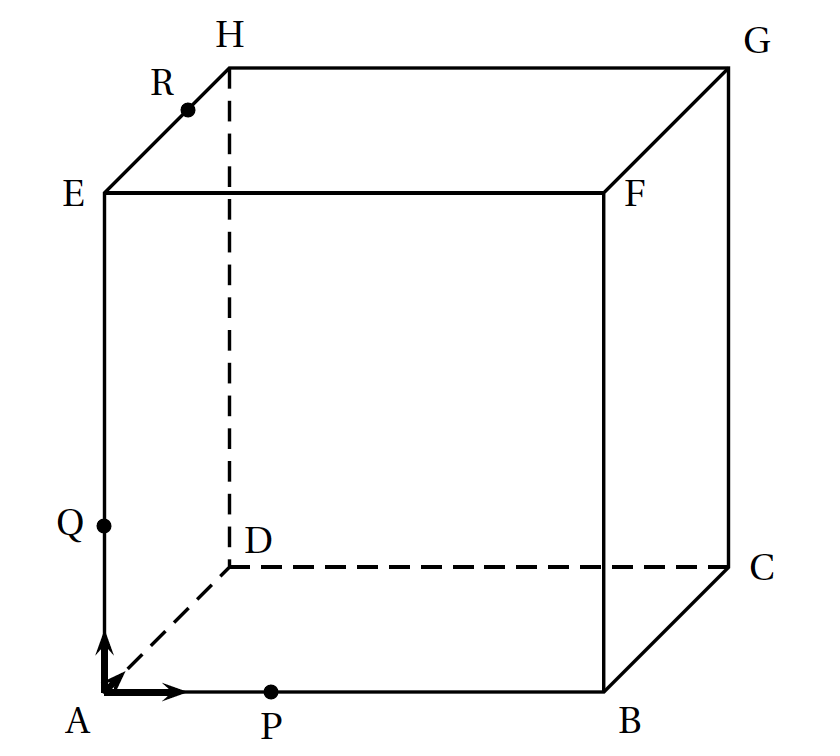
Dans l'espace, on considère un cube ABCDEFGH de centre $\Omega$ et d'arête de longueur $6$. Les points P, Q et R sont définis par : \[\vec{\text{AP}} = \dfrac{1}{3}\vec{\text{AB}},\: \vec{\text{AQ}} = \dfrac{1}{3}\vec{\text{AE}} \: \text{et}\: \vec{\text{HR}} = \dfrac{1}{3}\vec{\text{HE}}.\] Dans tout ce qui suit on utilise le repère orthonormé $\left(\text{A}~;~\vec{\imath},~\vec{\jmath},\vec{k}\right)$ avec : \[\vec{\imath} = \dfrac{1}{6}\vec{\text{AB}},\: \vec{\jmath} = \dfrac{1}{6}\vec{\text{AD}}\:\: \text{et}\:\: \vec{k} =\dfrac{1}{6}\vec{\text{AE}}.\] Dans ce repère, on a par exemple: \[\text{B}(6~;~0~;~0), \text{F}(6~;~0~;~6)\: \text{et }\:\: \text{R}(0~;~4~;~6).\]

1. 1. Donner, sans justifier, les coordonnées des points P, Q et $\Omega$.
   2. Déterminer les nombres réels $b$ et $c$ tels que $\vec{n}(1~;~b~;~c)$ soit un vecteur normal au plan (PQR) .
   3. En déduire qu'une équation du plan (PQR) est : $x - y+ z - 2 = 0$.
2. 1. On note $\Delta$ la droite perpendiculaire au plan (PQR) passant par le point $\Omega$, centre du cube. Donner une représentation paramétrique de la droite $\Delta$.
   2. En déduire que la droite $\Delta$ coupe le plan (PQR) au point I de coordonnées $\left(\dfrac{8}{3}~;~\dfrac{10}{3}~;~\dfrac{8}{3}\right)$.
   3. Calculer la distance $\Omega I$
3. On considère les points J$(6~;~4~;~0)$ et K$(6~;~6~;~2)$.
   1. Justifier que le point J appartient au plan (PQR).
   2. Vérifier que les droites (JK) et (QR) sont parallèles.
   3. Sur la figure donnée en annexe, tracer la section du cube par le plan (PQR). On laissera apparents les traits de construction, ou bien on expliquera la démarche.