Baccalauréat S Métropole 20 juin 2013
Exercice 1 4 points
Une jardinerie vend de jeunes plants d'arbres qui proviennent de trois horticulteurs : 35 % des plants proviennent de l'horticulteur H$_{1}$, 25 % de l'horticulteur H$_{2}$ et le reste de l'horticulteur H$_{3}$. Chaque horticulteur livre deux catégories d'arbres : des conifères et des arbres à feuilles. La livraison de l'horticulteur H$_{1}$ comporte 80 % de conifères alors que celle de l'horticulteur H$_{2}$ n'en comporte que 50 % et celle de l'horticulteur H$_{3}$ seulement 30 %.
- Le gérant de la jardinerie choisit un arbre au hasard dans son stock.
On envisage les événements suivants :- $H_{1}$ : «l'arbre choisi a été acheté chez l'horticulteur H$_{1}$ »,
- $H_{2}$ : «l'arbre choisi a été acheté chez l'horticulteur H$_{2}$ »,
- $H_{3}$ : «l'arbre choisi a été acheté chez l'horticulteur H$_{3}$ »,
- $C$ : «l'arbre choisi est un conifère »,
- $F$ : «l'arbre choisi est un arbre feuillu ».
- Construire un arbre pondéré traduisant la situation.
- Calculer la probabilité que l'arbre choisi soit un conifère acheté chez l'horticulteur H$_{3}$.
- Justifier que la probabilité de l'évènement $C$ est égale à $0,525$.
- L'arbre choisi est un conifère. Quelle est la probabilité qu'il ait été acheté chez l'horticulteur H$_1$ ? On arrondira à $10^{-3}$.
- On choisit au hasard un échantillon de $10$ arbres dans le stock de cette jardinerie. On suppose que ce stock est suffisamment important pour que ce choix puisse être assimilé à un tirage avec remise de $10$ arbres dans le stock. On appelle $X$ la variable aléatoire qui donne le nombre de conifères de l'échantillon choisi.
- Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
- Quelle est la probabilité que l'échantillon prélevé comporte exactement $5$ conifères?
On arrondira à $10^{-3}$. - Quelle est la probabilité que cet échantillon comporte au moins deux arbres feuillus ? On arrondira à $10^{-3}$.
Correction de l'exercice 1 (4 points)
-
- Un arbre pondéré représentant la situation :
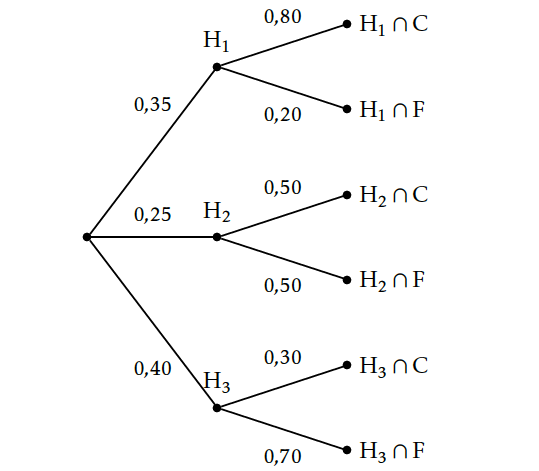
- On veut calculer $p\left (H_3\cap C\right )=p\left (H_3 \right )\times p_{H_3}\left (C\right )=0,40\times 0,50=0,20$
$p\left (H_3\cap C\right )=0,20$ - Calculons la probabilité de l'événement $C$.
$C=\left (H_1\cap C \right )\cup \left (H_2\cap C \right )\left (H_3\cap C \right )$.
La formule des probabilités totales donne
$$p\left (H_1\cap C \right )+p \left (H_2\cap C \right )+p\left (H_3\cap C \right )=p(H_1)\times p_{H_1}(C)+p(H_2) \times p_{H_2}(C)+p(H_3)\times p_{H_3}(C)$$
soit $p(C)= 0,35\times 0,80+ 0,25\times 0,50+ 0,40\times 0,30=0,525$
$p(C)=0,525$ - On veut calculer la probabilité de l'événement &\laquo; L'arbre a été acheté chez $H_1$ sachant que c'est un conifère&\raquo; .
soit à calculer la probabilité conditionnelle $p_{C}\left (H_1\right )=\dfrac{p\left (H_1\cap C\right )}{p(C)}=\dfrac{0,35\times 0,80}{0,525}$
$p_{C}\left (H_1\right )\approx 0,533$
- Un arbre pondéré représentant la situation :
-
- On est en présence d'un schéma de Bernoulli: Succès : &\laquo; l'arbre choisi au hasard est un conifère &\raquo; avec la probabilité $p=0,525 $
Echec : &\laquo; l'arbre choisi au hasard est un arbre à feuilles&\raquo; avec la probabilité $q=1-p= 0,475$
On répète 10 fois cette expérience de façon indépendante et on considère la variable aléatoire $X$ qui comptabilise le nombre de succès .
$X$ suit la loi binomiale $\mathcal{B}\left (10;0,525\right )$ de paramètres $n=10$ et $p=0,525$ - Calculons la probabilité que l'échantillon prélevé contienne exactement 5 conifères et donnons-en une valeur approchée à $10^{-3}$, près.
Pour tout entier $k \in[0;10]$; on a : $$p(X=k)=\binom{10}{k}\times 0,525^k\times0,475^{10-k}.$$ On veut $p(X=5) \binom{10}{5}\times 0,525^5\times0,475^5.$
$p(X=5)\approx 0,243$ - Calculons la probabilité que l'échantillon prélevé contienne au moins deux arbres feuillus et donnons-en une valeur approchée à $10^{-3}$, près.
On veut calculer ici la probabilité de l'événement $X\leq 8$
$p(X \leq 8)=1-p(X>8)=1-p(X=9)-p(X=10)=1-\binom{10}{9}\times 0,525^9\times0,475^1-\binom{10}{10}\times 0,525^10 \approx 0,984 $
La probabilité que l'échantillon prélevé contienne au moins deux arbres feuillus est environ $0,984$ à $10^{-3}$, près.
Remarque :$P(X\leq 8)$ peut s'obtenir avec la calculatrice par :$binomFR\text{é}p(10,0.525,8)$
- On est en présence d'un schéma de Bernoulli: Succès : &\laquo; l'arbre choisi au hasard est un conifère &\raquo; avec la probabilité $p=0,525 $
Exercice 2 7 points
Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé $\left(\text{O}, \vec{i}, \vec{j}\right)$, la courbe représentative $\mathcal{C}$ d'une fonction $f$ définie et dérivable sur l'intervalle $] 0 ; + \infty[$. 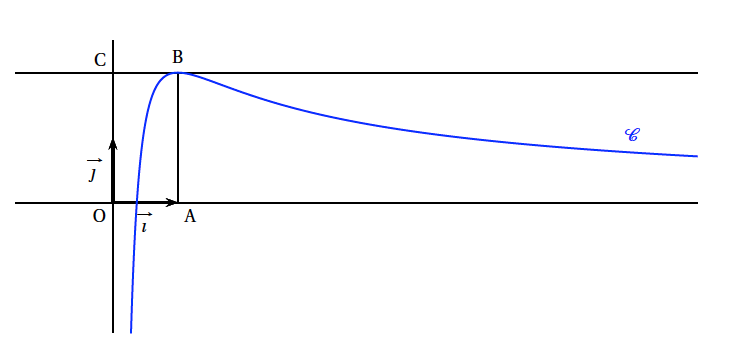
On dispose des informations suivantes :
- les points A, B, C ont pour coordonnées respectives (1, 0), (1, 2), (0, 2);
- la courbe $\mathcal{C}$ passe par le point B et la droite (BC) est tangente à $\mathcal{C}$ en B;
- il existe deux réels positifs $a$ et $b$ tels que pour tout réel strictement positif $x$,
\[f(x) = \dfrac{a+ b\ln x}{x}. \]
-
- En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
- Vérifier que pour tout réel strictement positif $x,\: f'(x) = \dfrac{(b - a) - b \ln x}{x^2}$.
- En déduire les réels $a$ et $b$.
-
- Justifier que pour tout réel $x$ appartenant à l'intervalle $]0\,, +\infty[,\: f'(x)$ a le même signe que $- \ln x$.
- Déterminer les limites de $f$ en 0 et en $+ \infty$. On pourra remarquer que pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x} + 2\;\dfrac{\ln x}{x}$.
- En déduire le tableau de variations de la fonction $f$.
-
- Démontrer que l'équation $f(x) = 1$ admet une unique solution $\alpha$ sur l'intervalle $]0\,, 1]$.
- Par un raisonnement analogue, on démontre qu'il existe un unique réel $\beta$ de l'intervalle $]1\,, + \infty]$ tel que $f(\beta) = 1$. Déterminer l'entier $n$ tel que $n < \beta < n + 1$.
- On donne l'algorithme ci-dessous.
$$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 0. } \\ & \text{ Affecter à } b \text{ la valeur 1. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$- Faire tourner cet algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
$$\begin{array}{|c|c|c|c|c|c|}\hline &\text{étape 1 }&\text{étape 2 }&\text{étape 3 }&\text{étape 4 }&\text{étape 5 }\\ \hline a&0&&&&\\ \hline b&1&&&&\\ \hline b - a&&&&&\\ \hline m&&&&&\\ \hline \end{array}$$ - Que représentent les valeurs affichées par cet algorithme ?
- Modifier l'algorithme ci-dessus pour qu'il affiche les deux bornes d'un encadrement de $\beta$ d'amplitude $10^{-1}$.
- Faire tourner cet algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
- Le but de cette question est de démontrer que la courbe $\mathcal{C}$ partage le rectangle OABC en deux domaines d'aires égales.
- Justifier que cela revient à démontrer que $\displaystyle\int_{\frac{1}{\text{e}}}^1 f(x)\:\text{d}x = 1$.
- En remarquant que l'expression de $f(x)$ peut s'écrire $\dfrac{2}{x} + 2 \times \dfrac{1}{x} \times \ln x$, terminer la démonstration.
Correction de l'exercice 2 (7 points)
Sur le graphique ci-dessous, on a tracé , dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, la courbe représentative $ \mathcal{C}$ d'une fonction $f$ définie et dérivable sur l'intervalle $]0;+\infty[$.
On dispose des informations suivantes:
- Les points $A, B, C$ ont pour coordonnées respectives (1, 0), (1, 2), (0, 2);
- la courbe $ \mathcal{C}$ passe par le point $B$ et la droite $(BC)$ est tangente à $ \mathcal{C}$ en $B$;
- il existe deux réels positifs $a$ et $b$ tels que pour tout réel strictement positif $x$, $f(x)=\dfrac{a+b\ln x }{x}$
-
- En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
Le point $B(1,2)$ est un point de $ \mathcal{C}$, donc $f(1)=2$
La tangente à $ \mathcal{C}$ au point $B$ d'abscisse 1 est horizontale , donc $f'(1)=0$.
$f(1)=2$ et $f'(1)=0$. - Vérifier que pour tout réel strictement positif $x, f'(x)=\dfrac{(b-a)-b\ln x }{x^2} $
$f=\dfrac{u}{v}$, donc $f'=\dfrac{u'v-v'u}{v^2}$
ici $u(x)=a+b\ln x$ et $v(x)=x$
on a donc $u'(x)=\dfrac{b}{x}$ et $v'(x)=1$
puis $f'(x)=\dfrac{\dfrac{b}{x}\times x -1\times \left (a+b\ln x\right )}{x^2}=\dfrac{b-a-b\ln x }{x^2} $
$f'(x)=\dfrac{(b-a)-b\ln x }{x^2} $. - En déduire les réels $a$ et $b$.
$f(1)=2 $ donc $\dfrac{a+b \ln 1}{1}=2$ donc $ a=2$, en effet $\ln 1=0$.
$f'(1)=0$ donc $ \dfrac{(b-a)-b\ln 1 }{1^2}=0 $ donc $ b-a=0 $ donc $ b=a=2$
$a=2$ et $b=2$ ainsi $f(x)=\dfrac{2+2\ln x }{x}$
- En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
-
- Justifier que pour tout réel $x$ appartenant à l'intervalle $]0;+\infty[$ , $f'(x)$ a le même signe que $-\ln x $.
D'après la question 1. $f'(x)=\dfrac{(b-a)-b\ln x }{x^2} =\dfrac{-2 \ln x }{x^2}$, on a remplacé $a$ et $b$ par 2.
Comme on travaille sur $]0;+\infty[$, on a $x^2>0$ et 2>0 ,
donc $f'(x)$ a le signe de $-\ln x$. - Déterminer les limites de $f$ en 0 et en $+\infty$.
On pourra remarquer que pour tout réel $x$ strictement positif, $f(x)=\dfrac{2}{x} +\dfrac{2\ln x}{x}$
- Limite en $0^+$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\left (2+2\ln x\right )\times \dfrac{ 1}{x}$
$\left.\begin{array}{l} \lim\limits_{x \to 0^+} (2+2\ln x)=-\infty\\ \lim\limits_{x \to 0^+}~\dfrac{1}{x}=+\infty \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to 0^+}~f(x)=-\infty$ - Limite en $+\infty$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\dfrac{2}{x} +\dfrac{2\ln x}{x}$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~\dfrac{2}{x}=0\\ \lim\limits_{x \to +\infty}~\dfrac{2\ln x}{x}=0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to +\infty}~f(x)=0$
On a utilisé la limite de référence :$\lim\limits_{x \to +\infty}~\dfrac{ \ln x}{x}=0$
$\lim\limits_{x \to +\infty}~f(x)=0$
- Limite en $0^+$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\left (2+2\ln x\right )\times \dfrac{ 1}{x}$
- En déduire le tableau de variation de la fonction $f$. On sait que la dérivée a le signe de $-\ln x $ sur $]0;+\infty[$.
$f'(x)>0 \Leftrightarrow -\ln x > 0 \Leftrightarrow \ln x < 0 \Leftrightarrow0< x<1.$
$f'(x)=0 \Leftrightarrow x=1.$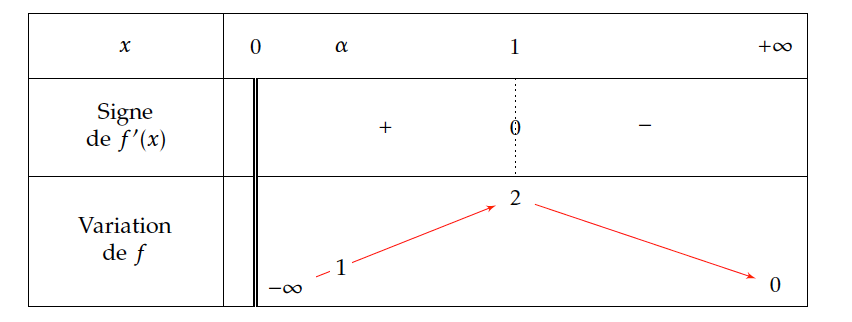
- Justifier que pour tout réel $x$ appartenant à l'intervalle $]0;+\infty[$ , $f'(x)$ a le même signe que $-\ln x $.
-
- Démontrer que l'équation $f(x)=1$ admet une unique solution $\alpha$ sur l'intervalle $]0,1]$.
$\left.\begin{array}{ll} &\bullet \quad f \text{ est continue sur } I=]0;1] \text{ (elle est dérivable sur )} I ;\\ &\bullet \quad f \text{ est strictement croissante sur } I ;\\ &\bullet \quad f(1)=2 ;\\ &\bullet \quad \lim\limits_{x \to 0^+} f(x)=-\infty.\\\end{array}\right\}$ . Comme $1 \in ]-\infty;2]$ l'équation $f(x)=1$ admet une unique solution $\alpha$ dans $I$
Ainsi l'équation $f(x)=1$ admet une unique solution $\alpha$ dans $I$ - Par un raisonnement analogue, on démontre qu'il existe un unique réel $\beta$ de l'intervalle $]1;+\infty[$ tel que $f(\beta )=1$.
Déterminer l'entier $n$ tel que $n< \beta<n+ 1$
soit $f(5)>f(\beta)>f(6)$
comme $f$ est strictement décroissante sur $[1;+\infty[$; on déduit $5<\beta< 6$
$5<\beta< 6$
- Démontrer que l'équation $f(x)=1$ admet une unique solution $\alpha$ sur l'intervalle $]0,1]$.
- On donne l'algorithme ci-dessous.
$$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 0. } \\ & \text{ Affecter à } b \text{ la valeur 1. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$- Faire tourner l'algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
$$\begin{array}{|c|c|c|c|c|c|} \hline &\text{ étape 1 } & \text{ étape 2 } &\text{ étape 3 } &\text{ étape 4 } & \text{ étape 5 } \\ \hline a & 0 & 0 & 0,25 & 0,375 & 0,4375 \\ \hline b & 1 & 0,5 & 0,5 & 0,5 & 0,5 \\ \hline b-a & 1 & 0,5 & 0,25 &0,125 & 0,0625\\ \hline m & 0,5 & 0,25 & 0,375 & 0,4375 & \text{ L'algorithme s'arrête car la condition } b-a\leq 0,1 \text{est réalisée }\\ \hline \end{array}$$ - Que représentent les valeurs affichées par cet algorithme?
Cet algorithme fournit un encadrement à 0,1 près de l'unique solution $\alpha$ de l'équation $f(x)=1$ se trouvant dans l'intervalle $]0,1]$. La méthode utilisée est la dichotomie. - Modifier l'algorithme ci-dessus pour qu'il affiche les deux bornes d'un encadrement de $\beta$ d'amplitude $10^{-1}$.
$$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 5. } \\ & \text{ Affecter à } b \text{ la valeur 6. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$
- Faire tourner l'algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
- Le but de cette question est de démontrer que la courbe $ \mathcal{C}$ partage le rectangle $OABC$ en deux domaines d'aires égales.
- Justifier que cela revient à démontrer que $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$.
Le rectangle $OABC$ a pour aire $\mathcal{A}=OA \times BC =2 (u.a.)$
On résout l'équation $f(x)=0$ sur $]0;+\infty[$
$f(x)=0 \Leftrightarrow \dfrac{2+2\ln x }{x} \Leftrightarrow 2+2\ln x =0 \Leftrightarrow \ln x =-1 \Leftrightarrow x=e^{-1} \Leftrightarrow x=\dfrac{1}{e}$.
La courbe $ \mathcal{C}$ rencontre l'axe des abscisses au point d'abscisse $x=\dfrac{1}{e}$.
On doit donc montrer que l'aire du domaine délimité par la courbe $ \mathcal{C}$ , l'axe des abscisses et les droites d'équation $x=\dfrac{1}{e}$ et $x=1$ vaut $1 u.a.$.
Comme $f$ est continue, positive sur $\left [\dfrac{1}{e};1\right ]$, en effet :
si $x\geq \dfrac{1}{e}$ alors $\ln x\geq \ln\left (\dfrac{1}{e}\right )$
soit $1+\ln x\geq 0$ puis en multipliant par $\dfrac{2}{x}>0$ sur $]0;++\infty[$, on obtient $f(x)\geq 0$,
cette aire vaut $\mathcal{B}= \int_{\dfrac{1}{e}}^{1}f(x)\;dx$.
On doit donc établir $\mathcal{B}=1$ soit $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$. - En remarquant que l'expression de $f(x)$ peut s'écrire $\dfrac{2}{x} +2\times \dfrac{1}{x}\times \ln x $, terminer la démonstration.
$f(x)=\dfrac{2}{x} +2\times \dfrac{1}{x}\times \ln x =2\times \dfrac{1}{x}+2 u'(x)\times u(x)$ où $u(x)=\ln x$ .
On note $F$ une primitive de $f$ sur $]0;+\infty[$.
$F(x)=2\ln x +\left (\ln x \right )^2$. On a utilisé le fait que $u'u^n$ a pour primitive $\dfrac{u^{n+1}}{n+1}$ pour $n\neq -1$.
$$\int_{\dfrac{1}{e}}^{1}f(x)\;dx=F(1)-F\left (\dfrac{1}{e}\right )=2\ln 1 +\left (\ln 1 \right )^2 -\left (2\ln\left (\dfrac{1}{e}\right )+\left (\ln \left (\dfrac{1}{e}\right )\right )^2\right ) =0-(-2+1)=1$$ En effet $\ln\left (\dfrac{1}{e}\right )=-\ln e=-1$
- Justifier que cela revient à démontrer que $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$.
Exercice 3 4 points
Pour chacune des quatre propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
- Proposition 1 : Dans le plan muni d'un repère orthonormé, l'ensemble des points $M$ dont l'affixe $z$ vérifie l'égalité $|z - \text{i}| = |z + 1|$ est une droite.
- Proposition 2 : Le nombre complexe $\left(1 + \text{i}\sqrt{3}\right)^4$ est un nombre réel.
- Soit ABCDEFGH un cube.
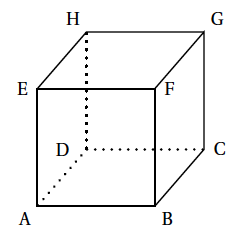 Proposition 3 : Les droites (EC) et (BG) sont orthogonales.
Proposition 3 : Les droites (EC) et (BG) sont orthogonales.
- L'espace est muni d'un repère orthonormé $\left(O,\vec{i},\vec{j},\vec{k}\right)$. Soit le plan $\mathcal{P}$ d'équation cartésienne $x + y + 3z + 4 = 0$. On note S le point de coordonnées $(1\,, -2\,, - 2)$.
Proposition 4 : La droite qui passe par S et qui est perpendiculaire au plan $\mathcal{P}$ a pour représentation paramétrique $\left\{\begin{array}{l @{\;=\;} l} x =&2 + t\\ y=& - 1 + t\\ z=&1 + 3t \end{array}\right.$, $t \in \textbf{R}$.
Correction de l'exercice 3 (4 points)
Pour chacune des quatre propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
- Proposition 1: Dans le plan muni d'un repère orthonormé, l'ensemble des points $M$ dont l'affixe $z$ vérifie l'égalité $|z-i|=|z+1|$ est une droite.
On note $A$ et $B$ les points d'affixes respectives $i$ et $-1$.
$|z-i|=|z+1| \Leftrightarrow |z-i|=|z-(-1)| \Leftrightarrow \left|z_M-z_A \right|=\left|z_M-z_B\right| \Leftrightarrow AM=BM $
L'ensemble cherché est la médiatrice de $[AB]$, la proposition 1 est donc vraie. - Proposition 2: Le nombre complexe $(1+i \sqrt 3 )^4$ est un nombre réel.
On met $u=1+i \sqrt 3$ sous forme exponentielle .
$|u|=\sqrt{1^2+\sqrt 3^2}=\sqrt 4=2$
Ainsi $u=2 \left(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2} \right )=2e^{i\frac{\pi}{3}}$
On a alors $(1+i \sqrt 3 )^4 =\left( 2e^{i\frac{\pi}{3}}\right )^4=2^4e^{i\frac{4\pi}{3}}=16e^{i\frac{4\pi}{3}}=16\left (\cos\left (\frac{4\pi}{3}\right )+i\sin\left (\frac{4\pi}{3}\right )\right)=16\left (-\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}\right)=-8-8i\sqrt3$
Le nombre complexe $(1+i \sqrt 3 )^4$ n'est pas un nombre réel,la proposition 2 est donc fausse.
Remarque (4 étant un petit exposant ) : $(1+i \sqrt 3 )^2=1+2i\sqrt 3-3=-2+2i\sqrt 3$
alors $(1+i \sqrt 3 )^4= \left ((1+i \sqrt 3 )^2\right )^2=(-2+2i\sqrt 3)^2=4-8i\sqrt 3-12=-8-8i\sqrt 3$ - Soit $ABCDEFGH$ un cube.
Proposition 3:Les droites $(EC)$ et $(BG)$ sont orthogonales. Figure On rapporte l'espace au repère orthonormal $\left (A,\vec{AB},\vec{AD},\vec{AE}\right )$ en choisissant $AB$ comme unité de longueur.
On a , dans ce repère $E(0~,0~,1~);C(1~,1~,0~);\vec{EC}(1~, 1~,-1~);$
$B(1~,0~,0~);G(1~,1~,1~);\vec{BG}(0~, 1~, 1~);$
$\vec{EC}.\vec{BG}=xx'+yy'+zz'=0+1-1=0$
Ayant $\vec{EC}.\vec{BG}=0$, les droites $(EC)$ et $(BG)$ sont orthogonales.
Les droites $(EC)$ et $(BG)$ sont orthogonales.La proposition 3 est exacte. - L'espace est muni d'un repère orthonormé $\left(\text{O},\vec{j},\vec{j},\vec{k}\right)$. Soit le plan $P$ d'équation cartésienne $x+y+3z+4=0$. On note S le point de coordonnées (1,2,-2).
Proposition 4: La droite qui passe par $S$ et qui est perpendiculaire au plan $P$ a pour représentation paramétrique : \[\left\{\begin{array}{l c r} x&=&2+t
y&=&-1+t
z&=&1+3t \end{array}\right. \quad \text{avec}~ t \in \mathbb{R}.\] Une droite $D$ perpendiculaire au plan $P$ admet pour vecteur directeur un vecteur normal du plan $P$, soit ici $\vec{n}(1,1,3)$
$S(1,-2,-2) \in D \Leftrightarrow \text{ il existe } t \in \mathbb{R}, \left\{\begin{array}{l c r} x_S&=&2+t\\ y_S&=&-1+t\\ z_S&=&1+3t \\ \end{array}\right. \Leftrightarrow \text{ il existe } t \in \mathbb{R}, \left\{\begin{array}{l c r} 1&=&2+t \\ -2&=&-1+t\\ -2&=&1+3t \\\end{array}\right.$
$S(1,-2,-2) \in D \Leftrightarrow \text{ il existe } t \in \mathbb{R}, \left\{\begin{array}{l c r} t&=&-1 \\ t&=&-1\\ t&=&-1\\ \end{array}\right. $ Il existe bien $t\in \mathbb{R} $ tel que $t=-1$ donc $S( 1,-2,-2)\in D$
La droite $D$ perpendiculaire au plan $P$ passant par $S$ a pour représentation paramétrique : $$\left\{\begin{array}{l c r} x&=&2+t \\ y&=&-1+t\\ z&=&1+3t\\ \end{array}\right. \quad ~ t \in \mathbb{R}.$$
Exercice 4 5 points
Soit la suite numérique $\left(u_{n}\right)$ définie sur $\textbf{N}$ par :
\[u_{0} = 2 \quad \text{et pour tout entier naturel } \:n, \:u_{n+1} = \dfrac{2}{3}u_{n} + \dfrac{1}{3}n + 1.\]
-
- Calculer $u_{1}, u_{2}, u_{3}$ et $u_{4}$. On pourra en donner des valeurs approchées à $10^{- 2}$ près.
- Formuler une conjecture sur le sens de variation de cette suite.
-
- Démontrer que pour tout entier naturel $n$,
\[u_{n} \leqslant n + 3.\] - Démontrer que pour tout entier naturel $n$, \[u_{n+1} - u_{n} = \dfrac{1}{3} \left(n + 3 - u_{n}\right).\]
- En déduire une validation de la conjecture précédente.
- Démontrer que pour tout entier naturel $n$,
- On désigne par $\left(v_{n}\right)$ la suite définie sur $\textbf{N}$ par $v_{n} = u_{n} - n$.
- Démontrer que la suite $\left(v_{n}\right)$ est une suite géométrique de raison $\dfrac{2}{3}$.
- En déduire que pour tout entier naturel $n$, \[u_{n} = 2\left(\dfrac{2}{3} \right)^n + n\]
- Déterminer la limite de la suite $\left(u_{n}\right)$.
- Pour tout entier naturel non nul $n$, on pose: \[S_{n} = \sum_{k=0}^n u_{k} = u_{0} + u_{1} + \ldots + u_{n}\quad \text{et} \quad T_{n} = \dfrac{S_{n}}{n^2}.\]
- Exprimer $S_{n}$ en fonction de $n$.
- Déterminer la limite de la suite $\left(T_{n}\right)$.
Correction de l'exercice 4 (5 points)
Soit la suite numérique $(u_n)$ définie sur $\mathbb{N}$ par:
$u_0=2$ et pour tout entier naturel $n, u_{n+1}=\dfrac{2}{3} u_n+\dfrac{1}{3}n+1.$
-
- Calculer $u_1, u_2, u_3$ et $u_4$. On pourra en donner des valeurs approchées à $ 10^{-2}$ près.
- $n=0$ dans la relation : $u_{n+1}=\dfrac{2}{3} u_n+\dfrac{1}{3}n+1$ donne $u_1=\dfrac{2}{3} u_0+\dfrac{1}{3}\times 0+1=\dfrac{2}{3} \times 2+1=\dfrac{7}{3}\approx 2,33$
- $n=1$ donne $u_2=\dfrac{2}{3} u_1+\dfrac{1}{3}\times 1+1=\dfrac{2}{3} \times \dfrac{7}{3}+\dfrac{1}{3}+1=\dfrac{14}{9}+\dfrac{4}{3}=\dfrac{26}{9}\approx 2,89$
- $n=2$ donne $u_3=\dfrac{2}{3} u_2+\dfrac{1}{3}\times 2+1=\dfrac{2}{3} \times \dfrac{26}{9}+\dfrac{5}{3} =\dfrac{52}{27}+\dfrac{45}{27}=\dfrac{97}{27}\approx 3,59$
- $n=3$ donne $u_4=\dfrac{2}{3} u_3+\dfrac{1}{3}\times 3+1=\dfrac{2}{3} \times \dfrac{97}{27}+2 =\dfrac{194}{81}+\dfrac{162}{81}=\dfrac{356}{81}\approx 4,40$
- Formuler une conjecture sur le sens de variation de cette suite.
Au vu des premiers termes, la suite $(u_n)$ semble strictement croissante.
- Calculer $u_1, u_2, u_3$ et $u_4$. On pourra en donner des valeurs approchées à $ 10^{-2}$ près.
-
- Démontrer que pour tout entier naturel $n,u_n \leq n+3$.
notons $P(n)$ la propriété $u_n \leq n+3$:- Initialisation : $u_0=2$ et $2\leq 3$ donc $P(0)$ est vraie.
- Hérédité : Soit $p\geq0$, on suppose que: $u_p\leq p+3~(HR)$
On doit prouver que : $ u_{p+1}\leq (p+1)+3$, c'est-à-dire $ u_{p+1}\leq p+4$.
On utilise la relation $ u_{p+1}=\dfrac{2}{3} u_p+\dfrac{1}{3}p+1$
En multipliant par $\dfrac{2}{3}>0$ de part et d'autre dans $(HR)$, on obtient : $\dfrac{2}{3} u_p\leq \dfrac{2}{3}\left (p+3~\right )$.
En ajoutant $\dfrac{1}{3}p+1$ de part et d'autre :
$\dfrac{2}{3} u_p +\dfrac{1}{3}p+1\leq \dfrac{2}{3}\left (p+3~\right )+\dfrac{1}{3}p+1$.
soit $u_{p+1}\leq \dfrac{2}{3}p+2+\dfrac{1}{3}p+1$
c'est-à-dire :$u_{p+1}\leq p+3\leq p+4$ - Conclusion : Le principe de récurrence s'appliquant, on a pour tout entier $n\geq 0 ;u_n\leq n+3$
- Démontrer que pour tout entier naturel $n, u_{n+}1-u_n=\dfrac{1}{3}\left (n+3-u_n\right )$.
$ u_{n+1} -u_n=\dfrac{2}{3} u_n+\dfrac{1}{3}n+1-u_n=-\dfrac{1}{3} u_n+\dfrac{1}{3}n+1=\dfrac{1}{3}\left (n+3-u_n\right )$ - En déduire une validation de la conjecture précédente.
D'après 2.a., pour tout $n\geq 0$, $u_n\leq n+3$
donc $n+3-u_n\geq 0$
puis en multipliant par $ \dfrac{1}{3}>0$ , on obtient $\dfrac{1}{3}\left (n+3-u_n\right )\geq 0$
donc pour tout entier $n\geq 0$ , on a $ u_{n+1} -u_n\geq 0$, On a donc prouvé que la suite $(u_n)$ est croissante.
- Démontrer que pour tout entier naturel $n,u_n \leq n+3$.
- On désigne par $(v_n)$ la suite définie sur $\mathbb{N}$ par $v_n=u_n-n$.
- Démontrer que la suite $(v_n)$ est une suite géométrique de raison $\dfrac{2}{3}$.
Pour tout $n\geq 0,v_{n+1}=u_{n+1}-(n+1)= \dfrac{2}{3} u_n+\dfrac{1}{3}n+1-n-1=\dfrac{2}{3} u_n-\dfrac{2}{3}n=\dfrac{2}{3} \left (u_n-n\right )=\dfrac{2}{3}v_n$
Ayant pour tout entier naturel $n; v_{n+1}=\dfrac{2}{3}v_n$ : la suite $(v_n)$ est une suite géométrique de raison $\dfrac{2}{3}$. - En déduire que pour tout entier naturel $n, u_n=2\left (\dfrac{2}{3}\right )^n+n$.
Comme $(v_n)$ est géométrique de raison $\dfrac{2}{3}$, et de plus $v_0=u_0-0=2$;
on a pour tout $n\geq 0, v_n=q^n \times v_0=\left (\dfrac{2}{3}\right )^n\times 2$
De $v_n=u_n-n$ on déduit :$u_n=v_n+n=2\left (\dfrac{2}{3}\right )^n+n$ - Déterminer la limite de la suite $(u_n)$.
$\left.\begin{array}{l} \lim\limits_{n \to +\infty}~2\left (\dfrac{2}{3}\right )^n=0\\ \lim\limits_{n \to +\infty}~n=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{n \to +\infty}~u_n=+\infty$.
On a utilisé la limite de référence :$\lim\limits_{n \to +\infty}q^n=0$ si $-1<q<1$
- Démontrer que la suite $(v_n)$ est une suite géométrique de raison $\dfrac{2}{3}$.
Spécialité 5 points
On étudie la population d'une région imaginaire. Le 1 er janvier 2013, cette région comptait 250000 habitants dont 70 % résidaient à la campagne et 30 % en ville.
L'examen des données statistiques recueillies au cours de plusieurs années amène à choisir de modéliser l'évolution de la population pour les années à venir de la façon suivante :
- l'effectif de la population est globalement constant,
- chaque année, 5 % de ceux qui résident en ville décident d'aller s'installer à la campagne et 1 % de ceux qui résident à la campagne choisissent d'aller habiter en ville.
Pour tout entier naturel $n$, on note $v_{n}$ le nombre d'habitants de cette région qui résident en ville au 1 er janvier de l'année $(2013 + n)$ et $c_{n}$ le nombre de ceux qui habitent à la campagne à la même date.
- Pour tout entier naturel $n$, exprimer $v_{n+1}$ et $c_{n+1}$ en fonction de $v_{n}$ et $c_{n}$.
- Soit la matrice $A = \begin{pmatrix}0,95&0,01\\0,05& 0,99\end{pmatrix}$.
On pose $X = \begin{pmatrix}a\\b\end{pmatrix}$ où $a,\: b$ sont deux réels fixés et $Y = AX$. Déterminer, en fonction de $a$ et $b$, les réels $c$ et $d$ tels que $Y = \begin{pmatrix}c\\d\end{pmatrix}$. Les résultats précédents permettent d'écrire que pour tout entier naturel $n$, - Soient les matrices $P = \begin{pmatrix}1&- 1\\5&1\end{pmatrix}$ et $Q = \begin{pmatrix}1&1\\- 5&1\end{pmatrix}$.
- Calculer $PQ$ et $QP$. En déduire la matrice $P^{-1}$ en fonction de $Q$.
- Vérifier que la matrice $P^{-1}AP$ est une matrice diagonale $D$ que l'on précisera.
- Démontrer que pour tout entier naturel $n$ supérieur ou égal à $1$, $A^n = P D^n P^{- 1}$.
- Les résultats des questions précédentes permettent d'établir que \[v_{n} = \dfrac{1}{6}\left(1 + 5 \times 0,94^n\right)v_{0} + \dfrac{1}{6}\left(1 - 0,94^n\right)c_{0}.\]
Quelles informations peut-on en déduire pour la répartition de la population de cette région à long terme ?
$X_{n+1} = AX_{n}$ où $X_{n} = \begin{pmatrix}v_{n}\\c_{n}\end{pmatrix}$. On peut donc en déduire que pour tout entier naturel $n,\: X_{n} = A^n X_{0}$.
Correction de l'exercice de Spécialité (5 points)
On étudie la population d'une région imaginaire. Le 1 er janvier 2013, cette région comptait 250000 ~habitants dont 70 % résidaient à la campagne et 30 % en ville. L'examen des données statistiques recueillies au cours de plusieurs années amène à choisir de modéliser l'évolution de la population pour les années à venir de la façon suivante :
- l'effectif de la population est globalement constant,
- chaque année, 5 % de ceux qui résident en ville décident d'aller s'installer à la campagne et 1 % de ceux qui résident à la campagne choisissent d'aller habiter en ville.
Pour tout entier naturel $n$, on note $v_{n}$ le nombre d'habitants de cette région qui résident en ville au 1 er janvier de l'année $(2013 + n)$ et $c_{n}$ le nombre de ceux qui habitent à la campagne à la même date.
- Pour tout entier naturel $n$, exprimer $v_{n+1}$ et $c_{n+1}$ en fonction de $v_{n}$ et $c_{n}$.
Chaque année, 5 % de ceux qui résident en ville décident d'aller s'installer à la campagne et 1 % de ceux qui résident à la campagne choisissent d'aller habiter en ville.
Donc pour tout entier naturel $n$, $\left \{ \begin{array}{rcl} v_{n+1} & = & 95\%v_n+1\%c_n \\ c_{n+1} & = & 5\%v_n+99\%c_n \end{array} \right.$
Ainsi $\left \{\begin{array}{rcl} v_{n+1} & = & 0,95v_n+0,01c_n \\ c_{n+1} & = & 0,05v_n+0,99 c_n \end{array} \right.$
$\begin{pmatrix}v_{n+1}\\c_{n+1}\end{pmatrix}=\begin{pmatrix}0,95v_n+0,01c_n\\0,05v_n+0,99 c_n \end{pmatrix}$ - Soit la matrice $A = \begin{pmatrix}0,95&0,01\\0,05& 0,99\end{pmatrix}$. On pose $X = \begin{pmatrix}a\\b\end{pmatrix}$ où $a,\: b$ sont deux réels fixés et $Y = AX$.
Déterminer, en fonction de $a$ et $b$, les réels $c$ et $d$ tels que $Y = \begin{pmatrix}c\\d\end{pmatrix}$.
Comme $A = \begin{pmatrix}0,95&0,01\\0,05& 0,99\end{pmatrix}$ on a $Y = \begin{pmatrix}c\\d\end{pmatrix}=AX=\begin{pmatrix}0,95&0,01\\0,05& 0,99\end{pmatrix}\begin{pmatrix}a\\b\end{pmatrix}=\begin{pmatrix}0,95a+0,01b\\0,05a+0,99b\end{pmatrix}$. $\begin{pmatrix}c\\d\end{pmatrix}=\begin{pmatrix}0,95a+0,01b\\0,05a+0,99b\end{pmatrix}$
Les résultats précédents permettent d'écrire que pour tout entier naturel $n$, $X_{n+1} = AX_{n}$ où $X_{n} = \begin{pmatrix}v_{n}\\c_{n}\end{pmatrix}$. On peut donc en déduire que pour tout entier naturel $n,\: X_{n} = A^n X_{0}$. - Soient les matrices $P = \begin{pmatrix}1&- 1\\5&1\end{pmatrix}$ et $Q = \begin{pmatrix}1&1\\- 5&1\end{pmatrix}$.
- Calculer $PQ$ et $QP$. En déduire la matrice $P^{-1}$ en fonction de $Q$. \\ $P\times Q= \begin{pmatrix}1&- 1\\5&1\end{pmatrix}\times \begin{pmatrix}1&1\\- 5&1\end{pmatrix}=\begin{pmatrix}6&0\\0&6\end{pmatrix}=6 Id_2$ $Q \times P = \begin{pmatrix}1&1\\- 5&1\end{pmatrix}\times \begin{pmatrix}1&- 1\\5&1\end{pmatrix}=\begin{pmatrix}6&0\\0&6\end{pmatrix}=6 Id_2$, donc $P$ est inversible et
$P^{- 1}=\dfrac{1}{6}Q=\dfrac{1}{6} \begin{pmatrix}1&1\\- 5&1\end{pmatrix}$. - Vérifier que la matrice $P^{-1}AP$ est une matrice diagonale $D$ que l'on précisera.
$$P^{-1}AP=\dfrac{1}{6} \underbrace{ \begin{pmatrix}1&1\\- 5&1\end{pmatrix}\times\begin{pmatrix}0,95&0,01\\0,05& 0,99\end{pmatrix}}\times \begin{pmatrix}1&- 1\\5&1\end{pmatrix} $$ $$P^{-1}AP=\dfrac{1}{6} \begin{pmatrix}1&-4,7\\1&0,94\end{pmatrix}\times \begin{pmatrix}1&- 1\\5&1\end{pmatrix} $$ $$P^{-1}AP=\dfrac{1}{6} \begin{pmatrix}6&0\\0&6\end{pmatrix}=\begin{pmatrix}1&0\\0&0,94\end{pmatrix} $$
On a donc $P^{-1}AP=\begin{pmatrix}1&0\\0&0,94\end{pmatrix}=D $ - Démontrer que pour tout entier naturel $n$ supérieur ou égal à $1$, $A^n = P D^n P^{- 1}$.
Montrons par récurrence sur $n$ que pour tout entier naturel $n$ non nul : $A^n = P \times D^n \times P^{- 1} $- Initialisation : $D=P^{- 1}\times A\times P$ (question précédente). d'où en multipliant à gauche par $P$ et à droite par $P^{- 1}$ , il vient :
$P \times D^1 \times P^{- 1}=P\times P^{- 1}\times A\times P\times P^{- 1} $ et donc n a bien $A^1 = P \times D^1 \times P^{- 1}$ - Hérédité : Supposons qu'il existe $k \geq 1$ tel que $A^k = P \times D^k \times P^{- 1}$. Alors $A^{k+1} = A^k \times A = \left(P \times D^k \times P^{- 1} \right) \times \left(P \times D \times P^{- 1} \right) =P \times D^k \times \left(P^{- 1} \times P \right) \times D \times P^{- 1} =$ $ P \times D^k \times I \times D \times P^{- 1} = P \times \left(D^k \times D \right)\times P^{- 1} =P \times D^{k+1}\times P^{- 1}$. La formule est donc vraie au rang $k + 1$. On a donc démontré par récurrence que pour tout entier naturel $n$ non nul : $A^n = P \times D^n \times P^{- 1}$.
- Initialisation : $D=P^{- 1}\times A\times P$ (question précédente). d'où en multipliant à gauche par $P$ et à droite par $P^{- 1}$ , il vient :
- Calculer $PQ$ et $QP$. En déduire la matrice $P^{-1}$ en fonction de $Q$. \\ $P\times Q= \begin{pmatrix}1&- 1\\5&1\end{pmatrix}\times \begin{pmatrix}1&1\\- 5&1\end{pmatrix}=\begin{pmatrix}6&0\\0&6\end{pmatrix}=6 Id_2$ $Q \times P = \begin{pmatrix}1&1\\- 5&1\end{pmatrix}\times \begin{pmatrix}1&- 1\\5&1\end{pmatrix}=\begin{pmatrix}6&0\\0&6\end{pmatrix}=6 Id_2$, donc $P$ est inversible et
- Les résultats des questions précédentes permettent d'établir que \[v_{n} = \dfrac{1}{6}\left(1 + 5 \times 0,94^n\right)v_{0} + \dfrac{1}{6}\left(1 - 0,94^n\right)c_{0}.\] Quelles informations peut-on en déduire pour la répartition de la population de cette région à long terme ?
Si $-1<q<1$ alors :$\lim\limits_{n \to +\infty}q^n=0$, donc $\lim\limits_{n \to +\infty}0,94^n=0$
$\left.\begin{array}{l} \lim\limits_{n \to +\infty}~\dfrac{1}{6}\left(1 + 5 \times 0,94^n\right)v_{0}= \dfrac{1}{6}v_0\\ \lim\limits_{n \to +\infty}~\dfrac{1}{6}\left(1 - 0,94^n\right)c_{0}=\dfrac{1}{6}c_0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{n \to +\infty}~v_{n}= \dfrac{1}{6}v_0+ \dfrac{1}{6}c_0=\dfrac{1}{6}\left (v_0+c_0\right )=\dfrac{250\;000}{6}\approx 41 667$
La population en ville sera, au bout d'un grand nombre d'années de 41 667 habitants, soit environ $\dfrac{1}{6}$ de la population totale .
- Vues: 45454
