Baccalauréat S Antilles-Guyane 11 septembre 2013

Exercice 1 4 points

Commun à tous les candidats

Partie A
Restitution organisée de connaissances
Soit $\Delta$ une droite de vecteur directeur $\vec{v}$ et soit P un plan. On considère deux droites sécantes et contenues dans P : la droite D$_{1}$ de vecteur directeur $\vec{u_{1}}$ et la droite D$_{2}$ de vecteur directeur $\vec{u_{2}}$. Montrer que $\Delta$ est orthogonale à toute droite de P si et seulement si $\Delta$ est orthogonale à D$_{1}$ et à D$_{2}$.

Partie B
Dans l'espace muni d'un repère orthonormé, on considère les trois points
\[\text{A}(0 ; - 1 ; 1),\quad \text{B}(4 ; -3 ; 0)\:\: \text{et}\:\: \text{C}(- 1 ; -2 ; -1).\] On appelle P le plan passant par A, B et C. On appelle $\Delta$ la droite ayant pour représentation paramétrique $\left\{\begin{array}{l c l} x &=& t\\y &=& 3t - 1\\z &=& -2t + 8 \end{array}\right.$ avec $t$ appartenant à $\mathbb{R}$. Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse.

1. Affirmation 1 : $\Delta$ est orthogonale à toute droite du plan P.
2. Affirmation 2 : les droites $\Delta$ et (AB) sont coplanaires.
3. Affirmation 3 : Le plan P a pour équation cartésienne $x + 3y - 2z + 5 = 0$.
4. On appelle D la droite passant par l'origine et de vecteur directeur $\vec{u}(11 ; - 1 ; 4)$.
   Affirmation 4 : La droite D est strictement parallèle au plan d'équation $x + 3y - 2z + 5 = 0$.

Exercice 1 4 points

Commun à tous les candidats

Partie A
Restitution organisée de connaissances
Soit $\Delta$ une droite de vecteur directeur $\vec{v}$ et soit P un plan. On considère deux droites sécantes et contenues dans P : la droite D$_{1}$ de vecteur directeur $\vec{u_{1}}$ et la droite D$_{2}$ de vecteur directeur $\vec{u_{2}}$. Montrer que $\Delta$ est orthogonale à toute droite de P si et seulement si $\Delta$ est orthogonale à D$_{1}$ et à D$_{2}$.

Partie B
Dans l'espace muni d'un repère orthonormé, on considère les trois points
\[\text{A}(0 ; - 1 ; 1),\quad \text{B}(4 ; -3 ; 0)\:\: \text{et}\:\: \text{C}(- 1 ; -2 ; -1).\] On appelle P le plan passant par A, B et C. On appelle $\Delta$ la droite ayant pour représentation paramétrique $\left\{\begin{array}{l c l} x &=& t\\y &=& 3t - 1\\z &=& -2t + 8 \end{array}\right.$ avec $t$ appartenant à $\mathbb{R}$. Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse.

Si $\Delta$ est orthogonale à toute droite de $P$ alors $\Delta$ est en particulier orthogonale à $D_1$ et à $D_2$.

Réciproquement, si $\Delta$ est orthogonale à $D_1$ et $D_2$, on a alors $\vec{u_1}.\vec{v} = 0$ et $\vec{u_2}.\vec{v} = 0$. Les $2$ droites $D_1$ et $D_2$ étant sécantes, les vecteurs $\vec{u_1}$ et $\vec{u_2}$ forment une base du plan $P$.

Soit $\vec{u}$ un vecteur directeur d’une droite $D$ de $P$. Il existe donc $2$ réels $a$ et $b$ tels que : $\vec{u}=a\vec{u_1}+b\vec{u2}$.

Par conséquent $\vec{u}.\vec{v} = a\vec{u_1}.\vec{v}+b\vec{u_2}.\vec{v} = 0$.

Les droites $D$ et $\Delta$ sont bien orthogonales.

1. Affirmation 1 : $\Delta$ est orthogonale à toute droite du plan P.
$\vec{AB}(4;-2;-1)$ et $\vec{AC}(-1;-1;-2)$. On constate que $\dfrac{4}{-1} \ne \dfrac{-2}{-1}$. Par conséquent ces $2$ vecteurs ne sont colinéaires et les droites $(AB)$ et $(AC)$ sont sécantes.
Un vecteur directeur de $\Delta$ est $\vec{v}(1;3;-2)$.
$\vec{v}.\vec{AB} = 1 \times 4 + 3 \times (-2) – 2 \times (-1) = 4 – 6 + 2 = 0$
$\vec{v}.\vec{AC} = 1 \times (-1) + 3 \times (-1) – 2 \times (-2) = -1 – 3 + 4 = 0$
La droite $\Delta$ est donc orthogonale à $2$ droites sécantes de $P$. Elle est, par conséquent, orthogonale à toute droite du plan $P$ d’après la propriété démontrée dans la partie A.
Affirmation vraie
2. Affirmation 2 : les droites $\Delta$ et (AB) sont coplanaires.
Une représentation paramétrique de $(AB)$ est : $\left\{ \begin{array}{l} x=4k \\\\y=-1-2k \qquad k\in\mathbb{R}\\\\z=1-k \end{array} \right.$.
Essayons de trouver un point commun à $(AB)$ et $\Delta$.
$\left\{ \begin{array}{l} t=4k \\\\3t-1=-1-2k \\\\-2t+8=1-k \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} t=4k \\\\12k-1=-1-2k \\\\-8k-8=1-k \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} t=4k \\\\k=0 \\\\k=1 \end{array} \right.$
Les $2$ droites sont orthogonales et n’ont pas de point commun. Elles ne sont donc pas coplanaires.
Affirmation fausse
3. Affirmation 3 : Le plan P a pour équation cartésienne $x + 3y - 2z + 5 = 0$.
$\vec{v}(1;3;-2)$ est normal au plan $P$. Une équation cartésienne de $P$ est donc de la forme : $x+3y-2z+d = 0$.
Le point $A\in P$. Donc $3 \times (-1) – 2 \times 1 + d = 0$ soit $d = 5$.
Affirmation vraie
4. On appelle D la droite passant par l'origine et de vecteur directeur $\vec{u}(11 ; - 1 ; 4)$.
   
   ffirmation 4 : La droite D est strictement parallèle au plan d'équation $x + 3y - 2z + 5 = 0$.
Regardons si $\vec{v}$ et $\vec{u}$ sont orthogonaux.
$\vec{v}.\vec{u} = 11 \times 1 – 1 \times 3 + 4 \times (-2) = 11 – 3 – 8 = 0$.
$D$ est donc parallèles au plan au plan $P$ ou contenue dans ce plan.
Or l’origine du repère n’appartient pas au plan $P$ (car $0 \ne 5$).
Affirmation fausse

Exercice 2 6 points

Commun à tous les candidats

Pour tout réel $k$ strictement positif, on désigne par $f_{k}$ la fonction définie et dérivable sur l'ensemble des nombres réels $\mathbb{R}$ telle que :
\[f_{k}(x) = kx\text{e}^{-kx}.\] On note $\mathcal{C}_{k}$ sa courbe représentative dans le plan muni d'un repère orthogonal $\left(\text{O}, \vec{i}, \vec{j}\right)$.
Partie A : Étude du cas $k = 1$
On considère donc la fonction $f_{1}$ définie sur $\mathbb{R}$ par
\[f_{1}(x) = x\text{e}^{- x}.\]

1. Déterminer les limites de la fonction $f_{1}$ en $- \infty$ et en $+ \infty$. En déduire que la courbe $\mathcal{C}_{1}$ admet une asymptote que l'on précisera.
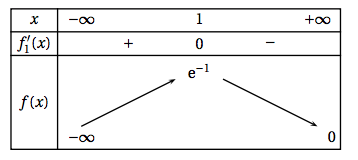
2. Étudier les variations de $f_{1}$ sur $\mathbb{R}$ puis dresser son tableau de variation sur $\mathbb{R}$.
3. Démontrer que la fonction $g_{1}$ définie et dérivable sur $\mathbb{R}$ telle que : \[g_{1}(x) = - (x + 1)\text{e}^{- x}\] est une primitive de la fonction $f_{1}$ sur $\mathbb{R}$.
4. Étudier le signe de $f_{1}(x)$ suivant les valeurs du nombre réel $x$.
5. Calculer, en unité d'aire, l'aire de la partie du plan délimitée par la courbe $\mathcal{C}_{1}$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = \ln 10$.

Partie B : Propriétés graphiques

On a représenté sur le graphique ci-dessous les courbes $\mathcal{C}_{2}$, $\mathcal{C}_{a}$ et $\mathcal{C}_{b}$ où $a$ et $b$ sont des réels strictement positifs fixés et T la tangente à $\mathcal{C}_{b}$ au point O origine du repère.

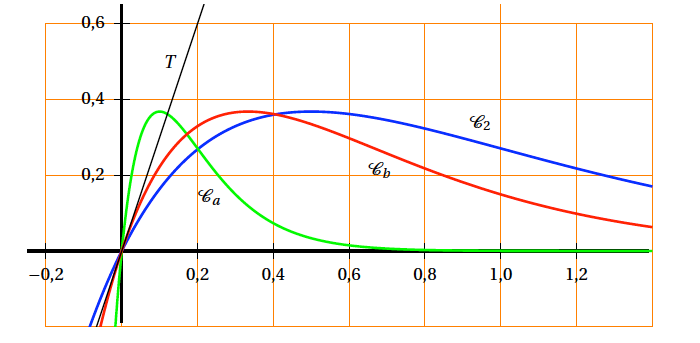
1. Montrer que pour tout réel $k$ strictement positif, les courbes $\mathcal{C}_{k}$ passent par un même point.
2. 1. Montrer que pour tout réel $k$ strictement positif et tout réel $x$ on a \[f'_{k}(x) = k(1 - kx)\text{e}^{- kx}.\]
   2. Justifier que, pour tout réel $k$ strictement positif, $f_{k}$ admet un maximum et calculer ce maximum.
   3. En observant le graphique ci-dessus, comparer $a$ et 2. Expliquer la démarche.
   4. Écrire une équation de la tangente à $\mathcal{C}_{k}$ au point O origine du repère.
   5. En déduire à l'aide du graphique une valeur approchée de $b$.

Exercice 2 6 points

Commun à tous les candidats

Pour tout réel $k$ strictement positif, on désigne par $f_{k}$ la fonction définie et dérivable sur l'ensemble des nombres réels $\mathbb{R}$ telle que :
\[f_{k}(x) = kx\text{e}^{-kx}.\] On note $\mathcal{C}_{k}$ sa courbe représentative dans le plan muni d'un repère orthogonal $\left(\text{O}, \vec{i}, \vec{j}\right)$.
Partie A : Étude du cas $k = 1$
On considère donc la fonction $f_{1}$ définie sur $\mathbb{R}$ par
\[f_{1}(x) = x\text{e}^{- x}.\]

1. Déterminer les limites de la fonction $f_{1}$ en $- \infty$ et en $+ \infty$. En déduire que la courbe $\mathcal{C}_{1}$ admet une asymptote que l'on précisera.
$\left.\begin{array}{l} \lim\limits_{x \to \1}~\2=\3\\ \lim\limits_{x \to \1}~\4=\5 \end{array}\right\}$ par \8 on obtient: $\lim\limits_{x \to \1}~\6=\7$ $f_1(x) = x\text{e}^{-x}=\dfrac{x}{\text{e}^{x}}$ D'après une limite usuelle , on a $\lim\limits_{x\rightarrow +\infty}\dfrac{\text{e}^{x}}{x} =+\infty$, donc par inverse on obtient : $\lim\limits_{x\rightarrow +\infty}\dfrac{x}{\text{e}^{x}} =0$
   Comme  $\lim\limits_{x\rightarrow +\infty}f_1(x) = 0$; la courbe $\mathcal{C}_1$ possède donc une asymptote horizontale d’équation $y=0$ au voisinage de $+\infty$.

2. Étudier les variations de $f_{1}$sur $\mathbb{R}$ puis dresser son tableau de variation sur $\mathbb{R}$.

$\1 $ est dérivable comme produit de deux fonctions dérivables : 

$\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
$$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

Ainsi :
 $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$


$$f_1'(x)=(1-x)\text{e}^{-x}$$
Comme la fonction exponentielle est strictement positive sur $\mathbb{R}$ ; le signe de $f_1′(x)$ ne dépend que de celui de $1-x$. On obtient donc le tableau de variations suivant :


3. Démontrer que la fonction $g_{1}$ définie et dérivable sur $\mathbb{R}$ telle que : \[g_{1}(x) = - (x + 1)\text{e}^{- x}\] est une primitive de la fonction $f_{1}$ sur $\mathbb{R}$.

$\1 $ est dérivable comme produit de deux fonctions dérivables : 

$\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
$$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

Ainsi :
 $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$


$$g_1'(x)=(-1+x+1)\text{e}^{-x}=x\text{e}^{-x}=f_1(x)$$
$g_1$ est donc bien une primitive de $f_1$ sur $\mathbb{R}$.
4. Étudier le signe de $f_{1}(x)$ suivant les valeurs du nombre réel $x$.
Comme la fonction exponentielle est strictement positive sur $\mathbb{R}$ ; $f_1(x)$ est du signe de $x$. Donc $f_1(x) < 0$ sur $]-\infty;0[$, $f_1(x) > 0$ sur $]0;+\infty[$ et $f_1(0)=0$.
5. Calculer, en unité d'aire, l'aire de la partie du plan délimitée par la courbe $\mathcal{C}_{1}$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = \ln 10$.
L'aire demandée correspond donc à :
$$\int_0^{\text{ln }10} f_1(x)\text{d}x = \left[-(x+1)\text{e}^{-x}\right]_0^{\text{ln } 10} = – \dfrac{\text{ln }(10) + 1}{10} + 1 = \dfrac{9 – \text{ln }(10)}{10} ~\text{u.a.}$$

Partie B : Propriétés graphiques

On a représenté sur le graphique ci-dessous les courbes $\mathcal{C}_{2}$, $\mathcal{C}_{a}$ et $\mathcal{C}_{b}$ où $a$ et $b$ sont des réels strictement positifs fixés et T la tangente à $\mathcal{C}_{b}$ au point O origine du repère.

1. Montrer que pour tout réel $k$ strictement positif, les courbes $\mathcal{C}_{k}$ passent par un même point.
$f_1(x) = kx\text{e}^{-kx}$ donc $f_k(0)=0$.
Par conséquent toutes les courbes $\mathcal{C}_k$ passent par l’origine du repère.
2. 1. Montrer que pour tout réel $k$ strictement positif et tout réel $x$ on a \[f'_{k}(x) = k(1 - kx)\text{e}^{- kx}.\]

   $\1 $ est dérivable comme produit de deux fonctions dérivables : 

   $\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
   $$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

   Ainsi :
    $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$

   
   $$f_k'(x)=k(1 - kx)\text{e}^{- kx}$$
   
   2. Justifier que, pour tout réel $k$ strictement positif, $f_{k}$ admet un maximum et calculer ce maximum.
   $f_k’(x)$ est donc du signe de $(1-kx)$.
   La fonction $f_k$ est par conséquent croissante sur $\left]-\infty;\dfrac{1}{k}\right]$ et croissante sur $\left[\dfrac{1}{k};+\infty\right[$.
   Elle admet donc un maximum en $\dfrac{1}{k}$ et $f_k\left(\dfrac{1}{k}\right)=\text{e}^{-1}$.
   
   3. En observant le graphique ci-dessus, comparer $a$ et 2. Expliquer la démarche.
   L’abscisse du sommet est $\dfrac{1}{k}$. Graphiquement, on constate que le sommet de $\mathcal{C}_a$ est situé, horizontalement, avant celui de $\mathcal{C}_2$.
   Par conséquent $a > 2$.
   
   4. Écrire une équation de la tangente à $\mathcal{C}_{k}$ au point O origine du repère.

   La tangente $\1$ à $\2$ au point d'abscisse $a= \3$ a pour équation : $$y=\6'(\3)(x-\3)+\6(\3)$$ Ici $a= \3$, on calcule successivement :

   • $\6\left(\3 \right)=\4$
   • $\6'\left (\3\right )=\5$

   Ainsi $\1:y=\5\left (x-\3\right )+\4$

   
   Une équation de la tangente en $O$ est donc $y= kx$.
   5. En déduire à l'aide du graphique une valeur approchée de $b$.
   On constate que le coefficient directeur de $T$ est environ $\dfrac{0,6}{0,2} = 3$. Donc $b=3$.

Exercice 3 4 points

Commun à tous les candidats

Une entreprise industrielle fabrique des pièces cylindriques en grande quantité. Pour toute pièce prélevée au hasard, on appelle $X$ la variable aléatoire qui lui associe sa longueur en millimètre et $Y$ la variable aléatoire qui lui associe son diamètre en millimètre. On suppose que $X$ suit la loi normale de moyenne $\mu_{1} = 36$ et d'écart-type $\sigma_{1} = 0,2$ et que $Y$ suit la loi normale de moyenne $\mu_{2} = 6$ et d'écart-type $\sigma_{2} = 0,05$.

1. Une pièce est dite conforme pour la longueur si sa longueur est comprise entre $\mu_{1} - 3\sigma_{1}$ et $\mu_{1} + 3\sigma_{1}$. Quelle est une valeur approchée à $10^{- 3}$ près de la probabilité $p_{1}$ pour qu'une pièce prélevée au hasard soit conforme pour la longueur ?


2. Une pièce est dite conforme pour le diamètre si son diamètre est compris entre 5,88 mm et 6,12 mm. Le tableau donné ci-contre a été obtenu à l'aide d'un tableur. Il indique pour chacune des valeurs de $k$, la probabilité que $Y$ soit inférieure ou égal à cette valeur. Déterminer à $10^{- 3}$ près la probabilité $p_{2}$ pour qu'une pièce prélevée au hasard soit conforme pour le diamètre (on pourra s'aider du tableau ci-contre). $$\begin{array}{|c|c|}\hline k & p(Y \leqslant k)\\ \hline 5,8 &3,16712 \text{E}-05\\ \hline 5,82 &0,000159109 \\ \hline 5,84 &0,000687138 \\ \hline 5,86 &0,00255513 \\ \hline 5,88 &0,008197536 \\ \hline 5,9 &0,022750132 \\ \hline 5,92 &0,054799292 \\ \hline 5,94 &0,11506967 \\ \hline 5,96 &0,211855399 \\ \hline 5,98 &0,344578258 \\ \hline 6 &0,5 \\ \hline 6,02 &0,655421742 \\ \hline 6,04 &0,788144601 \\ \hline 6,06 &0,88493033 \\ \hline 6,08 &0,945200708 \\ \hline 6,1 &0,977249868 \\ \hline 6,12 &0,991802464 \\ \hline 6,14 &0,99744487 \\ \hline 6,16 &0,999312862 \\ \hline 6,18 &0,999840891 \\ \hline 6,2 &0,999968329 \\ \hline \end{array}$$
3. On prélève une pièce au hasard. On appelle $L$ l'évènement «la pièce est conforme pour la longueur » et $D$ l'évènement «la pièce est conforme pour le diamètre ».
   On suppose que les évènements $L$ et $D$ sont indépendants.
   1. Une pièce est acceptée si elle est conforme pour la longueur et pour le diamètre. Déterminer la probabilité pour qu'une pièce prélevée au hasard ne soit pas acceptée (le résultat sera arrondi à $10^{-2}$).
   2. Justifier que la probabilité qu'elle soit conforme pour le diamètre sachant qu'elle n'est pas conforme pour la longueur, est égale à $p_{2}$.

Exercice 3 4 points

Commun à tous les candidats

Une entreprise industrielle fabrique des pièces cylindriques en grande quantité. Pour toute pièce prélevée au hasard, on appelle $X$ la variable aléatoire qui lui associe sa longueur en millimètre et $Y$ la variable aléatoire qui lui associe son diamètre en millimètre. On suppose que $X$ suit la loi normale de moyenne $\mu_{1} = 36$ et d'écart-type $\sigma_{1} = 0,2$ et que $Y$ suit la loi normale de moyenne $\mu_{2} = 6$ et d'écart-type $\sigma_{2} = 0,05$.

1. Une pièce est dite conforme pour la longueur si sa longueur est comprise entre $\mu_{1} - 3\sigma_{1}$ et $\mu_{1} + 3\sigma_{1}$. Quelle est une valeur approchée à $10^{- 3}$ près de la probabilité $p_{1}$ pour qu'une pièce prélevée au hasard soit conforme pour la longueur ?

On cherche donc la probabilité $P(µ1-3\sigma_1 \le X \le µ_1+3\sigma_1) \approx 0,997$ (formule du cours).
2. 
   Une pièce est dite conforme pour le diamètre si son diamètre est compris entre 5,88 mm et 6,12 mm.
   Le tableau donné ci-contre a été obtenu à l'aide d'un tableur. Il indique pour chacune des valeurs de $k$, la probabilité que $Y$ soit inférieure ou égal à cette valeur. Déterminer à $10^{- 3}$ près la probabilité $p_{2}$ pour qu'une pièce prélevée au hasard soit conforme pour le diamètre (on pourra s'aider du tableau ci-contre).} $$\begin{array}{|c|c|}\hline k & p(Y \leqslant k)\\ \hline 5,8 &3,16712 \text{E}-05\\ \hline 5,82 &0,000159109 \\ \hline 5,84 &0,000687138 \\ \hline 5,86 &0,00255513 \\ \hline 5,88 &0,008197536 \\ \hline 5,9 &0,022750132 \\ \hline 5,92 &0,054799292 \\ \hline 5,94 &0,11506967 \\ \hline 5,96 &0,211855399 \\ \hline 5,98 &0,344578258 \\ \hline 6 &0,5 \\ \hline 6,02 &0,655421742 \\ \hline 6,04 &0,788144601 \\ \hline 6,06 &0,88493033 \\ \hline 6,08 &0,945200708 \\ \hline 6,1 &0,977249868 \\ \hline 6,12 &0,991802464 \\ \hline 6,14 &0,99744487 \\ \hline 6,16 &0,999312862 \\ \hline 6,18 &0,999840891 \\ \hline 6,2 &0,999968329 \\ \hline \end{array}$$
On cherche donc $P(5,88 \le Y \le 6,12) = P(Y \le 6,12) – P(Y \le 5,88) \approx 0,984$.


2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

3. On prélève une pièce au hasard. On appelle $L$ l'évènement «la pièce est conforme pour la longueur » et $D$ l'évènement «la pièce est conforme pour le diamètre ».
   On suppose que les évènements $L$ et $D$ sont indépendants.
   1. Une pièce est acceptée si elle est conforme pour la longueur et pour le diamètre. Déterminer la probabilité pour qu'une pièce prélevée au hasard ne soit pas acceptée (le résultat sera arrondi à $10^{-2}$).
   On cherche donc $P(D \cap L) = P(D) \times P(L)$ car les$2$ événements sont indépendants.
   Par conséquent $p(D \cap L) = p_1 \times p_2 \approx 0,98 \text{ à } 10^{-2} \text{ près}$.
   La probabilité que la pièce ne soit pas acceptée est donc de $1-0,98 = 0,02$.
   
   2. Justifier que la probabilité qu'elle soit conforme pour le diamètre sachant qu'elle n'est pas conforme pour la longueur, est égale à $p_{2}$.
   $D$ et $L$ sont indépendants. Il en est donc de même pour $\bar{D}$ et $L$.
   Par conséquent $p_{\bar{D}}(L) = p(L) = p_2$.

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Les deux parties sont indépendantes.
Le robot Tom doit emprunter un pont sans garde-corps de 10 pas de long et de 2 pas de large. Sa démarche est très particulière :

• Soit il avance d'un pas tout droit ;
• Soit il se déplace en diagonale vers la gauche (déplacement équivalent à un pas vers la gauche et un pas tout droit) ;
• Soit il se déplace en diagonale vers la droite (déplacement équivalent à un pas vers la droite et un pas tout droit).

On suppose que ces trois types de déplacement sont aléatoires et équiprobables.
L'objectif de cet exercice est d'estimer la probabilité $p$ de l'évènement $S$ «Tom traverse le pont » c'est-à-dire «Tom n'est pas tombé dans l'eau et se trouve encore sur le pont au bout de 10 déplacements ».
Partie A : modélisation et simulation
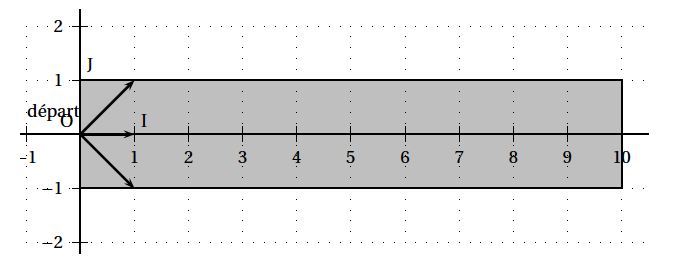
On schématise le pont par un rectangle dans le plan muni d'un repère orthonormé (O , I, J) comme l'indique la figure ci-dessous. On suppose que Tom se trouve au point de coordonnées (0 ; 0) au début de la traversée. On note $(x ; y)$ les coordonnées de la position de Tom après $x$ déplacements.
Figure

On a écrit l'algorithme suivant qui simule la position de Tom au bout de $x$ déplacements :

$$\begin{array}{|l|}\hline x, y, n \text{ sont des entiers}\\ \text{ Affecter à } x \text{ la valeur 0}\\ \text{ Affecter à } y \text{ la valeur 0}\\ \text{ Tant que } y \geqslant - 1 \text{ et } y \leqslant 1 \text{ et } x \leqslant 9\\ \hspace{1.5cm}\text{ Affecter à } n \text{ une valeur choisie au hasard entre - 1, 0 et 1}\\ \hspace{1.5cm}\text{ Affecter à } y \text{ la valeur } y + n\\ \hspace{1.5cm}\text{ Affecter à } x \text{ la valeur } x + 1 \\ \text{ Fin tant que } \\ \text{ Afficher } \ll \text{ la position de Tom est } (x\; ;\;y) \gg \\ \hline \end{array}$$

1. On donne les couples suivants : $(-1 ; 1)$ ; (10 ; 0); (2 ; 4) ; (10 ; 2). Lesquels ont pu être obtenus avec cet algorithme ? Justifier la réponse.
2. Modifier cet algorithme pour qu'à la place de «la position de Tom est $(x ; y)$ », il affiche finalement «Tom a réussi la traversée » ou «Tom est tombé ».

Partie B
Pour tout $n$ entier naturel compris entre 0 et 10, on note :
$A_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée $- 1$ ».
$B_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 0 ».
$C_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 1 ». On note $a_{n}, b_{n}, c_{n}$ les probabilités respectives des évènements $A_{n}, B_{n}, C_{n}$.

1. Justifier que $a_{0} = 0, b_{0} = 1, c_{0} = 0$.
2. Montrer que pour tout entier naturel $n$ compris entre $0$ et $9$, on a \[\left\{\begin{array}{l c l} a_{n+1} &=& \dfrac{a_{n} + b_{n}}{3}\\ b_{n+1} &=& \dfrac{a_{n} + b_{n} + c_{n}}{3} \end{array}\right.\]
   On pourra s'aider d'un arbre pondéré.
3. Calculer les probabilités $p\left(A_{1}\right),\: p\left(B_{1}\right)$ et $p\left(C_{1}\right)$.
4. Calculer la probabilité que Tom se trouve sur le pont au bout de deux déplacements.
5. À l'aide d'un tableur, on a obtenu la feuille de calcul ci-contre qui donne des valeurs approchées de $a_{n},\: b_{n},\: c_{n}$ pour $n$ compris entre 0 et 10. Donner une valeur approchée à $0,001$ près de la probabilité que Tom traverse le pont (on pourra s'aider du tableau ci-dessous). $$\begin{array}{|c|c|c|c|}\hline n &a_{n} &b_{n} &c_{n} \\ \hline 0 &0 &1 &0\\ \hline 1 &0,333333 &0,333333 &0,333333\\ \hline 2 &0,222222 &0,333333 &0,222222\\ \hline 3 &0,185185 &0,259259 &0,185185\\ \hline 4 &0,148148 &0,209877 &0,148148\\ \hline 5 &0,119342 &0,168724 &0,119342\\ \hline 6 &0,096022 &0,135802 &0,096022\\ \hline 7 &0,077275 &0,109282 &0,077275\\ \hline 8 &0,062186 &0,087944 &0,062186\\ \hline 9 &0,050043 &0,070772 &0,050043\\ \hline 10 &0,040272 &0,056953 &0,040272\\ \hline \end{array} $$

 

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Les deux parties sont indépendantes.
Le robot Tom doit emprunter un pont sans garde-corps de 10 pas de long et de 2 pas de large. Sa démarche est très particulière :

• Soit il avance d'un pas tout droit ;
• Soit il se déplace en diagonale vers la gauche (déplacement équivalent à un pas vers la gauche et un pas tout droit) ;
• Soit il se déplace en diagonale vers la droite (déplacement équivalent à un pas vers la droite et un pas tout droit).

On suppose que ces trois types de déplacement sont aléatoires et équiprobables.
L'objectif de cet exercice est d'estimer la probabilité $p$ de l'évènement $S$ «Tom traverse le pont » c'est-à-dire «Tom n'est pas tombé dans l'eau et se trouve encore sur le pont au bout de 10 déplacements ».
Partie A : modélisation et simulation
On schématise le pont par un rectangle dans le plan muni d'un repère orthonormé (O , I, J) comme l'indique la figure ci-dessous. On suppose que Tom se trouve au point de coordonnées (0 ; 0) au début de la traversée. On note $(x ; y)$ les coordonnées de la position de Tom après $x$ déplacements.
Figure

On a écrit l'algorithme suivant qui simule la position de Tom au bout de $x$ déplacements :

$$\begin{array}{|l|}\hline x, y, n \text{ sont des entiers}\\ \text{ Affecter à } x \text{ la valeur 0}\\ \text{ Affecter à } y \text{ la valeur 0}\\ \text{ Tant que } y \geqslant - 1 \text{ et } y \leqslant 1 \text{ et } x \leqslant 9\\ \hspace{1.5cm}\text{ Affecter à } n \text{ une valeur choisie au hasard entre - 1, 0 et 1}\\ \hspace{1.5cm}\text{ Affecter à } y \text{ la valeur } y + n\\ \hspace{1.5cm}\text{ Affecter à } x \text{ la valeur } x + 1 \\ \text{ Fin tant que } \\ \text{ Afficher } \ll \text{ la position de Tom est } (x\; ;\;y) \gg \\ \hline \end{array}$$

1. On donne les couples suivants : $(-1 ; 1)$ ; (10 ; 0); (2 ; 4) ; (10 ; 2). Lesquels ont pu être obtenus avec cet algorithme ? Justifier la réponse.
L’algorithme nous indique que nous sortons de la boucle quand $y < -1$,$y > 1$ ou $x>9$.
La variable $x$ est initialisée à $0$ et est augmentée de $1$ à chaque tour de boucle. Elle ne prend donc que des valeurs positives.
$(-1;1)$ ne peut donc pas être obtenu.
$(10;0)$ correspond au cas où toutes les valeurs de $y$ sont comprises entre $-1$ et $1$. On sort donc de la boucle du fait de la condition sur $x$. Ce couple peut être obtenu.
$(2;4)$ ne peut être obtenu car la plus grande valeur que peut prendre $y$ est $3$ (et on sort de la boucle à ce moment là!).
$(10;2)$ peut être obtenu en étant parti précédemment su couple $(9;1)$ et ayant choisi $1$ pour $n$.
2. Modifier cet algorithme pour qu'à la place de «la position de Tom est $(x ; y)$ », il affiche finalement «Tom a réussi la traversée » ou «Tom est tombé ».
Si $(y \ge -1 \text{ et } y \le 1)$
$\qquad$ alors Afficher « Tom a réussi la traversée ».
$\qquad$ sinon Afficher « Tom est tombé ».
Fin Si

Partie B
Pour tout $n$ entier naturel compris entre 0 et 10, on note :
$A_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée $- 1$ ».
$B_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 0 ».
$C_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 1 ». On note $a_{n}, b_{n}, c_{n}$ les probabilités respectives des évènements $A_{n}, B_{n}, C_{n}$.

1. Justifier que $a_{0} = 0, b_{0} = 1, c_{0} = 0$.
Quand $n = 0$, Tom est au point de coordonnées $(0;0)$.
Donc $a_0 = 0$, $b_0 = 1$ et $c_0 = 0$.
2. Montrer que pour tout entier naturel $n$ compris entre $0$ et $9$, on a \[\left\{\begin{array}{l c l} a_{n+1} &=& \dfrac{a_{n} + b_{n}}{3}\\ b_{n+1} &=& \dfrac{a_{n} + b_{n} + c_{n}}{3} \end{array}\right.\]
   On pourra s'aider d'un arbre pondéré.
Si Tom se trouve sur un point d’ordonnée $-1$ après $(n+1)$ déplacements, c’est qu’il vient soit d’un point d’ordonnée $0$ (c’est-à-dire $B_n$) ou d’ordonnée $-1$ (c’est-à-dire $A_n$).
Les trois types de déplacements sont équiprobables donc $a_{n+1} = \dfrac{a_n+b_n}{3}$.
Si Tom se trouve sur un point d’ordonnée $0$ après $(n+1)$ déplacements, c’est qu’il vient d’un point d’ordonnée $-1$ ($A_n$), d’ordonnée $0$ ($B_n$) ou d’ordonnée $1$ ($C_n$).
Les trois types de déplacements sont équiprobables donc $b_{n+1} = \dfrac{a_n+b_n+c_n}{3}$.
Pour la même raison que pour $a_{n+1}$, on a $c_{n+1} = \dfrac{c_n+b_n}{3}$.
3. Calculer les probabilités $p\left(A_{1}\right),\: p\left(B_{1}\right)$ et $p\left(C_{1}\right)$.
$p(A_1) = \dfrac{0+1}{3} = \dfrac{1}{3}$ et $p(B_1) = \dfrac{0 + 1 0}{3}=\dfrac{1}{3}$.
Au premier déplacement, Tom ne peut pas tomber donc $p(C_1) = 1 – p(A_1) – p(B_1) = \dfrac{1}{3}$.
4. Calculer la probabilité que Tom se trouve sur le pont au bout de deux déplacements.
$p(A_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{2}{9}$
$p(B_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{1}{3}$
$p(C_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{2}{9}$.
5. À l'aide d'un tableur, on a obtenu la feuille de calcul ci-contre qui donne des valeurs approchées de $a_{n},\: b_{n},\: c_{n}$ pour $n$ compris entre 0 et 10. Donner une valeur approchée à $0,001$ près de la probabilité que Tom traverse le pont (on pourra s'aider du tableau ci-dessous). $$\begin{array}{|c|c|c|c|}\hline n &a_{n} &b_{n} &c_{n} \\ \hline 0 &0 &1 &0\\ \hline 1 &0,333333 &0,333333 &0,333333\\ \hline 2 &0,222222 &0,333333 &0,222222\\ \hline 3 &0,185185 &0,259259 &0,185185\\ \hline 4 &0,148148 &0,209877 &0,148148\\ \hline 5 &0,119342 &0,168724 &0,119342\\ \hline 6 &0,096022 &0,135802 &0,096022\\ \hline 7 &0,077275 &0,109282 &0,077275\\ \hline 8 &0,062186 &0,087944 &0,062186\\ \hline 9 &0,050043 &0,070772 &0,050043\\ \hline 10 &0,040272 &0,056953 &0,040272\\ \hline \end{array} $$
Les trois événements $A_{10}$, $B_{10}$ et $C_{10}$ sont disjoints donc :
$$p(A_{10} \cup B_{10} \cup C_{10}) = a_{10}+b_{10}+c_{10} \approx 0,137$$

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Partie A
On considère l'algorithme suivant :
$$\begin{array}{|l|}\hline A \text{ et } X \text{sont des nombres entiers }\\ \text{ Saisir un entier positif } A\\ \text{ Affecter à } X \text{ la valeur de } A\\ \text{ Tant que } X \text{ supérieur ou égal à 26}\\ \hspace{1.25cm}\text{ Affecter à } X \text{ la valeur } X - 26\\ \text{ Fin du tant que }\\ \text{ Afficher } X\\ \hline \end{array}$$

1. Qu'affiche cet algorithme quand on saisit le nombre 3 ?
2. Qu'affiche cet algorithme quand on saisit le nombre 55 ?
3. Pour un nombre entier saisi quelconque, que représente le résultat fourni par cet algorithme?

Partie B
On veut coder un bloc de deux lettres selon la procédure suivante (détaillée en quatre étapes) :
Étape 1 : chaque lettre du bloc est remplacée par un entier en utilisant le tableau ci-dessous:
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline A &B &C &D &E &F &G &H &I &J &K &L &M\\\hline 0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\\hline \hline N &O &P &Q &R &S &T &U &V &W &X &Y &Z \\ \hline 13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25\\\hline \end{array}$$

On obtient une matrice colonne $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ où $x_{1}$ correspond à la première lettre du mot et $x_{2}$ correspond à la deuxième lettre du mot.

Étape 2 : $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ est transformé en $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ tel que
\[\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}3&1\\5&2\end{pmatrix}\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\]
La matrice $C = \begin{pmatrix}3&1\\5&2\end{pmatrix}$ est appelée la matrice de codage.

Étape 3 : $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ est transformé en $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ tel que \[\left\{\begin{array}{l c l c l c l l} z_{1}& \equiv& y_{1}\: (26)& \text{avec}\:\: 0 &\leqslant& z_{1}&\leqslant& 25\\ z_{2}& \equiv& y_{2}\: (26)& \text{avec}\:\: 0 &\leqslant& z_{2}&\leqslant& 25 \end{array}\right.\]
Étape 4 : $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ est transformé en un bloc de deux lettres en utilisant le tableau de correspondance donné dans l'étape 1.
\begin{array}{|l} \text{ Exemple } : \text{ RE } \to \begin{pmatrix}17\\4\end{pmatrix}\to \begin{pmatrix}55\\93\end{pmatrix} \to \begin{pmatrix}3\\15\end{pmatrix}\to \text{ DP }\\ \text{Le bloc RE est donc codé en DP}\\ \end{array} Justifier le passage de $\begin{pmatrix}17\\4\end{pmatrix}$ à $\begin{pmatrix}55\\93\end{pmatrix}$ puis à $\begin{pmatrix}3\\15\end{pmatrix}$.

1. Soient $x_{1},\:x_{2},\:x'_{1},\:x'_{2}$ quatre nombres entiers compris entre 0 et 25 tels que $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ et $\begin{pmatrix}x'_{1}\\x'_{2}\end{pmatrix}$ sont transformés lors du procédé de codage en $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$.
   1. Montrer que $\left\{\begin{array}{l c l} 3x_{1}+ x_{2} & \equiv& 3x'_{1} + x'_{2} \quad (26)\\ 5x_{1}+ 2x_{2}&\equiv&5x'_{1} + 2x'_{2} \quad (26). \end{array}\right.$
   2. En déduire que $x_{1} \equiv x'_{1}\quad (26)$ et $x_{2} \equiv x'_{2} \quad (26)$ puis que $x_{1} = x'_{1}$ et $x_{2} = x'_{2}$.
2. On souhaite trouver une méthode de décodage pour le bloc DP :
   1. Vérifier que la matrice $C' = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}$ est la matrice inverse de $C$.
   2. Calculer $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ tels que $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}\begin{pmatrix}3\\15\end{pmatrix}$.
   3. Calculer $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ tels que $\left\{\begin{array}{l c l} x_{1}&\equiv &y_{1}\quad (26)\:\: \text{avec}\:0 \leqslant x_{1} \leqslant 25\\ x_{2}&\equiv &y_{2}\quad (26)\:\: \text{avec}\:0 \leqslant x_{2} \leqslant 25\\ \end{array}\right.$
   4. Quel procédé général de décodage peut-on conjecturer ?
3. Dans cette question nous allons généraliser ce procédé de décodage. On considère un bloc de deux lettres et on appelle $z_{1}$ et $z_{2}$ les deux entiers compris entre 0 et 25 associés à ces lettres à l'étape 3. On cherche à trouver deux entiers $x_{1}$ et $x_{2}$ compris entre 0 et 25 qui donnent la matrice colonne $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ par les étapes 2 et 3 du procédé de codage. Soient $y'_{1}$ et $y'_{2}$ tels que $\begin{pmatrix}y'_{1}\\y_{2}\end{pmatrix} = C' \begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ où $C' = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}$.
   Soient $x_{1}$ et $x_{2}$, les nombres entiers tels que $\left\{\begin{array}{l c l} x_{1}&\equiv & y'_{1} \quad (26) \: \text{avec}\:0 \leqslant x_{1}\leqslant 25\\ x_{2}&\equiv &y'_{2} \quad (26) \: \text{avec}\:0 \leqslant x_{2}\leqslant 25 \end{array}\right.$
   Montrer que $\left\{\begin{array}{l c l} 3x_{1}+ x_{2} & \equiv& z_{1} \quad (26)\\ 5x_{1}+ 2x_{2}&\equiv&z_{2} \quad (26). \end{array}\right.$. Conclure.
4. Décoder QC.

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Partie A
On considère l'algorithme suivant :
$$\begin{array}{|l|}\hline A \text{ et } X \text{sont des nombres entiers }\\ \text{ Saisir un entier positif } A\\ \text{ Affecter à } X \text{ la valeur de } A\\ \text{ Tant que } X \text{ supérieur ou égal à 26}\\ \hspace{1.25cm}\text{ Affecter à } X \text{ la valeur } X - 26\\ \text{ Fin du tant que }\\ \text{ Afficher } X\\ \hline \end{array}$$

1. Qu'affiche cet algorithme quand on saisit le nombre 3 ?
Si on saisit le nombre $3$, l’algorithme affiche $3$.
2. Qu'affiche cet algorithme quand on saisit le nombre 55 ?
Si on saisit le nombre $55$ l’algorithme affiche $3$.
3. Pour un nombre entier saisi quelconque, que représente le résultat fourni par cet algorithme?
Cet algorithme fournit le reste de la division euclidienne de $A$ par $26$.

Partie B
On veut coder un bloc de deux lettres selon la procédure suivante (détaillée en quatre étapes) :
Étape 1 : chaque lettre du bloc est remplacée par un entier en utilisant le tableau ci-dessous:
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline A &B &C &D &E &F &G &H &I &J &K &L &M\\\hline 0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\\hline \hline N &O &P &Q &R &S &T &U &V &W &X &Y &Z \\ \hline 13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25\\\hline \end{array}$$

On obtient une matrice colonne $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ où $x_{1}$ correspond à la première lettre du mot et $x_{2}$ correspond à la deuxième lettre du mot.

Étape 2 : $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ est transformé en $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ tel que
\[\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}3&1\\5&2\end{pmatrix}\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}\]
La matrice $C = \begin{pmatrix}3&1\\5&2\end{pmatrix}$ est appelée la matrice de codage.

Étape 3 : $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ est transformé en $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ tel que \[\left\{\begin{array}{l c l c l c l l} z_{1}& \equiv& y_{1}\: (26)& \text{avec}\:\: 0 &\leqslant& z_{1}&\leqslant& 25\\ z_{2}& \equiv& y_{2}\: (26)& \text{avec}\:\: 0 &\leqslant& z_{2}&\leqslant& 25 \end{array}\right.\]
Étape 4 : $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ est transformé en un bloc de deux lettres en utilisant le tableau de correspondance donné dans l'étape 1.
\begin{array}{|l} \text{ Exemple } : \text{ RE } \to \begin{pmatrix}17\\4\end{pmatrix}\to \begin{pmatrix}55\\93\end{pmatrix} \to \begin{pmatrix}3\\15\end{pmatrix}\to \text{ DP }\\ \text{Le bloc RE est donc codé en DP}\\ \end{array} Justifier le passage de $\begin{pmatrix}17\\4\end{pmatrix}$ à $\begin{pmatrix}55\\93\end{pmatrix}$ puis à $\begin{pmatrix}3\\15\end{pmatrix}$.

• Étape 1 :$\text{ RE } \to \begin{pmatrix}17\\4\end{pmatrix}$ en utilisant le tableau
• Étape 2 :$\begin{pmatrix}17\\4\end{pmatrix}$ est transformé en $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ tel que
  \[\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}3&1\\5&2\end{pmatrix}\begin{pmatrix}17\\4\end{pmatrix}=\begin{pmatrix}3\times 17 + 1\times 4\\5\times 17 + 2\times 4\end{pmatrix}=\begin{pmatrix}55\\93\end{pmatrix}\]
• Étape 3 : \[\left\{\begin{array}{l c l c l c l l} 55& \equiv& 3\: (26)& \text{avec}\:\: 0 &\leqslant& 3&\leqslant& 25\\93& \equiv& 15\: (26)& \text{avec}\:\: 0 &\leqslant& 13&\leqslant& 25 \end{array}\right.\]
• Étape 4 :$ \begin{pmatrix}3\\15\end{pmatrix} \to \text{ DP } $ en utilisant le tableau
  On a donc bien : \begin{array}{|l}  \text{ RE } \to \begin{pmatrix}17\\4\end{pmatrix}\to \begin{pmatrix}55\\93\end{pmatrix} \to \begin{pmatrix}3\\15\end{pmatrix}\to \text{ DP }\\ \text{Le bloc RE est donc codé en DP}\\ \end{array}

1. Soient $x_{1},\:x_{2},\:x'_{1},\:x'_{2}$ quatre nombres entiers compris entre 0 et 25 tels que $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ et $\begin{pmatrix}x'_{1}\\x'_{2}\end{pmatrix}$ sont transformés lors du procédé de codage en $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$.
   1. Montrer que $\left\{\begin{array}{l c l} 3x_{1}+ x_{2} & \equiv& 3x'_{1} + x'_{2} \quad (26)\\ 5x_{1}+ 2x_{2}&\equiv&5x'_{1} + 2x'_{2} \quad (26). \end{array}\right.$
   On a donc $y_1 = 3x_1 + x_2$ et $y_2=5x_1+2x_2$ ainsi que $y’_1 = 3x’_1+x’_2$ et $y’_2=5x’_1+2x’_2$.
   Or $z_1 \equiv y_1~(26)$ et $z_1 \equiv y’_1~(26)$ par conséquent $y_1 \equiv y’_1 ~(26)$.
   D’où $3x_1+x_2 \equiv 3x’_1+x’_2 ~(26)$.
   De même $z_2 \equiv y_2 ~(26)$ et $z_2 \equiv y’_2 ~(26)$ par conséquent $y_2 \equiv y’_2 ~(26)$
   Et $5x_1+2x_2 \equiv 5x’_1 + 2x’_2 ~(26)$.
   
   2. En déduire que $x_{1} \equiv x'_{1}\quad (26)$ et $x_{2} \equiv x'_{2} \quad (26)$ puis que $x_{1} = x'_{1}$ et $x_{2} = x'_{2}$.
   On appelle $L_1$ la ligne $3x_1 + x_2 \equiv 3x’_1 + x’_2 ~(26)$ et $L_2$ la ligne $5x_1 + 2x_2 \equiv 5x’_1 + 2x’_2 ~(26)$.
   Alors $2l_1-L2$ donne $x_1 \equiv x’_1~(26)$ et $3L_2 – 5L_1$ donne $x_2 \equiv x’_2~(26)$.
   Les nombres $x_1$, $x_2$, $x’_1$ et $x’_2$ sont des entiers compris entre $0$ et $25$.
   Par conséquent ils sont égaux à leur reste dans la division euclidienne par $26$.
   Cela signifie donc que $x_1 = x’_1$ et $x_2 = x’_2$.
2. On souhaite trouver une méthode de décodage pour le bloc DP :
   1. Vérifier que la matrice $C' = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}$ est la matrice inverse de $C$.
   $C \times C’ = \left( \begin{matrix} 1&0\\\\0&1 \end{matrix} \right)$. Par conséquent $C’$ est bien la matrice inverse de la matrice $C$.
   
   2. Calculer $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ tels que $\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix} = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}\begin{pmatrix}3\\15\end{pmatrix}$.
   $\left( \begin{matrix} y_1 \\\\ y_2 \end{matrix} \right) = \left( \begin{matrix} 2 \times 3 – 1 \times 15 \\\\-5 \times 3 + 3 \times 15 \end{matrix} \right) = \left( \begin{matrix} -9 \\\\ 30 \end{matrix} \right)$
   
   3. Calculer $\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ tels que $\left\{\begin{array}{l c l} x_{1}&\equiv &y_{1}\quad (26)\:\: \text{avec}\:0 \leqslant x_{1} \leqslant 25\\ x_{2}&\equiv &y_{2}\quad (26)\:\: \text{avec}\:0 \leqslant x_{2} \leqslant 25\\ \end{array}\right.$
   Alors $-9 = -26 + 17$ donc $x_1 = 17$ et $30 = 26 + 4$ d’où $x_2 = 4$.
   
   4. Quel procédé général de décodage peut-on conjecturer ?
   On peut donc conjecturer que $\left\{\begin{array}{lr} x_1\equiv 2y_1 – y_2~(26) & \text{avec } 0 \le x_1 \le 25 \\\\x_2 \equiv -5y_1 + 3y_2~(26) & \text{avec } 0 \le x_2 \le 25 \end{array} \right.$
3. Dans cette question nous allons généraliser ce procédé de décodage. On considère un bloc de deux lettres et on appelle $z_{1}$ et $z_{2}$ les deux entiers compris entre 0 et 25 associés à ces lettres à l'étape 3. On cherche à trouver deux entiers $x_{1}$ et $x_{2}$ compris entre 0 et 25 qui donnent la matrice colonne $\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ par les étapes 2 et 3 du procédé de codage. Soient $y'_{1}$ et $y'_{2}$ tels que $\begin{pmatrix}y'_{1}\\y_{2}\end{pmatrix} = C' \begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$ où $C' = \begin{pmatrix}2&- 1\\- 5&3\end{pmatrix}$.
   Soient $x_{1}$ et $x_{2}$, les nombres entiers tels que $\left\{\begin{array}{l c l} x_{1}&\equiv & y'_{1} \quad (26) \: \text{avec}\:0 \leqslant x_{1}\leqslant 25\\ x_{2}&\equiv &y'_{2} \quad (26) \: \text{avec}\:0 \leqslant x_{2}\leqslant 25 \end{array}\right.$
   Montrer que $\left\{\begin{array}{l c l} 3x_{1}+ x_{2} & \equiv& z_{1} \quad (26)\\ 5x_{1}+ 2x_{2}&\equiv&z_{2} \quad (26). \end{array}\right.$. Conclure.
$3x_1+x_2 \equiv 6y_1 – 3y_2 – 5y_1 + 3y_2 \equiv y_1 \equiv z_1 ~(26)$
$5x_1+2x_2 \equiv 10y_1 – 5y_2 – 10y_1 + 6y_2 \equiv y_2 \equiv z_2 ~(26)$
Par conséquent $\left( \begin{matrix} x_1 \\\\ x_2 \end{matrix} \right)$ est bien le couple de nombres initial ayant permis d’obtenir $\left( \begin{matrix} y_1 \\\\ y_2 \end{matrix} \right)$ à l’aide du procédé de codage.
4. Décoder QC.
$QC \rightarrow \left( \begin{matrix} 16 \\\\ 2 \end{matrix} \right)$
Alors $y’_1 = 16 \times 2 – 1 \times 2 = 30$ et $y’_2 = -5 \times 16 + 3 \times 2 = -74$.
Par conséquent $x’_1 = 4$ et $x’_2 = 4$.
Le code $QC$ provenait donc de $EE$.