Baccalauréat S Liban 31 mai 2016
Page 1 sur 12
Exercice 1 4 points
On considère un solide ADECBF constitué de deux pyramides identiques ayant pour base commune le carré ABCD de centre I.
Une représentation en perspective de ce solide est donnée en annexe (à rendre avec la copie) .
Toutes les arêtes sont de longueur $1$. L'espace est rapporté au repère orthonormé $\left(\text{A};\vec{\text{AB}},\vec{\text{AD}},\vec{\text{AK}}\right)$.
-
- Montrer que IE $= \dfrac{\sqrt{2}}{2}$. En déduire les coordonnées des points I, E et F.
- Montrer que le vecteur $\vec{n}\begin{pmatrix}0\\- 2\\\sqrt{2}\end{pmatrix}$ est normal au plan (ABE).
- Déterminer une équation cartésienne du plan (ABE).
- On nomme M le milieu du segment [DF] et N celui du segment [AB].
- Démontrer que les plans (FDC) et (ABE) sont parallèles.
- Déterminer l'intersection des plans (EMN) et (FDC).
- Construire sur l' annexe (à rendre avec la copie) la section du solide ADECBF par le plan (EMN).
Annexe de l'exercice 1 ( A rendre avec la copie)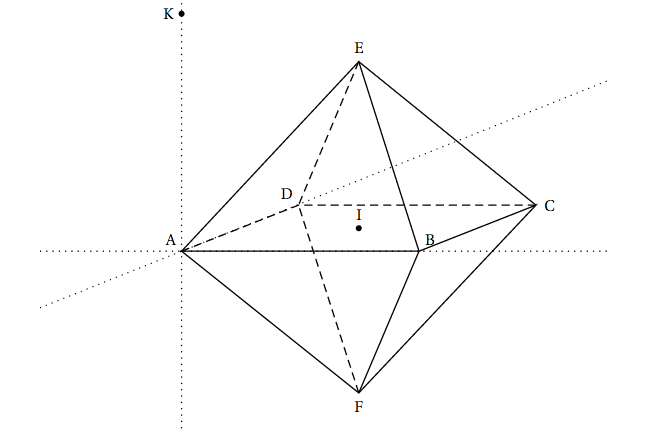
- Vues: 32205
