Baccalauréat S Asie 23 juin 2016

Page 1 sur 10

 

Exercice 1 5 points

Commun à tous les candidats

Un maraîcher est spécialisé dans la production de fraises. Cet exercice envisage dans la partie A la production de fraises, et dans la partie B leur conditionnement.
Les deux parties de cet exercice peuvent être traitées de façon indépendante.

Partie A: production de fraises

Le maraîcher produit ses fraises dans deux serres notées A et B ; 55% des fleurs de fraisier se trouvent dans la serre A, et 45% dans la serre B. Dans la serre A, la probabilité pour chaque fleur de donner un fruit est égale à 0,88 ; dans la serre B, elle est égale à 0,84.
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte.

• Proposition 1:
  La probabilité qu'une fleur de fraisier, choisie au hasard dans cette exploitation, donne un fruit est égale à 0,862.
• Proposition 2:
  On constate qu'une fleur, choisie au hasard dans cette exploitation, donne un fruit. La probabilité qu'elle soit située dans la serre A, arrondie au millième, est égale à 0,439.

Partie B: conditionnement des fraises

Les fraises sont conditionnées en barquettes. La masse (exprimée en gramme) d'une barquette peut être modélisée par une variable aléatoire $X$ qui suit la loi normale d'espérance $\mu=250$ et d'écart-type $\sigma$. La représentation graphique de la fonction densité de la loi de probabilité de la variable aléatoire $X$ est donnée ci-après: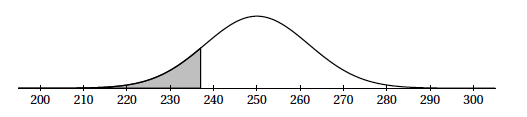

1. On donne $P(X \leqslant237)=0,14$. Calculer la probabilité de l'évènement « la masse de la barquette est comprise entre 237 et 263 grammes ».
2. On note $Y$ la variable aléatoire définie par: $Y=\dfrac{X-250}{\sigma}$.
   1. Quelle est la loi de la variable aléatoire $Y$?
   2. Démontrer que $P\left ( Y \leqslant- \dfrac{13}{\sigma}\right ) = 0,14$.
   3. En déduire la valeur de $\sigma$ arrondie à l'entier.
3. Dans cette question, on admet que $\sigma$ vaut 12. On désigne par $n$ et $m$ deux nombres entiers.
   1. Une barquette est conforme si sa masse, exprimée en gramme, se trouve dans l'intervalle $\texttt{[} 250-n~;~250+n \texttt{]}$. Déterminer la plus petite valeur de $n$ pour qu'une barquette soit conforme, avec une probabilité supérieure ou égale à 95%.
   2. On considère dans cette question qu'une barquette est conforme si sa masse, exprimée en gramme,se trouve dans l'intervalle $\texttt{[} 230~;~m\texttt{]}$. Déterminer la plus petite valeur de $m$ pour qu'une barquette soit conforme, avec une probabilité supérieure ou égale à 95%.