Baccalauréat S Métropole- La Réunion 12 septembre 2016

Page 1 sur 10

 

Exercice 1 6 points

Commun à tous les candidats

Les trois parties sont indépendantes. Les résultats des probabilités seront arrondis à $10^{-3} $ près.

Partie 1

On estime qu'en 2013 la population mondiale est composée de 4,6 milliards de personnes âgées de 20 à 79 ans et que 46,1 % des personnes âgées de 20 à 79 ans vivent en zone rurale et 53,9 % en zone urbaine. En 2013, d'après la fédération internationale du diabète, 9,9 % de la population mondiale âgée de 20 à 79 ans vivant en zone urbaine est atteinte de diabète et 6,4 % de la population mondiale âgée de 20 à 79 ans vivant en zone rurale est atteinte de diabète. On interroge au hasard une personne âgée de 20 à 79 ans. On note :

• $R$ l'évènement : «la personne choisie habite en zone rurale » ,
• $D$ l'évènement: «la personne choisie est atteinte de diabète » .

 

1. Traduire cette situation à l'aide d'un arbre de probabilité.
2. 1. Calculer la probabilité que la personne interrogée soit diabétique.
   2. La personne choisie est diabétique. Quelle est la probabilité qu'elle habite en zone rurale ?

 

Partie 2

Une personne est dite en hypoglycémie si sa glycémie à jeun est inférieure à 60 mg.dL$^{-1}$ et elle est en hyperglycémie si sa glycémie à jeun est supérieure à 110 mg. dL$^{-1}$. La glycémie à jeun est considérée comme «normale »  si elle est comprise entre 70 mg.dL$^{-1}$ et 110 mg.dL$^{-1}$. Les personnes ayant un taux de glycémie compris entre 60 et 70 mg.dL$^{-1}$ ne font pas l'objet d'un suivi particulier. On choisit au hasard un adulte dans cette population. Une étude a permis d'établir que la probabilité qu'il soit en hyperglycémie est 0,052 à $10^{-3}$ près. Dans la suite on admettra que cette probabilité est égale à $0,052$. On modélise la glycémie à jeun, exprimée en mg.dL$^{-1}$, d'un adulte d'une population donnée, par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu$ et d'écart-type $\sigma$. On donne ci-dessous la représentation graphique de la densité de probabilité de la variable aléatoire $X$.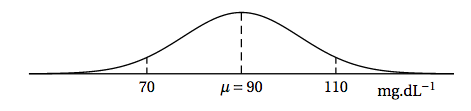

1. Quelle est la probabilité que la personne choisie ait une glycémie à jeun «normale»  ?
2. Déterminer la valeur de $\sigma$ arrondie au dixième.
3. Dans cette question, on prend $\sigma = 12$. Calculer la probabilité que la personne choisie soit en hypoglycémie.

 

Partie 3

Afin d'estimer la proportion, pour l'année 2013, de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans, on interroge au hasard 10000 personnes. Dans l'échantillon étudié, 716 personnes ont été diagnostiquées diabétiques.

1. À l'aide d'un intervalle de confiance au niveau de confiance 95 % , estimer la proportion de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans.
2. Quel doit être le nombre minimal de personnes à interroger si l'on veut obtenir un intervalle de confiance d'amplitude inférieure ou égale à 0,01 ?