Baccalauréat S Métropole- La Réunion 12 septembre 2016 - Spécialité
Page 9 sur 10
Spécialité 5 points
On dispose d'un dé équilibré à 6 faces numérotées de 1 à 6 et de 3 pièces A, B et C ayant chacune un côté pile et un côté face. Un jeu consiste à lancer une ou plusieurs fois le dé. Après chaque lancer de dé, si l'on obtient 1 ou 2, alors on retourne la pièce A, si l'on obtient 3 ou 4, alors on retourne la pièce B et si l'on obtient 5 ou 6, alors on retourne la pièce C. Au début du jeu, les 3 pièces sont toutes du côté face.
- Dans l'algorithme ci-dessous, 0 code le côté face et 1 code le côté pile. Si $a$ code un côté de la pièce A, alors $1 - a$ code l'autre côté de la pièce A. $$\begin{array}{|ll|}\hline \text{Variables :} &a, b, c, d, s\text{ sont des entiers naturels}\\ &i, n \text{ sont des entiers supérieurs ou égaux à } 1\\ \text{Initialisation :}&a \text{ prend la valeur }0\\ &b\text{ prend la valeur }0\\ &c \text{ prend la valeur }0\\ &\text{Saisir }n\\ \text{Traitement :} & \text{Pour }i \text{ allant de 1 à } n \text{ faire }\\ &\begin{array}{|l} d \text{ prend la valeur d'un entier aléatoire compris}\\ \text{entre 1 et }6\\ \text{ Si } d \leqslant 2\\ \hspace{0.5cm} \begin{array}{|l} \text{ alors } a \text{ prend la valeur } 1 - a\\ \text{ sinon Si } d \leqslant 4\\ \hspace{1.5cm}\begin{array}{|l} \text{ alors } b \text{ prend la valeur } 1 - b\\ \text{ sinon } c \text{ prend la valeur } 1 - c \end{array}\\ \hspace{1cm}\text{ FinSi }\\ \end{array}\\ \text{ FinSi }\\ s \text{ prend la valeur } a + b + c\\ \end{array}\\ &\text{ FinPour }\\ \text{Sortie :}&\text{ Afficher }s\\ \hline \end{array}$$
- On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 4 et 2. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme :
$$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&c&s\\ \hline \text{initialisation}&\text{X}&\text{X}& & & &\text{X}\\ \hline 1^{er}\text{ passage boucle Pour}& & & & & & \\ \hline 2^{ e}\text{ passage boucle Pour}& & & & & & \\ \hline 3^{ e}\text{ passage boucle Pour}& &&&&&\\ \hline \end{array}$$ - Cet algorithme permet-il de savoir si, après une exécution de $n$ tirages, les trois pièces sont du côté pile ?
- On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 4 et 2. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme :
- Pour tout entier naturel $n$, on note :
$\bullet~~$ $X_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté face »
$\bullet~~$ $Y_n$ l'évènement: « À l'issue de $n$ lancers de dés, une seule pièce est du côté pile et les autres sont du côté face»
$\bullet~~$ $Z_n$ l'évènement: « À l'issue de $n$ lancers de dés, exactement deux pièces sont du côté pile et l'autre est du côté face»
$\bullet~~$ $T_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté pile ».
De plus on note, $x_n = p\left(X_n\right)$ ; $y_n = p\left(Y_n\right)$ ; $z_n = p\left(Z_n\right)$ et $t_n = p\left(T_n\right)$ les probabilités respectives des évènements $X_n$, $Y_n$, $Z_n$ et $T_n$.- Donner les probabilités $x_0$ ,$y_0$, $z_0$ et $t_0$ respectives qu'au début du jeu il y ait 0, 1, 2 ou 3 pièces du côté pile.
- Recopier l'arbre ci-dessous et compléter les probabilités sur ses branches :
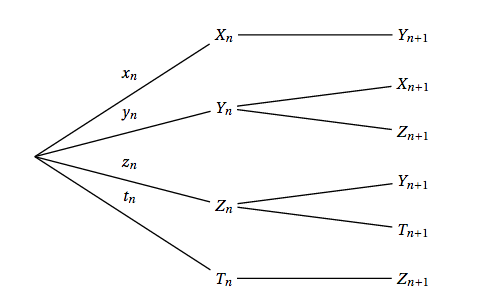
- Pour tout entier naturel $n$, on note $U_n$ la matrice ligne $\left(x_n y_n z_n t_n\right)$.
- Donner la matrice $U_0$.
- À l'aide de l'arbre précédemment rempli, déterminer la matrice carrée $M$ telle que, pour tout entier naturel $n$, $U_{n+1} = U_n \times M$.
- Démontrer que, pour tout entier naturel $n$, $U_n = U_0 \times M^n$.
- On admet que, pour tout entier $n \geqslant 1$,
$$\left\lbrace \begin{array}{l} x_n = \dfrac{(- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n + 3\times \left(\frac{1}{3}\right)^n + 1}{8}~\\ y_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n + 3 \times \left(\frac{1}{3}\right)^n - (- 1)^n \times 3 + 3}{8}\\ z_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n - 3 \times \left(\frac{1}{3}\right)^n + (- 1)^n\times 3 + 3}{8}\\ t_n = \dfrac{- (- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n - 3\times \left(\frac{1}{3}\right)^n + 1}{8} \end{array} \right. $$- Calculer la probabilité, arrondie à $10^{-3}$ près, qu'au bout de 5 lancers de dés, une seule des trois pièces soit du côté pile.
- Préciser si les affirmations suivantes sont vraies ou fausses. Une réponse non justifiée n'est pas prise en compte.
$\bullet~~$ Première affirmation : « À l'issue d'un nombre pair de lancers de dés, les pièces peuvent être toutes les trois du côté pile ».
$\bullet~~$ Deuxième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $\dfrac{1}{4}$ ».
$\bullet~~$ Troisième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $0,249$ ».
- Vues: 31262
