Baccalauréat S Asie 23 juin 2016 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Un catadioptre est un dispositif optique formé de trois miroirs en forme de « coin de cube», les faces réfléchissantes tournées vers l'intérieur. On en trouve dans les réflecteurs de certains véhicules ainsi que dans les appareils de topographie. Les points O, A, B et C sont des sommets d'un cube, de telle sorte que le repère $\left (\text{O}\,;\,\vec{\text{OA}},\,\vec{\text{OB}},\,\vec{\text{OC}} \right )$ soit un repère orthonormé. On utilisera ce repère dans tout l'exercice. Les trois miroirs du catadioptre sont représentés par les plans (OAB), (OBC) et (OAC). Les rayons lumineux sont modélisés par des droites.
Règles de réflexion d'un rayon lumineux (admises):

• lorsqu'un rayon lumineux de vecteur directeur $\vec{v}\,(a~;~b~;~c)$ est réfléchi par le plan (OAB), un vecteur directeur du rayon réfléchi est $\vec{v}\,(a~;~b~;~- c)$;
• lorsqu'un rayon lumineux de vecteur directeur $\vec{v}\,(a~;~b~;~c)$ est réfléchi par le plan (OBC), un vecteur directeur du rayon réfléchi est $\vec{v}\,(-a~;~b~;~c)$ ;
• lorsqu'un rayon lumineux de vecteur directeur $\vec{v}\,(a~;~b~;~c)$ est réfléchi par le plan (OAC), un vecteur directeur du rayon réfléchi est $\vec{v}\,(a~;~- b~;~c)$ ;
  
  

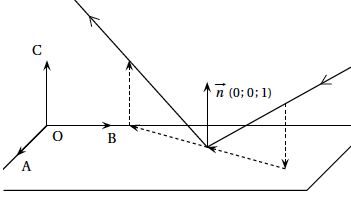
1. Propriété des catadioptres
   En utilisant les règles précédentes, démontrer que si un rayon lumineux de vecteur directeur $\vec{v}\,(a~;~b~;~c)$ est réfléchi successivement par les plans (OAB), (OBC) et (OAC), le rayon final est parallèle au rayon initial.
On considère un vecteur directeur $\vec{v}(a;b;c)$ d’un rayon.
Un vecteur directeur du rayon réfléchi par le plan $(OAB)$ est $\vec{v_1}(a;b-c)$.
Un vecteur directeur du rayon réfléchi ensuite par le plan $(OBC)$ est $\vec{v_2}(-a;b;-c)$.
Enfin un vecteur directeur du rayon réfléchi par le plan $(OAC)$ est $\vec{v_3}(-a;-b-;-c)$.
$\vec{v_3}=-\vec{v}$
Le rayon final est donc parallèle au rayon initial.
$\quad$

Pour la suite, on considère un rayon lumineux modélisé par une droite $d_1$ de vecteur directeur $\vec{v_1}\,(-2~;~-1~;~-1)$ qui vient frapper le plan (OAB) au point I$_1\,(2~;~3~;~0)$. Le rayon réfléchi est modélisé par la droite $d_2$ de vecteur directeur $\vec{v_2}\,(-2~;~-1~;~1)$ et passant par le point I$_1$.

2. Réflexion de $d_2$ sur le plan (OBC)
   
   1. Donner une représentation paramétrique de la droite $d_2$.
   Une représentation paramétrique de la droite $d_2$ est :
   $\begin{cases} x=2-2t\\y=3-t \quad t\in \mathbb R \\z=t \end{cases}$
   $\quad$
   
   2. Donner, sans justification, un vecteur normal au plan (OBC) et une équation cartésienne de ce plan.
   Un vecteur normal au plan $(OBC)$ est $\vec{OA}(1;0;0)$.
   Une équation cartésienne du plan $(OBC)$ est donc de la forme $x+d=0$.
   Puisque $O$ appartient à ce plan on a $d=0$ et par conséquent une équation cartésienne du plan $(OBC)$ est $x=0$.
   $\quad$
   
   3. Soit I$_2$ le point de coordonnées $(0~;~2~;~1)$.
      Vérifier que le plan (OBC) et la droite $d_2$ sont sécants en I$_2$.
   Si on prend $t=1$ dans la représentation paramétrique de $d_2$ on obtient $\begin{cases} x=0\\y=2\\z=1\end{cases}$. Donc le point $I_2$ appartient bien à $d_2$.
   L’abscisse de $I_2$ vaut $0$. $I_2$ appartient donc également au plan $(OBC)$.
   $\vec{OA}$ et $\vec{v_2}$ ne sont clairement pas colinéaires : la droite et le plan ne sont pas parallèles.
   Par conséquent la droite $d_2$ et le plan $(OBC)$ sont sécants en $I_2$.
   $\quad$
   On note $d_3$ la droite qui représente le rayon lumineux après réflexion sur le plan (OBC). $d_3$ est donc la droite de vecteur directeur $\vec{v_3}\,(2~;~-1~;~1)$ passant par le point I$_2\,(0~;~2~;~1)$.
3. Rélexion de $d_3$ sur le plan (OAC)
   Calculer les coordonnées du point d'intersection I$_3$ de la droite $d_3$ avec le plan (OAC). On note $d_4$ la droite qui représente le rayon lumineux après réflexion sur le plan (OAC). Elle est donc parallèle à la droite $d_1$.
Une équation cartésienne du plan $(OAC)$ est $y=0$.
Une représentation paramétrique de la droite $d_3$ est $\begin{cases} x=2t\\y=2-t \quad t \in \mathbb R \\z=1+t \end{cases}$
Le point d’intersection de ce plan et de cette droite est $I_3$.
Ses coordonnées vérifient à la fois les équations de la droite et celle du plan.
Donc $2-t=0$ soit $t=2$.
Par conséquent $\begin{cases} x=4\\y=0\\z=3 \end{cases}$
Finalement $I_3(4;0;3)$.
$\quad$
4. Etude du trajet de la lumière
   On donne le vecteur $\vec{u}\,(1~;~-2~;~0)$, et on note $\mathcal P$ le plan défini par les droites $d_1$ et $d_2$.
   1. Démontrer que le vecteur $\vec u$ est un vecteur normal au plan $\mathcal P$.
   $\vec{u}.\vec{v_1}=1\times (-2)+(-1)\times (-2)+0=0$
   $\vec{u}.\vec{v_2}=1\times (-2)+(-2)\times (-1)+0=0$
   Le vecteur $\vec{u}$ est donc orthogonal à deux vecteurs non colinéaires du plan $\mathscr{P}$.
   C’est par conséquent un vecteur normal à ce plan.
   $\quad$
   
   2. Les droites $d_1$, $d_2$ et $d_3$ sont-elles situées dans un même plan?
   Une équation cartésienne du plan $\mathscr{P}$ est donc de la forme $x-2y+d=0$.
   Le point $I_1(2;3,0)$ appartient à $\mathscr{P}$ car il appartient à $d_1$.
   Donc $2-6+d=0$ soit $d=4$.
   Une équation cartésienne de $\mathscr{P}$ est par conséquent $x-2y+4=0$.
   $\quad$
   Le point $I_3(4;0;3)$ appartient à $d_3$
   Mais $4-2\times 0+4\neq 0$. Le point $I_3$ n’appartient pas à $\mathscr{P}$.
   Les droites $d_1$, $d_2$ et $d_3$ ne sont pas situées dans un même plan.
   $\quad$
   
   3. Les droites $d_1$, $d_2$ et $d_4$ sont-elles situées dans un même plan?
   Le vecteur $\vec{v_1}$ est un vecteur directeur de la droite $d_4$. Le point $I_3$ appartient à cette droite.
   Le point $I_3$ n’appartient pas au plan $\mathscr{P}$ défini par les droites $d_1$ et $d_2$.
   Par conséquent les droites $d_1$, $d_2$ et $d_4$ ne sont pas situées dans un même plan.