Baccalauréat S Amérique du Sud 21 novembre 2017 - Correction Exercice 2
Page 4 sur 12
Correction de l'exercice 2 (4 points)
On considère un cube ABCDEFGH.
-
- Simplifier le vecteur $\vec{\text{AC}} + \vec{\text{AE}}$. $\vec{AC}+\vec{AE}=\vec{AC}+\vec{CG}=\vec{AG}$ d’après la relation de Chasles.
- En déduire que $\vec{\text{AG}}~\cdot~\vec{\text{BD}} = 0$. $\begin{align*} \vec{AG}.\vec{BD}&=\left(\vec{AC}+\vec{AE}\right).\vec{BD} \\
- On admet que $\vec{\text{AG}}~\cdot~\vec{\text{BE}} = 0$. Démontrer que la droite (AG) est orthogonale au plan (BDE). Le vecteur $\vec{AG}$ est othogonal à deux vecteurs non colinéaires du plan $(BDE)$. Il est donc orthogonal à ce plan.
$\quad$
&=\vec{AC}.\vec{BD}+\vec{AE}.\vec{BD} \\
&=0+0\\
&=0
\end{align*}$
$\vec{AC}.\vec{BD}=0$ car $[AC]$ et $[BD]$ sont les diagonales du carré $BCD$ (donc perpendiculaires entre-elles).
$\vec{AE}.\vec{BD}=0$ car $(AE)$ est orthogonale au plan $BCD$
$\quad$
Par conséquent la droite $(AG)$ est orthogonale au plan $(BDE)$.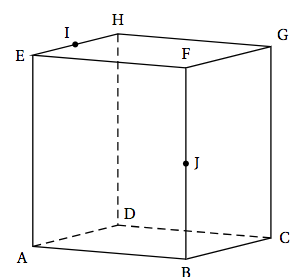
- L'espace est muni du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Démontrer qu'une équation cartésienne du plan (BDE) est $x + y + z - 1 = 0$. Dans le repère $\left(A;\vec{AB},\vec{AD},\vec{AE}\right)$ on a $A(0;0;0)$ et $G(1;1;1)$.
- Déterminer les coordonnées du point d'intersection K de la droite (AG) et du plan (BDE). Une représentation paramétrique de la droite $(AG)$ est $\begin{cases} x=k\\y=k\\z=k\end{cases}$ $\quad k\in \mathbb{R}$.
- On admet que l'aire, en unité d'aire, du triangle BDE est égale à $\dfrac{\sqrt{3}}{2}$. Calculer le volume de la pyramide BDEG. On a $KG=\sqrt{\left(1-\dfrac{1}{3}\right)^2+\left(1-\dfrac{1}{3}\right)^2+\left(1-\dfrac{1}{3}\right)^2}=\sqrt{\dfrac{12}{9}}=\dfrac{2\sqrt{3}}{3}$.
Par conséquent $\vec{AG}(1;1;1)$.
Une équation cartésienne du plan $(BDE)$ est donc de la forme $x+y+z+d=0$.
Le point $B(1;0;0)$ appartient à ce plan donc $1+0+0+d=0 \iff d=-1$.
Une équation cartésienne du plan $(BDE)$ est donc $x+y+z+z-1=0$.
$\quad$
Le point $K$ appartient à la fois à la droite $(AG)$ et au plan $(BDE)$.
Ses coordonnées sont donc solution du système :
$\begin{align*} \begin{cases} x=k\\y=k\\z=k\\x+y+z-1=0\end{cases} & \iff \begin{cases} x=k\\y=k\\z=k\\3k-1=0\end{cases} \\
&\iff \begin{cases} x=k\\y=k\\z=k\\k=\dfrac{1}{3}\end{cases}\\
&\iff \begin{cases} x=\dfrac{1}{3}\\y=\dfrac{1}{3}\\z=\dfrac{1}{3}\\k=\dfrac{1}{3}\end{cases}
\end{align*}$.
Donc $K\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3}\right)$.
$\quad$
Le volume de la pyramide $BDEG$ est :
$\begin{align*} V&=\dfrac{\text{aire}_{BDE}\times KG}{3}\\
&=\dfrac{\dfrac{\sqrt{3}}{2}\times \dfrac{2\sqrt{3}}{3}}{3} \\
&=\dfrac{1}{3}
\end{align*}$
$\quad$
- Vues: 77775
