Baccalauréat STI 2D/STL spécialité SPCL Métropole--La Réunion 7 septembre 2015 - Correction Exercice 3
Correction de l'exercice 3 (5 points)
" Avec une centaine de décès en moyenne par an, le monoxyde de carbone (CO) est la première cause de mortalité accidentelle par intoxication en France. Pourtant certains symptômes annonciateurs d'une intoxication au monoxyde de carbone existent. Maux de tête, nausées et vomissements sont notamment les premiers signes qui doivent alerter. Bien identifiés, ils permettent de réagir rapidement et d'éviter le pire."
Source Ministère des Affaires Sociales et de la Santé. (octobre 2012)
Document 1
La société COalerte fabrique un modèle de détecteurs qui enregistre en temps réel la concentration de monoxyde de carbone en parties par million (ppm). Un tel détecteur produit un signal d'alarme respectant les modalités fixées par la norme européenne EN 50 291 ci-dessous. Il déclenche un signal d'alarme :
- si la concentration est supérieure à 30 ppm pendant au moins 120 minutes ;
- si la concentration est supérieure à 50 ppm pendant au moins 60 minutes ;
- si la concentration est supérieure à 100 ppm pendant au moins la minutes ;
- si la concentration est supérieure à 300 ppm pendant au moins 3 minutes.
Document 2 
Un laboratoire d'essais procède à des tests sur un détecteur produit par la société COalerte en simulant un accident qui provoque une concentration anormale de monoxyde de carbone dans une pièce.
Partie A
Le laboratoire relève la concentration de monoxyde de carbone en fonction du temps, exprimé en heures. Les enregistrements effectués sur une période de 8 heures se traduisent par la représentation graphique ci-dessous.
- Estimer au bout de combien de temps devrait retentir un signal d'alarme. Par lecture graphique, on constate que la condition «la concentration est supérieure à 50 ppm pendant au moins 60 minutes» est la premiére a être réalisée d'où :
- Une personne présente dans la pièce depuis le début d'un tel accident risquerait-elle de présenter des symptômes? Si oui, lesquels? La concentration de monoxyde de carbone dépasse 20 ppm et est inférieure à 80 ppm d'après le document 2 :
avec la précision permise par le graphique, un signal d'alarme devrait retentir au bout de 80 minutes.
Une personne présente dans la pièce depuis le début d'un tel accident risque de présenter les symptômes suivants : «Troubles du rythme cardiaque ressentis chez les personnes les plus sensibles, souffrant de coronaropathie» et «Céphalées et nausées chez les enfants».
Partie B
Dans cette partie, tous les résultats seront arrondis à $10^{-2}$ près.
La concentration de monoxyde de carbone exprimée en ppm dans la pièce en fonction du temps, exprimé en heures, est modélisée par la fonction $f$ définie sur $[0~;~8]$ par \[f(t) = 2,2 + 200t\text{e}^{-t}.\]
- Calculer la concentration de monoxyde de carbone en ppm dans la pièce:
- au moment de l'accident; $f(0)=2,2$ par conséquent, au moment de l'accident, la concentration de monoxyde de carbone en ppm dans la pièce est de 2,2 ppm.
- 30 minutes après. $$f(0,5)=2,2+200\times0,5\times \text{e}^{-0,5}=2,2+100\times \text{e}^{-0,5}\approx 62,85$$ Une demi-heure après le début de l'accident, la concentration de monoxyde de carbone en ppm dans la pièce est de 62,85 ppm.
- À l'aide du graphique de la partie A, conjecturer les variations de la concentration de monoxyde de carbone dans la pièce en fonction du temps. Par lecture graphique,on obtient :
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0~;~8]$.
- Montrer que pour tout réel $t$ de l'intervalle $[0~;~8]$, $f'(t) = 200(1 - t)\text{e}^{-t}$. $f$ est dérivable comme somme de deux fonctions dérivables. $f=u v + 2,2$ d'où $f'=u'v+v'u $ avec pour tout réel $t$, dans $[0; 8]$ : $\left\{ \begin{array}{l} u(t)~ =200 t\\ v(t)~ =\text{e}^{-t} \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(t)~ =200 \\ v'(t)~ =-\text{e}^{-t} \end{array}\right.$ $$ \begin{array}{cl} f'(t)&=200\text{e}^{-t}+ \left (-\text{e}^{-t}\right )\times 200 t \\ & =200\text{e}^{-t}(1-t) \\ &=200(1 - t)\text{e}^{-t} \end{array} $$
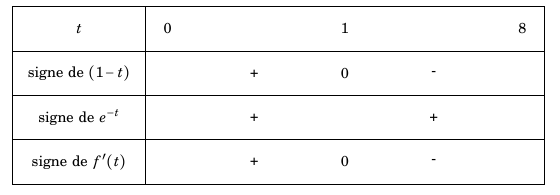
- Étudier le signe de $f'(t)$ sur l'intervalle $[0~;~8]$. Comme pour tout réel $t, e^{-t}>0$ alors, $f′(t)$ est du même signe que $1-t$ sur l'intervalle $[0;8]$. Or $$1-t\geq 0 0\iff -t\geq -1\iff t \leq 1$$ D'où le tableau du signe de $f′(t)$:
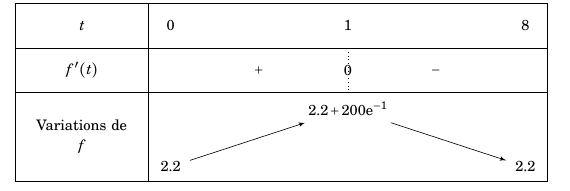
- Valider ou invalider la conjecture émise à la question 2. Les variations de la fonction $f$ se déduisent du signe de sa dérivée. D'où le tableau de variation de la fonction :
- On note $F$ la fonction définie sur l'intervalle $[0~;~8]$ par \[F(t) = 2,2 t - 200(t + 1)\text{e}^{-t}.\] On admet que $F$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~8]$.
- On rappelle que la valeur moyenne d'une fonction continue sur un intervalle $[a~;b]$ est le nombre réel défini par : $\dfrac{1}{b-a} \displaystyle\int_a^b f(t)\:\text{d}t$. Calculer la valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident. $$\begin{array}{rl} \dfrac{1}{8-0}\displaystyle\int_0^8f(t)\;\text{d}t & = \dfrac{1}{8-0}\left [F(8)-F(0)\right] \\ & \dfrac{1}{8-0}\left [(2,2\times 8-200\times 9\times e^{-8})-(2,2\times 0-200\times 9\times e^{0})\right] \\ &\dfrac{1}{8-0}\left [(17,6-1800\times e^{-8})+1800\right]\\ &= 27,2-225\times e^{-8} \\ &\approx 27,12 \end{array}$$
- Pour des raisons de sécurité, le ministère du travail fixe un seuil pour la concentration moyenne de monoxyde de carbone. Ce seuil est de $50$~ppm pour une période de 8 heures. La sécurité des personnes présentes dans la pièce aurait-elle été remise en cause lors de l'accident simulé ?
La valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident est d'environ 27,12 ppm.La valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident est inférieure à 50 ppm par conséquent, la sécurité des personnes présentes dans la pièce n'a pas été remise en cause lors de l'accident simulé.
$f$ est croissante sur $[0;1]$.
$f$ est décroissante sur $[1;8]$.
- Vues: 22327
