Bac STI2D Polynésie 9 juin 2016 - Correction de l' Exercice 1

Page 2 sur 8: Correction de l' Exercice 1

Exercice 1 3 points

QCM

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte $1$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point. Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.
Dans cet exercice, $\text{i}$ désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$.

1. L'écriture exponentielle du nombre complexe $z = \dfrac{-3\text{i}}{1 + \text{i}}$ est :
   \[ \textbf{a.} z = \frac{3\sqrt{2}}{2}\text{e}^{-\text{i}\frac{5\pi}{4}}\hspace{2cm}\textbf{b.}z = - \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}}\hspace{2cm} \textbf{c.} z =\frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}} \hspace{2cm} \textbf{d.} z = \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{\pi}{4}} \]
Bonne réponse : c

 

On met tout d'abord $z$ sous forme algégrique $z = \dfrac{-3\text{i}}{1 + \text{i}}$ sous forme algébrique : \begin{align*} z &= \dfrac{-3\text{i}}{1 + \text{i}}\\ &= \dfrac{-3\text{i}(1 - \text{i})}{(1 + \text{i})(1 - \text{i})}\\ &=\dfrac{-3\text{i} +3\text{i}^2 }{(1^2 + 1^2)} \\ &=\dfrac{-3-3\text{i} }{2} \end{align*} $z=a+\text{i}b$ où $a= -\dfrac{3}{2}$ et $b= -\dfrac{3}{2}$
• Module : \begin{align*} |z| &= \sqrt{\left (\dfrac{3}{2}\right )^2+\left (\dfrac{3}{2}\right )^2}\\ &= \sqrt{ \dfrac{9}{4} +\dfrac{9}{4}}\\ &=\sqrt{ \dfrac{18}{4} } \\ &= \dfrac{3\sqrt{2}}{2} \end{align*}
• Argument :
  $$\left\lbrace \begin{array}{l} \cos \theta=\dfrac{a}{r}=\dfrac{-\dfrac{3}{2}}{\dfrac{3\sqrt{2}}{2}}= -\dfrac{3}{2}\times \dfrac{2}{3\sqrt 2}=-\dfrac{\sqrt 2}{2}\\ \sin \theta=\dfrac{b}{r}=\dfrac{-\dfrac{3}{2}}{\dfrac{3\sqrt{2}}{2}}= -\dfrac{3}{2}\times \dfrac{2}{3\sqrt 2}=-\dfrac{\sqrt 2}{2} \end{array} \right.$$ Donc $\theta = -\dfrac{3\pi}{4}$ convient ou en ajoutant $2\pi$,$\theta = -\dfrac{3\pi}{4}+2\pi= \dfrac{5\pi}{4}$
On déduit donc \begin{align*} z &=\left [\dfrac{3\sqrt 2}{2} ;\dfrac{5\pi}{4} \right ] \\ &= \dfrac{3\sqrt 2}{2}\left (\cos\left (\dfrac{5\pi}{4}\right )+\text{i} \sin\left (\dfrac{5\pi}{4}\right )\right ) \\ &= \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}} \end{align*}
• On utilise la calculatrice :( en mode degré) pour les vieilles TI83 ...
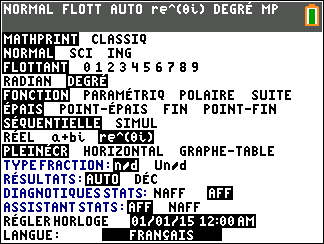
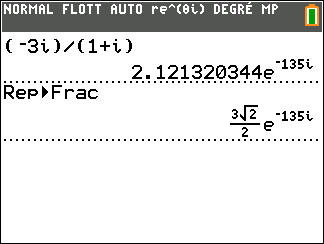
• On utilise la calculatrice :( en mode radian) pour la TI83 Premium ...
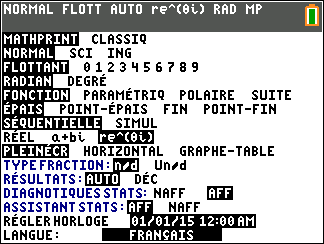
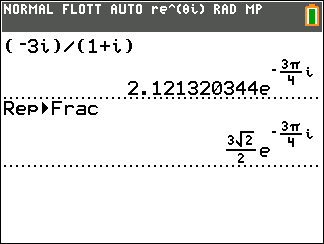
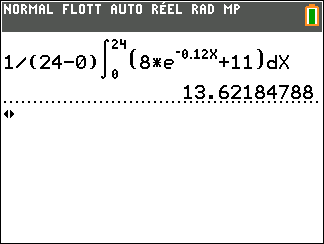
1. Soit $f$ la fonction définie pour tout réel $t$ positif par : $f(t) = 8\text{e}^{-0,12t  }+11$. La valeur moyenne de $f$ arrondie à $10^{-1}$ sur l'intervalle [0;24] est :
   $$ \textbf{a. }15,2\hspace{2cm} \textbf{b. }13,6 \hspace{2cm} \textbf{c }16,7 \hspace{2cm}\textbf{d. } 11,2$$
Bonne réponse : b

 

Une méthode rapide ? On utilise la calculatrice :

Le calcul direct : la valeur moyenne d'une fonction $f$ sur $[ a; b]$ est $V_{Moy}= \dfrac{1}{b-a}\displaystyle\int_a^b \; f(t)\; dt$

 

Ici $f(t)= 8\text{e}^{-0,12t  }+11$, une primitive est donc la fonction $F$ dénie sur $\mathbb R$ par $F(t) = \dfrac{8}{-0,12}\text{e}^{-0,12t  }+11t$ \begin{align*} V_{Moy} &= \dfrac{1}{24}\displaystyle\int_0^{24} \; f(t)\; dt \\ &= \dfrac{1}{24}\left (F(24)-F(0)\right )\\ F(24)&= \dfrac{8}{-0,12}\text{e}^{-0,12\times 24 }+11\times 24\approx 260,26 \\ F(0)&= \dfrac{8}{-0,12}\text{e}^{ 0}+11\times 0\approx -66.6 7 \\ V_{Moy} &\approx \dfrac{1}{24} (326.92)\approx 13,6 \end{align*}
1. On donne dans un repère orthonormé les points : A(0;2) ; B(1;3) ; C$(-2;1)$ et D$(-1;0)$. Le produit scalaire $\vec{\text{AB}} \cdot \vec{\text{CD}}$ est égal à :
   $$ \textbf{a.} \vec{\text{AB}} \cdot \vec{\text{CD}} = 0 \hspace{2cm}\hspace{2cm}\hspace{2cm} \textbf{b.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{0} \hspace{2cm}\hspace{2cm} \textbf{c.} \vec{\text{AB}} \cdot \vec{\text{CD}} = - 2 \hspace{2cm} \textbf{d.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{\text{AD}}$$
Bonne réponse : a

 

On a $\vec{AB} \begin{pmatrix} x_B-x_A \\y_B-y_A \end{pmatrix}= \begin{pmatrix} 1-0 \\3-2 \end{pmatrix}= \begin{pmatrix} 1 \\1 \end{pmatrix}$ de même on obtient $\vec{CD} \begin{pmatrix} 1 \\-1 \end{pmatrix}$ \begin{align*} \vec{\text{AB}} \cdot \vec{\text{CD}} &= XX'+YY'\\ &= 1\times 1 + (-1)\times 1\\ &= 1-1 \\ &=0 \end{align*}