Bac STI2D Polynésie 9 juin 2016 - Correction Exercice 2
Page 4 sur 8
Exercice 2 6 points
L'énergie photovoltaïque voit son coût baisser de façon importante depuis plusieurs années, ce qui engendre une croissance forte de ce secteur. L'évolution de la puissance solaire photovoltaïque installée dans le monde entre fin 2004 et fin 2015 est résumée dans le graphique ci-dessous : 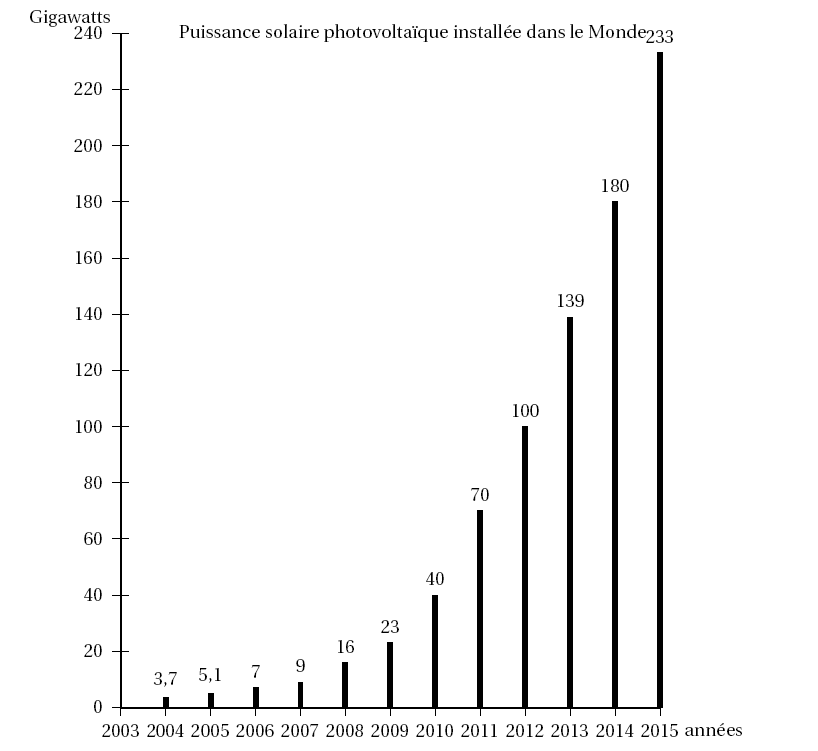
- Calculer les pourcentages d'augmentation annuels entre 2013 et 2014 ainsi qu'entre 2014 et 2015 $\left(\text{arrondir à } 10^{-1}\right)$. $\dfrac{180}{139} \approx 1,295 $ et $\dfrac{233}{180}\approx 1,294$.
- Calculer $P_1$ puis $P_2$ $\left(\text{arrondir à } 10^{-1}\right)$. On calcule $P_1= P_0 + 30\%\times P_0 = 233\times \left(1+\dfrac{30}{100}\right)= 1,3 \times 233 = 302,9$
- Exprimer $P_{n+1}$ en fonction de $P_n$. $\begin{align*} P_{n+1}&= P_n + 30\%\times P_n\\ & = \left(1+\dfrac{30}{100}\right)\times P_n\\ &= 1,3P_n \end{align*}$
- En déduire la nature de la suite $\left(P_n\right)$ et donner ses éléments caractéristiques. Ayant pour tout entier naturel $n$ ; $P_{n+1}=1,3P_n$, on déduit que la suite $\left(P_n\right)$ est géométrique de raison 1,3.
- Exprimer $P_n$ en fonction de $n$. Comme la suite $\left(P_n\right)$ est géométrique, on a $P_n=q^n \times P_0$ $$P_n=1,3^n \times 233$$
- Calculer la puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 (arrondir à l'unité). La puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 est donnée par $P_{10}=1,3^{10}\times 233\approx 3212$
- Quel est le pourcentage global d'augmentation de cette puissance solaire mondiale entre 2015 et 2025 (arrondir à l'unité) ? On calcule $t$ tel que $P_{10}=(1+t)P_0$ donc $1+t = \dfrac{P_{10}}{P_0}\approx \dfrac{3212}{233}\approx 13,7854$
- On veut déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde atteindrait 16000 GW. Pour atteindre cette puissance, les panneaux photovoltaïques occuperaient au sol l'équivalent d'un carré de 400km de côté et suffiraient pour produire toute l'électricité consommée dans le monde (consommation domestique, industrielle et des transports).
- On considère l'algorithme ci-dessous. Recopier et compléter les lignes 3 et 7 afin que cet algorithme réponde à la question posée. $$ \begin{array}{|l |l|}\hline 1/& \text{ Affecter à } N \text{ la valeur } 0 \\ 2/& \text{ Affecter à } P \text{ la valeur } 233\\ 3/& \text{ Tant que } \ldots\\ 4/&\text{ Affecter à } N \text{ la valeur } N +1 \\ 5/&\text{ Affecter à } P \text{ la valeur } P \times 1,30 \\ 6/&\text{ Fin Tant que }\\ 7/& \text{ Afficher } \ldots\\ \hline \end{array} $$ $$ \begin{array}{|l |l|}\hline 1/& \text{ Affecter à } N \text{ la valeur } 0 \\ 2/& \text{ Affecter à } P \text{ la valeur } 233\\ 3/& \text{ Tant que } P< 16\; 000\\ 4/&\text{ Affecter à } N \text{ la valeur } N +1 \\ 5/&\text{ Affecter à } P \text{ la valeur } P \times 1,30 \\ 6/&\text{ Fin Tant que }\\ 7/& \text{ Afficher } 2015+N\\ \hline \end{array} $$
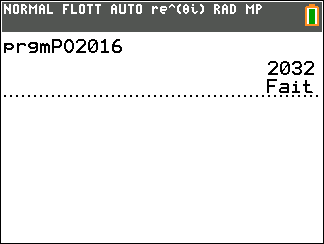
- En faisant tourner cet algorithme complété, déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde dépasserait 16000 GW. On utilise la calculatrice :
- Proposer une autre méthode, directe et non algorithmique, pour répondre à la question précédente en détaillant la démarche utilisée. $$\begin{array}{ll} P_n> 16 000 &\iff 1,3^n \times 233 > 16 000\\ &\iff 1,3^n > \dfrac{16 000}{233}\\ &\iff n \ln(1,3) > \ln \left(\dfrac{16 000}{233}\right)\\ &\iff n > \dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} \\ \end{array}$$ REMARQUE : Comme $\dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} \approx 16,12$, le plus petit entier $N$ tel que $N>\dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} $ est $N=17$. On retrouve le résultat de la question précédente.
Conclusion : La puissance solaire photovoltaïque installée dans le monde dépasserait 16000 GW pour la première fois en 2032.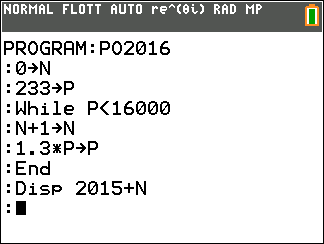
La puissance solaire photovoltaïque a augmenté de 29,5 % entre 2013 et 2014 et de 29,4 % entre 2014 et 2015.
On se propose d'estimer la puissance solaire photovoltaïque installée dans le monde dans les 15 ans à venir, si le taux de croissance annuel reste constant et égal à 30%. On note $P_n$ la puissance solaire photovoltaïque installée dans le monde, en GW, à la fin de l'année $2015 + n$. On a ainsi $P_0 = 233$.
$P_2= P_1 + 30\%\times P_1 = 302,9\times \left(1+\dfrac{30}{100}\right)= 1,3 \times 302,9 \approx 393,8$
La puissance solaire photovoltaïque installée dans le monde, sera de 302,9 GW, à la fin de l'année $2016$, et d'environ 393,8 GW, à la fin de l'année $2016$ .
La puissance solaire photovoltaïque installée dans le monde, sera d'environ 3212 GW, à la fin de l'année $2025$ .
On déduit $t\approx 12,79$
Lle pourcentage global d'augmentation de cette puissance solaire mondiale entre 2015 et 2025 est donc d'environ 1279%.
Exercice 3
- Vues: 20770
